Пусть на вход “1” поступает сигнал вида U₁=cos(₀t+4+₀), и может принимать значения “0” или “1”. Тогда сигнал на выходе умножителя U₂=cos(2₀t+2₀), следовательно, сигнал на выходе делителя U₃=cos(₀t+₀). Но все схемы опорного сигнала таковы, что в следствии различных неконтролируемых фактов возможны случайные изменения знака опорного сигнала. После этого может возникнуть явление “обратной работы”, в следствии которого внедрение системы с двоичной фазой модуляции оказалось невозможным.
3.3. Принятие решения приемником по одному отсчету
Сообщения передаются последовательностью двоичных символов "1" и "0", которые появляются с априорными вероятностями соответственно p(1)=0,27 и p(0)=0,73.
Этим символам соответствуют канальные сигналы S₁(t) и S₂(t), которые точно известны в месте приема.

В канале связи на передаваемые сигналы воздействует Гауссовский стационарный шум с дисперсией ²=1,3392∙10 Вт.

Приемник, оптимальный по критерию идеального наблюдателя (минимума средней вероятности ошибки), принимает решение по одному отсчету смеси сигнала и помехи

Z(t₀) = S_i(t₀ )+ (t₀) = 0,8215∙10^-3 в, на интервале элемента сигнала длительности c.

Амплитуда канальных сигналов А = 3,2863∙10 В.

Задание:

Найти и изобразить графически кривые плотностей распределения W() и условных вероятностей W(z/0) и W(z/1).

Показать на графике значения A, , z(t₀).

Определить, какой символ ("1" или "0") будет зарегистрирован приемником, используя отношение правдоподобия. Предварительно пояснив, что такое отношение правдоподобия, привести общее выражение для его вычисления применительно к варианту задания и сделать необходимые расчеты.

Привести выражение и поясните смысл критерия идеального наблюдателя.

Выполнение:

Если бы на входе приемника отсутствовали помехи, то задача разделения сигналов была бы очень проста. При наличии же помех сигналы искажаются, и для их описания приходится использовать вероятностное пространство. Сигналы вместе с помехами описываются функциями плотности вероятности (z/s

---

₁) и (z/s₂), где (z/s_i) представляет собой плотность вероятности того, что принятый сигнал Z образовался при передаче сигнала S_i, также называется функцией правдоподобия.

Отношение называется отношением правдоподобия, и чем больше значение (Z/S_i), тем более вероятно, что Z содержит сигнал S_i

Выражение 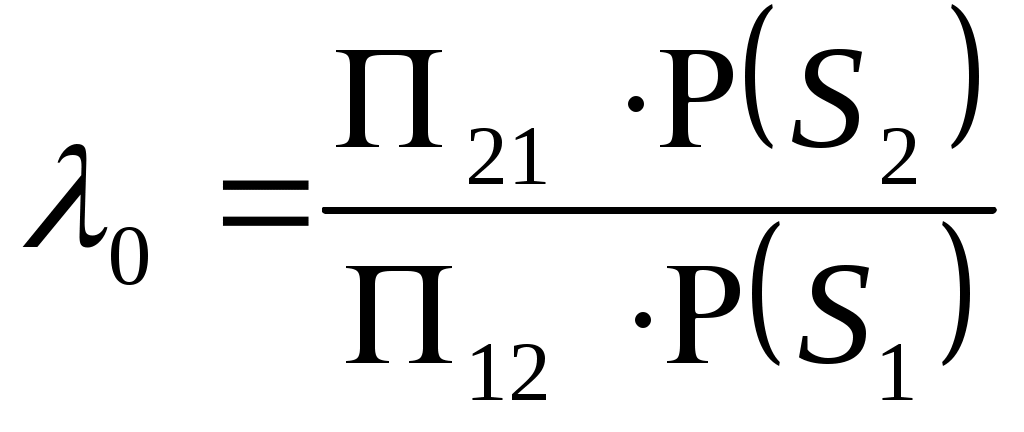называется пороговым отношением правдоподобия.

Приемник вычисляет отношение правдоподобия (z), и далее по известным априорным вероятностям P(s₁) и P(s₂) и весовым коэффициентам ₁₂, ₂₁ (риск), вычисляется пороговое отношение правдоподобия ₀.

Если (z) > _0, то приемник выдает сигнал S₁, если нет то сигнал S₂.

Приём сигналов фазовой модуляции возможен только с помощью синхронного (когерентного) детектора, различающего фазы принимаемых сигналов.

Помеха в канале связи (флуктуационная) с нормальным законом распределения мгновенных значений.

w () =

Плотность вероятности сигнала Z(t) = S_i(t)+ (t) имеет вид.

w (Z/S₁) =

w (Z/S₂) =

При отсутствии сигнала, плотность вероятности будет находиться по формуле

.

А
лгоритм различения двух и более сигналов на фоне белого Гауссовского шума по методу идеального наблюдателя имеет следующий смысл – наиболее вероятным переданным сигналом считается тот сигнал, который меньше отличается от принятого сигнала. Таким образом, оптимальный приемник манипулирует средней вероятностью ошибки. В аналитической форме алгоритм оптимального приемника имеет вид:

если это условие выполняется то принимаем S₁(t), иначе S₂(t).

---

Результаты вычислений

Z,10-3	-8,29	-7,29	-6,29	-5,29	-4,29
W(z/S1)	4,93789∙10-20	1,9245∙10-16	3,555∙10-13	3,112∙10-10	1,29∙10-7
W(z/S2)	0,022667994	0,652733554	8,9076845	57,610248	176,57967
W()	1,88637∙10-10	6,31942∙10-7	0,0001003	0,0075491	0,2691929

Z,10-3	-3,29	-2,29	-1,29	0	1,29	2,29	3,29
W(z/S1)	2,53798∙10-5	0,00236481	0,1044263	4,5492303	57,610248	176,57967	256,50018
W(z/S2)	256,5001848	176,579669	57,610248	4,5492303	0,1044263	0,0023648	2,538∙10-5
W()	4,549230307	36,43495242	138,29438	256,50018	138,29438	36,434952	4,5492303

Z,10-3	4,29	5,29	6,29	7,29	8,29
W(z/S1)	176,579669	57,61024822	8,9076845	0,6527336	0,022668
W(z/S2)	1,29088E-07	3,11166E-10	3,555E-13	1,925E-16	4,938E-20
W()	0,269192944	0,007549105	0,0001003	6,319E-07	1,886E-09

---

График рассчитанных плотностей вероятностей.

; ;



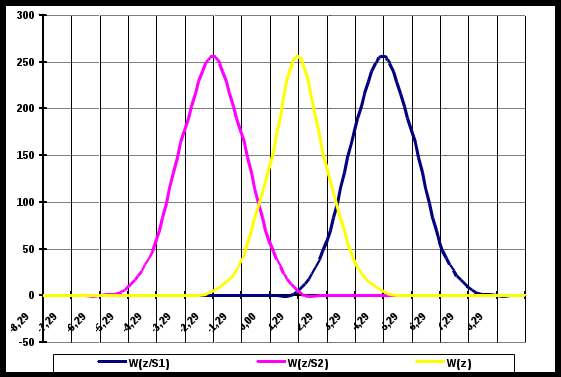
Рисунок 3. Кривые плотностей распределения W(), W(z/0) и W(z/1).

В данном случае приемник, оптимальный по критерию идеального наблюдателя (минимума средней вероятности ошибки), последствия ошибок и равнозначны и весовые коэффициенты ₁₂= ₂₁=1, тогда средняя вероятность ошибки минимизируется:



P(Z_i/S_j) - условные вероятности ошибочного приема, чем она меньше тем меньше вероятность ошибки.

P(S_i) - априорные вероятности излучения.

Отсюда найдем пороговое отношение правдоподобия:






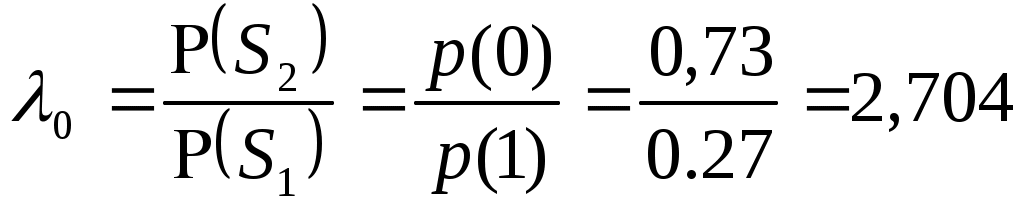
Отношение правдоподобия:


(z)>₀, (56,36>2,704), значит приемником будет зарегистрирован символ ("1").
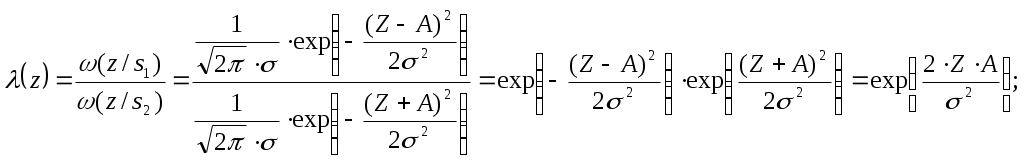
3.4. Вероятность ошибки на выходе приемника.

Данные:

Вид сигнала в канале связи – (ДФМ).

Способ приема сигнала (КГ).

Задание:

Рассчитать вероятность неправильного приема двоичного символа (среднюю вероятность ошибки) в рассматриваемом приемнике для вида сигнала (ДФМ) и способа приема (КГ), а также зависимость p(h).

Построить график p(h) для 4-5 значений h с учетом реальной полосы пропускания приемника (на этом графике показать точку, соответствующую рассчитанной величине

---

h и вычисленной вероятности ошибки).

Выполнение:

Средняя вероятность ошибки при ДФМ равна

.

Рассчитаем среднюю вероятность ошибки для заданного вида сигнала и способа приема:

;



Оптимальная полоса пропускания фильтра:

Гц; .

Т - длительность элемента сигнала.

В итоге: Гц.

Таблица зависимости .

h	0	0,5	1	2	2,5	3
	0,5	0,24196	0,08076	0,002255	1,93*10-4	3,2*10-5

График зависимости .



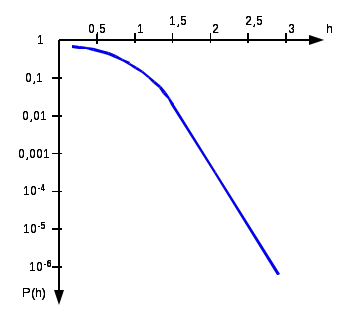
Рисунок 4. Зависимость .

3.5. Выигрыш в отношении сигнал/шум при применении оптимального приемника.

Задание:

В предположении оптимального приема (фильтрации) сигналов определить:

выигрыш в отношении сигнал/шум оптимального приемника по сравнению с рассчитываемым;

максимально возможное отношение сигнал/шум h²₀;

Выполнение:

При оптимальной фильтрации основная задача – обеспечение максимального отношения мощности сигнала к мощности помехи на выходе.

---

Смотрите также файлы

• Состав и строение солнечной системы.docx

• Разработка 3D модели вращающегося пневмоцилиндра.docx

• Государственная итоговая аттестация по образовательным программам основного общего образования в форме основного государственного экзамена (огэ).pdf

• Предмет и задачи психогигиены. Понятие психического здоровья. Вопросы к семинару.docx

• Алгоритм выполнения.docx