РУ

(t) Y(t)







S₂


Синхро



СФ – согласованный фильтр.

РУ – решающее устройство.

Y(t) – сигнал на выходе СФ.
Решающее устройство в момент окончания сигнала на входе СФ проверяет фазу полученного после СФ сигнала и соответственно выносит решение в пользу S₁ или S₂.
Структурная схема асинхронного приемника.
S₁

Z
СФ

РУ

(t) Y(t)







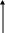
S₂

U_п1 U_п2
Решающее устройство в любой момент времени сравнивает полученный после СФ сигнал с пороговым напряжением, если Y(t) U_п1 , если Y(t) U_п2 ,а если не выполняется не одно из этих условий, то решение не принимается.

Синхронный приемник обладает лучшей помехоустойчивостью, чем асинхронный, так как в синхронном приемнике мощность помехи меньше из – за (дискретного) принятия решения в момент окончания сигнала на входе СФ (когда сигнал на выходе СФ максимален).
3.15. Энергетический выигрыш при применении согласованного фильтра

---

Задание:

Определить энергетический выигрыш при приеме сигналов с использованием согласованного фильтра (пояснить, за счет чего и какой ценой достигается этот выигрыш).

Выполнение:

Согласованный фильтр обеспечивает при флуктуационной помехе в канале типа «белого шума», в момент окончания сигнала t₀ = Т_с, на своём выходе максимально возможное отношение пиковой мощности сигнала к мощности помехи. Выигрыш в отношении сигнал/шум на выходе СФ по сравнению со входом равняется базе сигнала (В = 2·F_с·Т_с), т. е.
,

где Т_с = NТ – длительность сигнала (N - число элементов в дискретной последовательности);

– ширина спектра сигнала.

Таким образом, выигрыш q = (h_вых)² / (h_вх)², обеспечиваемый СФ при приёме дискретных последовательностей, составляет N раз. Следовательно, путём увеличения длины дискретных последовательностей, отображающих символы сообщений 1 и 0, можно обеспечить значительное повышение отношения сигнал/шум на входе решающей схемы приёмника и, соответственно, повышение помехоустойчивости передачи дискретных сообщений. Очевидно, что это будет приводить к снижению скорости передачи сообщений.

При приеме сложного сигнала оптимальным фильтром действует метод накопления , в результате чего энергетический выигрыш равен:

;

где N – количество элементарных сигналов в сложном сигнале.

; ;

энергетический выигрыш достигается ценой уменьшения скорости передачи информации.
3.16. Вероятность ошибки на выходе приемника при применении сложных сигналов и согласованного фильтра.
При определении вероятности ошибки считаем, что сигналы, соответствующие символам "1" и "0", являются взаимно противоположными и решение о переданном символе принимается с использованием

---

пороговой решающей схемы синхронным способом, (отсчеты берутся в конце каждого сигнала длительностью kT, где T - длительность одного элемента сложного сигнала). При этом считаем, что длительность сигнала возросла в k раз по сравнению со случаями использования простых сигналов, где k - количество элементарных посылок в сложном сигнале.

Для определения вероятности ошибки на выходе при применении согласованного фильтра воспользуемся формулой:



Для различных методов приема приведем Р_ош:

• 
  Метод однократного отсчета при неоптимальном приемнике Р_ош=0,0023
  
• 
  Метод трехкратного отсчета при неоптимальном приемнике Р_ош0
  
• 
  Идеальный приемник Котельникова Р_ош0
  
• 
  Прием с помощью оптимального фильтра Р_ош0
  

Вывод: метод однократного отсчета имеет небольшую помехоустойчивость, т.к. производится всего один отсчет. При увеличении числа отсчетов вероятность ошибки уменьшается. Идеальный приемник Котельникова даст максимальную помехоустойчивость. Согласованный фильтр обеспечивает максимально возможное отношение сигнал/шум, что уменьшает вероятность ошибки.
3.17. Пропускная способность разработанной системы связи (Энтропия).
Пропускной способностью системы связи называется максимально возможная способность передачи информации.

Вычислим пропускную способность непрерывного канала связи. По формуле Шеннона для известной полосы пропускания f_пр=18∙10³ Гц, а также отношения сигнал/шум по мощности h₀²=16,13.

С=f_пр*log₂(1+ h₀²)= 18∙10^3∙3,18=57,24∙10³ Бит/с=57,24 кБит/с.

Пропускная способность равна “производительности” источника сообщений, обозначим ее B’©. Суммарная энтропия пусть будет В(С). Тогда

В(С)=Р(0)∙log₂(1/Р(0))+ Р(1)∙log₂(1/Р(1))=0,73∙1,37+0,27∙3,704=0,841

В^’(С)=В(С)/Т=В(С)∙V=0,841∙9000=7,569∙10³

Найдем эффективную пропускную способность непрерывного канала связи, т.е.





Так как пропускная способность канала связи оказалась больше “производительности” источника, то возможна передача информации по данному каналу.

---

СПИСОК ЛИТЕРАТУРЫ:

1. Теория электрической связи: Учебник для вузов / А. Г. Зюко, Д. Д. Кловский, М. В. Назаров, Ю. Н. Прохоров.—М.: Радио и связь (в печати).

2. 
   Теория передачи сигналов: Учебник для вузов / А. Г. Зюко, Д. Д. Кловский,
   

М. В. Назаров, Л.М. Финк.—2-е изд., перераб. и доп.—М.: Радио и связь, 1986.—304 с.

2. 
   Макаров А.А., Чиненков Л.А. Основы теории помехоустойчивости дискрет-ных сигналов: Учеб. пособие.— Новосибирск, СибГАТИ, 1997.—42 с.
   
3. 
   Макаров А.А. Методы повышения помехоустойчивости систем связи.—Новосибирск, СИИС, 1991.—58 с.
   

---

Смотрите также файлы

• Состав и строение солнечной системы.docx

• Разработка 3D модели вращающегося пневмоцилиндра.docx

• Государственная итоговая аттестация по образовательным программам основного общего образования в форме основного государственного экзамена (огэ).pdf

• Предмет и задачи психогигиены. Понятие психического здоровья. Вопросы к семинару.docx

• Алгоритм выполнения.docx