Файл: Контрольная работа по дисциплине математика для студентов заочного отделения всех специальностей (бакалавриат).docx
Добавлен: 17.03.2024
Просмотров: 52
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
контрольная работа
по дисциплине «математика»
для студентов заочного отделения всех специальностей (бакалавриат)
указания к выполнению
контрольной работы
Домашняя контрольная работа студента должна удовлетворять следующим требованиям:
-
Вариант контрольной работы выбирается по последней цифре номера зачетной книжки студента. Например, если номер оканчивается на 3, то ему соответствует вариант 3, и следует выбирать в контрольной работе задачи 1.3, 2.3, 3.3, 4.3, 5.3, 6.3, 7.3, 8.3, 9.3. Если номер зачётной книжки оканчивается на 0, то ему соответствует вариант 10. -
Работу следует выполнить в отдельной 12-ти страничной тетради. На титульном листе необходимо указать фамилию, имя и отчество студента; номер группы; название института; дисциплину, а также номер варианта контрольной работы. -
Перед решением задачи должно быть полностью приведено её условие. -
Решение задач следует сопровождать необходимыми формулами, развернутыми расчётами, расчётными таблицами и краткими пояснениями.
Содержание контрольной работы
Задача 1. Область определения функции. Найти области определения функций одной переменной:
1.1. а)
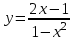 ; б)
; б) 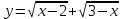 .
.1.2. а)
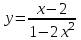 ; б)
; б) 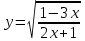 .
.1.3. а)
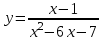 ; б)
; б) 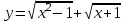 .
.1.4. а)
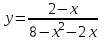 ; б)
; б) 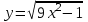 .
.1.5. а)
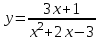 ; б)
; б) 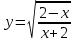 .
.1.6. а)
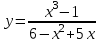 ; б)
; б) 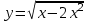 .
.1.7. а)
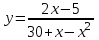
; б)
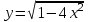 .
.1.8. а)
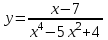 ; б)
; б) 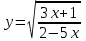 .
.1.9. а)
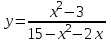 ; б)
; б) 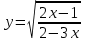 .
.1.10. а)
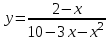 ; б)
; б) 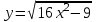 .
.Задача 2.Предел функции одной переменной.
Найти пределы, не применяя дифференциальное исчисление (правило Лопиталя):
2.1. а)
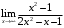 , б)
, б)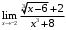 , в)
, в)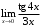 , г)
, г)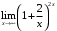 .
.2.2. а)
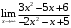 , б)
, б)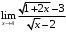 , в)
, в)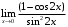 , г)
, г)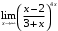 .
.2.3. а)
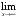
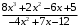 , б)
, б)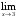
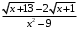 ,
, в)
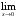
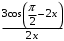 , г)
, г)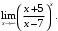
2.4. а)
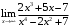 , б)
, б)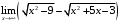 ,
,в)
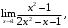 г)
г)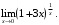
2.5. а)
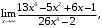 б)
б)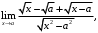
в)
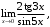
 г)
г)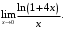
2.6. а)
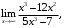 б)
б)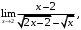 в)
в)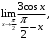 г)
г)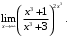
2.7. а)
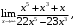 б)
б)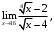 в)
в)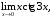 г)
г)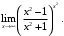
2.8. а)
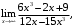 б)
б)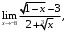 в)
в)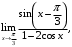 г)
г) 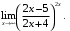
2.9. а)
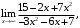 б)
б)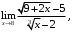
в)
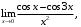 г)
г)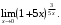
2.10. а)
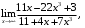 б)
б)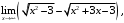
в)
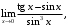 г)
г)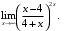
Задача 3. Дифференциальное исчисление функций одной переменной.
Найти производные первого порядка функций:
3.1. а)
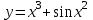 , б)
, б) 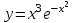 .
.3.2. а)
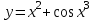 , б)
, б) 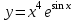 .
.3.3. а)
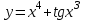 , б)
, б) 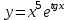 .
.3.4. а)
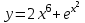 , б)
, б) 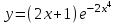 .
.3.5. а)
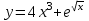 , б)
, б) 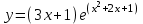 .
.3.6. а)
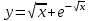 , б)
, б) 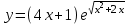 .
.3.7. а)
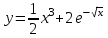 , б)
, б) 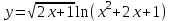 .
.3.8. а)
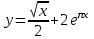 , б)
, б) 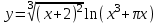 .
.3.9. а)
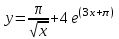
, б)
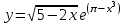 .
.3.10. а)
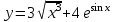 , б)
, б) 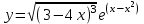 .
.Задача_4._Приложения_дифференциального_исчисления_функций_одной_переменной.'>Задача 4. Приложения дифференциального исчисления функций одной переменной.
Найти наименьшее и наибольшее значения функции y=f(x) на заданном отрезке [a;b]:
4.1. f(x)=x3-12x+7, [0;3].
4.2. f(x)=x4-4x3+6x2 +7, [-1;3].
4.3. f(x)=x3+3x2 -7, [-1;2].
4.4. f(x)=2x(x-1)3, [0,5;2].
4.5. f(x)=x3-3x2 -45x+10, [1;6].
4.6. f(x)=x3+4x2 , [-1;1].
4.7. f(x)=x3-5x+1, [0;1].
4.8. f(x)=2x3-3x2+1, [0;2].
4.9. f(x)=x4-3x2, [-1 ;2].
4.10. f(x)=x3-4x2-1, [ -2;1].
Задача 5. Исследование функций и построение графиков.
Исследовать функцию и построить её график:
5.1.
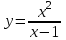 . 5.2.
. 5.2. 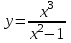 .
.5.3.
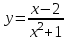 . 5.4.
. 5.4. 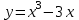 .
.5.5.
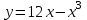 . 5.6.
. 5.6. 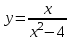 .
.5.7.
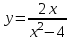 . 5.8.
. 5.8. 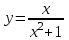 .
.5.9.
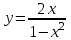 . 5.10.
. 5.10. 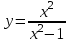 .
.Задача 6. Матрицы и операции над ними.
Заданы матрицы A, B, C. Найти матрицы (если они существуют):
2A-3B; 5(A+B+E); A+C; A∙B; B∙A; A∙BT ; A∙C; A∙TC; C∙BT.
Здесь E– единичная матрица, T - знак транспонирования матрицы. Если какая-либо из матриц не существует, то объяснить причину.
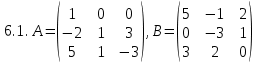
, C=
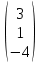 .
.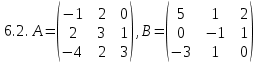 , C=
, C=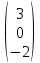 .
.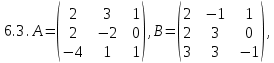 C=
C=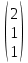 .
.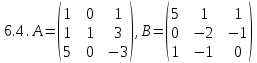 , C=
, C=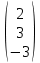 .
.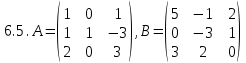 , C=
, C=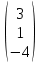 .
.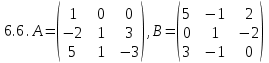 , C=
, C=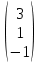 .
.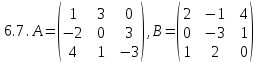 , C=
, C=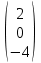 .
.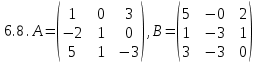 , C=
, C=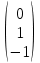 .
.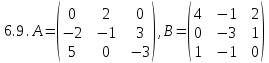 , C=
, C= .
.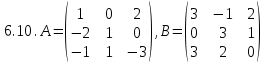 , C=
, C=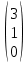 .
.Задача 7. Вычисление определителей и миноров.
Вычислить определитель четвёртого порядка.
7.1.
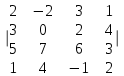 7.2.
7.2. 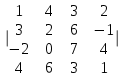
7.3.
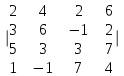 7.4.
7.4. 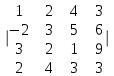
7.5.
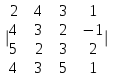 7.6.
7.6. 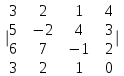
7.7.
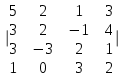 7.8
7.8 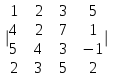
7.9.
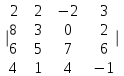 7.10.
7.10. 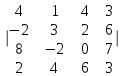
Задача 8. Векторы и операции над ними.
Точки А, В, С пространства заданы своими координатами в прямоугольной декартовой системе координат. Найти:
-
векторы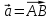 ,
,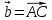 ,
,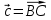 ;
; -
скалярное произведение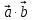 ;
; -
векторное произведение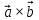 и его модуль;
и его модуль; -
величины углов, длины сторон и площадь треугольника АВС; -
смешанное произведение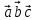 ;
; -
уравнение плоскости, проходящей через точки A, B, C.
