ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.03.2024
Просмотров: 113
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
к средней арифметической величине:
V σ 100 %.
x
Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однород- ности совокупности. Совокупность считается количественно однородной,если коэффициент вариации не превышает 33 %.
Известны данные о сменной выработке рабочих бригады, представ- ленные интервальным рядом распределения (табл. 20).
Таблица20
Определяем среднесменную выработку:
x x f
f
21600 216 шт.
100
Рассчитываем дисперсию выработки:
x x2 f 30400
σ2 304 .
f 100
Находим среднеквадратическое отклонение:
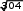σ 17, 44
Определяем коэффициент вариации:
шт.
V σ 100 17, 44100 8 %.
x 216
Таким образом, данная бригада рабочих достаточно однородна по вы- работке, поскольку вариация признака составляет лишь 8 %.
Вариация признака обусловлена различными факторами, некоторые из которых можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку. Тогда, наряду с изучением вариации признака по всей совокупности в целом, становится возможным изучить вариацию для каждой из составляющих ее группы, а также и между этими
группами. В простейшем случае, когда совокупность расчленена на груп- пы по одному фактору, изучение вариации достигается посредством ис- числения и анализа трех видов дисперсий: общей, межгрупповой и внутри- групповой.
Общаядисперсияσ2
измеряет вариацию признака по всей совокуп-
ности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака х от общей средней xи может быть вычислена как простая или взвешеннаядисперсия:
n
x x2
x x2 f
i
σ2 i1
или
i i
n
n
σ2 i1 .
i
n f
i1
Межгрупповаядисперсияδ2
характеризует систематическую вариа-
цию результативного признака, обусловленную влиянием признака- фактора, положенного в основание группировки. Она равна среднему
квадрату отклонений групповых средних
xiот общей средней x:
n
x x2 f
i i
n
δ2 i1 ,
fi
i1
где f - численность единиц в группе.
σ
Внутригрупповая(частная)дисперсия
2 отражает часть вариации,
i
обусловленную влиянием неучтенных факторов и не зависящую от при- знака-фактора, положенного в основание группировки. Она равна средне- му квадрату отклонений отдельных значений признака внутри группы х
от средней арифметической этой группы
xi и может быть вычислена как
простаяили как взвешеннаядисперсиясоответственно:
n
x x2
x x2 f
i i
σ2 i1
или
i i i
n
σ2 i1 .
i n i n
fi
i1
На основании внутригрупповой дисперсии по каждой группе, т. е. на ос-
i
новании
персий:
σ2 , можно определить общую среднююизвнутригрупповыхдис-
σ f
n
2
i i
i n
σ2 i1 .
fi
i1
Согласно правилу сложения дисперсий общая дисперсия равна сум- ме средней из внутригрупповых и межгрупповой дисперсий:
i
σ2 σ2 δ2 .
Пользуясь правилом сложения дисперсий, можно всегда по двум из- вестным дисперсиям определить третью - неизвестную, а также судить о силе влияния группировочного признака.
При изучении влияния квалификации рабочих на уровень производи- тельности труда в цехе были получены данные, представленные в табл. 21. В примере данные группируются по тарифному разряду рабочих, яв-
ляющемуся факторным признаком x.
y 60 10
шт.;
1 6
y 60 15
шт.;
2 4
n
n
yi fi
10 6 15 4
yi1 12
шт.
Таблица21
10
fi
i1
Данные для расчета дисперсий по группам приведены в табл. 21.
По данным определяем:
n
y y2
2 i i 24
n 6
n
y y2
V σ 100 %. xКоэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однород- ности совокупности. Совокупность считается количественно однородной,если коэффициент вариации не превышает 33 %.
Пример 10
Известны данные о сменной выработке рабочих бригады, представ- ленные интервальным рядом распределения (табл. 20).
Таблица20| Группы рабочих по величине выработ- ки, шт. | Число ра- бочих f | Середина интервала x | Расчетные значения | |
| x f | x x2 f | |||
| 170–190 | 10 | 180 | 1800 | 12960 |
| 190–210 | 20 | 200 | 4000 | 5120 |
| 210–230 | 50 | 220 | 11000 | 800 |
| 230–250 | 20 | 240 | 4800 | 11520 |
| Итого | 100 | – | 21600 | 30400 |
Определяем среднесменную выработку:
x x f f
21600 216 шт.
100
Рассчитываем дисперсию выработки:
x x2 f 30400 σ2 304 .
f 100
Находим среднеквадратическое отклонение:
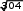σ 17, 44Определяем коэффициент вариации:
шт.
V σ 100 17, 44100 8 %.x 216
Таким образом, данная бригада рабочих достаточно однородна по вы- работке, поскольку вариация признака составляет лишь 8 %.
- 1 2 3 4 5 6 7 8
Правило сложения дисперсий
Вариация признака обусловлена различными факторами, некоторые из которых можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку. Тогда, наряду с изучением вариации признака по всей совокупности в целом, становится возможным изучить вариацию для каждой из составляющих ее группы, а также и между этими
группами. В простейшем случае, когда совокупность расчленена на груп- пы по одному фактору, изучение вариации достигается посредством ис- числения и анализа трех видов дисперсий: общей, межгрупповой и внутри- групповой.
Общаядисперсияσ2
измеряет вариацию признака по всей совокуп-
ности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака х от общей средней xи может быть вычислена как простая или взвешеннаядисперсия: n
x x2
x x2 f
i
σ2 i1
или
i i
n
n
σ2 i1 .
i
n f
i1
Межгрупповаядисперсияδ2
характеризует систематическую вариа-
цию результативного признака, обусловленную влиянием признака- фактора, положенного в основание группировки. Она равна среднемуквадрату отклонений групповых средних
xiот общей средней x:
n
x x2 f
i i
n
δ2 i1 ,
fi
i1
где f - численность единиц в группе.
σ
Внутригрупповая(частная)дисперсия
2 отражает часть вариации,
i
обусловленную влиянием неучтенных факторов и не зависящую от при- знака-фактора, положенного в основание группировки. Она равна средне- му квадрату отклонений отдельных значений признака внутри группы х
от средней арифметической этой группы
xi и может быть вычислена как
простаяили как взвешеннаядисперсиясоответственно:
n
x x2
x x2 f
i i
σ2 i1
или
i i i
n
σ2 i1 .
i n i n
fi
i1
На основании внутригрупповой дисперсии по каждой группе, т. е. на ос-
i
новании
персий:
σ2 , можно определить общую среднююизвнутригрупповыхдис-
σ f
n
2
i i
i n
σ2 i1 .
fi
i1
Согласно правилу сложения дисперсий общая дисперсия равна сум- ме средней из внутригрупповых и межгрупповой дисперсий:
i
σ2 σ2 δ2 .
Пользуясь правилом сложения дисперсий, можно всегда по двум из- вестным дисперсиям определить третью - неизвестную, а также судить о силе влияния группировочного признака.
Пример 11
При изучении влияния квалификации рабочих на уровень производи- тельности труда в цехе были получены данные, представленные в табл. 21. В примере данные группируются по тарифному разряду рабочих, яв-
ляющемуся факторным признаком x.
-
Для расчета групповых дисперсий исчисляем средние выработки по каждой группе и общую среднюю выработку:
-
по I группе
y 60 10
шт.;
1 6-
по II группе
y 60 15
шт.;
2 4 n
n
yi fi
10 6 15 4-
по двум группам
yi1 12
шт.
Таблица2110
fi
i1
| № п/п | Рабочие IV разряда | № п/п | Рабочие V разряда | ||||||
| Выработка рабочего, шт., y | y y | y y2 | Выработка рабочего, шт., y | y y | y y2 | ||||
| 1 | 7 | –3 | 9 | 1 | 14 | –1 | 1 | ||
| 2 | 9 | –1 | 1 | 2 | 14 | –1 | 1 | ||
| 3 | 9 | –1 | 1 | 3 | 15 | 0 | 0 | ||
| 4 | 10 | 0 | 0 | 4 | 17 | –2 | 4 | ||
| 5 | 12 | 2 | 4 | | | | | ||
| 6 | 13 | 3 | 9 | | | | | ||
| | 60 | – | 24 | | 60 | – | 6 | ||
Данные для расчета дисперсий по группам приведены в табл. 21.
По данным определяем:
n
y y2
2 i i 24
- по первой группе: σ1 i1 4 ;
n 6
n
y y2
-
i i 6