ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.03.2024
Просмотров: 33
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
соподчиненныминазываются виды одного и того же рода. Например, «поэзия» и «архитектура» являются понятиями, подчиненными одному родовому для них понятию «искусство». Отношение соподчинения наглядно можно изобразить в виде круговой схемы:
П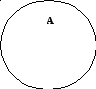
ри этом родовое понятие называется подчиняющим, а видовые – соподчиненными. При оперировании соподчиненными понятиями надо иметь в виду два правила несовместимости. Первое правило: соподчиненные понятия должны быть ближайшими видами одного общего для них рода. Несоблюдение данного правила приводит к ошибке соподчинения видовых понятий, принадлежащих разным родовым понятиям. Второе правило: соподчиненные понятия не должны находится в отношении пересечения.
Вторым видом отношений между несовместимыми понятиями является отношение противоположности. Два соподчиненных понятия называются противоположными(контрарными), если одно из них содержит такие признаки, которые исключает другое понятие, замещая их на противоположные. Имена таких понятий выражаются в языке антонимами. Например, «тяжелое» и «легкое», «далекое» и «близкое» и т.п. Отношение противоположности присуще таким видовым понятиям, которые находятся на крайних полюсах рода. Иллюстрацией такого положения может служить схема:
О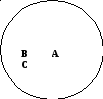
ба противоположных понятия «белое» (В) и «черное» (С) входят в объем подчиняющего понятия «цвет» (А), но полностью всего объема подчиняющего понятия не исчерпывают. Между противоположными понятиями существуют промежуточные виды со своими признаками. Между крайними противоположностями белого и черного цветов можно последовательно перечисляя объем средний части перейти от одного к другому, и наоборот.
Третьим видом отношений между несовместимыми понятиями является отношение противоречия. Противоречащими
(контрадикторными) называются соподчиненные понятия, которые исключают друг друга и оба вместе полностью исчерпывают объем родового понятия. Отношение противоречия графически изображается так:
Н
апример, «белый» и «небелый». В отношении противоречия находятся положительные и отрицательные понятия. Оба эти понятия одновременно и в одном отношении нельзя применить к одному и тому же предмету не впадая в логическое противоречие. Древнегреческий поэт Феогнид из Мегар (VIв. до н.э.) подвел безрадостный итог совей жизни в такой контрадикторно сформулированной сентенции:
«Сделав, я не сделал и не закончил, закончив;
совершив, не совершил и достигнул, не достигнув».1
Для того, чтобы отличить противоположные и противоречащие понятия, следует придерживаться двух правил: 1) противоречащие – это пара понятий, одно из которых положительное, а другое – отрицательное; противоположные понятия оба положительны; 2) противоречащие понятия оба вместе исчерпывают класс предметов, мыслимых в понятии; противоположные – не исчерпывают весь объем родового понятия.
Отношение противоречия и противоположности выполняют особую роль в логическом рассуждении. Каждое из них может достигать такой интенсивности и такого утончения, когда одно превращается в другое. Полемика об этих понятиях до сих пор не приводит к полному удовлетворению.
В ряду противоположных понятий есть такие, которые находятся в отношении бинарной оппозиции (лат. оppositio– противопоставление). Существуют три вида бинарной оппозиции. 1) Прямое противопоставление, при котором два понятия контрарны по содержанию, то есть оба являются положительными, но в своей совокупности исчерпывают весь объем родового понятия. Между содержаниями таких понятий имеет место двусторонняя импликация. Например, «правый» и «левый», «верх» и «низ», «восток» и «запад», «плюс» и «минус», «истина» и «ложь» и т.п. Один выступает антиподом другого. 2) Косвенное противопоставление (ослабленная оппозиция), при котором два понятия контрадикторны по содержанию, то есть одно из них положительное, а другое – отрицательное, но в своей совокупности они не исчерпывают всего объема родового понятия. Между содержаниями таких понятий возможна только односторонняя импликация. Например, «старый» и «нестарый». Между такими понятиями существуют промежуточные виды («зрелый», «пожилой» и т.п.). Из содержания одного («старый») не следует содержание другого («молодой»). Пример амбивалентного отношения: «любовь – ненависть». 3) Конверсная оппозиция, при которой фиксируется контраст сравниваемых понятий (оба положительные), их резкое противопоставление. Например, «лед» и «пламя», «умный» и «дурак» и т.п.
2
В свою очередь бывает, хотя и редко, ситуация, при которой соподчиненные понятия исчерпывают весь объем родового понятия и при этом не являются противоречащими. Например, «простое предложение» и «сложное предложение». Они исчерпывают все виды предложений, выделенных с указанной точки зрения.
Анализ круговых схем показывает, что попытка выдержать требование выявления отношений между двумя произвольно взятыми сравнимыми понятиями наталкивается на ряд серьезных затруднений и, прежде всего на ситуацию, принуждающую вводить третье понятие, без которого вид отношения между двумя понятиями не может быть установлен. Так, обсуждение двух соподчиненных понятий обнаруживает, что отношение соподчинения принуждает мыслить еще одно (третье) понятие, подчиняющее каждое из них. В противном случае отношение соподчинения исчезает. На круговых схемах они принимают вид несравнимых понятий, но это противоречит их смыслу, поскольку они являются ближайшими видами своего родового понятия. Данное обстоятельство приводит к необходимости введения отношения подчинения, которое, в свою очередь, не присущее несовместимым понятиям. К тому же ряд отношений между понятиями в круговых схемах просто невыразимы. Еще раз подчеркнем, что для выявления отношений между понятиями были приняты условия: 1) выявляются и анализируются отношения, присущее двум совместимым понятиям (осуществляется по парный анализ понятий); 2) для ясности и определенности возможных отношений рассматриваются только простые понятия.
Осуществим второй семантический подход для интерпретации и наглядного представления отношений между простыми понятиями, который задается модельными схемами, является их полным перечнем и снимает ряд затруднений, встречающихся в круговых схемах Эйлера. Такие модельные схемы были предложены Кейнсом в 1906 году.
Предположим, даны два понятия x A(x) иxB(x) и пусть родом первого понятия будетU, а второгоU. Если универсумы U иU2различны и в них нет ни одного совпадающего элемента, то они являются несравнимыми. Так, если два понятия, одно из которыхxА (х), скажем "мудрость" принадлежит универсумуU, а второе -x B(x), например, «голубизна», относится к универсумуU2, то объединение таких универсумов образует нелепость. В качестве подобных примеров можно привести образование универсумов, представляющих универсумы разного порядка, таких как вещи и ее части, вещи и ее свойства и т.п. Возникновение универсумов такого рода приводит к противоречиям и парадоксам. Стало быть, запрет на объединение несравнимых понятий правомерен из-за возможных противоречий образуемого из них общего универсума. Такого рода универсумы не могут совпадать между собой.
Если роды двух понятий совпадают хотя бы в единственной своей части, то имеют место сравнимые понятия. Именно о таких универсумах и отношениях, в которых могут находиться сравнимые понятия, строится новая семантика. Особенностью данной семантики является допущение пустых универсумов, то есть областей реально несуществующих объектов и, следовательно, понятий, объем которых пуст, непустых универсумов и таких универсумов, когда родовое понятие совпадает с универсумом рассуждения. Получим следующий перечень модельных схем:
..
Выделим из числа сравнимых понятий три фундаментальных отношения.
1) Отношение совместимостиимеет место тогда и только тогда, когда пересечение объемов понятий х А (х) и хB(х) не являются пустыми:
WхА(х)∩ WхВ(х)
Запись можно упростить так: А∩В ≠ Ø Отношение совместимости означает, что должен существовать хотя бы один предмет, для содержания которого было бы вернох(А(х)В(х)). На модельных схемах такому отношению соответствуют 4, 7, 8, 9, 10, 11, 12 и 15 схемы.
2) Отношение исчерпыванияимеет место тогда и только тогда, когда объединение понятий х А(х) и хВ(х) совпадает с универсумом:
Wх А(х)UWхВ(х)=U
В упрощенной записи: АUB=U. Содержание понятий, находящихся в отношении исчерпываниях(А(х)VB(х)) равно универсуму. На модельных схемах такому отношению соответствуют 2, 3, 4, 7, 8, 14 и 15 схемы.
3) Отношение включения имеет место тогда и только тогда, когда одно понятиевходит в объем другого понятия. Для двух понятий хА(х) и хВ(х) отношение включения выполняется при условии:
(WхА(х)WхВ(х))V(Wх В(х)WхА(х)).
В упрощенной записи будем иметь (АВ)V(ВА), где "" знак нестрогого включения. Для содержания этих понятий достаточно, что х (А(х)В(х)), либох(В(х)А(х)). На модельных схемах такому отношению соответствуют 5, 6, 7, 8, 10 и 11, а так же 1, 2, 3, 4 и 9 схемы как предельные случаи.
Указанные три вида отношений получили название фундаментальных в силу того, что их различные сочетания порождают все другие возможные отношения между двумя сравнимыми понятиями, образуяпроизводные отношения. Из числа таких производных отношений назовем следующие.
1) Отношение несовместимости .Два понятия хА(х) и хВ(х) находятся в отношении несовместимости, если и только если, их пересечение пусто
WхА(х)∩WхВ(х)=Ø,
или кратчайшим образом: А∩В= Ø. Их содержания отвечают требованию ┐х(А(х)&B(х)).
2) Отношение неисчерпывания. Два понятия хА(х) и хВ(х) находятся в данном отношении, если и только если их объединение не образует полного универсума
Wх А (х)UWхВ(х) ≠U,
или кратко: АUВ ≠U. Их содержания удовлетворяют условию: ┐х(А(х)VВ (х)).
3) Отношение подчинения. Понятия хА(х) и хВ(х) находятся отношении подчинения, если имеет место включения объема одного из них в объем другого. Припрямом включении объем второго понятия полностью входит в объем первого понятия. В упрощенной записи это можно указать так (АВ). Приобратномвключении понятие В находится в объеме А: (ВА).
Пустое понятие включается в любое другое понятие. Так, если из двух понятий хА(х) ихВ(х), хотя бы одно пусто, то его включение может быть записано так:
(WхА(х)= Ø)(WхА(х)WхВ(х),
или иначе: для всякого В верно, что В(ØВ).Аналогично в другом случае.
Если из двух понятий хотя бы одно является универсальным классом, то есть совпадает с униерсумом, то для х А(х) их В (х) будет верно
(Wх А (х) =U)(Wх В (х)Wх А (х)),
или иным способом записи: для всякого В верно, что (В U).
Аналогично в другом случае.
Как прямое, так и обратное включение может быть строгим или нестрогим. Отношение строгого включения характеризуется тем, что объем понятия хА(х) строго включается в объем понятия хВ(х), если выполняется условие:
(АВ) & ┐(ВА),
в кратчайшей записи АВ. В этой ситуации хА(х) есть вид, а хВ(х)- род, и где "" -знак отношения строгого включения. В другом случае , при котором второе понятие включено в объем первого, то верным будет условие: (ВА).& ┐(АВ), или кратко ВА, где хВ(х)- видовое понятие, а хА(х)- родовое. Когда, например, понятие хА(х) строго включено в понятие хВ(х), тогдаWхА(х)
Из названных отношений следует, что возможны четыре вида подчинения:1) совместимые и исчерпывающие - представлены модельными схемами 7 и 8; 2) несовместимые и исчерпывающие - схемы 2 и 3; 3) совместимые и неисчерпывающие - схемы 10 и 11; 4) несовместимые и неисчерпывающие - представлены модельными схемами 5 и 6.
4) Отношение равенства. Понятия хА(х) и хВ(х) находятся в отношении равенства, если объемы их совпадают: (АВ) & (ВА) при А=В, то есть, такие понятия равнообъемны.
На модельных схемах представлены три вида равенства. В первой модельной схеме А=В и их объемы пусты. Wх А(х)= Ø иWх В(х) = Ø. На 4-ой модельной схеме воспроизведено равенство для универсальных понятий, когдаWх А(х)=U1 и Wх В(х)=U2, причем так, чтоU1=U2. Символическим изображением данных отношений являются совмещенные друг с другом прямоугольные четырехугольники. В том и другом случаях имеет место отношение графического равенства. Такие понятия находятся в отношении совместимости и исчерпывания. На 9-ой модельной схеме отображено равенство классов, когда А и В не пусты и не универсальны. Они находятся в отношении совместимости и неисчерпывания.
П
ри этом родовое понятие называется подчиняющим, а видовые – соподчиненными. При оперировании соподчиненными понятиями надо иметь в виду два правила несовместимости. Первое правило: соподчиненные понятия должны быть ближайшими видами одного общего для них рода. Несоблюдение данного правила приводит к ошибке соподчинения видовых понятий, принадлежащих разным родовым понятиям. Второе правило: соподчиненные понятия не должны находится в отношении пересечения.Вторым видом отношений между несовместимыми понятиями является отношение противоположности. Два соподчиненных понятия называются противоположными(контрарными), если одно из них содержит такие признаки, которые исключает другое понятие, замещая их на противоположные. Имена таких понятий выражаются в языке антонимами. Например, «тяжелое» и «легкое», «далекое» и «близкое» и т.п. Отношение противоположности присуще таким видовым понятиям, которые находятся на крайних полюсах рода. Иллюстрацией такого положения может служить схема:
О
ба противоположных понятия «белое» (В) и «черное» (С) входят в объем подчиняющего понятия «цвет» (А), но полностью всего объема подчиняющего понятия не исчерпывают. Между противоположными понятиями существуют промежуточные виды со своими признаками. Между крайними противоположностями белого и черного цветов можно последовательно перечисляя объем средний части перейти от одного к другому, и наоборот.Третьим видом отношений между несовместимыми понятиями является отношение противоречия. Противоречащими
(контрадикторными) называются соподчиненные понятия, которые исключают друг друга и оба вместе полностью исчерпывают объем родового понятия. Отношение противоречия графически изображается так:
Н
апример, «белый» и «небелый». В отношении противоречия находятся положительные и отрицательные понятия. Оба эти понятия одновременно и в одном отношении нельзя применить к одному и тому же предмету не впадая в логическое противоречие. Древнегреческий поэт Феогнид из Мегар (VIв. до н.э.) подвел безрадостный итог совей жизни в такой контрадикторно сформулированной сентенции:«Сделав, я не сделал и не закончил, закончив;
совершив, не совершил и достигнул, не достигнув».1
Для того, чтобы отличить противоположные и противоречащие понятия, следует придерживаться двух правил: 1) противоречащие – это пара понятий, одно из которых положительное, а другое – отрицательное; противоположные понятия оба положительны; 2) противоречащие понятия оба вместе исчерпывают класс предметов, мыслимых в понятии; противоположные – не исчерпывают весь объем родового понятия.
Отношение противоречия и противоположности выполняют особую роль в логическом рассуждении. Каждое из них может достигать такой интенсивности и такого утончения, когда одно превращается в другое. Полемика об этих понятиях до сих пор не приводит к полному удовлетворению.
В ряду противоположных понятий есть такие, которые находятся в отношении бинарной оппозиции (лат. оppositio– противопоставление). Существуют три вида бинарной оппозиции. 1) Прямое противопоставление, при котором два понятия контрарны по содержанию, то есть оба являются положительными, но в своей совокупности исчерпывают весь объем родового понятия. Между содержаниями таких понятий имеет место двусторонняя импликация. Например, «правый» и «левый», «верх» и «низ», «восток» и «запад», «плюс» и «минус», «истина» и «ложь» и т.п. Один выступает антиподом другого. 2) Косвенное противопоставление (ослабленная оппозиция), при котором два понятия контрадикторны по содержанию, то есть одно из них положительное, а другое – отрицательное, но в своей совокупности они не исчерпывают всего объема родового понятия. Между содержаниями таких понятий возможна только односторонняя импликация. Например, «старый» и «нестарый». Между такими понятиями существуют промежуточные виды («зрелый», «пожилой» и т.п.). Из содержания одного («старый») не следует содержание другого («молодой»). Пример амбивалентного отношения: «любовь – ненависть». 3) Конверсная оппозиция, при которой фиксируется контраст сравниваемых понятий (оба положительные), их резкое противопоставление. Например, «лед» и «пламя», «умный» и «дурак» и т.п.
2
В свою очередь бывает, хотя и редко, ситуация, при которой соподчиненные понятия исчерпывают весь объем родового понятия и при этом не являются противоречащими. Например, «простое предложение» и «сложное предложение». Они исчерпывают все виды предложений, выделенных с указанной точки зрения.
Анализ круговых схем показывает, что попытка выдержать требование выявления отношений между двумя произвольно взятыми сравнимыми понятиями наталкивается на ряд серьезных затруднений и, прежде всего на ситуацию, принуждающую вводить третье понятие, без которого вид отношения между двумя понятиями не может быть установлен. Так, обсуждение двух соподчиненных понятий обнаруживает, что отношение соподчинения принуждает мыслить еще одно (третье) понятие, подчиняющее каждое из них. В противном случае отношение соподчинения исчезает. На круговых схемах они принимают вид несравнимых понятий, но это противоречит их смыслу, поскольку они являются ближайшими видами своего родового понятия. Данное обстоятельство приводит к необходимости введения отношения подчинения, которое, в свою очередь, не присущее несовместимым понятиям. К тому же ряд отношений между понятиями в круговых схемах просто невыразимы. Еще раз подчеркнем, что для выявления отношений между понятиями были приняты условия: 1) выявляются и анализируются отношения, присущее двум совместимым понятиям (осуществляется по парный анализ понятий); 2) для ясности и определенности возможных отношений рассматриваются только простые понятия.
Осуществим второй семантический подход для интерпретации и наглядного представления отношений между простыми понятиями, который задается модельными схемами, является их полным перечнем и снимает ряд затруднений, встречающихся в круговых схемах Эйлера. Такие модельные схемы были предложены Кейнсом в 1906 году.
Предположим, даны два понятия x A(x) иxB(x) и пусть родом первого понятия будетU, а второгоU. Если универсумы U иU2различны и в них нет ни одного совпадающего элемента, то они являются несравнимыми. Так, если два понятия, одно из которыхxА (х), скажем "мудрость" принадлежит универсумуU, а второе -x B(x), например, «голубизна», относится к универсумуU2, то объединение таких универсумов образует нелепость. В качестве подобных примеров можно привести образование универсумов, представляющих универсумы разного порядка, таких как вещи и ее части, вещи и ее свойства и т.п. Возникновение универсумов такого рода приводит к противоречиям и парадоксам. Стало быть, запрет на объединение несравнимых понятий правомерен из-за возможных противоречий образуемого из них общего универсума. Такого рода универсумы не могут совпадать между собой.
Если роды двух понятий совпадают хотя бы в единственной своей части, то имеют место сравнимые понятия. Именно о таких универсумах и отношениях, в которых могут находиться сравнимые понятия, строится новая семантика. Особенностью данной семантики является допущение пустых универсумов, то есть областей реально несуществующих объектов и, следовательно, понятий, объем которых пуст, непустых универсумов и таких универсумов, когда родовое понятие совпадает с универсумом рассуждения. Получим следующий перечень модельных схем:
..
Выделим из числа сравнимых понятий три фундаментальных отношения.
1) Отношение совместимостиимеет место тогда и только тогда, когда пересечение объемов понятий х А (х) и хB(х) не являются пустыми:
WхА(х)∩ WхВ(х)
Запись можно упростить так: А∩В ≠ Ø Отношение совместимости означает, что должен существовать хотя бы один предмет, для содержания которого было бы вернох(А(х)В(х)). На модельных схемах такому отношению соответствуют 4, 7, 8, 9, 10, 11, 12 и 15 схемы.
2) Отношение исчерпыванияимеет место тогда и только тогда, когда объединение понятий х А(х) и хВ(х) совпадает с универсумом:
Wх А(х)UWхВ(х)=U
В упрощенной записи: АUB=U. Содержание понятий, находящихся в отношении исчерпываниях(А(х)VB(х)) равно универсуму. На модельных схемах такому отношению соответствуют 2, 3, 4, 7, 8, 14 и 15 схемы.
3) Отношение включения имеет место тогда и только тогда, когда одно понятиевходит в объем другого понятия. Для двух понятий хА(х) и хВ(х) отношение включения выполняется при условии:
(WхА(х)WхВ(х))V(Wх В(х)WхА(х)).
В упрощенной записи будем иметь (АВ)V(ВА), где "" знак нестрогого включения. Для содержания этих понятий достаточно, что х (А(х)В(х)), либох(В(х)А(х)). На модельных схемах такому отношению соответствуют 5, 6, 7, 8, 10 и 11, а так же 1, 2, 3, 4 и 9 схемы как предельные случаи.
Указанные три вида отношений получили название фундаментальных в силу того, что их различные сочетания порождают все другие возможные отношения между двумя сравнимыми понятиями, образуяпроизводные отношения. Из числа таких производных отношений назовем следующие.
1) Отношение несовместимости .Два понятия хА(х) и хВ(х) находятся в отношении несовместимости, если и только если, их пересечение пусто
WхА(х)∩WхВ(х)=Ø,
или кратчайшим образом: А∩В= Ø. Их содержания отвечают требованию ┐х(А(х)&B(х)).
2) Отношение неисчерпывания. Два понятия хА(х) и хВ(х) находятся в данном отношении, если и только если их объединение не образует полного универсума
Wх А (х)UWхВ(х) ≠U,
или кратко: АUВ ≠U. Их содержания удовлетворяют условию: ┐х(А(х)VВ (х)).
3) Отношение подчинения. Понятия хА(х) и хВ(х) находятся отношении подчинения, если имеет место включения объема одного из них в объем другого. Припрямом включении объем второго понятия полностью входит в объем первого понятия. В упрощенной записи это можно указать так (АВ). Приобратномвключении понятие В находится в объеме А: (ВА).
Пустое понятие включается в любое другое понятие. Так, если из двух понятий хА(х) ихВ(х), хотя бы одно пусто, то его включение может быть записано так:
(WхА(х)= Ø)(WхА(х)WхВ(х),
или иначе: для всякого В верно, что В(ØВ).Аналогично в другом случае.
Если из двух понятий хотя бы одно является универсальным классом, то есть совпадает с униерсумом, то для х А(х) их В (х) будет верно
(Wх А (х) =U)(Wх В (х)Wх А (х)),
или иным способом записи: для всякого В верно, что (В U).
Аналогично в другом случае.
Как прямое, так и обратное включение может быть строгим или нестрогим. Отношение строгого включения характеризуется тем, что объем понятия хА(х) строго включается в объем понятия хВ(х), если выполняется условие:
(АВ) & ┐(ВА),
в кратчайшей записи АВ. В этой ситуации хА(х) есть вид, а хВ(х)- род, и где "" -знак отношения строгого включения. В другом случае , при котором второе понятие включено в объем первого, то верным будет условие: (ВА).& ┐(АВ), или кратко ВА, где хВ(х)- видовое понятие, а хА(х)- родовое. Когда, например, понятие хА(х) строго включено в понятие хВ(х), тогдаWхА(х)
Из названных отношений следует, что возможны четыре вида подчинения:1) совместимые и исчерпывающие - представлены модельными схемами 7 и 8; 2) несовместимые и исчерпывающие - схемы 2 и 3; 3) совместимые и неисчерпывающие - схемы 10 и 11; 4) несовместимые и неисчерпывающие - представлены модельными схемами 5 и 6.
4) Отношение равенства. Понятия хА(х) и хВ(х) находятся в отношении равенства, если объемы их совпадают: (АВ) & (ВА) при А=В, то есть, такие понятия равнообъемны.
На модельных схемах представлены три вида равенства. В первой модельной схеме А=В и их объемы пусты. Wх А(х)= Ø иWх В(х) = Ø. На 4-ой модельной схеме воспроизведено равенство для универсальных понятий, когдаWх А(х)=U1 и Wх В(х)=U2, причем так, чтоU1=U2. Символическим изображением данных отношений являются совмещенные друг с другом прямоугольные четырехугольники. В том и другом случаях имеет место отношение графического равенства. Такие понятия находятся в отношении совместимости и исчерпывания. На 9-ой модельной схеме отображено равенство классов, когда А и В не пусты и не универсальны. Они находятся в отношении совместимости и неисчерпывания.