Решение

Выражение (12) при λ=cоnst примет вид

.

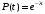Тогда:



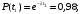
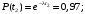
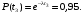
Частота отказов (7):



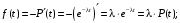
Тогда:





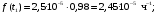
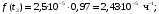
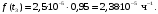
Т.к. средняя наработка на отказ – это математическое ожидание случайной наработки объекта до первого отказа, а математическое ожидание при экспоненциальном законе распределения

,

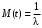то



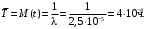
Пример 6. В течение некоторого периода времени производилось наблюдение за работой одного объекта. За весь период зарегистрированоn(t)=15 отказов. До начала наблюдений объект проработал 258 ч, к концу наблюдения наработка составила 1233 ч. Определить среднюю наработку на отказ T_o.

Решение

Наработка за указанный период составила

∆t=t₁–t₂=1233–258=975 ч.

Приняв 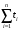= 975 ч, определим среднюю наработку на отказ по статистическим данным (14)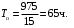



Пример 7. В аппаратуре было зафиксировано 8 отказов. Время восстановления составило: t₁ = 12 мин, t₂ = 23 мин, t₃ = 15 мин, t₄= 9 мин, t₅= 17 мин, t₆ = 28 мин, t₇ = 25 мин, t₈ = 31 мин.

Требуется определить среднее время восстановления аппаратуры t_в.

Решение

Среднее время восстановления аппаратуры (2.14)



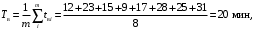
Пример 8. Аппаратура имела среднюю наработку на отказ Т_о=65 ч и среднее время восстановления Т_в=1,25 ч. Требуется определить коэффициент готовности К_г.

Решение

Коэффициент готовности (16)



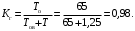
Пример 9. Известно, что интенсивность отказов λ= 0,02 ч^–1, а среднее время восстановления t_в

---

=10 ч. Требуется вычислить коэффициент готовности и функцию готовности изделия. Закон распределения экспоненциальный.

Решение

Коэффициент готовности (16)



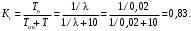
Пример 10. Определить коэффициент технического использования машины, если известно, что машину эксплуатируют в течение года Т_э=8760 ч. За этот период эксплуатации машины суммарное время восстановления отказов составило t_в=40 ч. Время проведения регламента составляет t_о=20 ч. Суммарное время, затраченное на ремонтные работы за период эксплуатации составляет 15 суток (t_р =15·24=360 ч).

Решение

Определим суммарное время наработки машины:

t_н=Т_э – (t_в+t_р+t_о)=8760 – (40+360+20)=8340.

Определим коэффициент технического использования (17)


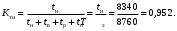
Задачи для решения

Задача 1. На испытание поставлено N₀=1500 однотипных электронных ламп. За 5000 ч отказало n(t)=100 ламп. Требуется определитьза период 3000 ч вероятность безотказной работы P(t)и вероятность отказаQ(t).

Задача 2. На испытание поставлено N₀=2000 однотипных приборов. За первые Δt₁=3000 ч отказало 100 приборов, а за интервал времени Δt₂=3000…4000 чотказало еще Δt₂=100 приборов. Требуется определить частотуf(Δt₂) и интенсивностьλ(Δt₂) отказов приборов в промежутке времени ∆t = 3000–4000 ч.

Задача 3. На испытание поставлено N₀=500 изделий. За время t=3000 ч отказало n(3000)=100 изделий, за интервал ∆t=100 ч отказало n(∆t)=50 изделий. Требуется определить вероятность безотказной работы P(t), частоту отказовf(t) и интенсивность отказовλ(t) за 3000, 3100, 3050 часов, частоту интенсивность λ(t) отказов в интервале 3000…3100 часов.

Задача 4. Три однотипных объекта поставлены на испытания. За период наблюдения было зафиксировано по первому объекту 8 отказов, по второму – 10, третьему – 8. Наработка первого объекта составила t₁=160 ч, второго t₂=300 ч, третьего t₃=240 ч. Определить наработку объектов на отказ.

Задача 5. Пусть время работы элемента до отказа подчинено экспоненциальному закону λ=2,5·10^–5 ч^–1. Требуется определить вероятность безотказной работы P(t), частоту отказов f(t) и среднюю наработку до отказа

---

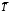при t=1000, 2000, 3000 ч.

Задача 6. В течение некоторого периода времени производилось наблюдение за работой одного объекта. За весь период зарегистрированоn(t)=10 отказов. До начала наблюдений объект проработал 258 ч, к концу наблюдения наработка составила 1000 ч. Определить среднюю наработку на отказ T_o

Задача 7. В аппаратуре было зафиксировано 10 отказов. Время восстановления составило: t₁=10 мин, t₂=20 мин, t₃=12 мин, t₄=10 мин, t₅=15 мин, t₆=25 мин, t₇=25 мин, t₈=30 мин.

Требуется определить среднее время восстановления аппаратуры t_в.

Задача 8. Аппаратура имела среднюю наработку на отказ Т_о=75 ч и среднее время восстановления t_в=1,2 ч. Требуется определить коэффициент готовности К_г.

Задача 9. Известно, что интенсивность отказов λ= 0,01 ч^–1, а среднее время восстановления t_в=5 ч. Требуется вычислить коэффициент готовности. Закон распределения экспоненциальный.

Задача 10. Определить коэффициент технического использования машины, если известно, что машину эксплуатируют в течение года Т_э=9010 ч. За этот период эксплуатации машины суммарное время восстановления отказов составило t_в=50 ч. Время проведения регламента составляет t_о=10 ч. Суммарное времяt_р, затраченное на ремонтные работы за период эксплуатации составляет 10 суток.

---

Практическая работа №3. Повышение надежности технических систем резервированием

Цель:

• 
  закрепление теоретических знаний и развитие умений расчета показателей надежности элементов ТС.
  

Задачи:

• 
  повысить надежность ТС заданными способами.
  

Основные теоретические сведения

Резервирование – метод повышения характеристик надёжности технических устройств или поддержания их на требуемом уровне посредством введения аппаратной избыточности за счет включения запасных (резервных) элементов, дополнительных по сравнению с минимально необходимым для выполнения заданных функций.

Резерв – аппаратура:

• 
  обладающая характеристиками основной;
  
• 
  исправная, готовая к включению в любой момент времени
  

Резервирование:

• 
  увеличение стоимости;
  
• 
  увеличение надежности.
  

Простейшим видом резервирования можно назвать параллельное соединение элементов (рис. 2.3).

Вероятность отказа системы с nэлементов:

Q=[q(t)]ⁿ. (18)

вероятность безотказной работы

P(t)=1−[q(t)]ⁿ. (19)

Различают схемы надежности с поканальным (рис. 1) и поэлементным резервированием (рис. 3).



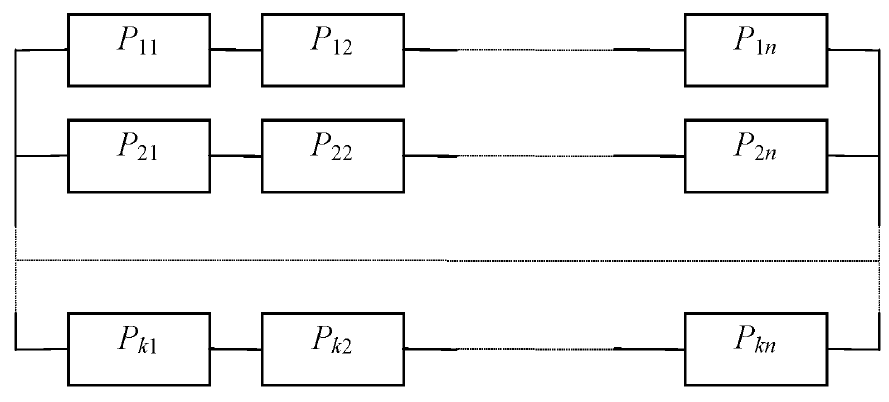
Рис. 1. Схема поканального резервирования



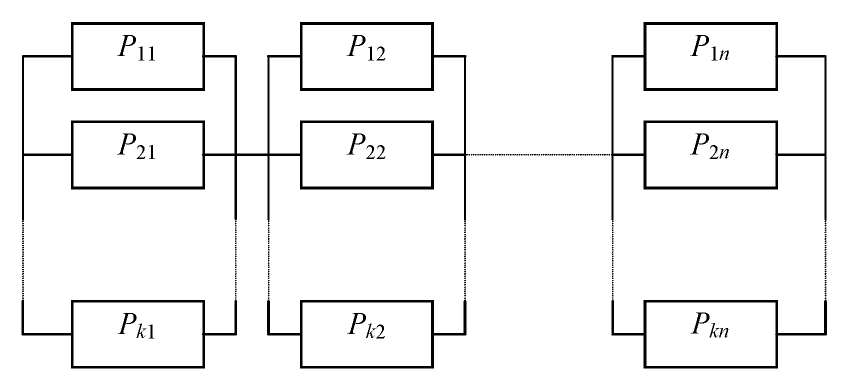
Рис. 2. Схема поэлементного резервирования

Надежность первых систем определится по формулам:

• 
  для различных элементов в цепи и каналах:
  

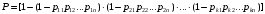; (20)

• 
  для идентичного дублирования цепи:
  

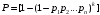; (21)

• 
  для одинаковых элементов в цепи и идентичного дублирования:
  

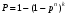. (22)

Надежность вторых систем определится по формулам:

• 
  для различных элементов в цепи и каналах:
  

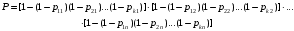; (23)

• 
  для идентичного дублирования элементов:
  

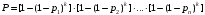; (24)

• 
  для одинаковых элементов в цепи и идентичного дублирования:
  

---

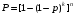. (25)

Структурные схемы надежности систем с частично-параллельным резервированием отличаются от параллельного резервирования тем, что для ее работоспособности необходимо работоспособность нескольких элементов (рис. 3).

При обозначении через р(t) вероятности исправной работы отдельного элемента, вероятность всей системы Р(t) будет иметь m исправных элементов из общего числа элементов п по биноминальному распределению (26):

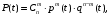(26)

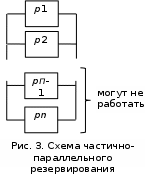где 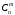– число сочетаний из n элементов по m

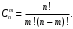(27)

Можно принять работоспособность системы при количестве элементов j и неработоспособность при количестве j–1. Тогда вероятность безотказной работы всей системы

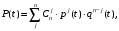(28)

где j – число исправных элементов, при котором обеспечивается работоспособность системы.

Задание

1. Дана система с последовательным соединением звеньев с вероятностью безотказной работы р_i(t) 0,970, 0,950, 0,990, 0,980, 0,980.

Определить вероятность безотказной работы всей системы Р(t).

Посредством поэлементного резервирования «слабого» звена повысить вероятность безотказной работы всей системы Р(t) до не менее 0,92: определить минимальное количество резервных элементов.

2. Дана система с последовательным соединением звеньев с вероятностью безотказной работы р_i(t) 0,970, 0,970, 0,990, 0,980, 0,980.

Определить вероятность безотказной работы всей системы Р(t).

Посредством поканального резервирования повысить вероятность безотказной работы всей системы Р

---

Смотрите также файлы

• 1. Определение элементов гладкого цилиндрического соединения с выбором средств.doc

• Основные проблемы философской антропологии.docx

• Курсовая работа тема.doc

• Октябрьская революция создала условия для полного отмирания религиозных предрассудков.docx

• Сочинение Детство это огромный край, откуда приходит каждый.docx