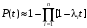Файл: Методические указания и индивидуальные задания для студентов, обучающихся по направлению 20. 03. 01 Техносферная безопасность Составитель.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.03.2024
Просмотров: 113
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(t) до не менее 0,999: определить минимальное количество резервных каналов.
3. Дана система с последовательным соединением звеньев с вероятностью безотказной работы рi(t) 0,970, 0,970, 0,990, 0,980, 0,980.
Посредством поэлементного резервирования повысить вероятность безотказной работы всей системы Р(t) до не менее 0,999: определить минимальное количество резервных элементов. Количество резервов для всех элементов взять одинаковое.
4. Определить вероятность безотказной работы системы Р(t) для частично-параллельного резервирования при:
4. ИНДИВИДУАЛЬНЫЕ ДОМАШНИЕ ЗАДАНИЯ
4.1. Общие методические указания
В соответствии с учебным графиком для студентов, обучающихся по направлению 20.03.01 «Техносферная безопасность», предусмотрено выполнение одного индивидуального домашнего задания (ИДЗ), которое должно содержать:
Выполнение этих заданий необходимо для закрепления теоретических знаний и приобретения практических навыков.
4.2. Варианты ИДЗ и методические указания
Контрольные вопросы составлены в двадцати вариантах по лекционному материалу, изложенному в презентациях. Каждый вариант включает два вопроса, приведенных в табл. 1.
Номер варианта задания определяется по последним двум цифрам номера зачетной книжки. Если образуемое ими число больше 20, то следует взять сумму этих цифр. Например, если номер зачетной книжки З-1Е50/12, то номер варианта задания равен 12. Если номер зачетной книжки З-1Е50/26, то номер варианта задания равен 8.
Таблица 1
Вопросы для выполнения контрольной работы
Построить дерево отказов для известной (по выбору) студентов простой технической системы. Вероятностью отказа элементов задаться самостоятельно.
Методические указания к решению задания 1
Дерево отказов – это модель надежности, отражающая логико-вероятностные взаимосвязи между отдельными событиями в виде первичных или результирующих отказов, совокупность которых приводит к головному событию (аварии, происшествию и т.д.)
Основной целью построения дерева отказов является символическое представление существующих в системе условий, способных вызвать головное событие. Дерево отказов позволяет также выявить слабые места технической системы.
Структура «дерева отказа» включает в себя первичные и результирующие отказы, головное событие. Для связи между событиями в узлах «деревьев» используются знаки «И» и «ИЛИ». Логический знак «И» означает, что вышестоящее событие возникает при одновременном наступлении нижестоящих событий (соответствует перемножению их вероятностей для оценки вероятности вышестоящего события). Знак «ИЛИ»означает, что вышестоящее событие может произойти вследствие возникновения одного из нижестоящих событий.
Прежде чем приступить к построению дерева отказов исследователь тщательно изучает систему. Поэтому описание технической системы должно быть частью выполнения задания.
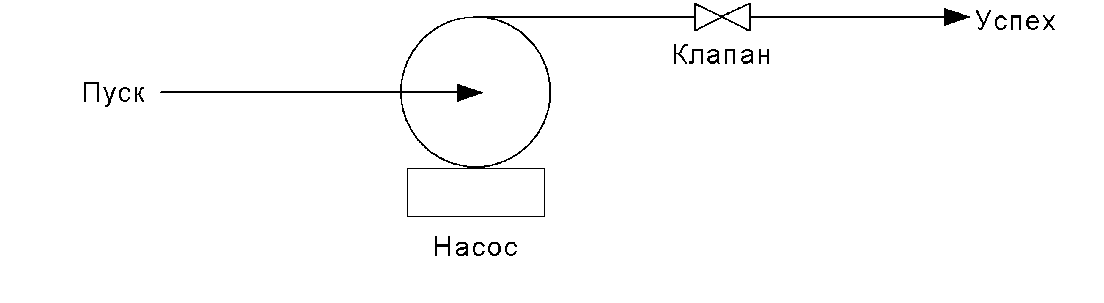
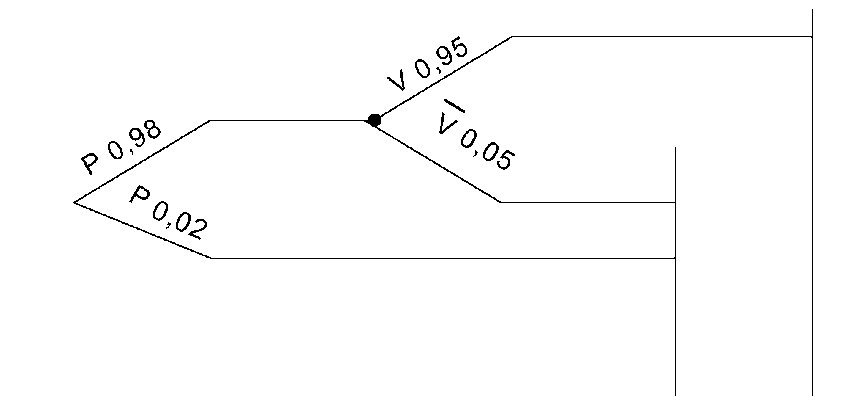
Пример. На рис. 1 показана система последовательно соединенных элементов, которая включает насос и клапан, имеющие соответственно вероятности безотказной работы 0,98 и 0,95, а также приведено дерево решений для этой системы. Согласно принятому правилу верхняя ветвь соответствует желательному варианту работы системы, а нижняя –
нежелательному. Дерево решений читается слева направо. Если насос не работает, система отказывает независимо от состояния клапана. Если насос работает, с помощью второй узловой точки изучается ситуация, работает ли клапан.
Вероятность безотказной работы системы 0,98·0,95 = 0,931. Вероятность отказа 0,98·0,05 + 0,02 = 0,069, и суммарная вероятность двух состояний системы равна единице.
а
Отказ системы Система работает
б
Рис. 1. Дерево решений для двухэлементной схемы
(работа насоса с клапаном): а – принципиальная схема; б – дерево решений
Рассчитать вероятность безотказной работы и коэффициент готовности для элементов и всей системы при заданном законе распределения для структурной схемы надежности ТС.
Номер варианта задания определяется по последним двум цифрам номера зачетной книжки. Если образуемое ими число больше 20, то следует взять сумму этих цифр. Например, если номер зачетной книжки З-1Е50/12, то номер варианта задания равен 12. Если номер зачетной книжки З-1Е50/26, то номер варианта задания равен 8.
Методические указания к решению задания 2
Техническая система состоит из большого числа подсистем, (элементов), имеющих между собой определенную взаимную связь.
Для расчета надежности системы:
По принципу функционального назначения различают системы:
При последовательном соединении (рис. 1) вероятность безотказной работы системы определяется как произведение надежностей pi подсистем
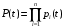 . (1)
. (1)

Рис. 1. Последовательное соединение
Для экспоненциального закона распределения
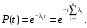 (2)
(2)
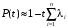 . (3)
. (3)
При параллельном соединении (рис. 2) вероятность безотказной работы системы определяется как
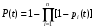 . (4)
. (4)
Для экспоненциального закона распределения
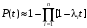
3. Дана система с последовательным соединением звеньев с вероятностью безотказной работы рi(t) 0,970, 0,970, 0,990, 0,980, 0,980.
Посредством поэлементного резервирования повысить вероятность безотказной работы всей системы Р(t) до не менее 0,999: определить минимальное количество резервных элементов. Количество резервов для всех элементов взять одинаковое.
4. Определить вероятность безотказной работы системы Р(t) для частично-параллельного резервирования при:
-
общем количестве элементов n=10; -
количестве, достаточном для работоспособности j=7; -
вероятность безотказной работы элемента p(t)=0,99.
4. ИНДИВИДУАЛЬНЫЕ ДОМАШНИЕ ЗАДАНИЯ
4.1. Общие методические указания
В соответствии с учебным графиком для студентов, обучающихся по направлению 20.03.01 «Техносферная безопасность», предусмотрено выполнение одного индивидуального домашнего задания (ИДЗ), которое должно содержать:
-
ответы на контрольные вопросы; -
выполнения задания 1 (построение дерева отказов для известной студенту простой технической системы); -
решения расчетного задания 2.
Выполнение этих заданий необходимо для закрепления теоретических знаний и приобретения практических навыков.
4.2. Варианты ИДЗ и методические указания
Контрольные вопросы
Контрольные вопросы составлены в двадцати вариантах по лекционному материалу, изложенному в презентациях. Каждый вариант включает два вопроса, приведенных в табл. 1.
Номер варианта задания определяется по последним двум цифрам номера зачетной книжки. Если образуемое ими число больше 20, то следует взять сумму этих цифр. Например, если номер зачетной книжки З-1Е50/12, то номер варианта задания равен 12. Если номер зачетной книжки З-1Е50/26, то номер варианта задания равен 8.
Таблица 1
Вопросы для выполнения контрольной работы
| Номер варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Номера вопросов | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
-
Понятия «надежность», «безопасность», -
Понятия «долговечность», «безотказность», «ремонтопригодность», «сохраняемость». -
Понятия «техника», «техническая система». -
Понятие «риск». -
Понятие «отказ», «работоспособное состояние» -
Виды отказов. -
Понятия «наработка до отказа», «ресурс». -
Понятие «авария», «техногенная чрезвычайная ситуация». -
Понятия «вероятность отказа» и «вероятность безотказной работы». -
Понятия «исправное состояние», «неисправное состояние». -
Понятия «работоспособное состояние», «неработоспособное состояние». -
Понятия «техническое обслуживание», «восстановление», «ремонт». -
Что характеризует коэффициент готовности и коэффициент технического использования? -
Понятия «восстанавливаемый объект», «невосстанавливаемый объект». -
Нарисуйте кривую интенсивности отказов. Дайте пояснения. -
Понятия «коэффициент технического использования». -
Расчет коэффициента технического использования. -
Понятие «коэффициент готовности». -
Расчет коэффициента готовности. -
Вероятность безотказной работы. -
Понятие «резервирование». -
Понятие «резерв». -
Понятие «основной элемент». -
Понятие «резервируемый элемент». -
Понятие «резервный элемент». -
Кратность резерва. -
Понятие «дублирования». -
Понятие «холодный резерв». -
Понятие «горячий резерв». -
Понятие «ненагруженный резерв». -
Понятие «поканальное резервирование». -
Понятие «поэлементное резервирование». -
Приведете мероприятия по формированию норм надежности. -
Конструктивные методы обеспечения надежности: характеристика. -
Экономические обеспечения надежности: характеристика. -
Эксплуатационные методы обеспечения надежности. -
Метод анализа опасностей: «Что будет, если..?». -
Метод анализа опасностей: «Проверочный лист». -
Метод анализа «дерево отказов». -
Метод анализа «дерево событий».
Расчетные задания
Задание 1
Построить дерево отказов для известной (по выбору) студентов простой технической системы. Вероятностью отказа элементов задаться самостоятельно.
Методические указания к решению задания 1
Дерево отказов – это модель надежности, отражающая логико-вероятностные взаимосвязи между отдельными событиями в виде первичных или результирующих отказов, совокупность которых приводит к головному событию (аварии, происшествию и т.д.)
Основной целью построения дерева отказов является символическое представление существующих в системе условий, способных вызвать головное событие. Дерево отказов позволяет также выявить слабые места технической системы.
Структура «дерева отказа» включает в себя первичные и результирующие отказы, головное событие. Для связи между событиями в узлах «деревьев» используются знаки «И» и «ИЛИ». Логический знак «И» означает, что вышестоящее событие возникает при одновременном наступлении нижестоящих событий (соответствует перемножению их вероятностей для оценки вероятности вышестоящего события). Знак «ИЛИ»означает, что вышестоящее событие может произойти вследствие возникновения одного из нижестоящих событий.
Прежде чем приступить к построению дерева отказов исследователь тщательно изучает систему. Поэтому описание технической системы должно быть частью выполнения задания.
Пример. На рис. 1 показана система последовательно соединенных элементов, которая включает насос и клапан, имеющие соответственно вероятности безотказной работы 0,98 и 0,95, а также приведено дерево решений для этой системы. Согласно принятому правилу верхняя ветвь соответствует желательному варианту работы системы, а нижняя –
нежелательному. Дерево решений читается слева направо. Если насос не работает, система отказывает независимо от состояния клапана. Если насос работает, с помощью второй узловой точки изучается ситуация, работает ли клапан.
Вероятность безотказной работы системы 0,98·0,95 = 0,931. Вероятность отказа 0,98·0,05 + 0,02 = 0,069, и суммарная вероятность двух состояний системы равна единице.

а

Отказ системы Система работает
б
Рис. 1. Дерево решений для двухэлементной схемы
(работа насоса с клапаном): а – принципиальная схема; б – дерево решений
Задание 2
Рассчитать вероятность безотказной работы и коэффициент готовности для элементов и всей системы при заданном законе распределения для структурной схемы надежности ТС.
Номер варианта задания определяется по последним двум цифрам номера зачетной книжки. Если образуемое ими число больше 20, то следует взять сумму этих цифр. Например, если номер зачетной книжки З-1Е50/12, то номер варианта задания равен 12. Если номер зачетной книжки З-1Е50/26, то номер варианта задания равен 8.
Методические указания к решению задания 2
Техническая система состоит из большого числа подсистем, (элементов), имеющих между собой определенную взаимную связь.
Для расчета надежности системы:
-
устанавливают последовательность включения отдельных подсистем; -
составляют функциональную схему работы системы во времени при выполнении поставленной задачи; -
надежность системы рассчитывают в каждом интервале времени, в котором задействованы определенные подсистемы.
По принципу функционального назначения различают системы:
-
последовательные; -
параллельные; -
со смешанным соединением.
При последовательном соединении (рис. 1) вероятность безотказной работы системы определяется как произведение надежностей pi подсистем
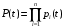 . (1)
. (1)
Рис. 1. Последовательное соединение
Для экспоненциального закона распределения
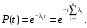 (2)
(2)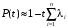 . (3)
. (3)При параллельном соединении (рис. 2) вероятность безотказной работы системы определяется как
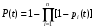 . (4)
. (4)Для экспоненциального закона распределения