Контрольная работа

Задача 19. Определить относительную плотность нефтепродукта 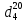по его относительной плотности .

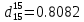Решение:

Для решения задачи воспользуемся уравнением:



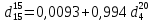
вычислим :


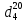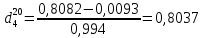
Задача 49. Относительная плотность нефтепродукта 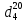= 0,725. Найти его относительную плотность при 75 ⁰С двумя способами.

Решение:

Температурная зависимость плотности нефтей и нефтепродуктов описывается уравнениями

- Д. И. Менделеева (в интервале температур от 0 до 150 ⁰С)



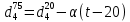
где α - средняя температурная поправка на 1 ⁰С, которая вычисляется по формуле:







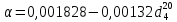
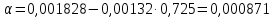
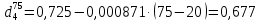
или по уравнению Мановяна:




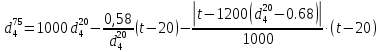
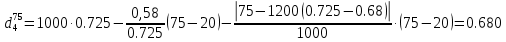
Задача 79. Определить абсолютную плотность газа гидрокрекинга при 350 ⁰С и 900 мм рт. ст., если его молекулярная масса равна 35.

Решение:

По уравнению:


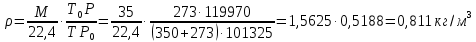
Задача 109.

Смесь узких нефтяных фракций содержит 3 компонента, содержания которых равны соответственно (% об.) 30, 30 и 40. Плотности их 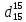равны соответственно 0,8117; 0,8202 и 0,8301. Найти относительную плотность смеси .

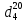Решение:

Средняя относительная плотность смеси жидких компонентов определяется по правилу аддитивности:



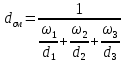
где d₁, d₂, d₃ - относительные плотности компонентов смеси;

ω₁, ω₂, ω₃ - объёмные доли компонентов.

Для решения задачи воспользуемся уравнением:

---

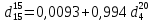
вычислим для трех плотностей:








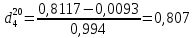
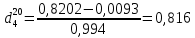
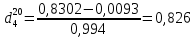
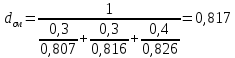
Задача 139. Вычислить среднюю молекулярную массу нефтяных фракций, имеющих средние температуры кипения 60, 138 и 165. Вычислить среднюю молекулярную массу нефтяной фракции, имеющей плотность = 0,712.

Решение:

Воспользуемся уравнением Войнова:



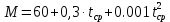
Вычислим среднюю температуру:



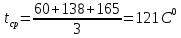
Тогда молекулярная масса



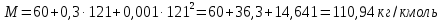
По уравнению Бриджимана:




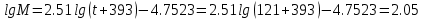
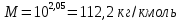
Задача 169. Определить среднюю молекулярную массу нефтепродукта, имеющего среднюю температуру кипения 250 ⁰С и характеризующий фактор

10,8. Задачу решить двумя способами.

Решение:

Для нефтяных фракций с введением характеризующего фактора применима формула Войнова-Эйгенсона:



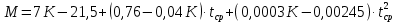
Подставляем в формулу известные величины и вычисляем молекулярную массу:



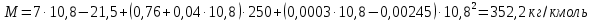
Задача 199. Смесь состоит из 21 кг н-гексана, 19 кг н-гептана и 25 кг н-октана.

Определить среднюю молекулярную массу смеси.

Решение:

Вычислить количество молей веществ для н-гексана:



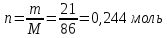
Количество молей веществ для н-гептана:



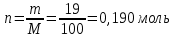
Количество молей веществ для н-октана:



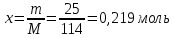
Молекулярная масса смеси по формуле равна:


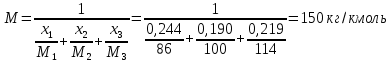
Задача 229. Определить поверхностное натяжение при 20 ⁰С нефтяной фракции 194 – 208 ⁰С, имеющей плотность

---

= 0,8031. Задачу решить двумя

способами.

Решение:

1 способ: Поверхностное натяжение нефтепродуктов (Н/м) с относительной плотностью = 0,60 - 0,92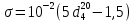




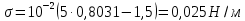
2 способ.

Определим молекулярную массу по уравнению Бриджимана:



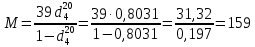
По уравнению:


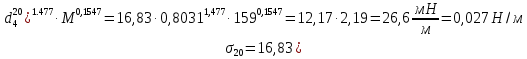
Задача 259. Кинематическая вязкость узкой нефтяной фракции при 20 ⁰С равна

32,6 сСт, относительная плотность = 0,8706. Определить динамическую и условную вязкость при той же температуре.

Решение:

Переход между кинематической и динамической вязкостью производится по преобразованному уравнению:



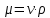
в котором все параметры должны быть определены при одной температуре.

Подставляем значения в формулу и вычисляем:



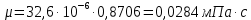
Т.к. ???? <120 мм²/с (сСт), то для перехода к условной вязкости воспользуемся преобразованным уравнением:





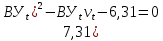
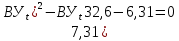
решая которое как квадратное, найдем значение условной вязкости при 20 ⁰С.

В результате решения имеем 2 корня: (0; 5,323). Корень 0 не удовлетворяет физическому смыслу задачи, поэтому условная вязкость при 20 С равна ВУ 5,323.
Задача 289. Кинематическая вязкость узкой нефтяной фракции при 50 ⁰С равна

14,00 сСт, а при 100 ⁰С – 3,78 сСт. Определить кинематическую вязкость этой фракции при 87 ⁰С. Задачу решить двумя способами.

Решение:

Воспользуемся формулой Гросса:



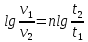
Для расчетов с её использованием сначала по двум имеющимся парам значений температура-вязкость вычислим значение коэффициента n:



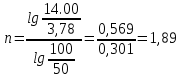
Далее, используя одну из имеющихся пар значений температура-вязкость и заданную температуру, определим вязкость при заданной температуре:

---

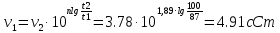
Решим эту же задачу с помощью уравнения Вальтера:



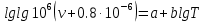
Расчет коэффициентов a и b производится по уравнениям:









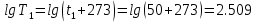
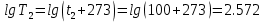
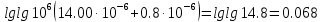
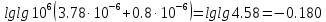
Коэффициент b:



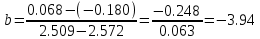
Коэффициент a:



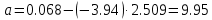
Таким образом, температурная зависимость вязкости нефтяной фракции имеет вид:



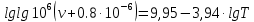
При 87 ⁰С правая часть уравнения равна:







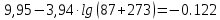
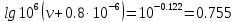
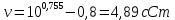
Задача 319. Кинематическая вязкость узкой нефтяной фракции при атмосферном давлении v₂₀ = 96,29 сСт. Определить вязкость фракции при той же температуре и 1,72 кгс/см².

Решение:

Зависимость вязкости от давления описывается уравнением Манстона. Вязкость (сСт) при повышенном давлении вычислим по преобразованному уравнению Манстона:


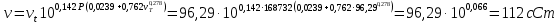
Задача 349. Определить вязкость смеси, состоящей из 47 % (масс.) фракции с вязкостью 90 сСт и 53 % (масс.) фракции с вязкостью 180 сСт.

Решение:

Для расчета вязкости смеси воспользуемся уравнением:










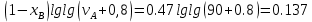
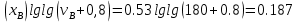
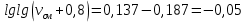
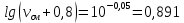
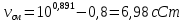
Задача 379. Определить кинематическую и динамическую вязкость неопентана при 245 ⁰С и атмосферном давлении; при 245 ⁰С и 5,2 атм.

Решение:

Вязкость паров неопентана при нормальных условиях определим по уравнению:



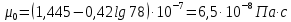
Критические параметры для бензола найдем в таблице

---

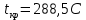
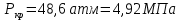
Вычислим приведенные параметры:




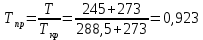
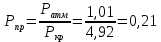
Воспользуемся номограммой, представленной на рисунке 5.3. На шкале 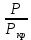отмечаем точку 0,021; на шкале 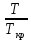- точку 0,923. Через две точки проводим прямую до пересечения со шкалой 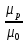- она соответствует значению1,2.

То есть

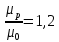
тогда



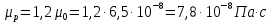
При давлении Р=5,2 атм =




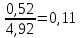
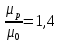
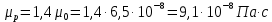
Задача 409. Разгонка по Энглеру фракции 70 – 200 ⁰С минчимкинской нефти дает следующие результаты:

Объем выкипания, % об	н.к	10	50	90
Температура, 0С	78	88	136	181

Определить СМТК, СВТК, СКТК и СУТК.

Решение:

Построим график разгонки по Энглеру.

t=f(V)



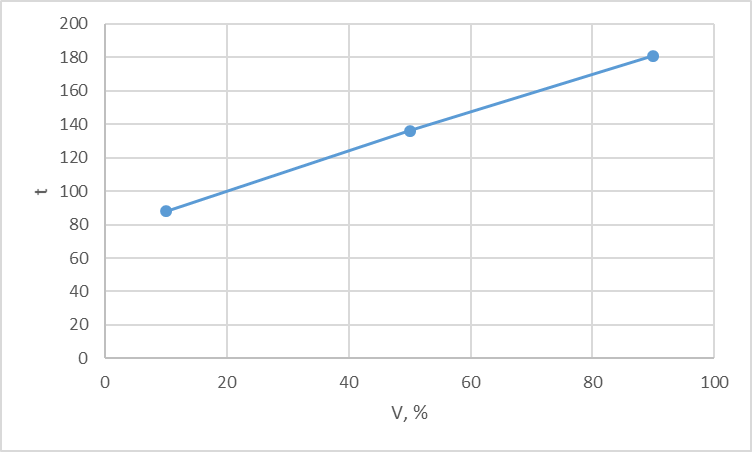
По исходным данным определяем температуру 50 % выкипания по Энглеру



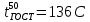
Температурную разность вычисляем по формуле:



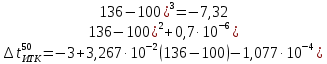
Температура 50 % выкипания по ИТК определяется по формуле:



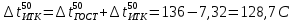
Задача 439. Определить координаты кривой ИТК по известной кривой разгонки на аппарате Энглера фракции 28 – 170 ⁰C орловской нефти ( 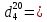0,7709)

Объем выкипания, % об	н.к	10	50	90
Температура, 0С	63	102	140	161

---

Смотрите также файлы

• Клапанные пороки сердца этиология.doc

• Аритмии клиника, экг, пульс. Экг при миокардитах, перикардитах, легочном сердце.doc

• Контрольная работа по дисциплине Приборное оборудование самолётов.pdf

• Суммативное оценивание за радел Основы Геоэкономики Ф. И. ученика Класс 11.docx

• ВОПРОСЫ к курсовому экзамену.pdf