Решение:

Построим график разгонки по Энглеру.

t=f(V)



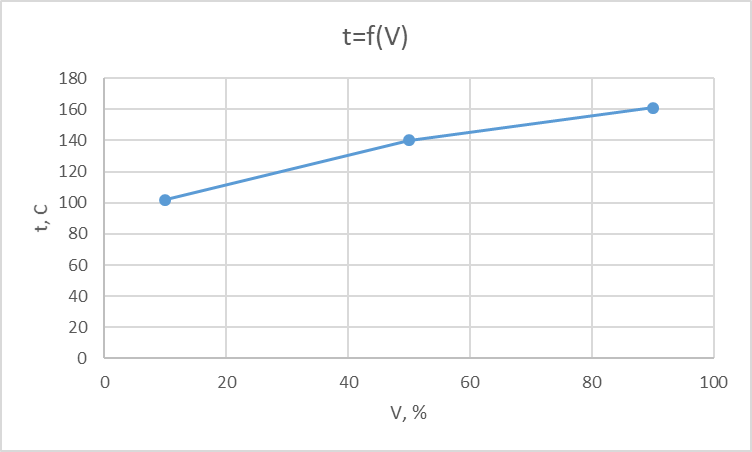
Составим новую таблицу, в которую внесем точки 0, 10, 30, 50, 70, 90 % (интерполяция недостающих значений 30 и 70 % по графику) выкипания и температуры им соответствующие.

Объем выкипания, % об	н.к	10	30	50	70	90
Температура, 0С	63	102	120	140	150	161

По исходным данным определяем температуру 50 % выкипания по Энглеру



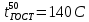
Температурную разность вычисляем по формуле:



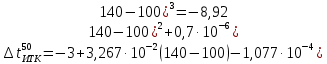
Температура 50 % выкипания по ИТК определяется по формуле:



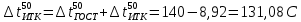
Вычисление величин 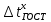производится следующим образом. От каждой последующей температуры отнимается предыдущая. Вычисления заносятся в таблицу, напротив 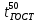ставится прочерк.

Далее для каждого значения 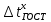путем решения уравнения отыскивается значение 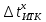(коэффициенты уравнения берутся из таблицы для каждого интервала отгона). Значения 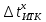заносятся в таблицу причем, соответствующие отгону до 50 % со знаком «минус», а соответствующие отгону свыше 50 % с сохранением положительного значения. Для отгона 50 %

заносится ранее определенное .

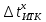Рассмотрим подробно решение уравнения для интервала 0 – 10 %.

Используя коээфициенты из таблицы, получим общий вид уравнения:



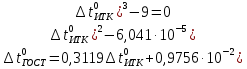
Для упрощения вида уравнения обозначим

---

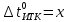
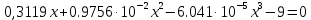
Для решения полученного уравнения применим графический метод.

Составим таблицу значений функции



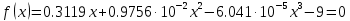
задаваясь значениями x в интервале 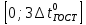целых чисел.

x	f(x)	x	f(x)	x	f(x)
0	-9,00	10	-4,97	20	0,66
1	-8,68	11	-4,47	21	1,29
2	-8,34	12	-3,96	22	1,94
3	-7,98	13	-3,43	23	2,60
4	-7,60	14	-2,89	24	3,27
5	-7,20	15	-2,33	25	3,95
6	-6,79	16	-1,76	26	4,64
7	-6,36	17	-1,18	27	5,34
8	-5,91	18	-0,58
9	-5,45	19	0,03

По данным полученной таблицы строим график



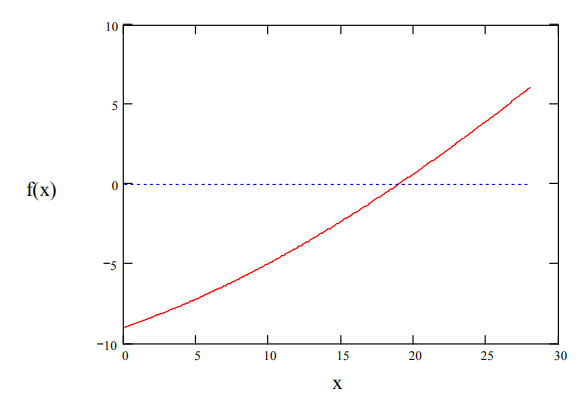
и находим абсциссу точки пересечения кривой с осью абсцисс. Эта точка и есть искомый корень уравнения. В данном случае

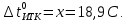
Задача 469. Определить теплоемкость жидкого нефтепродукта плотностью 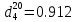при температуре 105

---

⁰С. Задачу решить двумя способами.

Решение:

Перейдем к 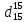по уравнению: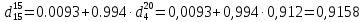



По уравнению Крэга:

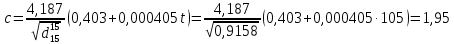
По уравнению:



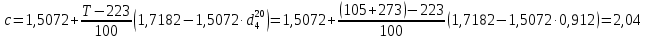
По номограмме, изображенной на рисунке при 105 ⁰С и = 0,912 по шкале для жидкости с=2,1 кДж/кгК.
Задача 499. Определить теплоемкость нефтяной фракции, имеющей t_ср = 240 ⁰С и 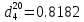, при 125 ⁰С.

Решение:

Перейдем к плотности 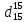по уравнению: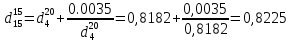



Допустим, что t_{ср куб} = t_ср, тогда характеризующий фактор Ватсона по уравнению:



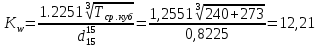
По уравнению Фаллона-Ватсона:


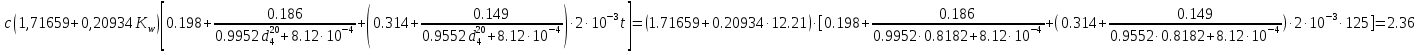
Задача 529. Определить теплоемкость паров нефтепродукта плотностью 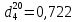при 265 ⁰С и атмосферном давлении. Задачу решить двумяспособами.

Решение:

Перейдем к плотности 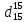по уравнению: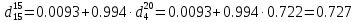



Воспользуемся формулой Бальке и Кей:



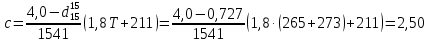
По номограмме, изображенной на рисунке при 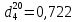по шкале паров и 265 ⁰С.

с=2,0 кДж/(кг·К).
Задача 559. Определить при 270 ⁰С и 5,5 атм теплоемкость паров нефтепродукта, имеющего 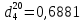, t_кр = 215 ⁰С, P_кр = 32 атм и K =12,0.

Решение:

Перейдем к плотности 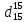по уравнению: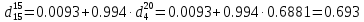



Воспользуемся формулой Бальке и Кей:



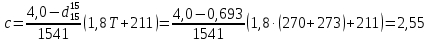
Вычислим приведенные температуру и давление:

---

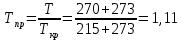
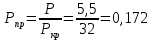
По графику, изображенному на рисунке определим поправку к теплоемкости на давление:

∆с=4,0 кДж/кмольК

Молярную массу фракции найдем по формуле Крэга:



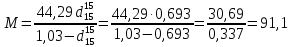
Пересчитаем поправку с мольной размерности на массовую:



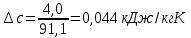
Таким образом, теплоемкость паров под давлением равна:


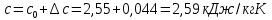
Задача 589. Определить теплоемкость смеси, состоящей из 25 кг нефтепродукта теплоемкостью 2,41 кДж/(кг·К) и 27 кг нефтепродукта теплоемкостью 0,537 ккал/(кг·К).

Решение:

Вычислим массу смеси m_см=25+27=52 кг

Следовательно, массовые доли равны:

                       = 25 / 52 = 0,48;

                    = 27 / 52 = 0,52.

0,537 ккал/(кг·К) ·4,184 = 2,25 кДж/(кг·К)

1 ккал - 4,184 кДж

Найдем теплоёмкость смеси по формуле:


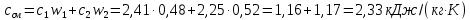
Задача 619. Определить теплоту испарения нефтяной фракции, имеющей t_ср.мол=123 ⁰С и 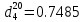при атмосферном давлении. Задачу решить двумя способами.

Решение:

По уравнению Кистяковского теплота испарения (кДж/кмоль) равна:



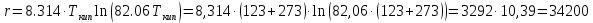
Мольную массу фракции определим по формуле Войнова:



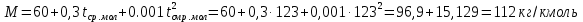
Тогда, вычисленная по уравнению Кистяковского теплота испарения (кДж/кг) равна:



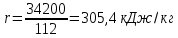
Перейдем к относительной плотности 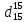по уравнению: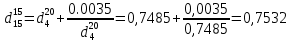



Тогда по уравнению Уэйра и Итона теплота испарения (кДж/кг) равна:



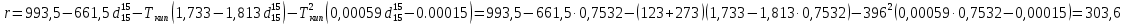
Характеризующий фактор вычислим по уравнению:


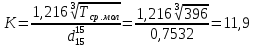
По графику, представленному на рисунке 10.2, теплота испарения равна:

---

r = 3,08 кДж/кг.
Задача 649. Определить теплоту испарения циклопентана при 2,4 атм.

Решение:

1 атм=0,1 МПа

2,4 атм = 0,24 МПа

По справочным данным определим, что нормальная температура кипения циклопентана равна 49 ⁰С.

Вычислим значение комплекса



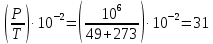
Используя график, изображены на рисунке 10.1, по кривой для углеводородов определим:



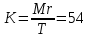
откуда


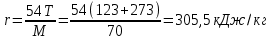
Задача 679. Определить энтальпию жидкой нефтяной фракции, имеющей

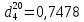, при 65 ⁰С.

Решение:

Перейдем к относительной плотности 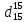по уравнению: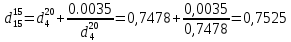



По уравнению Фортча и Уитмена:



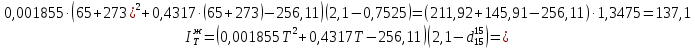
По уравнению Крэга:

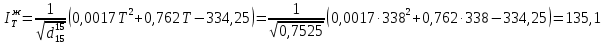
Задача 709. Определить энтальпию паров нефтепродукта плотностью 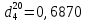при 140 ⁰С и атмосферном давлении.

Решение:

Перейдем к относительной плотности 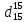по уравнению: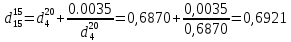



По уравнению:



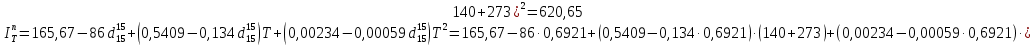
По уравнению:


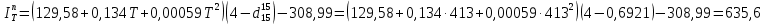
Задача 739. Определить энтальпию паров нефтяной фракции, имеющей 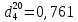, t_ср =109 ⁰С, t_кр = 295 ⁰С, P_кр = 25,5 атм, при 190 ⁰С и 4,1 кгс/см².

Решение:

4,1 кгс/см²=0,402 МПа

Перейдем к относительной плотности 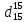по уравнению: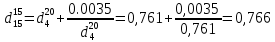



Энтальпию паров при атмосферном давлении найдем по уравнению:


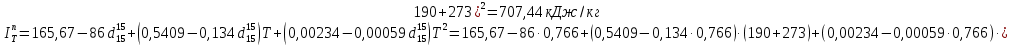
Вычислим приведенные параметры:

---

Смотрите также файлы

• Клапанные пороки сердца этиология.doc

• Аритмии клиника, экг, пульс. Экг при миокардитах, перикардитах, легочном сердце.doc

• Контрольная работа по дисциплине Приборное оборудование самолётов.pdf

• Суммативное оценивание за радел Основы Геоэкономики Ф. И. ученика Класс 11.docx

• ВОПРОСЫ к курсовому экзамену.pdf