Файл: Задача 1 по дисциплине Основы строительной механики Тема работы Расчет статически неопределимой рамы на прочность студент гр. Агс202.docx
Добавлен: 20.03.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ
Расчётно-графическая задача №1
по дисциплине Основы строительной механики
Тема работы: Расчет статически неопределимой рамы на прочность
Выполнил: студент гр. АГС-20-2 ________________/Сахапова Л.А./
Оценка: ______________
Дата: ________________
Проверил: профессор каф. механики ______________/Насонов М.Ю./
Санкт-Петербург
2022
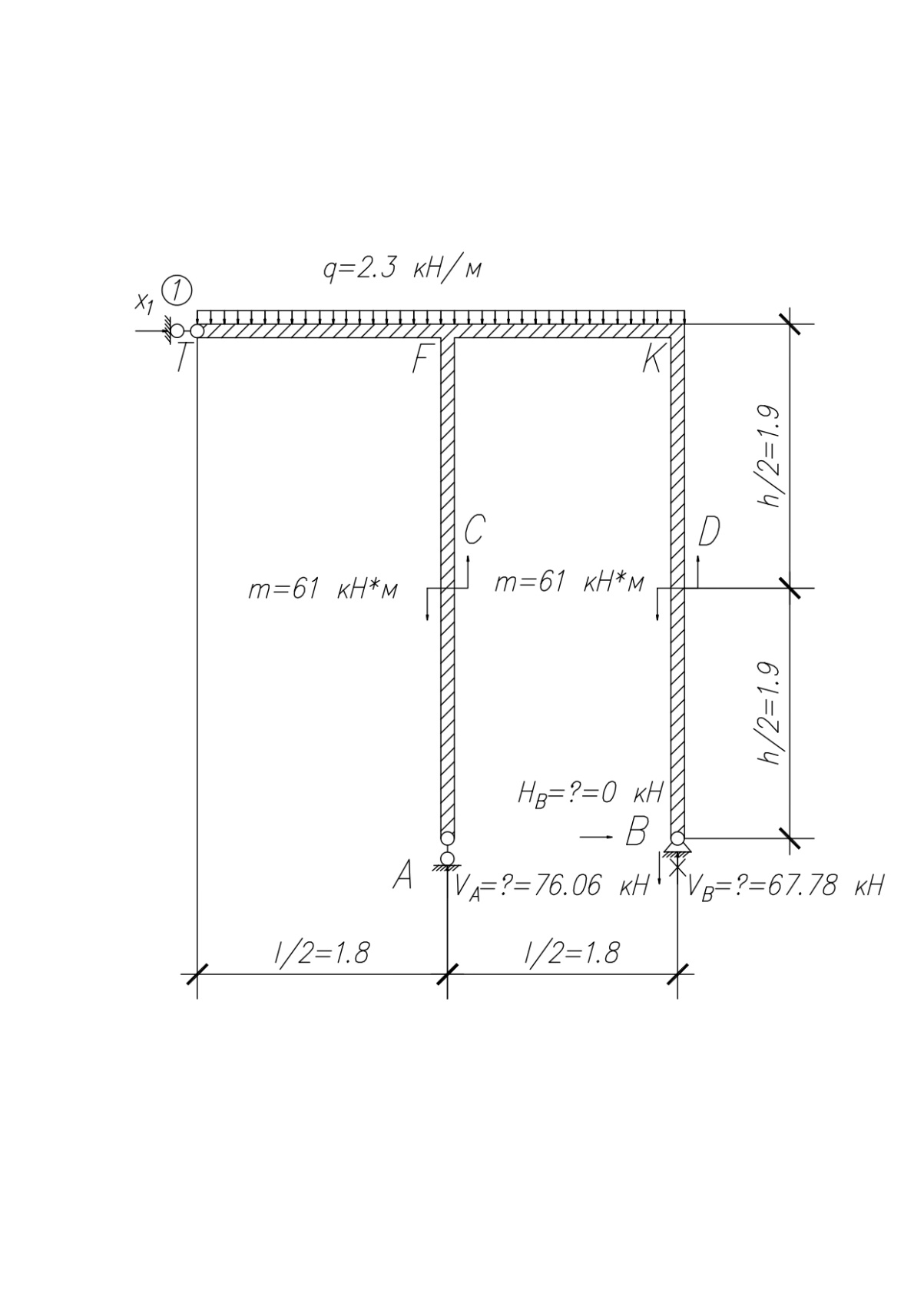 Дано: см. рис.
Дано: см. рис.Материал: сталь ВСТ3СП5
R = 240 МПа
Задание:
Подобрать двутавровое сечение, исходя из условий прочности
Решение:
-
Раскрытие статической неопределимости рамы
А. Предварительные действия
-
Определим степень статической неопределимости рамы
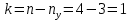
 Степень статической неопределимости рамы равна 1
Степень статической неопределимости рамы равна 1Для того, чтобы найти силу x1 необходимо к 3 уравнениям статики добавить 1 уравнение совместности деформации
-
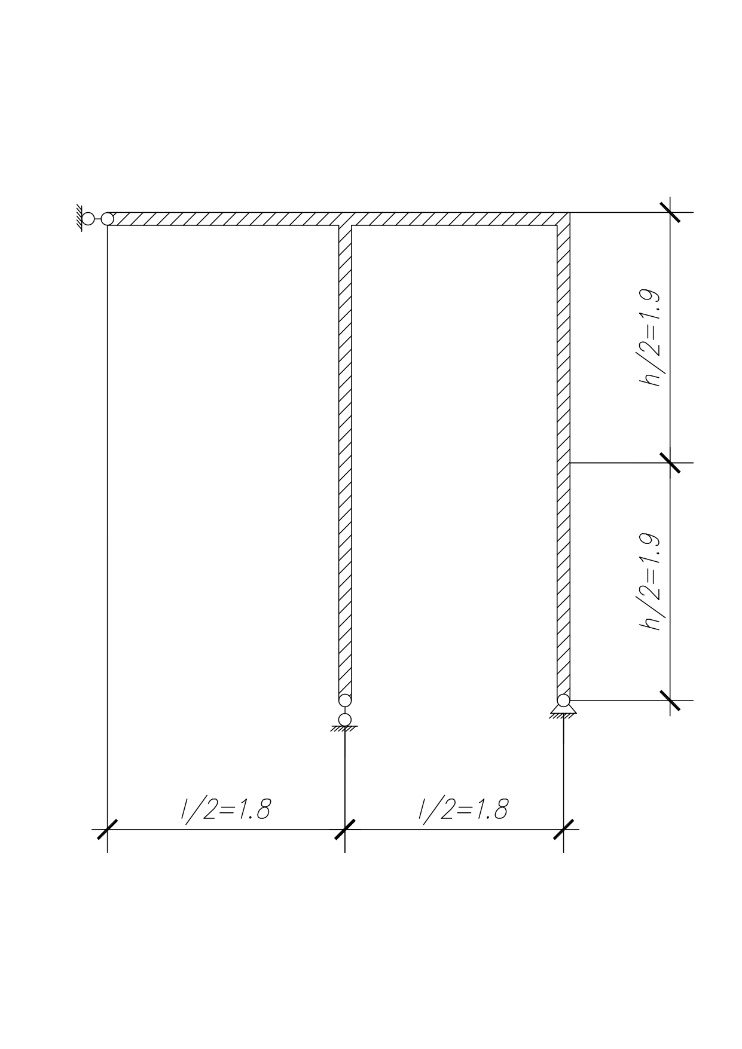
Создадим основную систему -
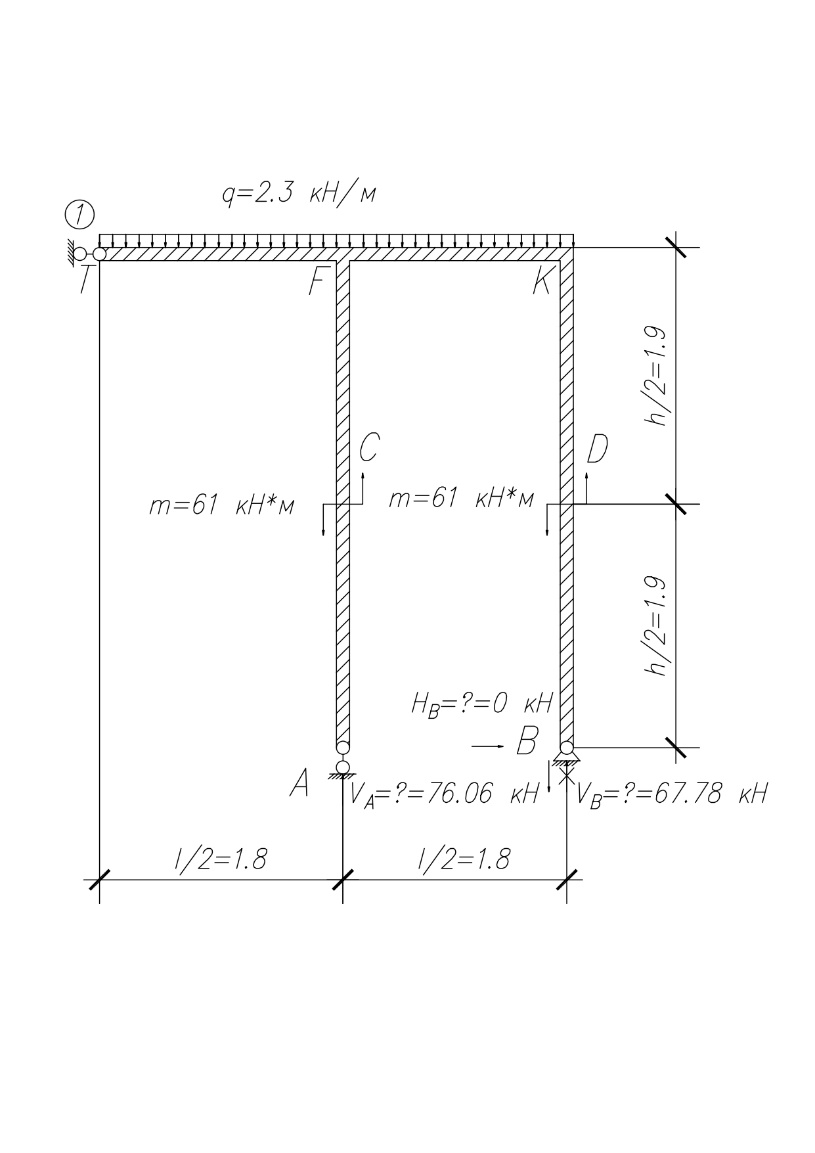 Создадим эквивалентную систему
Создадим эквивалентную систему
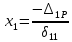
Б. Определим перемещение 1 точки от внешней нагрузки
1. Определим опорные реакции
а) ∑x = 0 → HB →+ тм ←–
HB – 4.4q = 0
HB – 30.8 = 0
HB = 30.8 кН ⊕
б) Определим опорную реакцию V
A
∑mB = 0 → VA +⟲ тм ⟳ –
- VA * 4.4 + P *2.2 + q * 4.4 * 2.2 +q* 4.4 * 2.2 = 0
- VA * 4.4 + 20 *2.2 + 7 * 4.4 * 2.2 +7* 4.4 * 2.2 = 0
VA = + 40.8 кН ⊕
в) Определим опорную реакцию VB
∑mA = 0 → VB +⟲ тм ⟳ –
+ VB * 4.4 + HB * 2.2 – P * 2.2 – q * 4.4 * 2.2 = 0
+ VB * 4.4 + 30.8 * 2.2 – 20 *2.2 – 7 *4.4 * 2.2 = 0
VB = 10 кН ⊕
г) Выполним проверку Ⅰ
∑y = 0 ↑+ тм ↓–
– P – q * 4.4 + VB + VA = – 20 – 7 * 4.4 + 40.8 + 10 = 0
д) Выполним проверку ⅠⅠ
∑mM = 0 +⟲ тм ⟳ –
– VA *3.3 + P * 1.1 + q *4.4 *1.1 – HB *2.2 + VB *1.1 = 0
– 40.8 *3.3 + 20 * 1.1 + 7 *4.4 *1.1 – 30.8 *2.2 + 10 *1.1 = 0
0 = 0
2. Построим эпюры QP и MP
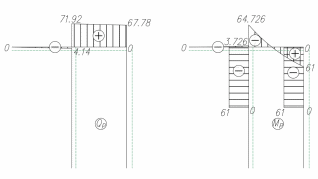
3. Проверим правильность построения эпюры MP по методу вырезания узлов
Узел C
∑mF = 0 +⟲ тм ⟳ –
+
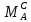 -
- 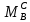 +
+ 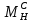 = – 15,4 + 15,4 + 0 = 0
= – 15,4 + 15,4 + 0 = 0Вывод: узел C находится в статическом равновесии
-
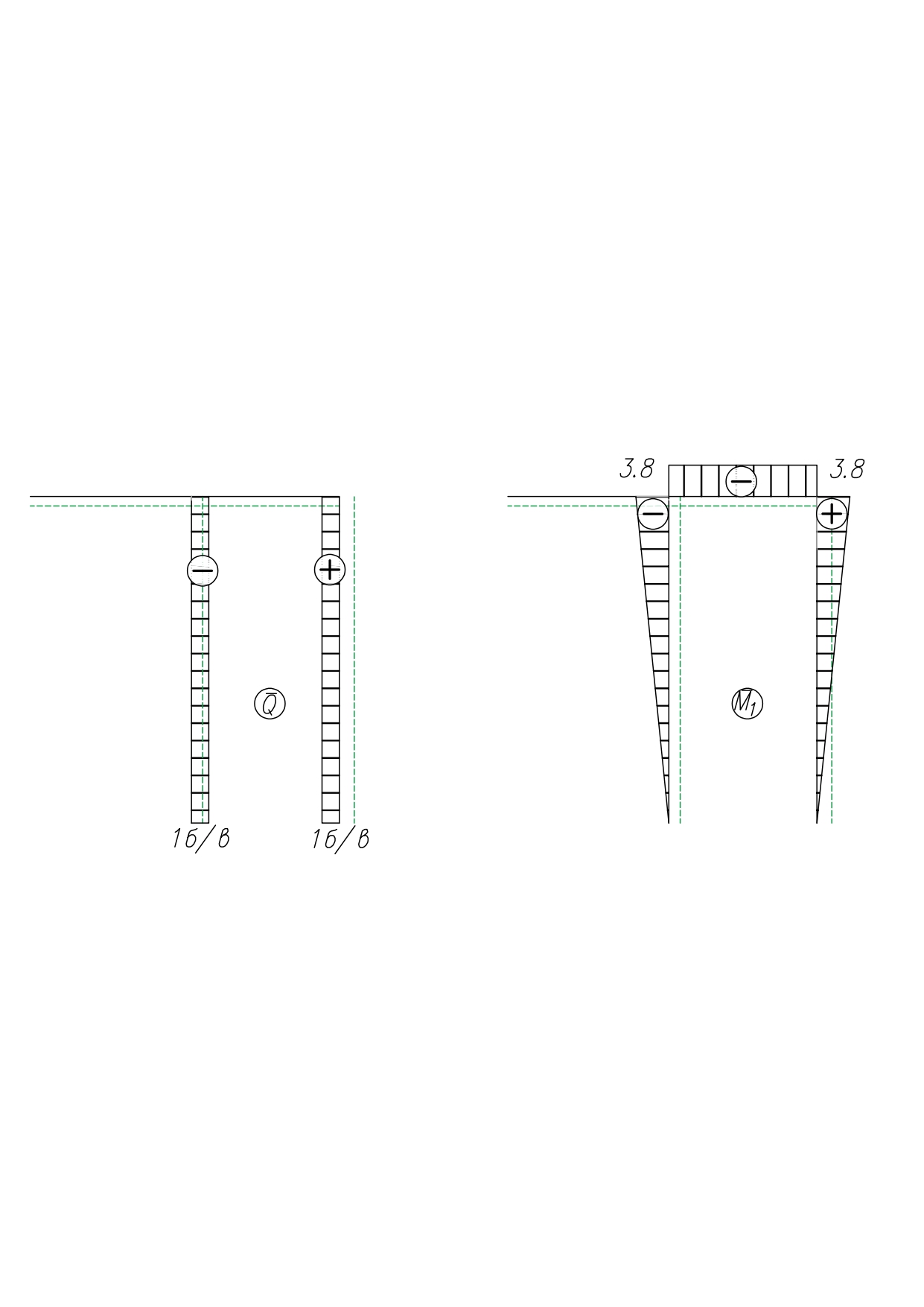 Построим эпюры Q и M от единичной нагрузки
Построим эпюры Q и M от единичной нагрузки
а) Определим опорные реакции
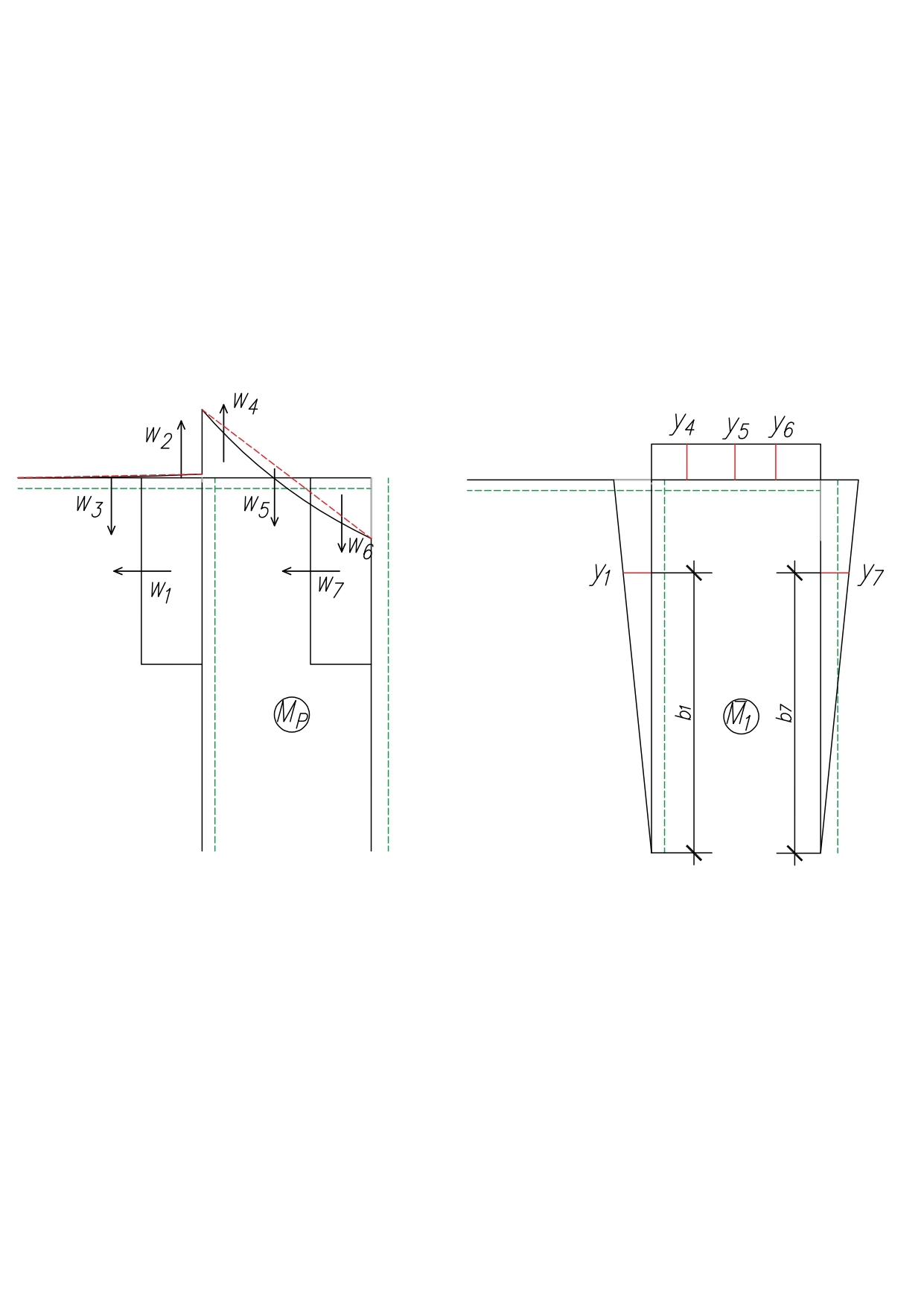 б) Построим эпюры Q и M
б) Построим эпюры Q и M -
Определим перемещение точки 1 от внешней нагрузки
а) Определим площади простых фигур
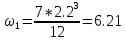 кН*м2 =
кН*м2 = 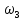 =
= 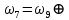
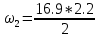 = 18.59 кН*м2 ⊖
= 18.59 кН*м2 ⊖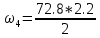 = 80.08 кН*м2 ⊕
= 80.08 кН*м2 ⊕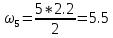 кН*м2 ⊕
кН*м2 ⊕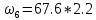 = 149.16 кН*м2 ⊕
= 149.16 кН*м2 ⊕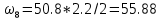
кН*м2 ⊕
б) Определим ординаты единичной эпюры
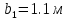 м ⊕
м ⊕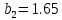 м ⊕
м ⊕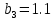 м ⊖
м ⊖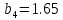 м ⊖
м ⊖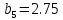 м ⊖
м ⊖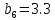 м ⊖
м ⊖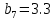 м ⊖
м ⊖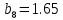 м ⊕
м ⊕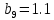 м ⊕
м ⊕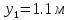 м ⊕
м ⊕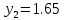 м ⊕
м ⊕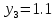 м ⊖
м ⊖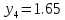 м ⊖
м ⊖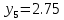 м ⊖
м ⊖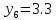 м ⊖
м ⊖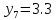 м ⊖
м ⊖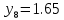 м ⊕
м ⊕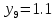 м ⊕
м ⊕в) Определим перемещение точки 1
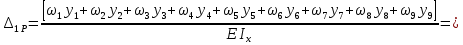
=
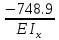
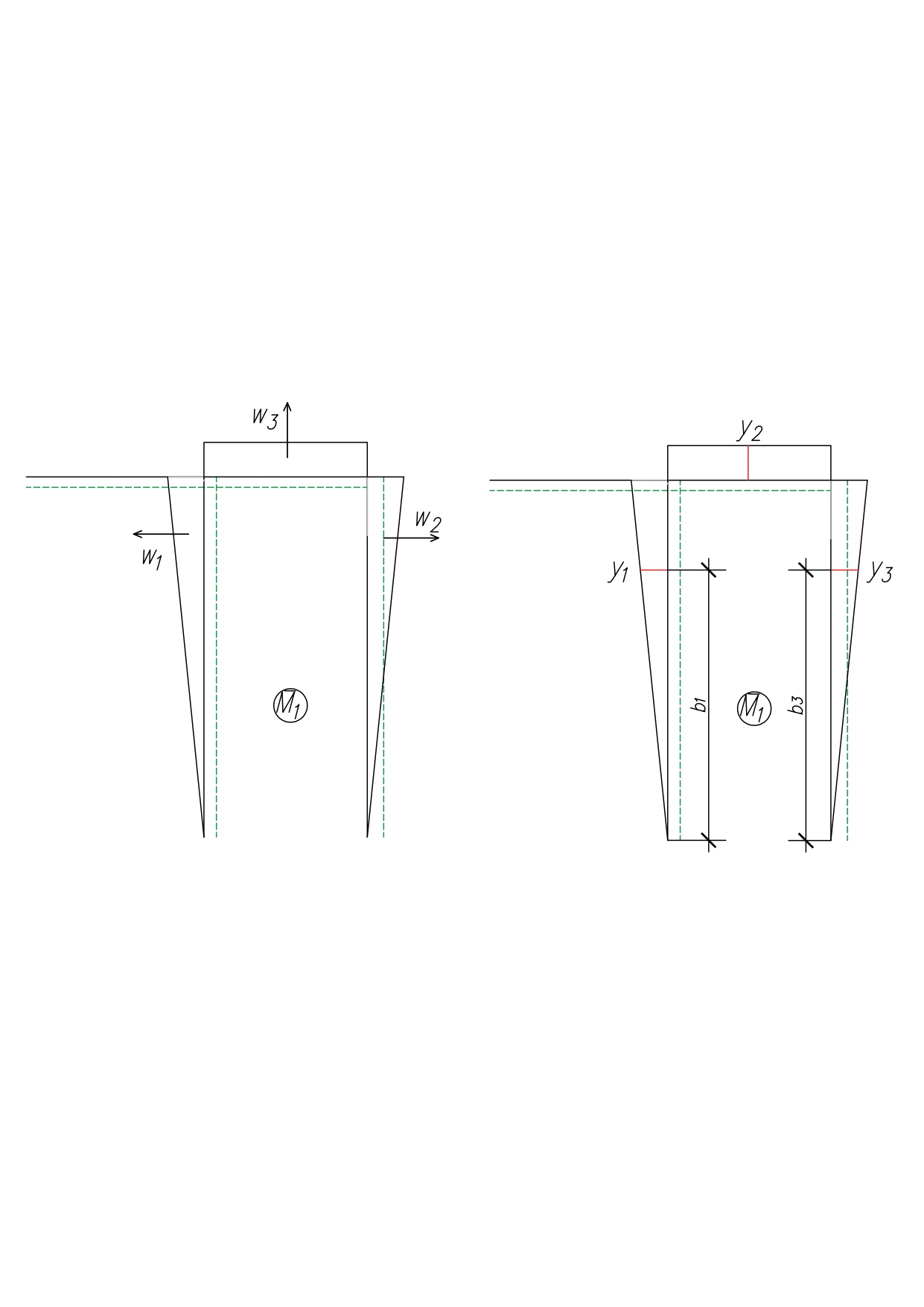
-
а) Определим площади простых фигур грузовой эпюры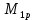
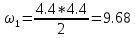 м2 ⊖
м2 ⊖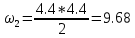 м2 ⊕
м2 ⊕б) Определим ординаты единичной эпюры
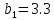 м
м 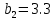 м
м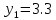 м ⊖
м ⊖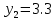 м ⊕
м ⊕ в) Определим перемещение точки 1 от единичной силы
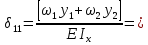
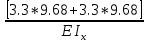 =
= 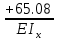 ⊕
⊕-
Определим неизвестную силу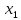 , возникающую в лишней связи
, возникающую в лишней связи
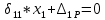
 =
= 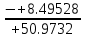 = - 0.17 кН
= - 0.17 кНЗнак «-» показывает, что предположение о направлении действия силы
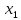 было неверным
было неверным-
Расчет статические определимой рамы
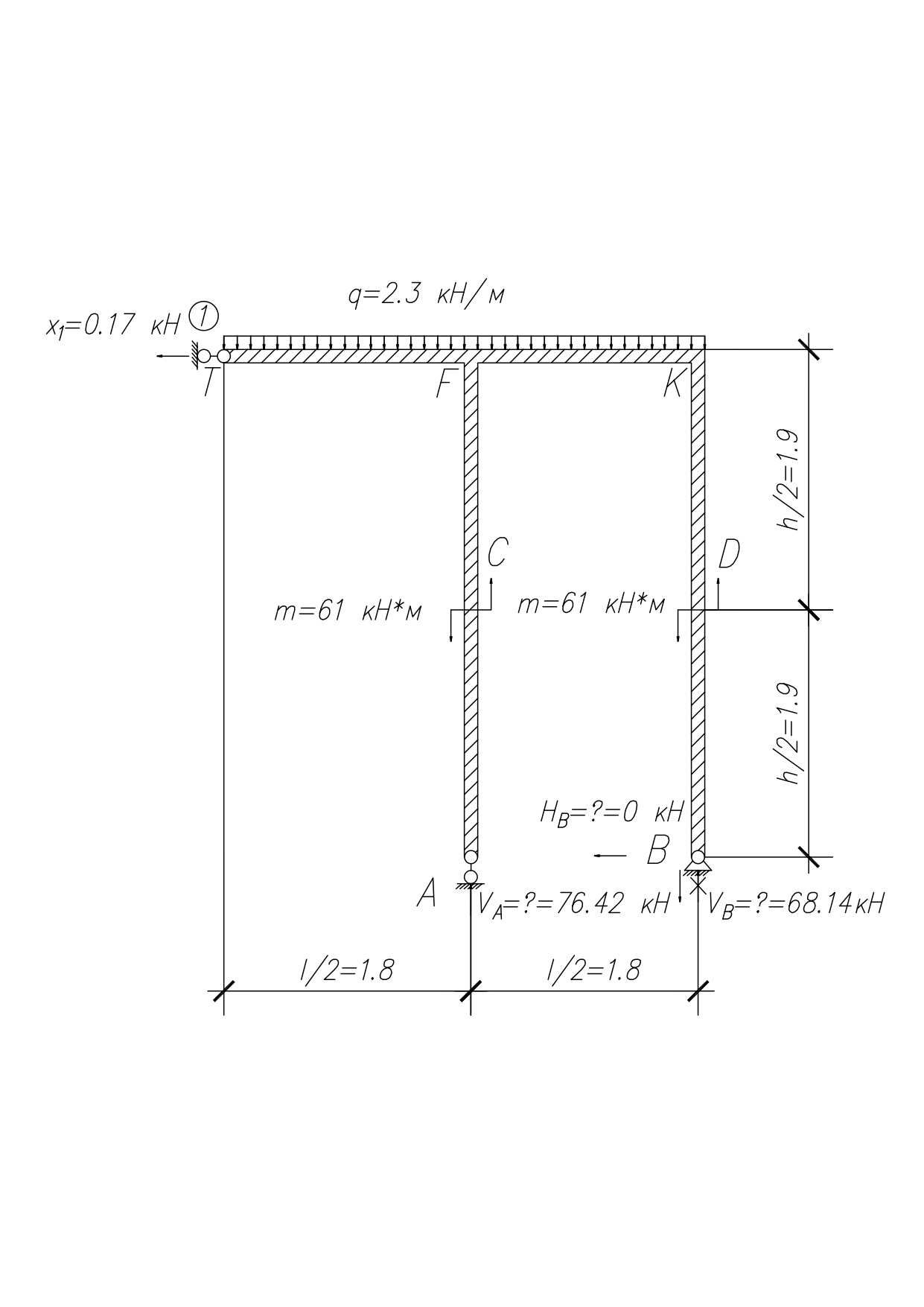 А. Построим эпюры внутренних усилий
А. Построим эпюры внутренних усилий1. Определим опорные реакции
а) Определим опорную реакцию VB
∑mA = 0 → VB +⟲ тм ⟳ –
+ VB * 1.8 + m1 + m2 - [q * 1.8] * 0.9 + [q * 1.8] * 0.9 + x1* 3.8 = 0
+ VB * 1.8 + 61 + 61 - [2.3 * 1.8] * 0.9 + [2.3 * 1.8] * 0.9 + 0.17 * 3.8 = 0
+ VB * 1.8 + 61 + 61 – 3.726 + 3.726 + 0.646 = 0
+ VB * 1.8 = - 122.646
+ VB =
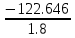
+ VB = - 68.14 кН
VB = 68.14 кН ⊖
б) Определим опорную реакцию VA
∑mB = 0 → VA +⟲ тм ⟳ –
- VA * 1.8 + m1 + m2 + [q * 3.6] * 1.8 + x1* 3.8 = 0
- VA * 1.8 + 61 + 61 + [2.3 * 3.6] * 1.8 + 1.7 * 3.8 = 0
- VA * 1.8 + 61 + 61 + 14.904 + 0.646 = 0
- VA * 1.8 = - 137.55
+ VA =
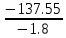
+ VA = + 76.42 кН
VA = 76.42 кН ⊕
в) ∑x = 0 → HB →+ тм ←–
HB – x1 = 0
HB = x1
HB = 0.17 кН ⊕
г) Выполним проверку Ⅰ
∑y = 0 ↑+ тм ↓–
- VB – [q * 3,6] + VA = - 2.3 * 3.6 – 68.14 + 76.42 = 0
д) Выполним проверку ⅠⅠ
∑mM = 0 +⟲ тм ⟳ –
+ VA * 0.9 + m1 + m2 + [q * 0.9] * 0.45 - [q * 2.7] * 1.35 - VB * 2.7 - HB * 3.8 = + 76.42 * 0.9 + 61 + 61 + [2.3 * 0.9] * 0.45 - [2.3 * 2.7] * 1.35 – 68.14 * 2.7 – 0.17 * 3.8 = + 68.778 + 61 + 61 + 0.9315 – 8.3835 – 183.978 – 0.646 = 0
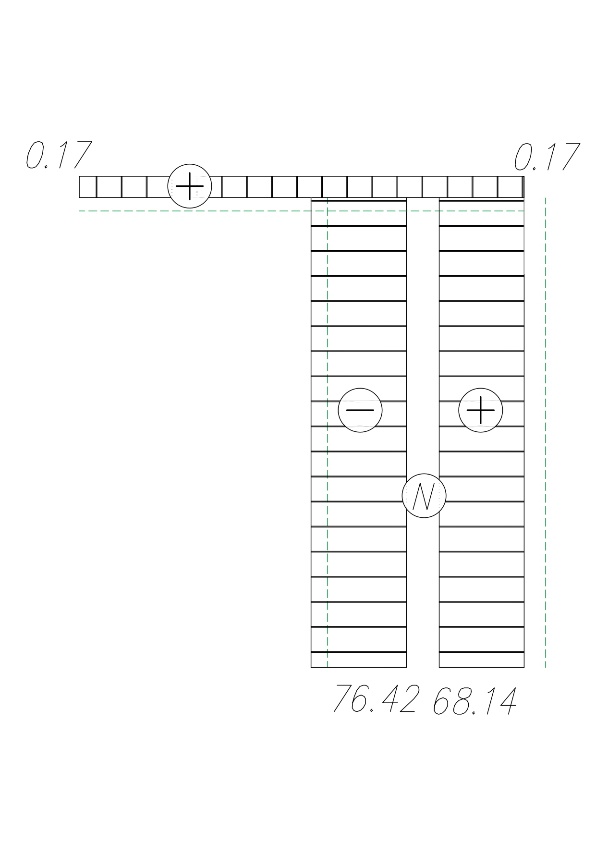
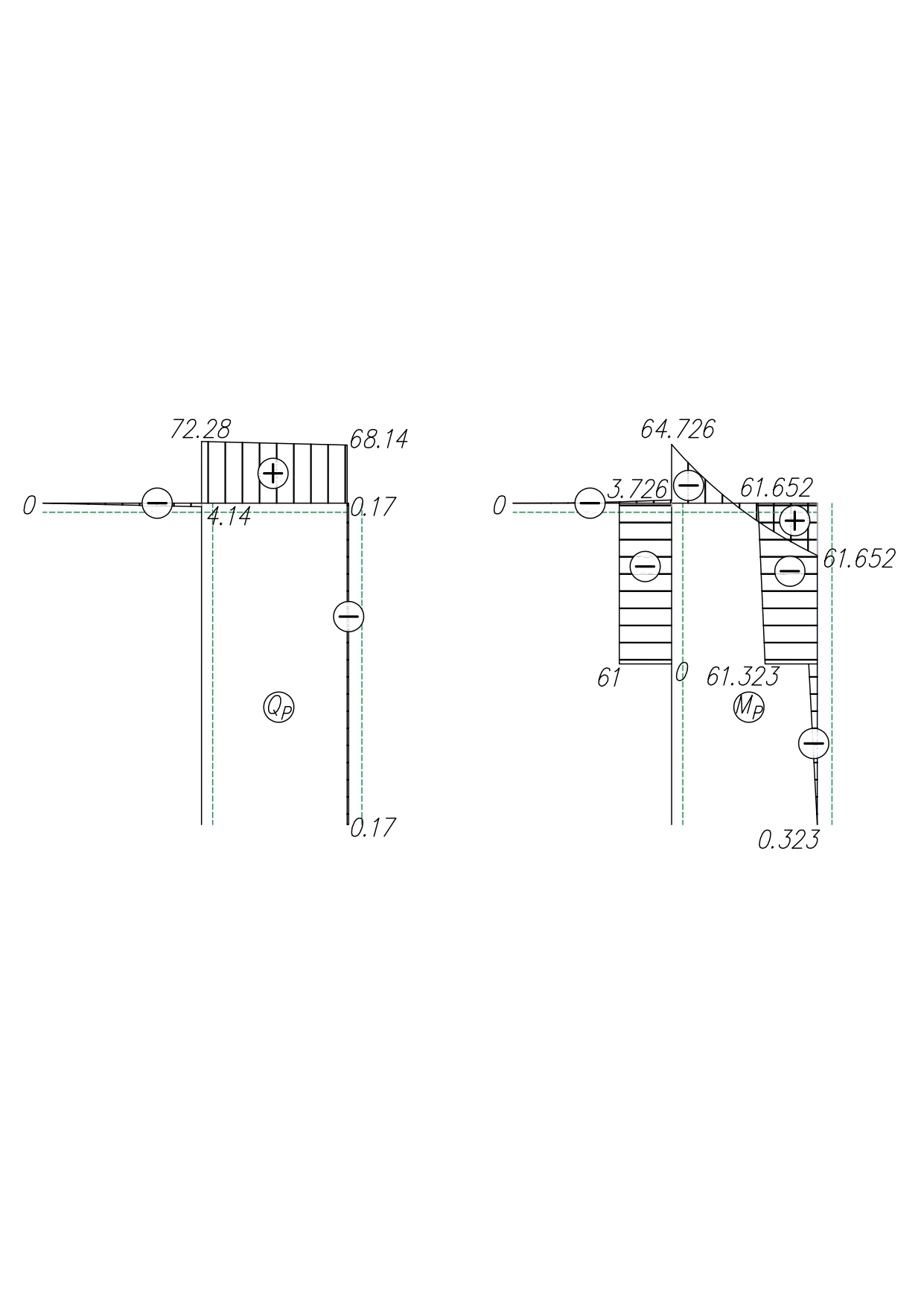 2. Построим эпюры внутренних усилий
2. Построим эпюры внутренних усилий
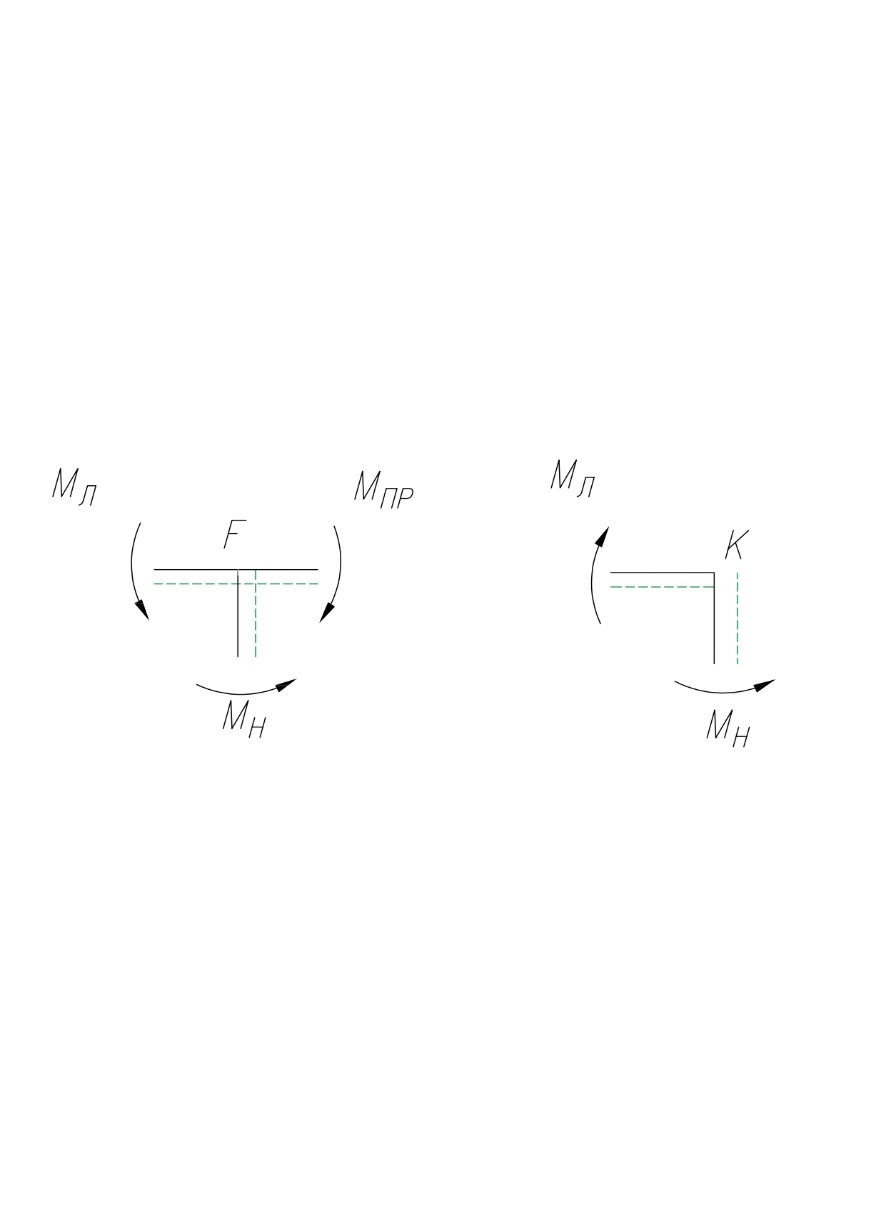
3. Проверим правильность построения эпюры M методом вырезания узлов
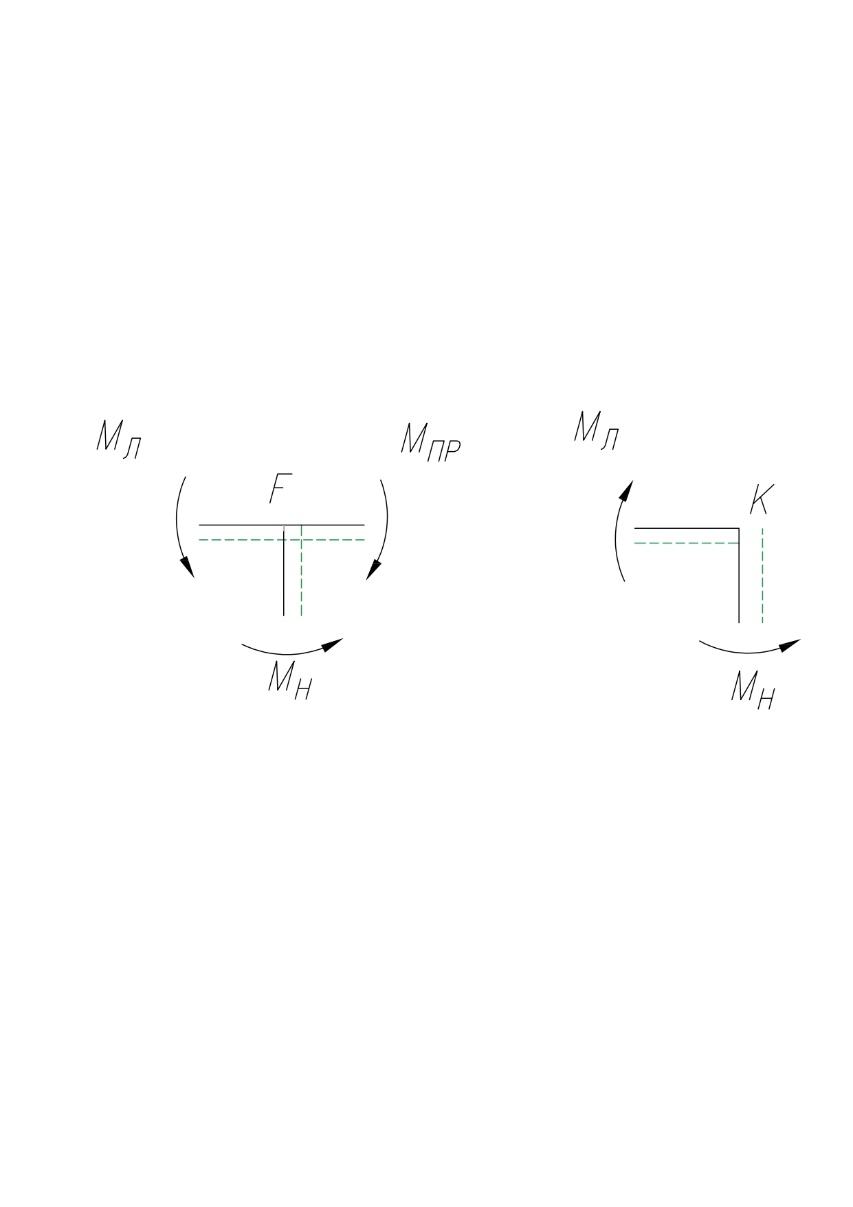
Узел F
∑mF = 0 +⟲ тм ⟳ –
+
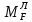 -
- 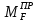 +
+ 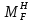 = + 3,726 + 61 – 64,726 = 0
= + 3,726 + 61 – 64,726 = 0Узел K
∑mK = 0 +⟲ тм ⟳ –
-
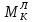 +
+ 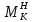 = + 61.652 – 61.652 = 0
= + 61.652 – 61.652 = 0Вывод: узлы F и K находятся в статическом равновесии
4
 . Проверим правильность построения эпюры Q и N методом вырезания узлов
. Проверим правильность построения эпюры Q и N методом вырезания узловУзел F
∑x = 0 →+ тм ←–
- Nпр + Nл = - 0.17 + 0.17 = 0
∑y = 0 ↑+ тм ↓–
- Qпр – Qл + Nл = - 4.14 – 72.28 + 76.42 = 0
Узел K
∑x = 0 →+ тм ←–
-
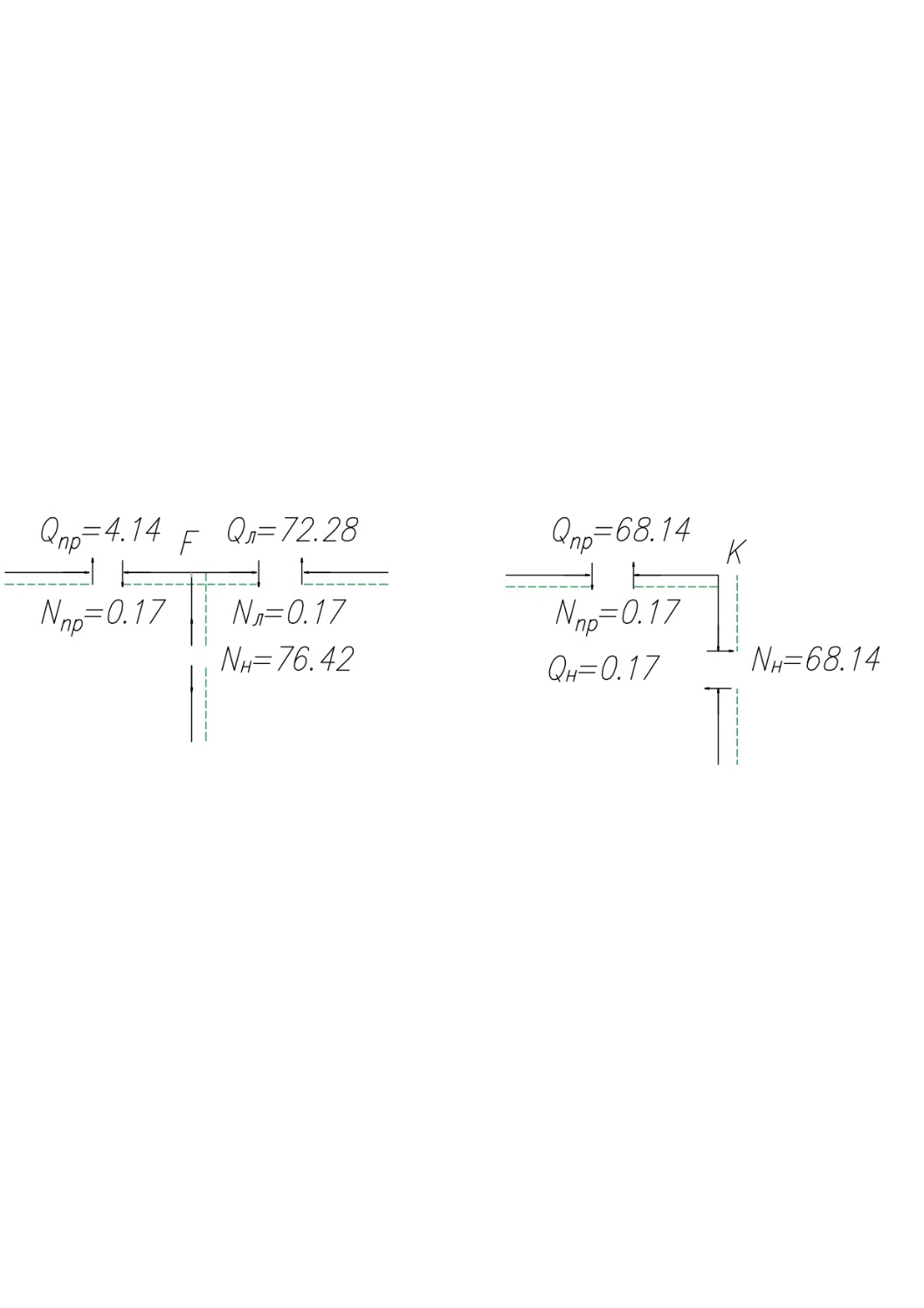 Nпр + Qн = - 0.17 + 0.17 = 0
Nпр + Qн = - 0.17 + 0.17 = 0 ∑y = 0 ↑+ тм ↓–
+ Qпр – Nн = + 68.14 – 68.14 = 0
5. Определим точность нахождения силы x1 при помощи определения перемещения точки 1
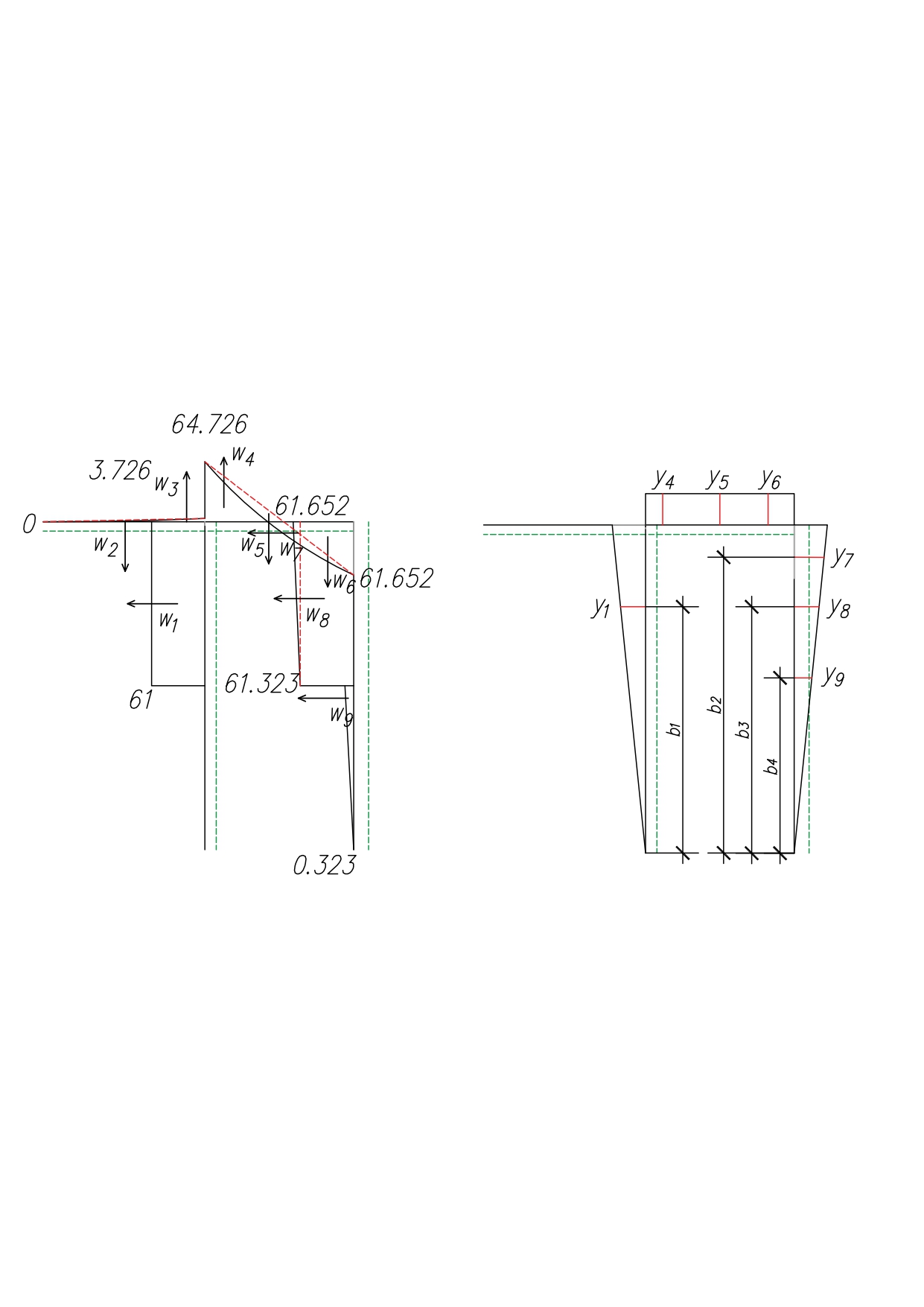
а) Определим площади простых фигур
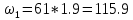 кН*м2 ⊖
кН*м2 ⊖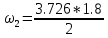 = 3.3534 кН*м2 ⊖
= 3.3534 кН*м2 ⊖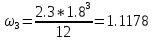 кН*м2 ⊕
кН*м2 ⊕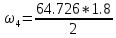 = 58.2534 кН*м2 ⊖
= 58.2534 кН*м2 ⊖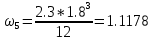 кН*м2 ⊕
кН*м2 ⊕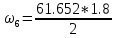 = 55.4868 кН*м2 ⊕
= 55.4868 кН*м2 ⊕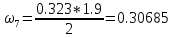 кН*м2 ⊖
кН*м2 ⊖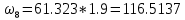 кН*м2 ⊖
кН*м2 ⊖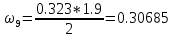 кН*м2 ⊖
кН*м2 ⊖б) Определим ординаты единичной эпюры
