Файл: Решение. Период окупаемости Ток 65000 15000 4,33 года.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.03.2024
Просмотров: 103
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Проект А имеет капитальные вложения в 62000 руб., а ожидаемые чистые денежные поступления составляют 16000 руб. в год в течение 8 лет. Определить период окупаемости этого проекта.
Решение.
Период окупаемости:
Ток = 65000/ 15000= 4,33 года.
-
Инвестор решил вложить свой капитал в приобретение акций металлообрабатывающего предприятия. Цена одной акции составляет 1 тыс. руб. Из проспекта эмиссии следует, что через пять лет стоимость каждой акции утроится.
Определите, выгодна ли сегодня инвестору покупка акций и стоит ли совершать сделку, если существуют другие возможности вложения капитала, обеспечивающие доход на уровне 15% годовых?
Решение:
Для того чтобы сравнить проект (покупку акций) с альтернативным вариантом необходимо найти Чистую приведенную стоимость (ЧПС) проекта по ставке доходности альтернативного варианта. Если ЧПС > 0, значит проект выгодней чем альтернативный вариант и наоборот.
ЧПС = ПС – И,
где И – первоначальные инвестиции (стоимость акции)
И = 1000 руб.
ПС – Приведенная стоимость акции по ставке доходности альтернативного варианта
ПС = С/((1+i)n),
где С – стоимость акции через n лет
С = 1000* 3 = 3000 рублей – стоимость акции через пять лет
ВСД – внутренняя ставка доходности альтернативного проекта
i = 15%
N – количество лет
N = 5 лет
ПС = 3000/((1+15%)5) = 1491,53 руб.
ЧПС = 1491,53 – 1000 = 491,53 руб.
ЧПС >0 , следовательно инвестору выгодней покупать акции, чем вкладывать в другие проекты со ставкой доходности 15%
-
Чтобы заменить морально изношенное технологическое оборудование, проектом предполагается выделить 200 тыс. руб. и затем в течение 10 лет получать ежегодный доход 50 тыс. руб. Определить период окупаемости данного проекта.
Решение. При данных условиях (если отдача по годам распределена равномерно) период окупаемости составит:
Таким образом, ожидается, что сумма первоначальных вложений будет возвращена за 4 года, а в течение следующих 6 лет инвесторы станут получать чистый доход от этих инвестиций.
-
Рассматриваются два проекта. Первый проект предполагает инвестирование 2 млн. рублей за два года и в первый год первый проект может дать прибыль 300 000 рублей. Второй проект предполагает инвестирование 4 млн. рублей за три года и в первый год может дать прибыль 400 000 рублей. Необходимо оценить эффективность указанных проектов, используя показатели рентабельности и срока окупаемости.
Решение. Поскольку информации не хватает (средняя прибыль неизвестна), то при оценке вместо нее используем показатели за первый год эксплуатации.
Рентабельность первого проекта:
Рентабельность второго проекта:
Срок окупаемости первого проекта:
Срок окупаемости второго проекта:
Первый проект выгоднее, так как у него короче срок окупаемости и выше норма прибыли.
5. Предприниматель планирует вложить 7 200 000 руб. в открытие кофейни. Выход на запланированный объем прибыли в 230 000 руб. планируется, начиная с 5-го месяца работы. Годовой показатель прибыли – 2 760 000 руб. Определить срок окупаемости, используя простую формулу расчета.
Решение.
Рассчитаем срок окупаемости, используя простую формулу расчета:
РР = IC / CF = 7 200 000 / 2 760 000 = 2,6 года
Простой срок окупаемости равняется 2,6 года, при этом первые 4 месяца работы не принимают в расчет.
6. Планируется вложить 10000000 руб. в бизнес. Выход на запланированный объем прибыли в 200000 руб. планируется, начиная с 7-го месяца работы. Годовой показатель прибыли – 3 200 000 руб. Определить срок окупаемости (простую формулу расчета).
Решение.
Пример 2 ( наращение по простым ставкам)
Простые процентные ставки применяются к одной и той же сумме долга, в течение всего периода начисления. Сложные применяются по прошествии каждого интервала начисления к основной сумме долга и начисленных на нее за предыдущие интервалы проценты. В мировой практике наибольшее распространение получила схема начисления по сложным ставкам.
Наращенная сумма при использовании простой ставки ссудного процента
где P– первоначальная сумма долга;
i – относительная величина простой ставки ссудного процента;
n – продолжительность периода начисления в годах.
Отсюда
Наращенная сумма при использовании сложной ставки ссудного процента, начисление процентов осуществляется один раз в год
где iс – относительная величина сложной ставки ссудного процента.
Простые процентные ставки применяются к одной и той же сумме долга, в течение всего периода начисления.
Сложные применяются по прошествии каждого интервала начисления к основной сумме долга и начисленных на нее за предыдущие интервалы проценты. В мировой практике наибольшее распространение получила схема начисления по сложным ставкам.
Наращенная сумма при использовании простой ставки ссудного процента
где P– первоначальная сумма долга;
i – относительная величина простой ставки ссудного процента;
n – продолжительность периода начисления в годах.
Отсюда
Наращенная сумма при использовании сложной ставки ссудного процента, начисление процентов осуществляется один раз в год
где iс – относительная величина сложной ставки ссудного процента.
7. Первоначальная сумма Р = 5000 руб. помещена в банк на n = 0,5 года под i = 15% годовых (проценты простые). Найти наращенную сумму.
Решение:
Наращенная сумма поле двух лет S = P (1 + n∙i) = 5000 (1 + 2∙0,15) = 6500 руб.
8. (дисконтирование по простым ставкам)
Наращенная сумма S = 7000 руб., период начисления n = 0,25 года (один квартал), простая процентная ставка i = 12% годовых. Найти первоначальную сумму.
Решение:
Первоначальная сумма Р = S / (1 + n∙i) = 7000 / (1 + 0,25∙0,12) = 6796,12 руб.
9. (наращение по сложным ставкам)
Первоначальная сумма Р = 5000 руб. помещена в банк на n = 2 года под i = 15% годовых (проценты сложные). Найти наращенную сумму.
Решение:
Наращенная сумма после двух лет S = Р (1 + i)n = 5000 (1 + 0,15)2 = 6612,5 руб.
10. (дисконтирование по сложным ставкам)
Наращенная сумма S = 7000 руб., период начисления n = 2 года, сложная процентная ставка i = 12% годовых. Найти первоначальную сумму.
Решение:
Первоначальная сумма Р = S/(1 + i)n = 7000/(1 + 0,12)2 = 5580,36 руб.
11. (нахождение периода начисления)
Первоначальная сумма Р = 3000 руб., наращенная сумма S = 4500 руб., i = 20% годовых (проценты сложные). Найти период начисления.
Решение:
Тогда период начисления n = ln(S/P)/ln(l + i) = ln(4500/3000) / ln(l + 0,2) = 2,2 года.
12.Рассчитать суммарную и среднегодовую прибыль исходя из следующих данных:
- инновационный проект рассчитан на 4 года;
- ожидаемые доходы от реализации проекта составляют 750; 1000; 800; 250 ден.ед.;
- совокупные затраты: 1500; 240; 230; 800 ден. ед.
Суммарная прибыль от реализации проекта:
П = (750 — 1500) + (1000 — 240) + (800 — 230) + (250 - 800) = 30 ден. ед.
Среднегодовая прибыли: 30: 4 = 7,5 ден. ед.
13. Определить NPV проекта, который при первоначальных единовременных инвестициях в 1500 млн. руб. будет генерировать следующий денежный поток доходов: 100, 200, 250, 1300, 1200 млн. руб. Ставка дисконта 10%.
NPV= - 1500 +
Данный проект следует принять.
14. Проект рассчитан на три года, объём инвестиций – 126 млн руб. Чистый денежный поток: 1-й год –– 45 млн руб., 2-й год –– 54 млн руб., 3-й год –– 75 млн руб. Определить NPV, PI.
Решение: NPV проекта определяется как разность между суммой настоящих стоимостей всех денежных потоков доходов и суммой настоящих стоимостей всех денежных потоков затрат, как чистый денежный поток от проекта, приведённый к настоящей стоимости.
NPV = PVдоходов – PVинвестиций = (45+54+75) – 126 = 48 млн руб.
PI инвестиционного проекта показывает величину текущей стоимости в расчёте на каждую денежную единицу чистых инвестиций
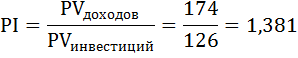 ,
,т.е. 1,381 млн руб. на 1 млн руб. вложенных средств.
15. Инвестор решил вложить свой капитал в приобретение акций металлообрабатывающего предприятия. Цена одной акции составляет 1 тыс. руб. Из проспекта эмиссии следует, что через пять лет стоимость каждой акции утроится.
Определите, выгодна ли сегодня инвестору покупка акций и стоит ли совершать сделку, если существуют другие возможности вложения капитала, обеспечивающие доход на уровне 15% годовых?
Решение:
Для того чтобы сравнить проект (покупку акций) с альтернативным вариантом необходимо найти Чистую приведенную стоимость (ЧПС) проекта по ставке доходности альтернативного варианта. Если ЧПС > 0, значит проект выгодней чем альтернативный вариант и наоборот.
ЧПС = ПС – И,
где И – первоначальные инвестиции (стоимость акции)
И = 1000 руб.
ПС – Приведенная стоимость акции по ставке доходности альтернативного варианта
ПС = С/((1+i)n),
где С – стоимость акции через n лет
С = 1000* 3 = 3000 рублей – стоимость акции через пять лет
ВСД – внутренняя ставка доходности альтернативного проекта
i = 15%
N – количество лет
N = 5 лет
ПС = 3000/((1+15%)5) = 1491,53 руб.
ЧПС = 1491,53 – 1000 = 491,53 руб.
ЧПС >0 , следовательно инвестору выгодней покупать акции, чем вкладывать в другие проекты со ставкой доходности 15%
16. Проект требует вложений в размере 150 000 рублей. Ожидается, что ежегодные поступления от его реализации составят 50 000 рублей. Рассчитать срок окупаемости.
Решение:
Подставим имеющиеся у нас данные в формулу:
РР = 150 000 / 50 000 = 3 года
Таким образом, ожидается, что вложенные средства окупятся в течение трех лет.
17. Проект требует вложений в размере 150 000 рублей. Ожидается, что ежегодные поступления от его реализации составят 50 000 рублей. В процессе реализации проекта существуют ежегодные издержки в размере 20 000 рублей. Рассчитать срок окупаемости.
Решение:
РР = К0 / ПЧсг,
