Файл: Рабочая программа финансовая математика (наименование учебной дисциплины) Уровень основной образовательной программы.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.03.2024
Просмотров: 46
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
учетный или дисконтный множитель.
.
Задача 3.8.Через 5 лет предприятию будет выплачена сумма 1000 000 руб. Определить ее современную стоимость при условии, что применяется ставка сложных процентов –10% годовых.
Р е ш е н и е. По формуле (3.8) находим
Р= 1000 000(1+ 0,10)-5 = 620 921,32 руб.
Если проценты начисляютсяmраз в году, то получим
P = S [1/(1 + j/m)mn] = Svmn (3.9)
где
vmn = 1/(1 + j/m)mn = (1 + j/m)-mn (3.10)
– дисконтный множитель.
Так же, как и в случае начисления простых процентов, величинуР, полученную дисконтированиемS, называютсовременнойилитекущей стоимостьюилиприведенной величинойS.СуммыРиSэквивалентны в том смысле, что платеж в суммеSчерезnлет равноценен суммеР, выплачиваемой в настоящий момент.
Банковский учет.В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле
Р = S (1–dсл)п, (3.11)
где
dсл–сложная годовая учетная ставка.
Дисконт в этом случае равен
D = S – Р = S – S (1– dсл)п = S [1– (1– dсл)п] (3.12)
При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта
.
Задача 3.9.Через 5 лет по векселю должна быть выплачена сумма 1000 000 руб. Банк учел вексель по сложной учетной ставке 10% годовых. Определить дисконт.
Р е ш е н и е. По формуле (3.12) находим
Р= 1 000 000 (1 – 0,10)5 = 590 490,00 руб.;
D = S– Р = 1 000 000 – 590 490 = 409 510 руб.
В случае, когда деньги берутся в долг на срок, меньший 1 года (n < 1), выполняется неравенство
S (1–dсл)п< S (1- пd),
т.е. расчет по схеме сложных процентов более выгоден кредитору.
Если же деньги берутся в долг на срок, больший 1 года (n > 1), выполняется неравенство
S (1–dсл)п> S (1– пd),
т.е. расчет по схеме сложных процентов более выгоден заемщику.
Задача 3.10. Пусть S= 1 000 000,d= 0,12,n = 0,5.
В каком случае плата за кредит больше: при расчете посхеме простых процентов или при расчете посхеме сложных процентов?
Р е ш е н и е. Произведем расчет посхеме простых процентов:
Р = 1 000 000 • (1 – 0,12• 0,5) = 940000.
При расчете посхеме сложных процентов получаем
Р = 1 000 000 • (1 – 0,12) 0,5 = 938083,15.
О т в е т. При расчете посхеме сложных процентов
плата за кредит больше, и заемщик получает «на руки» меньше, чем при расчете посхеме простых процентов.
4.
Непрерывные проценты.
4.1. Наращение и дисконтирование.Наращенная суммав случае непрерывного начисления процентов по ставке j:
S = Pejn. (4.1)
Для того чтобы отличать ставку непрерывных процентов от ставок дискретных процентов, ее называют силой роста и обозначают символомδ.С учетом введенного обозначения равенство (4.1) принимает вид
S = Pe δn(4.2)
Сила роста представляет собой номинальную ставку процентов при m→∞.
Задача 4.1.Сила роста банковского вклада δ=0,03. Найти сумму на счете через 2 года, если первоначальная сумма вклада составляет 9000 руб.
Р е ш е н и е. S= 9000е0,03*2 = 9000е0,06 = 9556,38 руб.
Дисконтирование на основе непрерывных процентных ставок осуществляется по формуле
P = Se-δn(4.3)
4.2. Связь дискретных и непрерывных процентных ставок.
Дискретные и непрерывные процентные ставки находятся в функциональной зависимости, благодаря которой можно осуществлять переход от расчета непрерывных процентов к дискретным и наоборот. Формулу эквивалентного перехода от одних ставок к другим можно получить, приравнивая соответствующие множители наращения
(1 + i)n =eδn(4.4)
Из записанного равенства следует, что
δ = ln (1 + i ), (4.5)
откуда
i
= e δ– 1(4.6)
Задача 4.2.Годовая ставка сложных процентов равна 15%. Чему равна эквивалентная сила роста?
Р е ш е н и е. Воспользуемся формулой (4.5):
δ =ln (1 + i )=ln (1 + 0,15) = 0,13976,
т.е. эквивалентная сила роста равна 13,976%.
Практические задания по теме
«Эквивалентность процентных ставок»
В практике часто возникает необходимость в изменении условий контракта. В связи с тем, что контракты могут быть составлены с использованием различных видов ставок, для сопоставления их доходности возникает необходимость в установлении правил эквивалентного приведения различных ставок к ставке одного вида. Формулы, устанавливающие правила эквивалентного перехода от одной ставки к другой, выводятся на основе принципа финансовой эквивалентности результатов наращения (или дисконтирования) по этим ставкам.
Задача 5.1. Кредит на 2 года получен под 60% номинальную ставку сложных процентов. Начисление происходит ежеквартально. Оценить эффективность операции через эквивалентные простую и сложные ставки процентов.
Р е ш е н и е. j=0,6; n=2; m=4.
a)Эквивалентная ставка простых процентов:
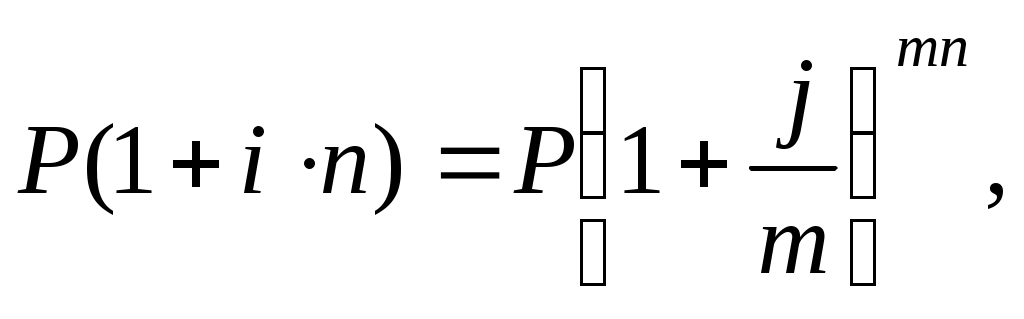
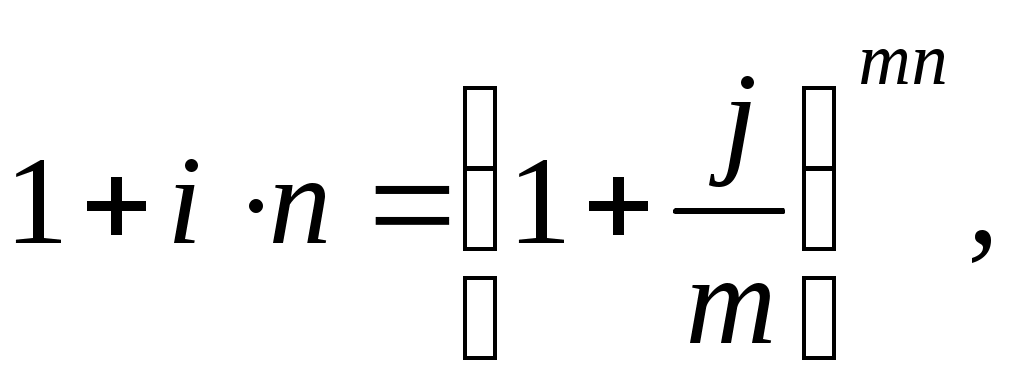
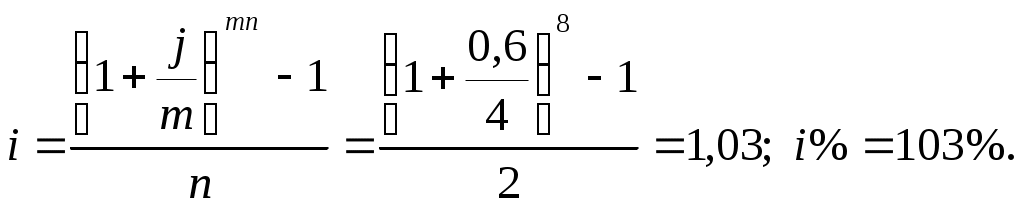
б) Эквивалентная эффективная ставка сложных процентов:
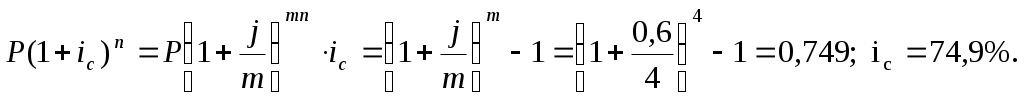
Задача 5.2. Определить, под какую простую ставку процентов выгоднее поместить капитал на 1 год: с ежемесячным начислением 10%, с ежеквартальным начислением 100% или с ежегодным 1000%.
Р е ш е н и е:Доходность вариантов сравниваем по величине годовых ставок простых процентов:
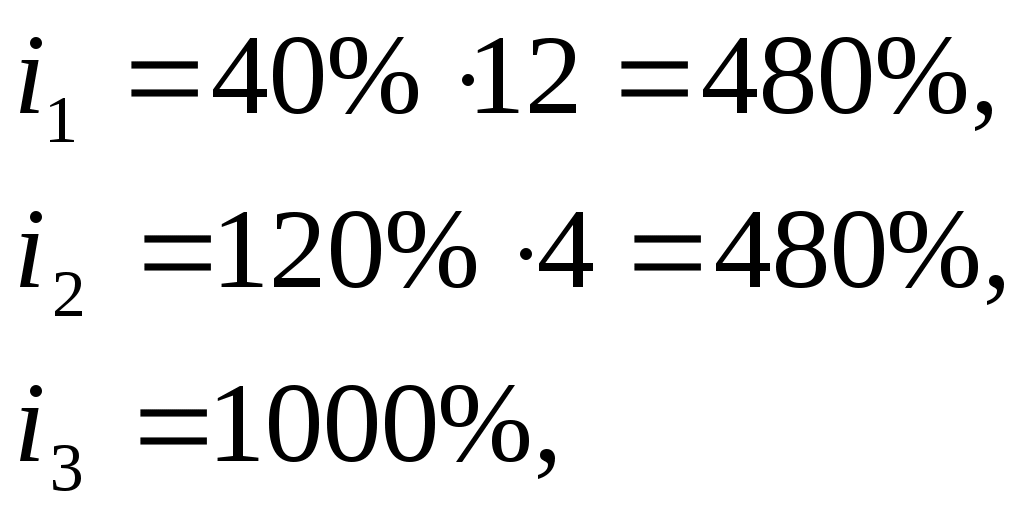
очевидно i3>i1=i2.
Следует заметить, что приведенные данные были в реальной ситуации на фондовом рынке и, как правило, по третьему варианту вкладчики так ничего и не получили (даже своего вклада), а вот по первому варианту, используя реинвестирование по трехмесячным контрактам получили финансовый результат превышающий третий вариант.
Практические задания по теме
.
Задача 3.8.Через 5 лет предприятию будет выплачена сумма 1000 000 руб. Определить ее современную стоимость при условии, что применяется ставка сложных процентов –10% годовых.
Р е ш е н и е. По формуле (3.8) находим
Р= 1000 000(1+ 0,10)-5 = 620 921,32 руб.
Если проценты начисляютсяmраз в году, то получим
P = S [1/(1 + j/m)mn] = Svmn (3.9)
где
vmn = 1/(1 + j/m)mn = (1 + j/m)-mn (3.10)
– дисконтный множитель.
Так же, как и в случае начисления простых процентов, величинуР, полученную дисконтированиемS, называютсовременнойилитекущей стоимостьюилиприведенной величинойS.СуммыРиSэквивалентны в том смысле, что платеж в суммеSчерезnлет равноценен суммеР, выплачиваемой в настоящий момент.
Банковский учет.В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле
Р = S (1–dсл)п, (3.11)
где
dсл–сложная годовая учетная ставка.
Дисконт в этом случае равен
D = S – Р = S – S (1– dсл)п = S [1– (1– dсл)п] (3.12)
При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта
.
Задача 3.9.Через 5 лет по векселю должна быть выплачена сумма 1000 000 руб. Банк учел вексель по сложной учетной ставке 10% годовых. Определить дисконт.
Р е ш е н и е. По формуле (3.12) находим
Р= 1 000 000 (1 – 0,10)5 = 590 490,00 руб.;
D = S– Р = 1 000 000 – 590 490 = 409 510 руб.
В случае, когда деньги берутся в долг на срок, меньший 1 года (n < 1), выполняется неравенство
S (1–dсл)п< S (1- пd),
т.е. расчет по схеме сложных процентов более выгоден кредитору.
Если же деньги берутся в долг на срок, больший 1 года (n > 1), выполняется неравенство
S (1–dсл)п> S (1– пd),
т.е. расчет по схеме сложных процентов более выгоден заемщику.
Задача 3.10. Пусть S= 1 000 000,d= 0,12,n = 0,5.
В каком случае плата за кредит больше: при расчете посхеме простых процентов или при расчете посхеме сложных процентов?
Р е ш е н и е. Произведем расчет посхеме простых процентов:
Р = 1 000 000 • (1 – 0,12• 0,5) = 940000.
При расчете посхеме сложных процентов получаем
Р = 1 000 000 • (1 – 0,12) 0,5 = 938083,15.
О т в е т. При расчете посхеме сложных процентов
плата за кредит больше, и заемщик получает «на руки» меньше, чем при расчете посхеме простых процентов.
4.
Непрерывные проценты.
4.1. Наращение и дисконтирование.Наращенная суммав случае непрерывного начисления процентов по ставке j:
S = Pejn. (4.1)
Для того чтобы отличать ставку непрерывных процентов от ставок дискретных процентов, ее называют силой роста и обозначают символомδ.С учетом введенного обозначения равенство (4.1) принимает вид
S = Pe δn(4.2)
Сила роста представляет собой номинальную ставку процентов при m→∞.
Задача 4.1.Сила роста банковского вклада δ=0,03. Найти сумму на счете через 2 года, если первоначальная сумма вклада составляет 9000 руб.
Р е ш е н и е. S= 9000е0,03*2 = 9000е0,06 = 9556,38 руб.
Дисконтирование на основе непрерывных процентных ставок осуществляется по формуле
P = Se-δn(4.3)
4.2. Связь дискретных и непрерывных процентных ставок.
Дискретные и непрерывные процентные ставки находятся в функциональной зависимости, благодаря которой можно осуществлять переход от расчета непрерывных процентов к дискретным и наоборот. Формулу эквивалентного перехода от одних ставок к другим можно получить, приравнивая соответствующие множители наращения
(1 + i)n =eδn(4.4)
Из записанного равенства следует, что
δ = ln (1 + i ), (4.5)
откуда
i
= e δ– 1(4.6)
Задача 4.2.Годовая ставка сложных процентов равна 15%. Чему равна эквивалентная сила роста?
Р е ш е н и е. Воспользуемся формулой (4.5):
δ =ln (1 + i )=ln (1 + 0,15) = 0,13976,
т.е. эквивалентная сила роста равна 13,976%.
Практические задания по теме
«Эквивалентность процентных ставок»
В практике часто возникает необходимость в изменении условий контракта. В связи с тем, что контракты могут быть составлены с использованием различных видов ставок, для сопоставления их доходности возникает необходимость в установлении правил эквивалентного приведения различных ставок к ставке одного вида. Формулы, устанавливающие правила эквивалентного перехода от одной ставки к другой, выводятся на основе принципа финансовой эквивалентности результатов наращения (или дисконтирования) по этим ставкам.
Задача 5.1. Кредит на 2 года получен под 60% номинальную ставку сложных процентов. Начисление происходит ежеквартально. Оценить эффективность операции через эквивалентные простую и сложные ставки процентов.
Р е ш е н и е. j=0,6; n=2; m=4.
a)Эквивалентная ставка простых процентов:
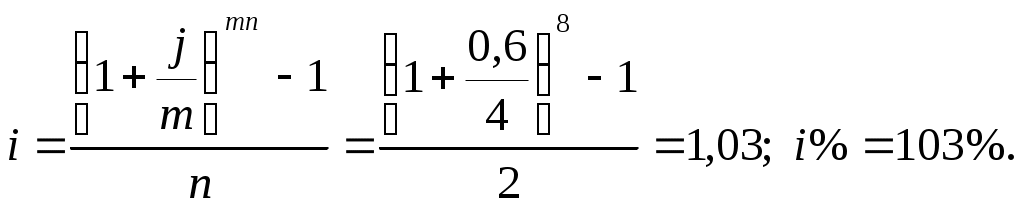
б) Эквивалентная эффективная ставка сложных процентов:
Задача 5.2. Определить, под какую простую ставку процентов выгоднее поместить капитал на 1 год: с ежемесячным начислением 10%, с ежеквартальным начислением 100% или с ежегодным 1000%.
Р е ш е н и е:Доходность вариантов сравниваем по величине годовых ставок простых процентов:
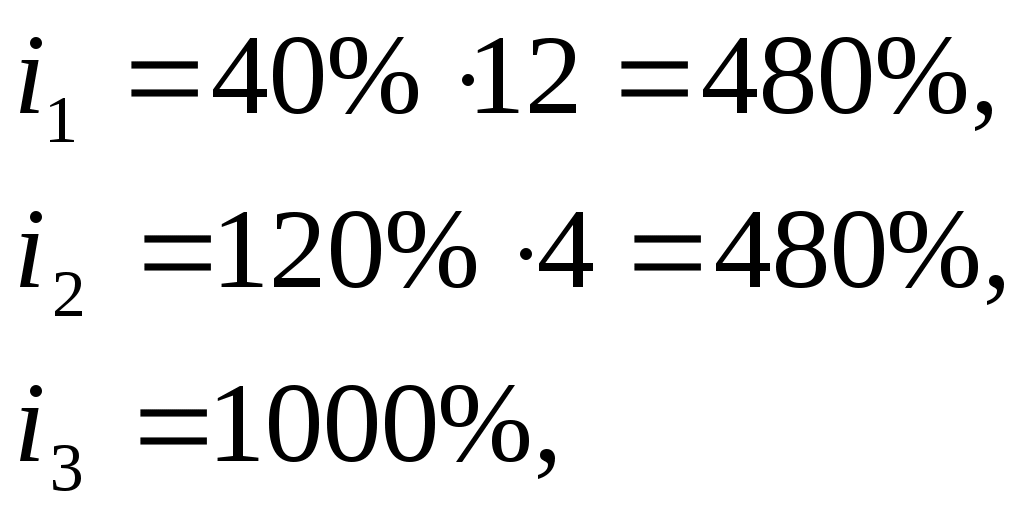
очевидно i3>i1=i2.
Следует заметить, что приведенные данные были в реальной ситуации на фондовом рынке и, как правило, по третьему варианту вкладчики так ничего и не получили (даже своего вклада), а вот по первому варианту, используя реинвестирование по трехмесячным контрактам получили финансовый результат превышающий третий вариант.
Практические задания по теме


