У нас, а=x-3, b=2

Х-3=3, x=3+3, x=6

Сделаем проверку, для этого подставим в исходное уравнение.



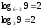
2=2-верно.

Ответ: 6.



Воспользуемся формулой:



Тогда:



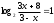
Если, , значит под логарифмическое выражение из уравнения будет равно 2: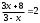



Перенесём всё в левую часть уравнения:



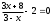
Приведём к одному знаменателю:



Решим уравнение, как систему уравнений. Так как дробь равна нулю, когда знаменатель не равен нулю, а числитель равен нулю:



Сделаем проверку, для этого подставим в исходное уравнение:



Воспользуемся формулой:





1=1-верно

Ответ: .

Задание 5. 

Решите предложенные неравенства, подробно описывая ход решения (указывайте формулы и положения, которыми пользуетесь, записывайте промежуточные результаты):



Решение:

 

Это показательное уравнение имеет вид:

Запишем неравенство в таком виде:

Логарифмирование:

Теперь возьмём от обоих частей неравенства логарифм по основанию 3. Мы имеем право это делать, так как обе части неравенства больше нуля. Основание логарифма больше единицы, поэтому знак неравенства не изменится.

---

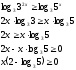
Разделим на (2- ), предварительно исследовав знак этого выражения, так как 2- >0, <2

Получим:



Ответ:



Пусть log₂x=t



Разложим (-5t) как (-3t-2t):



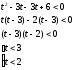
Делаем обратную замену:



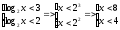
Ответ: х<4 или ∞)

Задание 6.

Решите предложенные тригонометрические уравнения и неравенства, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, отобразите графически на единичной окружности соответствующие точки и интервалы):

 

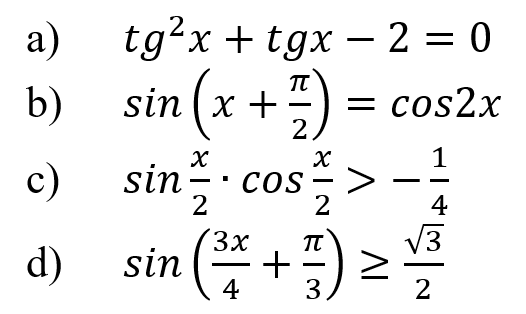
Решение:



Сделаем замену тригонометрической функции tg(x)=у:



Получаем квадратное уравнение. Решим его, используя дискриминант (a=1,b=1,c=-2)



Делаем обратную подстановку:

1. 
   tgx=2 => x₁=arctg(-2)+ k
   
2. 
   tgx=-1=>x₂= + k
   

π



Разложим вторую часть уравнения, согласно тригонометрическому тождеству и формуле двойного угла:

---

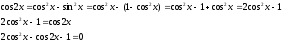
Сделаем замену cosx=t



Делаем обратную замену:

1. 
   cosx=
   
2. 
   
   

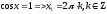
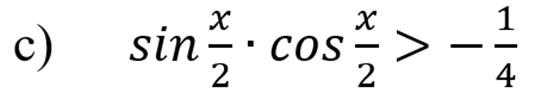
Умножим обе части неравенства на 2:



Используем формулу половинного аргумента:









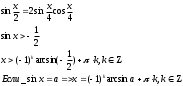
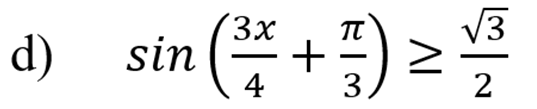
Чтобы решить это неравенство – надо сначала решить соответствующее уравнение:

-это простейшее тригонометрическое уравнение, которое преобразуется в:



Перенесём в правую часть уравнения с противоположным знаком:



Разделим обе части уравнения на :



Данные точки являются точками смены знака неравенства в решениях.





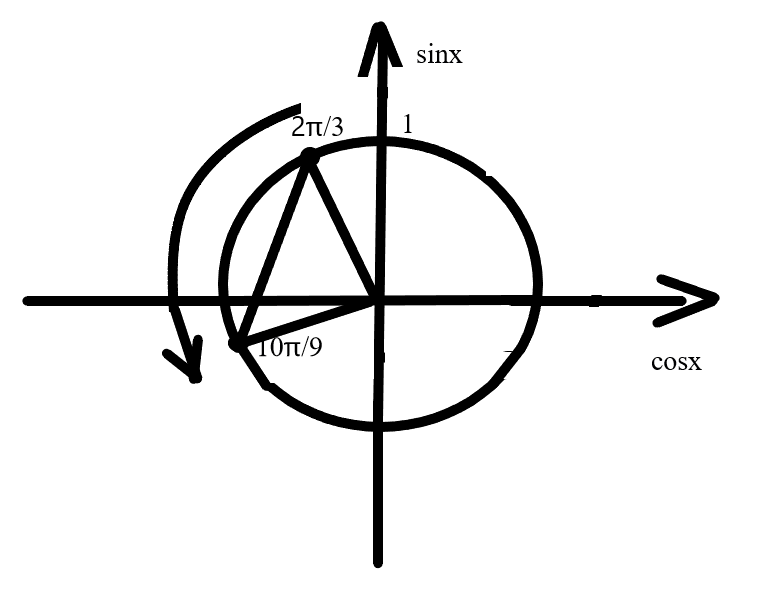
Задание 7.

Вычислите предложные производные функций, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты):



Решение:



Представим производную в виде суммы производных:

---

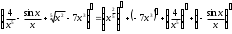
Производную этого выражения находим по формуле: (xⁿ)' = n*x^n-1



x^′=1

(-7·x³) ^′=-7·3·x^3-1·x^′=-21·x²

x^′=1





При вычислении были использованы следующие правила дифференцирования: (x^a)' = ax^a-1
(a)' = 0,



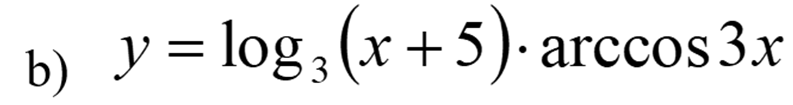
Используем формулу:

Найдем производную первого члена, используя формулу из таблицы производных:



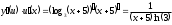
Производная от логарифма и под логарифмического выражения:



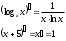
Найдем производную второго члена, используя формулы из таблицы производных и свойство сложной функции:



Производная от тригонометрической функции и производная с константой:



Результат:

Задание 8.

 Вам предложена функция: 

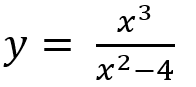
Проведите исследование, согласно схеме:

1.    Найти область определения функции.

2.    Найти точки пересечения с осями.

3.    Исследовать функцию на четность/нечетность.

4.    Найти асимптоты.

5.    Найти экстремумы и интервалы монотонности функции.

6.    Найти интервалы выпуклости функции и точки перегиба.

7.    Найти дополнительные точки, уточняющие график.

8.    Построить график.

 Решение:

1. 
   Найти область определения функции.
   

Точки разрыва:



Значит, область определения функции:

∞;-4)

---

(-4;4) (4;+∞)

2. 
   Найти точки пересечения с осями. Приравняем к нулю.
   

Пересечение с осью 0Y: x=0, y=0

Пересечение с осью 0X:

y=0, тогда 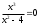, х=0

3. 
   Исследовать функцию на четность/нечетность:
   

y(-x) = -y(x), нечетная функция

4. 
   Найти асимптоты:
   

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:



Находим коэффициент k:





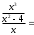
Находим коэффициент b:





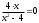
Получаем уравнение наклонной асимптоты:

y = x
Найдем вертикальные асимптоты. Для этого определим точки разрыва:

x₁ = -2, x₂ = 2
Находим переделы в точке x=-2





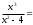
x₁ = -2 - точка разрыва II рода и является вертикальной асимптотой.
Находим переделы в точке x=2

---

Смотрите также файлы

• Обучающийся Чирясова Оксана Федоровна Преподаватель Чащинова Анна Вадимовна Экологические основы природопользования (ДО, пнк, пдо, 2 часть) Практическое занятие.rtf

• Характеристика исламской финансовой системы.docx

• 2 Верно Баллов 1,00 из 1,00 Отметить вопрос Текст вопроса Вид познания, вплетенный в ткань жизнедеятельности субъекта, но не обладающий доказательной силой,.docx

• 2 4 дыбысты файлдарды деу.doc

• Закон Об электронной цифровой подписи.docx