Выполните задания с учетом исходных данных, подробно описывая ход вашего решения:

• 
  Построить полигон распределения.
  
• 
  Вычислить выборочную среднюю, дисперсию, моду, медиану.
  
• 
  Построить выборочную функцию распределения.
  

Построим дискретный вариационный ряд. Для этого подсчитаем количество повторения для каждого элемента ряда.

Xi	1	2	4	5
ni	2	2	3	3

Таблица для расчета показателей.

Xi	Кол-во, fi	Xi·fi	Накопленная частота, S	|x-xср|·fi	(x-xср)2·fi	Относительная частота, fi/f
1	2	2	2	4.6	10.58	0.2
2	2	4	4	2.6	3.38	0.2
4	3	12	7	2.1	1.47	0.3
5	3	15	10	5.1	8.67	0.3
Итого	10	33		14.4	24.1	1

Построим полигон распределения, для этого на оси абсцисс отметим значения случайной величины, а на оси ординат – частоты значений случайной величины (кол-во повторений в ряду) и соединим точки линиями, получим:



Рассчитаем выборочную среднюю (среднюю взвешенную):



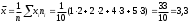
Дисперсия случайной величины найдём по формуле, значения возьмём из расчётной таблицы:



Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.

---

Имеются два показателя с одинаковым значением частоты f=3. Ряд имеет две моды, т.е. является бимодальным.

Медиана.

Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим xi, при котором накопленная частота S будет больше ∑f/2 = 6. Это значение xi = 4. Таким образом, медиана равна 4.

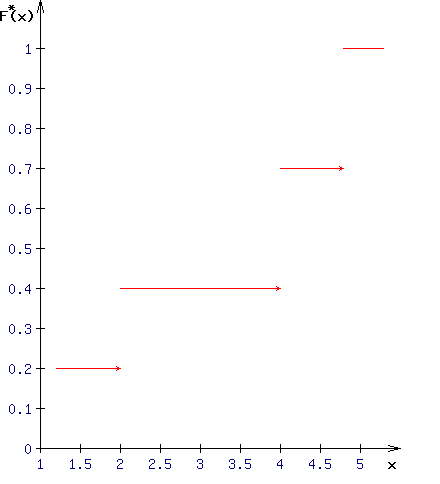
Построим выборочную (эмпирическую) функцию распределения. Для этого возьмём данные из колонки «Относительная частота» расчётной таблицы и подсчитаем значения F(x):

F(x) = 0, при x<1

F(x) = 0.2, при 1 2

F(x) = 0.2+0.2=0.4, при 2 4

F(x) = 0.4+03=0.7, при 4 5

F(x) = 0.7+0.3=1, при x>5




4>

---

Смотрите также файлы

• Обучающийся Чирясова Оксана Федоровна Преподаватель Чащинова Анна Вадимовна Экологические основы природопользования (ДО, пнк, пдо, 2 часть) Практическое занятие.rtf

• Характеристика исламской финансовой системы.docx

• 2 Верно Баллов 1,00 из 1,00 Отметить вопрос Текст вопроса Вид познания, вплетенный в ткань жизнедеятельности субъекта, но не обладающий доказательной силой,.docx

• 2 4 дыбысты файлдарды деу.doc

• Закон Об электронной цифровой подписи.docx