Файл: Программа среднего профессионального образования 44. 02. 03 Педагогика дополнительного образования (в области социальнопедагогической деятельности) Дисциплина Математика. Практическое занятие 6.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 23
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


x2 = 2 - точка разрыва II рода и является вертикальной асимптотой.
Найдем наклонную асимптоту при x → -∞:
Находим коэффициент k:


Находим коэффициент b:


Получаем уравнение наклонной асимптоты:
y = x
-
Найти y = x^3/(x^2-4)
Найдем точки разрыва функции: x1 = 2, x2 = -2
Поскольку f(-x)=-f(x), то функция является нечетной. экстремумы и интервалы монотонности функции:
-
Находим интервалы возрастания и убывания. Первая производная.
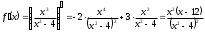
Находим нули функции. Для этого приравниваем производную к нулю
x2·(x2-12) = 0
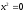 или
или 
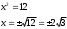
x1 = 0,
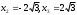
| (-∞;-2  ) ) | (-2  ;-2) ;-2) | (-2;0) | (0;2) | (2;2  ) ) | (2  ;+∞) ;+∞) |
| f'(x)> 0 | f'(x) <0 | f'(x) <0 | f'(x) <0 | f'(x) <0 | f'(x)> 0 |
| функция возрастает | функция убывает | функция убывает | функция убывает | функция убывает | функция возрастает |
В окрестности точки x = -2
 производная функции меняет знак с (+) на (-). Следовательно, точка x = -2
производная функции меняет знак с (+) на (-). Следовательно, точка x = -2 - точка максимума. В окрестности точки x = 2
- точка максимума. В окрестности точки x = 2 производная функции меняет знак с (-) на (+). Следовательно, точка x = 2
производная функции меняет знак с (-) на (+). Следовательно, точка x = 2 - точка минимума.
- точка минимума.-
Найдем интервалы выпуклости и вогнутости функции. Вторая производная.

Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
 => точки перегиба: x1 = 0
=> точки перегиба: x1 = 0| (-∞ ;-2) | (-2; 0) | (0; 2) | (2; +∞) |
| f''(x) <0 | f''(x)> 0 | f''(x) <0 | f''(x)> 0 |
| функция выпукла | функция вогнута | функция выпукла | функция вогнута |
-
Найти дополнительные точки, уточняющие график:
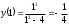
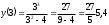


-
Построить график.
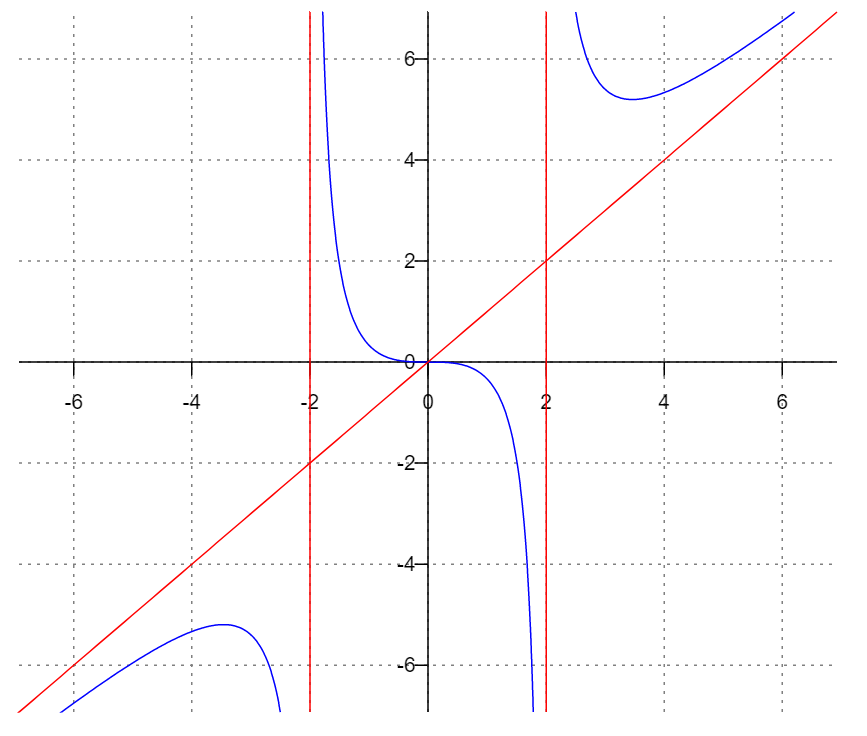
Задание 9.
Вычислите предложенные неопределенные интегралы, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты).

Решение:
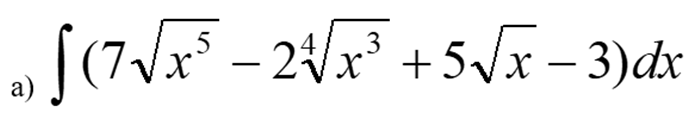
Представим исходный интеграл, как сумму интегралов:

Поочередно решим каждый интеграл, используя свойства интегралов:

Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции. Также представим подкоренное выражение в виде значении со степенью:
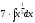
Интеграл от хn есть
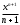 , когда n
, когда n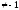 . Применим формулу:
. Применим формулу: 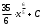

Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции. Также представим подкоренное выражение в виде значении со степенью:

Интеграл от хn есть
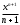 , когда n
, когда n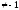 . Применим формулу:
. Применим формулу: 
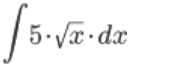
Интеграл от хn есть
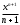 , когда n
, когда n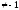 . Применим формулу:
. Применим формулу: 
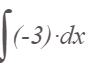
Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции.



Выражение -sin(x) подведем под знак дифференциала, т.е.:
(-sin(x))·dx=d (cos(x)); t=cos(x)
Тогда исходный интеграл можно записать так:

Делаем замену переменных: u=t+2
Тогда, по таблице простейших интегралов:


Возвращаемся к t:
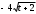
Чтобы записать окончательный ответ, осталось вместо t подставить cos(x):

Задание 10.
Вычислите площадь предложенной криволинейной трапеции, ограниченной графиками функций f(x) и g(x), подробно описывая ход решения (указывайте формулы, которыми пользуетесь, отобразите графики функций и получившуюся фигуру, записывайте промежуточные результаты):

Решение:
График функции f(x)=x–1 – прямая. строим по двум точкам (0;–1) и (1;0)
График функции g(x)=x2–4x+3 – парабола, ветви вверх, вершина в точке (2; –1)
Найдем абсциссы точек пересечения графиков. Для этого приравняем значения с «х» друг к другу.
x–1=x2–4x+3
x2–5x+4=0. Получается квадратное уравнение. Находим дискриминант:
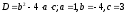
D=(5)2-4*1*3=25–16=9
Находим корни уравнения по формуле, используя дискриминант:

x1=1; x2=4
Применяем формулу:
 , a=x1; b=x2
, a=x1; b=x2S=
 ((x−1)−(x2
((x−1)−(x2
−4x+3))dx=
 (x−1−x2+4x−3)dx=
(x−1−x2+4x−3)dx=  (5x−4−x2)dx=(5*
(5x−4−x2)dx=(5* −4x−
−4x− )
)  =
==(5
 −4⋅4−
−4⋅4−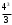 )−(5
)−(5 −4⋅1−
−4⋅1−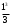 )=
)=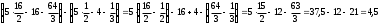

Задание 11.
Решите предложенную задачу, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, отобразите графически полученное решение):
Найдите объем многогранника, вершинами которого являются точки A, A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 6 см2, а боковое ребро равно 4 см.
Решение:
В основаниях призмы Δ АВС и Δ A1B1C1
По условию Sосн=SΔ АВС =SΔ A1B1C1
A A1=ВВ1=СС1=Hпризмы=4
В основании пирамиды A A1B1C1
Δ A1B1C1
Hпирамиды=Hпризмы=4
Vпирамиды A A1B1C1=(1/3)Sосн·H=(1/3)·6·4=8
 Задание 12.
Задание 12. Изучите предложенные исходные данные, полученные при измерении:
| Номер измерения | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Данные | 1 | 1 | 2 | 2 | 4 | 4 | 4 | 5 | 5 | 5 |

