Файл: Курс лекций по дисциплине Цифровая схемотехника для специальности.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 100
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Примеры
Пример 2.1.1.
Найти сумму чисел 10102и 10101 2
Решение.
01010
+ 10101
11111
Учитывая, что 10102= 1010и 101012 = 2110получаем 10 + 21 =31
Действительно, согласно формуле
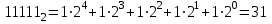
Пример 2.1.2.
Найти разность чисел 101012и 10102
10101
-01010
01011
Пример 2.1.3. Найти произведение чисел 101112 и 112
Решение.
10111
* 11
+10111
10111
1000101
Пример 2.1.4. Найти частное чисел 1101011102и 10102.
Решение.
В частном смело пишем первую 1, т.к. число в двоичной системе не может начинаться с 0. Умножаем эту 1 на делитель, результат правильно записываем под делимом, соблюдая разрядность. Выполняем вычитание по правилам вычитания в двоичной системе счисления. Сносим следующую цифру делимого, и полученное число сравниваем с делителем. В данном случае – полученное число меньше делителя, в частном записываем 0 (в противном случае – 1). Сносим следующую цифру делимого. Получили число равное делителю, в частном записываем 1, и т.д
110101110|1010
-1010 101011
1101
-
1010
1111
-
1010
1010
-
1010
0
Пример 2.1.5. Провести сложение в восьмеричной системе счисления
числа 5 с числами 1, 2, 3, 4.
Решение. 5+1 = 6,
5 + 2=7,
5 + 3 = 10,
5 + 4 = 11
Пример 2.1.6. Выписать таблицу умножения для числа 6 с числами от 1 до 11 в восьмеричной системе счисления.
Решение.
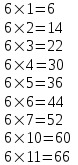
Пример 2.1.7. Найти сумму в восьмеричной системе счисления чисел 365,5 и 74,3.
Решение.
365,5
+ 47,3
462,0
Пример 2.1.8. Найти сумму в шестнадцатеричной системе счисления чисел А6Е,9 и FD,8
Решение.
А6Е,9
+ FD,8
B6C,1
Пример 2.1.9.
Найти разность в восьмеричной системе счисления от чисел 140 и 32.
Решение.
108810 8-2=6
14 0
- 3 2
10 6
Пример 2.1.10. Найти разность в восьмеричной системе счисления чисел 365,5 и 74,3.
Решение.
16-7
365,5
- 74,3
271,2
Пример 2.1.11.
Найти разность в шестнадцатеричной системе счисления чисел A6E,9 иFD,8.
Решение.
16-F=7
A6E,9
- FD,8
971,1
Пример 2.1.12. Заданы числа А16= FA, B16 = 75. Найти А + В и А-В.
Решение.
FA FA
+ 75 - 75
16F 85
Пример 2.1.13. Найти произведение в троичной системе счисления чисел 122 и 21.
| Х10 | Х3 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 10 |
| 4 | 11 |
Решение.
122
* 21
122
+1021
11102
Пример 2.1.14. Найти произведение в восьмеричной системе счисления
чисел 706 и 52.
Решение.
706
* 52
1614
+ 4336
45174
Пример 2.1.15.
Найти произведение в шестнадцатеричной системе счисления чисел 122 и 21.
122
*21
122
+244
2562
Пример 2.1.16. Найти А+В, А-В,
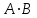и А/В, если А=1446, В=246Решение
| Х10 | Х6 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 10 |
| 7 | 11 |
| 8 | 12 |
| 9 | 13 |
| 10 | 14 |
| 11 | 15 |
| 12 | 20 |
| 13 | 21 |
| 14 | 22 |
| 15 | 23 |
| 16 | 24 |
| 144 + 24 212 | 144 - 24 120 | 144 *24 1104 +332 4424 | 144|24 144 4 0 |
Пример 2.1.17.
Найти произведение в шестнадцатеричной системе счисления чисел 706 и 52.
Решение.
706
*52
Е0С
+231Е
23FEC
Таблица 2.1.2
| Эквиваленты в системах счисления | Эквиваленты в системах счисления | ||||||
| 10 СС | 2 СС | 8 СС | 16 СС | 10СС | 2СС | 8 СС | 16 СС |
| 0 | 0 | 0 | 0 | 11 | 1011 | 13 | В |
| 1 | 1 | 1 | 1 | 12 | 1100 | 14 | С |
| 2 | 10 | 2 | 2 | 13 | 1101 | 15 | D |
| 3 | 11 | 3 | 3 | 14 | 1110 | 16 | Е |
| 4 | 100 | 4 | 4 | 15 | 1111 | 17 | F |
| 5 | 101 | 5 | 5 | 16 | 10000 | 20 | 10 |
| 6 | 110 | 6 | 6 | 17 | 10001 | 21 | 11 |
| 7 | 111 | 7 | 7 | 18 | 10010 | 22 | 12 |
| 8 | 1000 | 10 | 8 | 19 | 10011 | 23 | 13 |
| 9 | 1001 | 11 | 9 | 20 | 10100 | 24 | 14 |
| 10 | 1010 | 12 | А | 21 | 10101 | 25 | 15 |
| Числовые эквиваленты в различных системах счисления | ||||||||
| 10 СС | 2СС | 4СС | 8СС | 16 СС | ||||
| 10 СС | 2СС | 4 СС | 2СС (диада) | 8 СС | 2СС (триада) | 16 СС | 2СС (тетрада) | 4СС (диада) |
| 0 | 0 | 0 | 00 | 0 | 000 | 0 | 0000 | 00 |
| 1 | 1 | 1 | 01 | 1 | 001 | 1 | 0001 | 01 |
| 2 | 10 | 2 | 10 | 2 | 010 | 2 | 0010 | 02 |
| 3 | 11 | 3 | 11 | 3 | 011 | 3 | 0011 | 03 |
| 4 | 100 | 10 | 0100 | 4 | 100 | 4 | 0100 | 10 |
| 5 | 101 | 11 | 0101 | 5 | 101 | 5 | 0101 | 11 |
| 7 | 111 | 13 | 0111 | 7 | 111 | 7 | 0111 | 13 |
| 6 | 110 | 12 | 0110 | 6 | 110 | 6 | 0110 | 12 |
| 8 | 1000 | 20 | 10 00 | 10 | 001 000 | 8 | 1000 | 20 |
| 9 | 1001 | 21 | 10 01 | 11 | 001 001 | 9 | 1001 | 21 |
| 10 | 1010 | 22 | 10 10 | 12 | 001 010 | А | 1010 | 22 |
| 11 | 1011 | 23 | 10 11 | 13 | 001 011 | B | 1011 | 23 |
| 12 | 1100 | 30 | 1100 | 14 | 001 100 | С | 1100 | 30 |
| 13 | 1101 | 31 | 11 01 | 15 | 001 101 | D | 1101 | 31 |
| 14 | 1110 | 32 | 11 10 | 16 | 001 010 | Е | 1110 | 32 |
| 15 | 1111 | 33 | 1111 | 17 | 001 011 | F | 1111 | 33 |
| 16 | 10000 | 100 | 100 00 | 20 | 001 100 | 10 | 0001 0000 | 01 00 |
Таблица сложения в восьмеричной системе счисления
Тема 1.3 Кодирование и обработка чисел
-
Прямой, обратный и дополнительные коды чисел
Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (нуль или единица) перед его старшим числовым разрядом.
Пример_3_.'>Пример__2.'>Пример 1.
| A10=+10 A2=+1010 [A2]П=0:1010; | B10= -15 B2= -1111 [B2]П=1:1111. |
Точечной вертикальной линией здесь отмечена условная граница, отделяющая знаковый разряд от значащих.
Обратный код двоичного числа образуется по следующему правилу. Обратный код положительных чисел совпадает с их прямым кодом. Обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются на инверсные, т.е. нули заменяются единицами, а единицы - нулями.
Пример 2.
| A10=+5 A2=+101 [A2]П=[A2]OK=0:101; | B10= -13 B2= - 1101 [B2]OK=1:0010. |
Свое название обратный код чисел получил потому, что коды цифр отрицательного числа заменены на инверсные. Укажем наиболее важные свойства обратного кода чисел:
-
сложение положительного числа С с его отрицательным значением в обратном коде дает так называемую машинную единицу МЕок= 1: 111... 11, состоящую из единиц в знаковом и значащих разрядах числа; -
нуль в обратном коде имеет двоякое значение. Он может быть положительным - 0: 00...0 и отрицательным числом - 1; 11... 11. Значение отрицательного нуля совпадает с МЕок. Двойственное представление нуля явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.
Дополнительный код положительных чисел совпадает с их прямым кодом. Дополнительный код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей младшего разряда (2° - для целых чисел, 2-k - для дробных).
Пример 3.
| A10=+19 A2=+10011 [A2]П=[A2]OK=[A2]ДК=0:10011; | B10=- 13 В2= -1101 [B2]ДК=[B2]OK+20=1:0010 + 1 =1:0011. |
Укажем основные свойства дополнительного кода:
-
сложение дополнительных кодов положительного числа С с его отрицательным значением дает так называемую машинную единицу дополнительного кода: -
МЕДК=МЕОК+20=10: 00…00,
т.е. число 10 (два) в знаковых разрядах числа;
-
дополнительный код получил такое свое название потому, что представление отрицательных чисел является дополнением прямого кода чисел до машинной единицы МЕдк.
Модифицированные обратные и дополнительные коды двоичных чисел отличаются соответственно от обратных и дополнительных кодов удвоением значений знаковых разрядов. Знак “+” в этих кодах кодируется двумя нулевыми знаковыми разрядами, а “-” - двумя единичными разрядами.
Пример 4.
| A10=9 A2=+1001 [A2]П=[A2]OK=[A2]ДК=0:1001 [A2]МОК=[A2]МДК=00:1001; | B10= -9 B2= -1001 [B2]OK=1:0110 [B2]ДК=1:0111 [B2]МОК=11:0110 [B2]МДК=11:0111. |
Целью введения модифицированных кодов являются фиксация и обнаружение случаев получения неправильного результата, когда значение результата превышает максимально возможный результат в отведенной разрядной сетке машины. В этом случае перенос из значащего разряда может исказить значение младшего знакового разряда. Значение знаковых разрядов “01” свидетельствует о положительном переполнении разрядной сетки, а “10” - об отрицательном переполнении. В настоящее время практически во всех моделях ЭВМ роль удвоенных разрядов для фиксации переполнения разрядной сетки играют переносы, идущие в знаковый и из знакового разряда.
1 2 3 4 5 6 7 8 9 ... 14
Арифметические операции над числами с фиксированной точкой
Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код. Пусть числа A=>O и В=>О, тогда операция алгебраического сложения выполняется в соответствии с табл. 2.3.
Таблица 2.3
Таблица преобразования кодов при алгебраическом сложении
| Требуемая операция | Необходимое преобразование |
| А+В А-В -А+В -А-В | А+В А+(-В) (-А)+В (-А)+(-В) |
Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа. Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с табл. 2.2. При выполнении сложения цифр необходимо соблюдать следующие правила.
-
Слагаемые должны иметь одинаковое число разрядов. Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа. -
Знаковые разряды чисел участвуют в сложении так же, как и значащие. -
Необходимые преобразования кодов производятся с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу. -
При образовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом. При использовании ДК единица переноса теряется. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые.
Пример 4. Сложить два числа А10=7 В10=16
A2=+11=+0111;
B2=+1000=+10000.
Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:
[A2]П=[A2]OK=[A2]ДК=0: 00111;
[B2]П
=[B2]OK=[B2]ДК= 0: 10000.
Сложение в обратном или дополнительном коде дает один и тот же результат
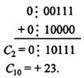
Обратим внимание, что при сложении цифр отсутствуют переносы в знаковый разряд и из знакового разряда, что свидетельствует о получении правильного результата.
Пример 5. Сложить два числа А10 = + 16 В10 = —7 в ОК и ДК. В соответствии с табл. 2.3 должна быть реализована зависимость А+(-В), в которой второй член преобразуется с учетом знака
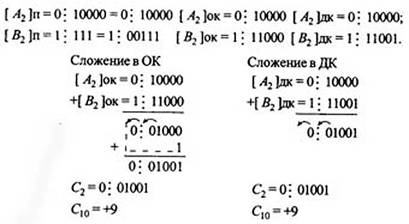
При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда (см.п.4 правил). В случае ДК этот перенос игнорируется.
Тема 1.4 Основы алгебры логики
-
Логические операции
В математической логике определены следующие шесть основных логических операций (связок), которые первоначально были введены еще в классической логике Аристотелем и наиболее часто присутствуют в разнообразных системах программирования:
-
инверсия (логическое отрицание), -
конъюнкция {логическое произведение), -
дизъюнкция (нестрогое логическое сложение), -
исключающая дизъюнкция (строгое логическое сложение), -
импликация (логическое следствие), -
эквиваленция.
Для обозначения этих логических операций применяются следующие символические обозначения (здесь приведены различные обозначения, встречающиеся в литературе по математической логике и в языках программирования):
1)
, 
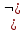, NOT — обозначает логическое НЕ,-
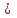&., •, AND - обозначает логическое И, -
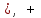, OR - обозначает логическое ИЛИ, -
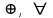, XOR - обозначает исключающее логическое ИЛИ, -
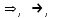, IMP - обозначает импликацию, -
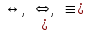, EQV - обозначает эквиваленцию.
Рассмотрим основные логические операции логики высказываний.
