Файл: Курс лекций по дисциплине Цифровая схемотехника для специальности.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 105
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Некоторые, из приведенных в таблице функций уже рассматривались ранее. Так например, функции F0 и F15 являются тождественно постоянными - F0(A,B) = 0, Fl5(A,B)- 1 (логическими константами). F1(A.B)=AB - является конъюнкцией логических переменных А и В, F7(A,B) = А + В - дизъюнкцией, F9(A, B) = А
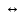 В - эквиваленцией, a F13(A,B) = А
В - эквиваленцией, a F13(A,B) = А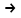 В импликацией. Функции F12, Fl0, F6, F3 и F14 являются, соответственно, отрицанием А, отрицанием В исключающей дизъюнкцией А и В, стрелкой Пирса и штрихом Шеффера.
В импликацией. Функции F12, Fl0, F6, F3 и F14 являются, соответственно, отрицанием А, отрицанием В исключающей дизъюнкцией А и В, стрелкой Пирса и штрихом Шеффера.Совокупность фиксированных значений истинности и аргументов A1,A2,A3,....An принято обозначать в виде последовательности нулей и единиц.
например 001 …110. Такие последовательности нулей и единиц называют наборами и говорят: что функция F(A*1,A*2,A*3,....A*n) рассматривается на конкретном наборе (A*1,A*2,A*3,....A*n), где А*n есть либо ноль либо единица, а индекс указывает на то, что из всевозможных наборов рассматривается n- ая комбинация.
По своему виду конкретные наборы соответствуют n-разрядной записи числа в двоичной системе счисления. Поэтому конкретные наборы часто представляют в виде двоичных или десятичных их числовых эквивалентов. Возможным наборам значений для некоторой логической функции от двух логических переменных А и В соответствуют четыре двоичных числа - 00, 01, 10 и 11 или их десятичных эквиваленты - 0, 1, 2 и 3. Для функции от трех логических переменных соответствуют восемь двоичных чисел - 000, 001, 010 011, 100, 101, 110, 111 или десятичных числа - 0, 1, 2 , 3. 4, 5, 6 и 7. Дли введенных логических функций от F0 до F3, представленных в первой таблице, и от F0 до F15, представленных во второй таблице, их десятичный индекс соответствует десятичному эквиваленту распределения их двоичных значений, если их записать в виде двоичных чисел сверху вниз.
Пример 1
Какие из приведенных ниже выражений являются формулами логики высказываний, а какие нет?
1.
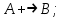 2.
2. 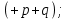 3.
3. 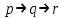 ; 4.
; 4. 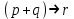
Решение.
Здесь выражения под номерами 1, 2 не являются формулами логики высказываний (в 1 - нельзя записать подряд две логические операции, в 2 - высказывание не может начинаться с символа логического сложения). Формулами логики высказываний является формулы под номерами 3 и 4.
Иногда вводят в рассмотрение понятие "подформулы". Если F- формула, а - какая-либо ее связная часть, которая сама является формулой, то называется подформулой формулы F. Понятие подформулы не следует путать с понятием связной части формулы. Связная часть формулы - это часть формулы, которая выписана из нее без пропусков. Например, в формуле
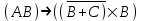 есть следующие подформулы А, В, С, АВ,
есть следующие подформулы А, В, С, АВ, 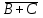 ,
,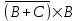 . Никаких других подформул данная формула не имеет. Выражение
. Никаких других подформул данная формула не имеет. Выражение 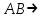 является частью формулы, но подформулой не является.
является частью формулы, но подформулой не является. 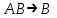 также не является подформулой, поскольку не является се связной частью. Главной подформулой формулы Fназывается такая ее подформула, которая не является частью никакой другой подформулы формулы F. Например, формула
также не является подформулой, поскольку не является се связной частью. Главной подформулой формулы Fназывается такая ее подформула, которая не является частью никакой другой подформулы формулы F. Например, формула 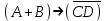 имеет две главные подформулы (А + В) и
имеет две главные подформулы (А + В) и 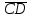 .
.Логические формулы допускают различные тождественные преобразования с целью их упрощения или придания им более удобного для применения вида. Запись формулы часто можно упростить:
1) Внешние скобки можно опустить;
2) Если подформула имеет вид
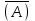 , то скобки можно опустить. Таким образом, правила опускания скобок аналогичны соответствующим правилам опускания скобок в арифметике и алгебре, нужно лишь учитывать приоритетность выполнения логических операции.
, то скобки можно опустить. Таким образом, правила опускания скобок аналогичны соответствующим правилам опускания скобок в арифметике и алгебре, нужно лишь учитывать приоритетность выполнения логических операции.Пример 2. Опустить лишние скобки в формуле
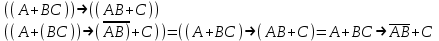
Пример 3. Восстановите опушенные скобки в формуле
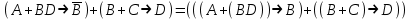
Для каждой формулы алгебры логики может быть построена соответствующая таблица истинности. Задача построения таблицы истинности для формулы, состоящей из n переменных, есть задача построения двоичной функции (Булевой функции), соответствующей данной формуле.
Алгоритм построения таблиц истинности
Пусть задана логическая формула, и нам надо построить ее таблицу истинности. Для построения таблицы истинности этой формулы необходимо выполнить следующие действия:
-
Определить количество переменных, входящих в формулу и составить таблицу всевозможных значений переменных (наборов, иногда также говорят - оценок переменных), от которых зависит данная формула. Конкретные наборы можно рассматривать как числа в двоичной системе счисления и их удобно располагать в порядке возрастании от 0 до 2n -1, если количество переменных равно n. -
Провести анализ построения этой формулы с учетом расположения скобок и приоритетности порядка выполнения логических операций. Выписать саму формулу, затем ее главные подформулы, затем под каждой подформулой снова выпишем главные подформулы и т.д. Количество столбцов в таблице должно быть равно сумме количества простых переменных и выделенных подформул плюс один столбец отводится на саму формулу. Общее количество строк должно быть на единицу больше, то есть 2n +1. Одна строка добавляется для записи переменных, всех подформул и самой формулы. -
Поэтапно сверху вниз строить таблицу истинности, двигаясь слева направо, для всех подформул (лучше по порядку их выполнения). В результате получим таблицу истинности для исходной формулы.
Пример
Построить таблицу истинности для логической функции
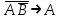 .
.| Оценка | А | В | 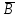 | 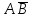 | 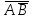 | 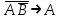 |
| m1 | 0 | 0 | 1 | 0 | 1 | 0 |
| m2 | 0 | 1 | 0 | 0 | 1 | 0 |
| m3 | 1 | 0 | 1 | 1 | 0 | 1 |
| m4 | 1 | 1 | 0 | 0 | 1 | 1 |
Отношения между формулами алгебры логики
Из полученной выше таблицы истинности видно, что истинностные значения формулы
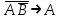 точно совпадают со значением логической переменной А. Они либо одновременно ложны, либо одновременно истинны. Такие формулы называются равносильными или эквивалентными. Равносильные формулы могут содержать различное количество логических переменных. Даже в рассмотренном примере, левая часть зависит от двух логических переменных - А и В, а правая часть только от одной логической переменной А. Важно, чтобы формулы, которые называются равносильными, имели одинаковые значения при одинаковых наборах логических переменных по тем переменным, от которых они зависят. Для обозначения равносильности пользуются обычно знаком равенства:
точно совпадают со значением логической переменной А. Они либо одновременно ложны, либо одновременно истинны. Такие формулы называются равносильными или эквивалентными. Равносильные формулы могут содержать различное количество логических переменных. Даже в рассмотренном примере, левая часть зависит от двух логических переменных - А и В, а правая часть только от одной логической переменной А. Важно, чтобы формулы, которые называются равносильными, имели одинаковые значения при одинаковых наборах логических переменных по тем переменным, от которых они зависят. Для обозначения равносильности пользуются обычно знаком равенства: 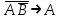 =А
=АУпрощение логических формул может также проводиться но правилу подстановки. Если в формуле есть какая-либо подформула, которая равносильна другой формуле, то эту подформулу можно заменить равносильной. Для такой подстановки используются таблицы истинности, а на практике наиболее часто применяются законы математической логики.
С помощью таблиц истинности для формул, имеющих небольшое количество переменных и число логических операций, можно достаточно просто проверить равносильность формул.
Пример
Проверить равносильность формул с помощью таблиц истинности:
1.
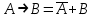
2.
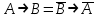
3.
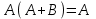
4.
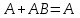
5.
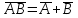
6.
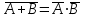
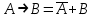 | | 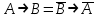 | |||||||||
| А | В | | 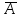 | 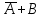 | | А | В | | 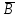 | 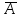 | 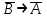 |
| 0 | 0 | 1 | 1 | 1 | | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | | 1 | 1 | 0 | 0 | 0 | 1 |
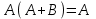 | | 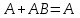 | ||||||
| А | В | А+В | 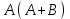 | | А | В | АВ | А+АВ |
| 0 | 0 | 0 | 0 | | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | | 1 | 1 | 1 | 1 |
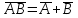 | | 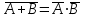 | ||||||||||||
| А | В | АВ | 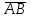 | 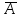 | 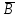 | 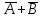 | | А | В | А+В | 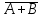 | 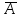 | 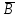 | 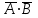 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | | 1 | 1 | 1 | 0 | 0 | 0 | 0 |


