Файл: Фрактальная модель динамики численности народонаселения.docx
Добавлен: 28.03.2024
Просмотров: 20
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования Российской Федерации
Тверской государственный университет
Реферат на тему:
«Фрактальная модель динамики численности народонаселения»
Исполнитель: студент группы М-11М
Фёдоров А.В.
Тверь 2023
Оглавление
Введение
-
Анализ подходов к построению математических моделей динамики численности населения.
-
Уравнения демографической динамики.
-
Построение и реализация фрактальной модели динамики численности народонаселения.
Заключение
Список использованных источников
Введение
В настоящее время существует достаточно большое количество математических моделей для прогноза динамики численности населения. При построении данных математических моделей, различные авторы используют свои идеи и принципы их построения. Так, например, анализируя динамику народонаселения всей Земли, часто используют принцип замкнутой системы. Данный принцип используется, когда на систему не действуют внешние факторы, а только те, что используются в модели. Принцип замкнутой системы используют не только для описания численности всей Земли, но и для страны, отдельного региона и т.д. Но помимо не включенных факторов, в таких системах не используют показатели миграции. Ведь учет миграционных процессов в модели динамики численности соответствует принципу открытой системы. Другие используют биологические модели, где динамика численности популяции определяется процессами воспроизводства. В таких моделях факторы, влияющие на демографические процессы (например, уровень жизни населения и т.д.), учитываются введением соответствующих коэффициентов модели, характерных только для биологических популяций (такие как, рождаемость, смертность и т.д.). Иногда в таких моделях динамика численности (рождаемость и смертность) учитывается не коэффициентами, а функциями.
В моделях мировой динамики используют также принцип ограниченности ресурсов. В необходимы для описания последствий роста численности населения, нехватки пищи или ресурсов, загрязнение окружающей среды. Первая из широко известных математических моделей роста народонаселения была предложена Т.Мальтусом в XIX веке. Согласно ей численность народонаселения N изменяется со временем как eαt, где коэффициент α получил название мальтузианского коэффициента. По-видимому, такой рост народонаселения соответствует неограниченным территории и ресурсам.
-
Анализ подходов к построению математических моделей динамики численности населения
В настоящее время численность населения Земли составляет 6,8 млрд. человек. Скорость роста народонаселения является одним из важнейших количественных показателей, характеризующих качество условий проживания человечества на Земле. Так в 20 веке количество людей выросло в четыре раза. Причем в городах живет 47% населения, а в деревнях – 53%. По многим прогнозам ожидается, что примерно в 2030 г. численность населения Земли достигнет 8 млрд. В первую очередь, рост народонаселения прогнозируется в городах.
Необходимо отметить и явление старения населения Земли. Быстрее всего увеличивается численность людей старше 80 лет. По проведенным оценкам ООН, в настоящее время ежегодно численность населения увеличивается на 1,2 %. На развивающиеся страны приходится 97 роста. Лидерами прироста являются Индия, Китай, Пакистан, Нигерия, Бангладеш, Индонезия. Из развитых стран высокий уровень рождения сохраняется лишь в США. Эта страна занимает 7 место в мире по темпам прироста численности населения. Иммигранты обеспечивают 80% этого роста. В Европе численность населения сокращается несмотря на существенную иммиграцию. В ряде работ [17 - 27] рассматривается вероятность того, что “пик” (численности человечества) будет достигнут уже при жизни нынешнего поколения, после чего начнется неуклонное ее снижение. Такой возможный ход истории получил отражение в изданиях ООН, отличающихся взвешенным подходом. Так в прогнозе комитета ООН по народонаселению “The 1996 Revision” наряду с “высшим” и “средним” присутствует и “низкий” вариант, согласно которому уже после 2040 г. при “нормальном” развитии событий, исключающем войны, голод и крупные эпидемии, рост численности прекратится, после чего начнется депопуляция мира. По этому сценарию народонаселение в 2040 году будет составлять 7,7 млрд. человек. Но уже за период с 2040 по 2050 г.г. человечество сократиться на 8 млн. человек. Далее оно будет сокращаться на 25% с каждым поколением [28].
Многообразие сценариев динамики народонаселения, опирающихся на различные механизмы, влияющие на демографические процессы, ставит вопрос о построение модели роста народонаселения, описывающих этот процесс и независящей от всевозможных допущений и предположений.
В настоящее время численность населения Земли составляет 6,8 млрд. человек. Скорость роста народонаселения является одним из важнейших количественных показателей, характеризующих качество условий проживания человечества на Земле. Так в 20 веке количество людей выросло в четыре раза. Причем в городах живет 47% населения, а в деревнях – 53%. По многим прогнозам ожидается, что примерно в 2030 г. численность населения Земли достигнет 8 млрд. В первую очередь, рост народонаселения прогнозируется в городах.
Первая из широко известных математических моделей роста народонаселения была предложена Т.Мальтусом в XIX веке. Согласно ей численность народонаселения N изменяется со временем как eαt, где коэффициент α получил название мальтузианского коэффициента. По-видимому такой рост народонаселения соответствует неограниченным территории и ресурсам.
Но в 1960 г. X. фон Ферстер, П. Мора и JI. Амиот опубликовали в журнале Science сообщение [14] что между 1 и 1958 г. н.э. динамика численность народонаселения мира (N) может быть с необычайно высокой точностью описана при помощи другого соотношения:
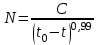
С. фон Хернером (von Hoerner 1975) [14] и С. П. Капицей (1992, 1996, 1999) [8, 13, 15] было показано, это уравнение имеет смысл использовать в следующем аппроксимированном виде
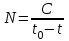
Графиком данного уравнения является гипербола; описываемый этим уравнением закон роста обозначается как «гиперболический».
В этом случае численность народонаселения растет по гиперболическому закону росла по гораздо более быстрому гиперболическому закону, а время t0
2025 год . Этот закон также получил название режима с обострением.
-
Анализ подходов к построению математических моделей динамики численности населения. -
Уравнения демографической динамики. -
Построение и реализация фрактальной модели динамики численности народонаселения.
Анализ подходов к построению математических моделей динамики численности населения
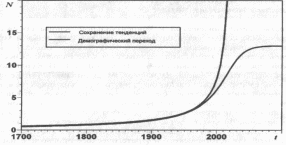
Согласно этой модели в 2025 году нас ждет демографический взрыв, когда численность народонаселения должна вырасти почти мгновенно до очень больших значений, что практически нереально.
Рис 1.
Как видно из Рис. 1 реальный рост народонаселения не соответствует как экспоненциальному, так и гиперболическому законам. Кривая народонаселения с 1950 года разбивается на 3 участка, на каждом из которых с высокой степенью точности численность народонаселения растет линейно.
Характер данного процесса ближе всего соответствует описанию в рамках мультифрактальной динамики.
В данной работе мы предлагаем такую модель, которая основана на фрактальном подходе. Эта модель представляется более надежной по сравнению с другими. Она мало зависит от деталей функционирования рассматриваемой системы, устройство которой и численные параметры ее нам недостаточно известны.
-
Уравнения демографической динамики.
В основе уравнений демографической динамики лежит, как правило, соотношение между скоростью изменения тренда численности народонаселения
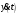 и трендом численности народонаселения
и трендом численности народонаселения 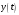 (непрерывной и гладкой функции апроксимирующей данные по численности народонаселения). Из многочисленных демографических уравнений приведем некоторые их них:
(непрерывной и гладкой функции апроксимирующей данные по численности народонаселения). Из многочисленных демографических уравнений приведем некоторые их них:  (Мальтус [2]),
(Мальтус [2]), 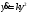 (Х. фон Ферстер [3], С. фон Хернер [4], Капица С.П. [5]),
(Х. фон Ферстер [3], С. фон Хернер [4], Капица С.П. [5]), 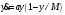 (Ферхюльст [6]), уравнения со стабилизацией численности народонаселения (Капица С.П. [7], А.В. Подлазов [8], С.В. Цирель [9], Коротаев А.В., Малков А.С., Халтурина Д.А. [10], Акаев А.А., Садовничий В.А. [11]), уравнения мультифрактальной динамики (А.Н. Кудинов и др. [12]). Рассмотренные примеры говорят о многообразии типов уравнений, используемых для решения конкретных задач в демографии.
(Ферхюльст [6]), уравнения со стабилизацией численности народонаселения (Капица С.П. [7], А.В. Подлазов [8], С.В. Цирель [9], Коротаев А.В., Малков А.С., Халтурина Д.А. [10], Акаев А.А., Садовничий В.А. [11]), уравнения мультифрактальной динамики (А.Н. Кудинов и др. [12]). Рассмотренные примеры говорят о многообразии типов уравнений, используемых для решения конкретных задач в демографии.Для описания демографической динамики в данной работе предлагается использовать новое демографическое уравнение:
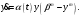 (1)
(1)Преобразованием
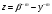
уравнение (1) сводится к уравнению Мальтуса
 с мальтузианским коэффициентом
с мальтузианским коэффициентом  и поэтому его интегрирование не вызывает затруднений.
и поэтому его интегрирование не вызывает затруднений.Уравнение демографической динамики (1) содержит три независимых параметра
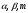 , выбором которых можно описать гораздо больше демографических сценариев по сравнению с другими уравнениями, зависящими от одного или двух параметров, и поэтому его вполне можно отнести к классу реалистических демографических уравнений. Полагая
, выбором которых можно описать гораздо больше демографических сценариев по сравнению с другими уравнениями, зависящими от одного или двух параметров, и поэтому его вполне можно отнести к классу реалистических демографических уравнений. Полагая  , получаем из (1) уравнение Мальтуса, при
, получаем из (1) уравнение Мальтуса, при 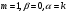 - уравнение С. фон Хернера, С.П. Капицы, а при
- уравнение С. фон Хернера, С.П. Капицы, а при  - уравнение Ферхюльста.
- уравнение Ферхюльста.В уравнении (1) параметры
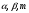 являются фундаментальными демографическими параметрами. Определим демографический период, как временной интервал, на котором демографические параметры постоянны, и значения которых определяются совокупностью экономических, социальных, политических и других факторов интересующей нас территориальной структуры. На стыке демографических периодов параметры
являются фундаментальными демографическими параметрами. Определим демографический период, как временной интервал, на котором демографические параметры постоянны, и значения которых определяются совокупностью экономических, социальных, политических и других факторов интересующей нас территориальной структуры. На стыке демографических периодов параметры 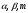 естественно меняются скачками. А переход из одного демографического периода в другой имеет смысл демографического фазового перехода. При этом будем полагать, что численность народонаселения
естественно меняются скачками. А переход из одного демографического периода в другой имеет смысл демографического фазового перехода. При этом будем полагать, что численность народонаселения  и скорость его изменения
и скорость его изменения  являются в точке демографического фазового перехода
являются в точке демографического фазового перехода  непрерывными функциями времени
непрерывными функциями времени  . Пусть при t=0 величина
. Пусть при t=0 величина  и
и 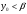 ,
,  , тогда
, тогда  - предельное значение численности народонаселения при его росте. Если же
- предельное значение численности народонаселения при его росте. Если же 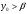 ,
, 
, тогда
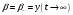 - предельное значение численности народонаселения при его уменьшении. Величина и знак параметра
- предельное значение численности народонаселения при его уменьшении. Величина и знак параметра  определяют, прежде всего, скорость роста или уменьшения численности народонаселения. Параметр
определяют, прежде всего, скорость роста или уменьшения численности народонаселения. Параметр 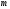 в уравнении (1) является степенным фактором и существенно определяет характер его решения. Поэтому естественно
в уравнении (1) является степенным фактором и существенно определяет характер его решения. Поэтому естественно 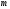 назвать демографическим индексом, в значительной степени определяющим эволюцию демографического процесса.
назвать демографическим индексом, в значительной степени определяющим эволюцию демографического процесса.Для описания мировой демографической динамики будем использовать предложенное нами уравнение (1), а параметры
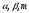 будем вычислять из условия наилучшего согласия с данными по народонаселению Мира с РХ по настоящее время [1], что принципиально отличает данный метод от других подходов. Таким образом, используя данные [1], мы учитываем все многообразие демографических факторов (экономические, политические, социальные, культурные, биологические и др.), определяющих рост народонаселения Земли.
будем вычислять из условия наилучшего согласия с данными по народонаселению Мира с РХ по настоящее время [1], что принципиально отличает данный метод от других подходов. Таким образом, используя данные [1], мы учитываем все многообразие демографических факторов (экономические, политические, социальные, культурные, биологические и др.), определяющих рост народонаселения Земли.Представим демографические данные на Рис. 2 с РХ по настоящее время. Здесь и далее величины
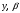 мы будем измерять в млрд. человек.
мы будем измерять в млрд. человек.
Рис. 2. Зависимость численности
народонаселения Мира от времени
с РХ по 2017 год.

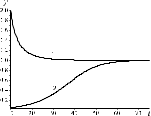

Рис. 3. Графики решения уравнения (1).
Из данных по динамике численности народонаселения Земли [1] следует, что можно выделить за временной промежуток в 2017 лет качественно два периода: I-й период с РХ до середины 1960-х годов, на котором наблюдается увеличение скорости роста народонаселения, II-й период, начиная с середины 60-х и по настоящее время, характеризуется уже замедлением скорости роста народонаселения Земли. Ранее на возможный демографический переход после 1965 года указывал С.П. Капица [7].
Естественно искать решения уравнения (1) в виде двух различных функций

и
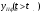 с различными значениями демографических параметров
с различными значениями демографических параметров  . В точке фазового перехода
. В точке фазового перехода 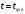 должны выполняться условия непрерывного перехода от первого демографического перехода ко второму:
должны выполняться условия непрерывного перехода от первого демографического перехода ко второму: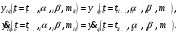
3. Построение и реализация фрактальной модели динамики численности народонаселения.
Численность народонаселения будем измерять в млрд. человек, а время – в годах. Скорость роста народонаселения обозначим

 и она измеряется в
и она измеряется в 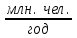

Будем предполагать, что динамика народонаселения является мультифрактальной динамикой. Это означает, что весь промежуток времени наблюдения можно разбить на промежутки, на каждом из которых она имеет определенное значение фрактальной размерности
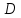
 . На этих участках скорость роста народонаселения
. На этих участках скорость роста народонаселения 
 (тангенс угла наклона линейного тренда) согласно нашей модели [29] является функцией
(тангенс угла наклона линейного тренда) согласно нашей модели [29] является функцией 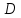
 , которая является решением кубического уравнения
, которая является решением кубического уравнения
 (2).
(2).В этом уравнении для функции
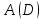
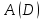 , мы выбираем следующее аналитическое представление:
, мы выбираем следующее аналитическое представление: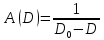
 при
при