Файл: Фрактальная модель динамики численности народонаселения.docx
Добавлен: 28.03.2024
Просмотров: 21
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 , а при
, а при 


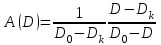 .
.Параметры модели

 и
и  выбираются из наилучшего согласия с опытными данными. В случае
выбираются из наилучшего согласия с опытными данными. В случае 
 членом с
членом с 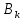
 можно пренебречь, как это нами уже отмечалось ранее, соответственно справедливо линейное приближение:
можно пренебречь, как это нами уже отмечалось ранее, соответственно справедливо линейное приближение:
 (3).
(3).Стандартной заменой уравнение (2) можно упростить.

 . График зависимости
. График зависимости 
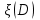 приведен на Рис. 4 и 5 для
приведен на Рис. 4 и 5 для 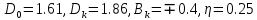
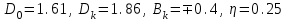 .
.








Dk
D
Db
ξ(D)
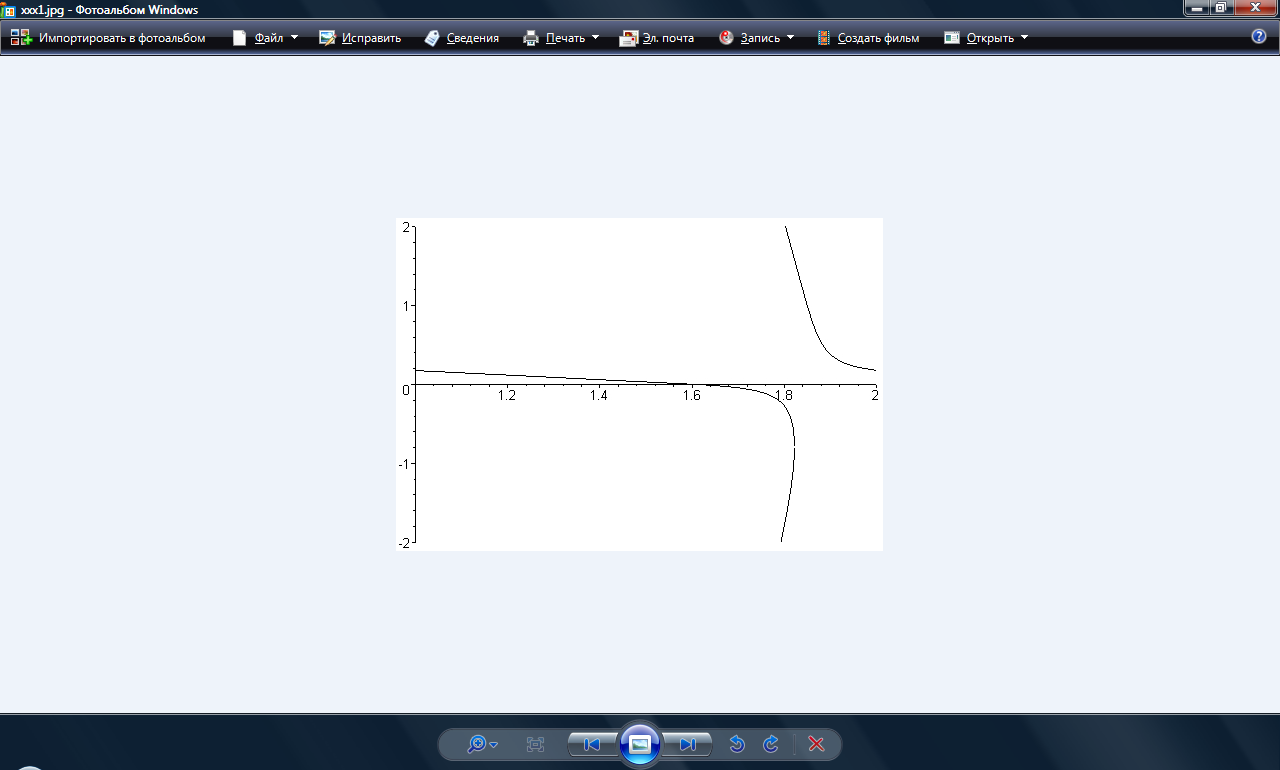
Рис.4 График зависимости

 при
при 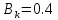
 .
.





ξ(D)
Dk
Db
D
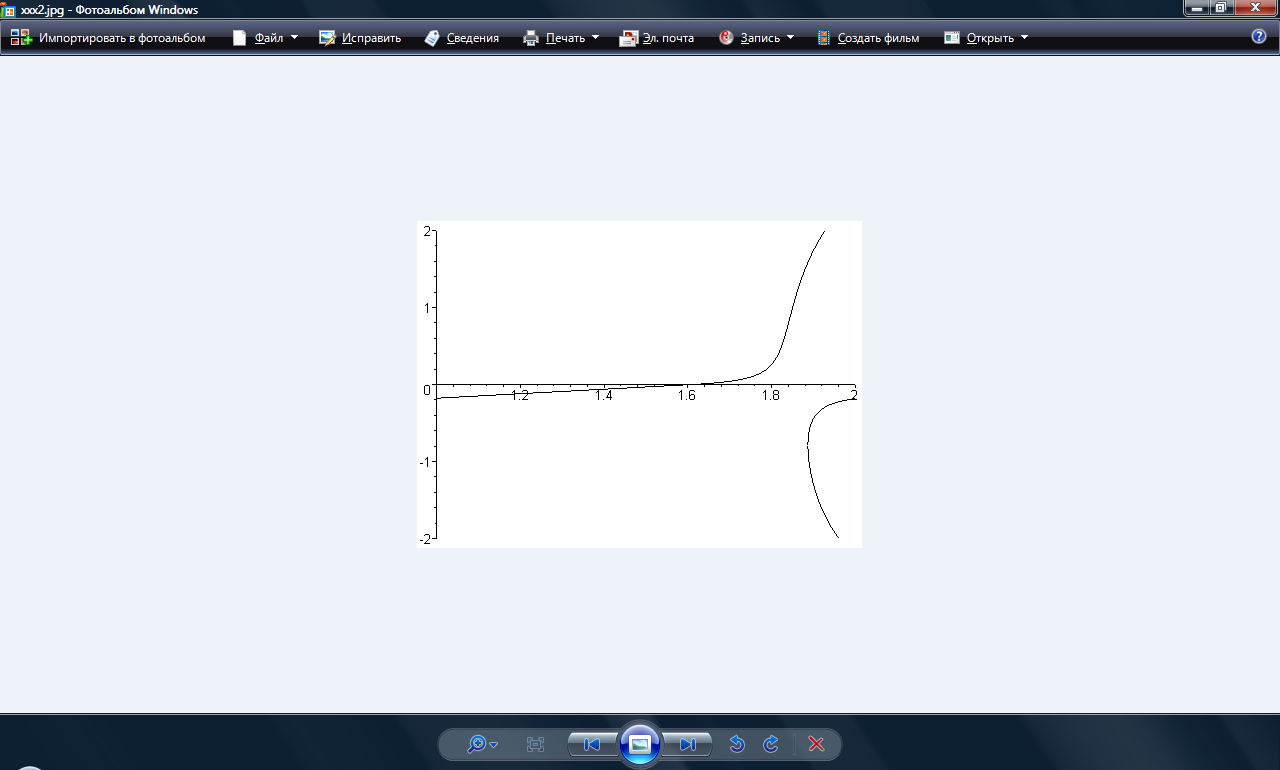
Рис.5 График зависимости

 при
при 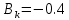
 .
.Из Рис. 4 и 5 следует наличие в данной модели трех характерных точек

 . В точке
. В точке 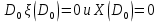

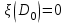 и
и 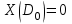 . В этой точке скорость роста равна нулю и мы имеем статистическую ситуацию. Численность народонаселения для этого значения
. В этой точке скорость роста равна нулю и мы имеем статистическую ситуацию. Численность народонаселения для этого значения 
 стабилизируется и равна константе. При небольшом превышении
стабилизируется и равна константе. При небольшом превышении 
 значение
значение 
 будет отрицательно и численность народонаселения линейно начинает сокращаться.
будет отрицательно и численность народонаселения линейно начинает сокращаться.
Критическая точка

 соответствует условию
соответствует условию 
 и становится определяющей нелинейная зависимость
и становится определяющей нелинейная зависимость 
 от
от 
 . В точке
. В точке 


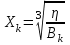 при
при 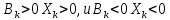
 и
и 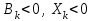 . Это значит, что в критической точке в первом случае имеет место рост народонаселения, а во втором случае - его убывание. При достаточно малых
. Это значит, что в критической точке в первом случае имеет место рост народонаселения, а во втором случае - его убывание. При достаточно малых 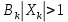

 и возникает или быстрый рост или быстрое убывание народонаселения в этой точке.
и возникает или быстрый рост или быстрое убывание народонаселения в этой точке.Точка бифуркации

 находится из условия:
находится из условия:
 (3).
(3).Отсюда следует значение

 :
:
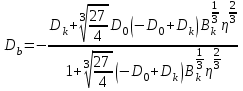 (4)
(4)и сдвиг точки бифуркации от критической точки

 при
при 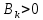

происходит влево, а при

 - вправо. В точке
- вправо. В точке 
 имеются два вещественных корня
имеются два вещественных корня 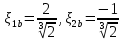
 , которые имеют разные знаки. Если
, которые имеют разные знаки. Если 
 , то
, то 
 .
.Таким образом, в точке

 может иметь место, как рост народонаселения, так и убывание народонаселения. Причем скорость роста в два раза превосходит скорость убывания.
может иметь место, как рост народонаселения, так и убывание народонаселения. Причем скорость роста в два раза превосходит скорость убывания.В случае
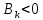
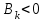 картина наблюдается обратная.
картина наблюдается обратная.С учетом выявленных трендовых периодов были рассчитаны параметры модели народонаселения, которые приведены в таблице 1.
Таблица 1. Параметры модели с кусочно-линейным трендом
| i | 1 | 2 | 3 |
 | 12 | 20 | 29 |
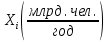 | 49,804 | 73,614 | 80,872 |
| | | | |
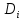 | 1,41 | 1,33 | 1,29 |
 | 1,61 | ||
  |  | ||
Так как значения
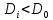 , то используем линейное приближение
, то используем линейное приближение 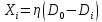 и получим расчетные значения
и получим расчетные значения 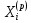 в
в 
 :
: 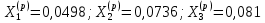 . Разности расчетных и
. Разности расчетных и фактических значений
фактических значений  составляют не более 2% [13].
составляют не более 2% [13].Учитывая опыт моделирования, выберем
 ,
, 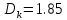 а значение
а значение  вычислим по следующей формуле [13]:
вычислим по следующей формуле [13]: 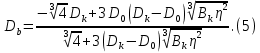
 Подставив в формулу (4) значения
Подставив в формулу (4) значения  ,
,  ,
,  и
и  получим
получим 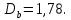
Анализ рассчитанных параметров фрактальной модели показал следующее.
1. Коэффициент линейного тренда во втором периоде увеличился на 48% по сравнению с первым, а в третьем – всего на 10% по сравнению со вторым.
2. Фрактальная размерности кривой народонаселения во втором периоде уменьшилась на 6% по сравнению с первым, а в третьем – всего на 3% по сравнению со вторым. Тенденция к уменьшению фрактальной размерности соответствует увеличению скорости роста народонаселения.
3. Значения
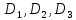 намного меньше значения
намного меньше значения  соответствующего нулевой скорости роста народонаселения. По классификации, приведенной в [16], процесс роста народонаселения в рассматриваемые периоды является монотонным процессом I типа.
соответствующего нулевой скорости роста народонаселения. По классификации, приведенной в [16], процесс роста народонаселения в рассматриваемые периоды является монотонным процессом I типа. 4. Значения фрактальных размерностей