еще дальше находятся от критических значений и , чем от , что указывает на стабильный рост народонаселения. И, следовательно, в ближайшее время катастрофических изменений темпа роста народонаселения не ожидается.

Для анализа роста народонаселения в модели мультифрактальной динамики с нелинейным трендом рассчитаем числовые значения 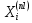и ширину трендовых каналов для трех участков. Эти значения приведены в таблице 2.

Таблица 2. Параметры модели с нелинейным трендом

i	1	2	3
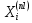	0,0235	0,0071	-0,0128
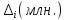	9,7581	10,1557	9,2046

Аппроксимация графика народонаселения нелинейным трендом приведена на рис. 6.



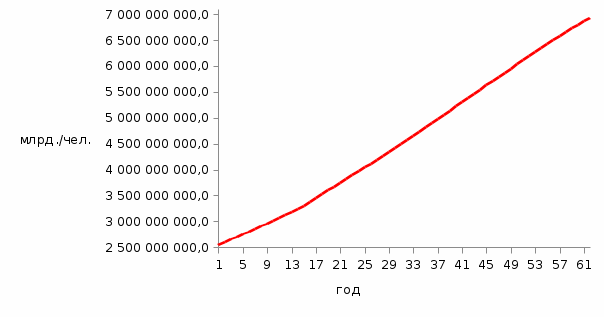
Рис.6. Аппроксимация графика народонаселения нелинейным трендом

Интересно отметить, что ширина трендовых каналов при нелинейном тренде увеличивается (по сравнению с линейным трендом), но все равно остается достаточно малой величиной.
4. Заключение

В данной работе рассматривается новая демографическая математическая модель, которая основана на использовании нового дифференциального уравнения для тренда численности народонаселения, содержащего три параметра, вариативность которых позволяет отразить многообразие сценариев демографической динамики. Их значения вычисляются из условия минимального уклонения расчетной кривой тренда народонаселения Земли в фиксированные моменты времени 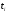от данных ООН по народонаселению Земли. Такой подход позволяет учесть через эти данные влияние основных мировых демографических факторов. Одним из важных результатов нашей модели является возникновение асимптотической стабилизации народонаселения Земли в течение ближайших 100 лет. При этом народонаселение Земли может достигнуть значения порядка 11.57 миллиардов человек. В построенной нами математической модели мировая демографическая история оказалась разделенной на три демографических периода 0, I и II. Показано, что к началу следующего столетия прогнозное население Земли может приблизиться к 11.0257 млрд. человек, а к середине следующего столетия (2150 год) достигнет близого к предельной числености народонасления Земли (11.57 млрд. человек) и сотавит 11.44 млрд. человек.

---

По мнению ряда авторов такое значение численности народонаселение Земли является неустойчивым и впоследствии может начаться процесс уменьшения до 5.2-5.6 млрд. человек [11]. Это обстоятельство вполне объяснимо конечностью ресурсов Земли и технологическим уровнем развития общества, которые необходимы для поддержания жизнедеятельности человечества на приемлемом уровне.
СПИСОК ЛИТЕРАТУРЫ

1. 
   World population. URL: http://countrymeters.info/en/World (accessed 05.12.17).
   
2. 
   Т. Мальтус. Опыт о законе народонаселения. Шедевры мировой экономической мысли. -Петрозаоводск: Петроком, 1993, т. 4, 139 с;
   T. Maltus. Opyt o zakone narodonaseleniia. Shedevry mirovoi ekonomicheskoi mysli. -Petrozavodsk: Petrokom, 1993, t. 4, 139 s.
   
3. 
   H. von Foerster, P. Mora, L. Amiot. Doomsday: Friday, 13 November, A.D. 2026. At this date human population will approach infinity if it grows as it has grown in the last two millennia // Science, 1960, v. 132. p. 1291–1295.
   
4. 
   S.J. von. Hoerner Population Explosion and Interstellar Expansion // Journal of the British Interplanetary Society, 1975, 28: 691-712.
   
5. 
   С.П. Капица. Математическая модель роста народонаселения мира // Матем. моделирование, 1992, т. 4, № 6, с. 65–79;
   S.P. Kapitsa. Matematicheskaia model rosta narodonaseleniia mira // Matem. modelirovanie, 1992, t. 4, № 6, s. 65–79.
   
6. 
   P.F. Verhulst Recherches Mathématiques sur La Loi D’Accroissement de la Population (Mathematical Researches into the Law of Population Growth Increase) // Nouveaux Mémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles, 1845, 18: Art. 1, 1-45.
   
7. 
   С.П. Капица. Феноменологическая теория роста населения Земли // Успехи физ. наук, 1996, т. 166, № 1, с. 63–80;
   S.P. Kapitsa. Fenomenologicheskaia teoriia rosta naseleniia Zemli // Uspekhi fiz. nauk, 1996, t. 166, № 1, s. 63–80.
   

С.П. Капица. Общая теория человечества. Как рос и куда идёт мир человека. Второе издание. -М.: Москва, 2009, 120 с;
S.P. Kapitsa. Obshchaia teoriia chelovechestva. Kak ros i kuda idet mir cheloveka. Vtoroe izdanie. -M.: Moskva, 2009, 120 s.

8. 
   А.В. Подлазов Теоретическая демография как основа математической истории. М.: ИПМ РАН, 2000;
   A.V. PodlazovTeoreticheskaia demografiia kak osnova matematicheskoi istorii. M.: IPM RAN, 2000.
   
9. 
   S.V. Tsirel On the Possible Reasons for the Hyperexponential Growth of the Earth Population // Mathematical Modeling of Social and Economic Dynamics. 2004, p. 367-369.
   
10. 
    А.В. Коротаев, А.С. Малков, Д.А. Халтурина Компактная математическая модель технико-экономического и демографического развития Мир-Системы (1-1973 гг.) // История и синергетика: Математическое моделирование социальной динамики / Ред. С.Ю. Малков и А.В. Коротаев. М.: КомКнига/URSS, 2005, c. 6-48;
    A.V. Korotaev, A.S. Malkov, D.A. KhalturinaKompaktnaia matematicheskaia model tekhniko-ekonomicheskogo i demograficheskogo razvitiia Mir-Sistemy (1-1973 gg.) // Istoriia i sinergetika: Matematicheskoe modelirovanie sotsialnoi dinamiki / Red. S.IU. Malkov i A.V. Korotaev. M.: KomKniga/URSS, 2005, c. 6-48.
    
11. 
    А.А. Акаев, В.А. Садовничий. Математическая модель демографической динамики со стабилизацией численности населения мира вокруг стационарного уровня // Доклады Академии Наук, 2010, т. 435, № 3, с. 320–324;
    A.A. Akaev, V.A. Sadovnichii. Matematicheskaia model demograficheskoi dinamiki so stabilizatsiei chislennosti naseleniia mira vokrug statsionarnogo urovniia // Doklady Akademii Nauk, 2010, t. 435, № 3, s. 320–324.
    
12. 
    А.Н. Кудинов, В.Н. Рыжиков, В.П. Цветков, И.В. Цветков. Тенденции и прогнозирование роста народонаселения в модели мультифрактальной динамики // Нелинейный мир, 2014, т. 12, № 12, с. 53-63;
    A.N. Kudinov, V.N. Ryzhikov, V.P. Tsvetkov, I.V. Tsvetkov. Tendentsii i prognozirovanie rosta narodonaseleniia v modeli multifraktalnoi dinamiki // Nelineinyi mir, 2014, t. 12, № 12, s. 53-63.
    

---

13. Wilson I., Purushothaman R. Dreaming with BRICs: The Path to 2050. Goldman Sachs Global Economics Paper 99. 2003.

14. Foerster H. von, Mora M., Amiot L. Doomsday: Friday, 13 November, A.D. 2026. Science 132: 1291-1295. 1960.

15. Hoerner S.J. von. Population Explosion and Interstellar Expansion. Journal of the British Interplanetary Society 28: 691-712. 1975.

16. Е. Федер. Фракталы. М.: Мир. 1991.

17. А. Кваша. Что такое демография. Москва: Мысль, 1993 год.

18. Д. Шелестов, В. Минаев "Миграционные процессы в России". Журнал "Родина", № 10 за 1996 год.

19. Капица С.П. Сколько людей жило, живет и будет жить на земле.
Очерк теории роста человечества. М.: 1999.

20. Капица С. П. Синергетика и прогноз будущего. М.: 1997

21. Современная демография. Под редакцией А. Я. Кваша, В. А. Ионцевой. М.: Издат-во МГУ 1995.

22. Бондарская Г.А. "Изменение демографического поведения российских семей за 100 лет" / "Мир России", № 4 за 1999 год.

23. Современная демография. / Под ред. А.Я. Кваши, В.А. Ионцева. – М.: Изд-во Моск. ун-та, 1995

24. Борисов В. А. Демография — М.: Издательский дом NOTABENE, 1999, 2001. — 272 с.

25. Медков В. М. Демография: Учебное пособие. Серия «Учебники и учебные пособия». — Ростов-на-Дону: «Феникс», 2002. — 448

26. World Urbanization Prospects: The 1996 Revision.(Review) New York: United Nations, 1998.

27. Капица С.П. Математическая модель роста населения мира// Математическое моделирование. 1992. Т.4, N6. Стр. 65 80.

28. URL: http://www.un.org/esa/population/pubsarchive/catalogue/catrpt1.htm

29. Кудинов А. Н., Сажина О. И., Цветков В. П., Цветков И. В. Фрактальная модель роста народонаселения// Вестник РУДН. Серия Математика. Информатика. Физика. № 2 (2), 2010, с 132-138.

---

Смотрите также файлы

• 2 величина признака, которая чаще всего встречается в данной совокупности.docx

• Лев рубинштейн.pdf

• Сборки в машиностроении.pdf

• Наличие витаминов в детских пакетированных соках.docx

• Наследственности.docx