Файл: Пояснительная записка По образовательной программе 6В03103 Психология По дисциплине.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.03.2024
Просмотров: 91
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, которыми должны характеризоваться группы, т.е. сказуемого группировки.
Статистические группировки и классификации преследуют цели выделения качественно однородных совокупностей, изучения структуры совокупности, исследования существующих зависимостей. Каждой из этих целей соответствует особый вид группировки: типологическая, структурная, аналитическая (факторная).
Типологическая группировка решает задачу выявления и характеристики социально-экономических типов (частных подсовокупностей).
Структурная дает возможность описать составные части совокупности или строение типов, а также проанализировать структурные сдвиги.
Аналитическая (факторная) группировка позволяет оценивать связи между взаимодействующими признаками.
В зависимости от числа положенных в их основание признаков различают простые и многомерные группировки.
Группировка, выполненная по одному признаку, называется простой.
Многомерная группировка производится по двум и более признакам. Частным случаем многомерной группировки является комбинационная группировка, базирующаяся на двух и более признаках, взятых во взаимосвязи, в агрегатные комбинации.
Структурная группировка применяется для характеристики структуры совокупности сдвигов.
Структурной называется группировка, в которой происходит разделение выделенных с помощью технологической группировки типов явлений, однородных совокупностей на группы, характеризующие их структуру по какому-либо варьирующему признаку. Например, группировка населения по размеру среднедушевого дохода. Анализ структурных группировок, взятых за ряд периодов или моментов времени, показывает изменения структуры изучаемых явлений, то есть структурные сдвиги. В изменении структуры общественных явлений отражаются важнейшие закономерности их развития.
Показатель численности групп представлен либо частотой (количеством единиц в каждой группе), либо частотностью (удельным весом каждой группы).
Среди простых группировок особо выделяют ряды распределения.
Ряд распределения –это группировка, в которой для характеристики групп (упорядоченно расположенных по значению признака) применяется один показатель –численность группы. Другими словами, это ряд чисел, показывающий, как распределяются единицы некоторой совокупности по изучаемому признаку.
Ряды, построенные по атрибутивному признаку, называются атрибутивными рядами распределения.
Ряды распределения,
построенные по количественному признаку, называются вариационными рядами.
Примером атрибутивных рядов могут служить распределения населения по полу, занятости, национальности, профессии и т.д.
Примером вариационного ряда распределения могут служить распределения населения по возрасту, рабочих – по стажу работы, заработной плате и т.д.
Вариационные ряды распределения состоят из двух элементов вариантов и частот.
Вариантами называются числовые значения колличественного признака в ряду распределения, они могут быть положительными и отрицательными, абсолютными и относительными.
Частоты – это численности отдельных вариантов или каждой группы вариационного ряда. базисные Сумма всех частот называется объемом совокупности и определяет число элементов всей совокупности.
Вариационные ряды в зависимости от характера вариации подразделяются на дискретные и интервальные.
1.2 Абсолютные и относительные величины
Абсолютные величины – это результаты статистических наблюдений. В статистике в отличие от математики все абсолютные величины имеют размерность (единицу измерения), а также могут быть положительными и отрицательными.
Единицы измерения абсолютных величин отражают свойства единиц статистической совокупности и могут быть простыми, отражая 1 свойство (например, масса груза измеряется в тоннах) или сложными, отражая несколько взаимосвязанных свойств (например, тонно-километр или киловатт-час).
Единицы измерения абсолютных величин могут быть 3 видов:
1 Натуральные – применяются для исчисления величин с однородными свойствами (например, штуки, тонны, метры и т.д.). Их недостаток состоит в том, что они не позволяют суммировать разнородные величины.
2 Условно-натуральные –применяются к абсолютным величинам с однородными свойствами, но проявляющим их по-разному. Например, общая масса энергоносителей (дрова, торф, каменный уголь, нефтепродукты, природный газ) измеряется в т.у.т. – тонны условного топлива, поскольку каждый его вид имеет разную теплотворную способность, а за стандарт принято 29,3 мДж/кг. Аналогично общее количество школьных тетрадей измеряется в у.ш.т. – условные школьные тетради размером 12 листов. Аналогично продукция консервного производства измеряется в у.к.б. – условные консервные банки емкостью 1/3 литра. Аналогично продукция моющих средств приводится к условной жирности 40 %.
3 Стоимостные единицы измерения выражаются в рублях или в иной валюте, представляя собой меру стоимости абсолютной величины. Они позволяют суммировать даже разнородные величины, но их недостаток состоит в том, что при этом необходимо учитывать фактор инфляции, поэтому статистика стоимостные величины всегда пересчитывает в сопоставимых ценах.
1.3 Средние величины и показатели вариации
Средняя величина – это обобщающая характеристика совокупности однотипных явлений по изучаемому признаку.
Выбор средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин:
- арифметическая;
- гармоническая;
- квадратичная;
- геометрическая.
Каждая из них может быть простой и взвешенной. закономерности Перечисленные средние относятся к классу степенных средних и определяются формулой (при различных значениях m):
 , (2)
, (2)
При m=-1 средняя гармоническая < http://chaliev.ru/statistics/srednie- velichiny-i-pokazateli-variatsyi.php>; =0 средняя геометрическая=1 средняя арифметическая < http://chaliev.ru/statistics/srednie-velichiny-i-pokazateli-variatsyi.php>;=2 средняя квадратическая < http://chaliev.ru/statistics/srednie-velichiny-i-pokazateli-variatsyi.php>.
Средняя арифметическая простая – это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:
 , (3)
, (3)
где X – значения величин, для которых необходимо рассчитать среднее значение;
N – общее количество значений X (число единиц в изучаемой совокупности).
Средняя арифметическая взвешенная вычисляется когда варианты встречаются не одинаковое число раз.
2 Практическая часть
Постановка задачи.
Провести статистический анализ данных для переменных X и Y. Найти выборочные средние, дисперсии и среднеквадратические отклонения для X и Y по отдельности.
Найти ковариацию Cov (X, Y).
Найти коэффициент корреляции X и Y.
Найти по выборке уравнение линейной регрессии (Y как функцию X) по методу наименьших квадратов.
Найти по выборке уравнение параболической регрессии второго порядка (Y как функцию X) по методу наименьших квадратов.
Построить графики, изображающие данные выборки и найденные функции регрессии.
Проверить гипотезу о значимости выборочного коэффициента корреляции при заданном уровне значимости альфа =0,001.
Исходные данные.
Нам дана выборка (объемом n=20) зависимости числа Y от числа X.
Таблица 1 – Исходные данные
Статистический анализ данных для переменных X и Y.
Найдем выборочные средние для X и Y по формуле (1):
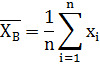 , (4)
, (4)
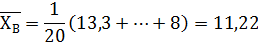 , (5)
, (5)
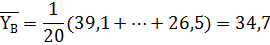 , (6)
, (6)
Найдем выборочные дисперсии для X и Y по формуле (2) и (3):
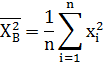 , (7)
, (7)
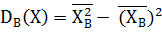 , (8)
, (8)
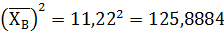 , (9)
, (9)
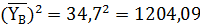 , (10)
, (10)
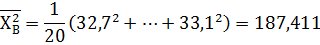 , (11)
, (11)
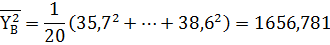 , (12)
, (12)
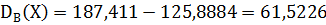 , (13)
, (13)
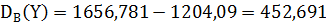 , (14)
, (14)
Найдем выборочные среднеквадратические отклонения для X и Y по формуле (4):
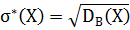 , (15)
, (15)
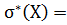 7,843634362, (16)
7,843634362, (16)
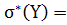 21,27653637, (17)
21,27653637, (17)
Ковариация Cov (X, Y).
Найдем выборочную ковариацию для переменных X и Y по формуле (18):
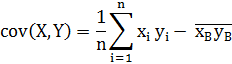 , (18)
, (18)
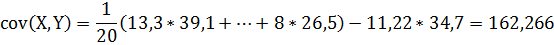 ,(19)
,(19)
Коэффициент корреляции X и Y.
Найдем выборочный коэффициент корреляции для переменных X и Y по формуле (20:
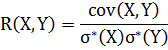 , (20)
, (20)
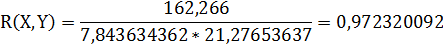 , (21)
, (21)
Уравнение линейной регрессии.
Найдем коэффициенты a и b для уравнения линейной регрессии.
Для нахождения коэффициентов a и b методом наименьших квадратов были посчитаны следующие необходимые параметры:
 , (22)
, (22)
 , (23)
, (23)
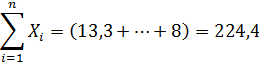 , (24)
, (24)
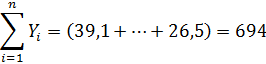 , (25)
, (25)
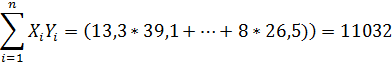 , (26)
, (26)
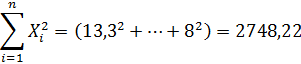 , (27)
, (27)
Тогда коэффициенты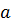 и
и 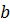 соответственно равны:
соответственно равны:
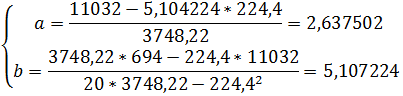 , (28)
, (28)
Таким образом, получаем уравнение линейной регрессии:
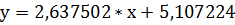 , (29)
, (29)

Рисунок 1 – Линейная регрессия
Гипотеза о значимости выборочного коэффициента корреляции.
Проверим гипотезу о значимости выборочного коэффициента корреляции, для этого вычислим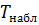 и
и 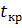 (на уровне значимости равном 0,001).
(на уровне значимости равном 0,001).
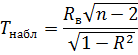 , (30)
, (30)
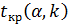 , (31)
, (31)
Получаем:
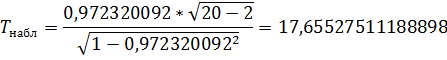 , (32)
, (32)
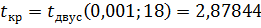 , (33)
, (33)
Поскольку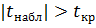 , можно сказать, что выборочный коэффициент корреляции отличается от нуля, а X и Y коррелированы.
, можно сказать, что выборочный коэффициент корреляции отличается от нуля, а X и Y коррелированы.
Заключение
В данной курсовой работе были вычислены основные числовые характеристики выборок по X и Y.
По выборке проведено исследование корреляционной зависимости по выборке. Найдены ковариация и коэффициент корреляции. В результате проведенной работы были закреплены теоретические знания и приобретены практические навыки работы со статистиками, умение находить точечные и интервальные оценки математического ожидания и дисперсии.
Был изучен метод регрессионного анализа, при помощи которого удаётся провести зависимость прожиточного минимума (Y) от заработной платы (X).
1 Статистика : учебное пособие / А. В. Багат и др.; под ред. В. М. Симчеры. – М. : Финансы и статистика, 2011.
2 Гусаров В. М. Теория статистики : учебное пособие для вузов / В. М. Гусаров. – М. : Аудит, ЮНИТИ, 2011.
3 Мелкумов Я. С. Социально-экономическая статистика : учебно-методическое пособие / Мелкумов Я. С. – М. : ИМПЭ-ПАБЛИШ, 2010.
4 Елисеева И. И. Общая теория статистики : учебник для вузов / И. И. Елисеева, М. М. Юзбашев; под ред. И. И. Елисеевой. – М., 2010.
5 Сиденко А. В. Статистика : учебник / А. В. Сиденко, Г. Ю. Попов, В. М. Матвеева. – М. : Издательство «Дело и сервис», 2000.
6 Салин В. Н. Курс теории статистики для подготовки специалистов финансово-экономического профиля : учебник / В. Н. Салин, Э. Ю. Чурилова. – М. : Финансы и статистика, 2010.
7 Теория статистики : учебник для вузов / Р. А. Шмойлова и др.; под ред. Р. А. Шмойловой. – М.: Финансы и статистика, 2011.
Статистические группировки и классификации преследуют цели выделения качественно однородных совокупностей, изучения структуры совокупности, исследования существующих зависимостей. Каждой из этих целей соответствует особый вид группировки: типологическая, структурная, аналитическая (факторная).
Типологическая группировка решает задачу выявления и характеристики социально-экономических типов (частных подсовокупностей).
Структурная дает возможность описать составные части совокупности или строение типов, а также проанализировать структурные сдвиги.
Аналитическая (факторная) группировка позволяет оценивать связи между взаимодействующими признаками.
В зависимости от числа положенных в их основание признаков различают простые и многомерные группировки.
Группировка, выполненная по одному признаку, называется простой.
Многомерная группировка производится по двум и более признакам. Частным случаем многомерной группировки является комбинационная группировка, базирующаяся на двух и более признаках, взятых во взаимосвязи, в агрегатные комбинации.
Структурная группировка применяется для характеристики структуры совокупности сдвигов.
Структурной называется группировка, в которой происходит разделение выделенных с помощью технологической группировки типов явлений, однородных совокупностей на группы, характеризующие их структуру по какому-либо варьирующему признаку. Например, группировка населения по размеру среднедушевого дохода. Анализ структурных группировок, взятых за ряд периодов или моментов времени, показывает изменения структуры изучаемых явлений, то есть структурные сдвиги. В изменении структуры общественных явлений отражаются важнейшие закономерности их развития.
Показатель численности групп представлен либо частотой (количеством единиц в каждой группе), либо частотностью (удельным весом каждой группы).
Среди простых группировок особо выделяют ряды распределения.
Ряд распределения –это группировка, в которой для характеристики групп (упорядоченно расположенных по значению признака) применяется один показатель –численность группы. Другими словами, это ряд чисел, показывающий, как распределяются единицы некоторой совокупности по изучаемому признаку.
Ряды, построенные по атрибутивному признаку, называются атрибутивными рядами распределения.
Ряды распределения,
построенные по количественному признаку, называются вариационными рядами.
Примером атрибутивных рядов могут служить распределения населения по полу, занятости, национальности, профессии и т.д.
Примером вариационного ряда распределения могут служить распределения населения по возрасту, рабочих – по стажу работы, заработной плате и т.д.
Вариационные ряды распределения состоят из двух элементов вариантов и частот.
Вариантами называются числовые значения колличественного признака в ряду распределения, они могут быть положительными и отрицательными, абсолютными и относительными.
Частоты – это численности отдельных вариантов или каждой группы вариационного ряда. базисные Сумма всех частот называется объемом совокупности и определяет число элементов всей совокупности.
Вариационные ряды в зависимости от характера вариации подразделяются на дискретные и интервальные.
1.2 Абсолютные и относительные величины
Абсолютные величины – это результаты статистических наблюдений. В статистике в отличие от математики все абсолютные величины имеют размерность (единицу измерения), а также могут быть положительными и отрицательными.
Единицы измерения абсолютных величин отражают свойства единиц статистической совокупности и могут быть простыми, отражая 1 свойство (например, масса груза измеряется в тоннах) или сложными, отражая несколько взаимосвязанных свойств (например, тонно-километр или киловатт-час).
Единицы измерения абсолютных величин могут быть 3 видов:
1 Натуральные – применяются для исчисления величин с однородными свойствами (например, штуки, тонны, метры и т.д.). Их недостаток состоит в том, что они не позволяют суммировать разнородные величины.
2 Условно-натуральные –применяются к абсолютным величинам с однородными свойствами, но проявляющим их по-разному. Например, общая масса энергоносителей (дрова, торф, каменный уголь, нефтепродукты, природный газ) измеряется в т.у.т. – тонны условного топлива, поскольку каждый его вид имеет разную теплотворную способность, а за стандарт принято 29,3 мДж/кг. Аналогично общее количество школьных тетрадей измеряется в у.ш.т. – условные школьные тетради размером 12 листов. Аналогично продукция консервного производства измеряется в у.к.б. – условные консервные банки емкостью 1/3 литра. Аналогично продукция моющих средств приводится к условной жирности 40 %.
3 Стоимостные единицы измерения выражаются в рублях или в иной валюте, представляя собой меру стоимости абсолютной величины. Они позволяют суммировать даже разнородные величины, но их недостаток состоит в том, что при этом необходимо учитывать фактор инфляции, поэтому статистика стоимостные величины всегда пересчитывает в сопоставимых ценах.
1.3 Средние величины и показатели вариации
Средняя величина – это обобщающая характеристика совокупности однотипных явлений по изучаемому признаку.
Выбор средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин:
- арифметическая;
- гармоническая;
- квадратичная;
- геометрическая.
Каждая из них может быть простой и взвешенной. закономерности Перечисленные средние относятся к классу степенных средних и определяются формулой (при различных значениях m):
 , (2)
, (2)При m=-1 средняя гармоническая < http://chaliev.ru/statistics/srednie- velichiny-i-pokazateli-variatsyi.php>; =0 средняя геометрическая
Средняя арифметическая простая – это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:
где X – значения величин, для которых необходимо рассчитать среднее значение;
N – общее количество значений X (число единиц в изучаемой совокупности).
Средняя арифметическая взвешенная вычисляется когда варианты встречаются не одинаковое число раз.
2 Практическая часть
Постановка задачи.
Провести статистический анализ данных для переменных X и Y. Найти выборочные средние, дисперсии и среднеквадратические отклонения для X и Y по отдельности.
Найти ковариацию Cov (X, Y).
Найти коэффициент корреляции X и Y.
Найти по выборке уравнение линейной регрессии (Y как функцию X) по методу наименьших квадратов.
Найти по выборке уравнение параболической регрессии второго порядка (Y как функцию X) по методу наименьших квадратов.
Построить графики, изображающие данные выборки и найденные функции регрессии.
Проверить гипотезу о значимости выборочного коэффициента корреляции при заданном уровне значимости альфа =0,001.
Исходные данные.
Нам дана выборка (объемом n=20) зависимости числа Y от числа X.
Таблица 1 – Исходные данные
| Х | Y |
| 13,3 | 39,1 |
| 18 | 54,7 |
| 20,2 | 59,1 |
| 3,4 | 10,8 |
| 16,5 | 50,9 |
| 5,4 | 24,1 |
| 23,8 | 62,5 |
| 0,5 | 4,6 |
| 18,4 | 56,4 |
| 10,3 | 40,9 |
| 7,6 | 26,1 |
| 0,3 | -0,1 |
| 17,8 | 48,1 |
| 0,4 | 3,9 |
| 15,1 | 52,2 |
| 14,6 | 49 |
| 0,8 | 0 |
| 5,4 | 25,5 |
| 24,6 | 59,7 |
| 8 | 26,5 |
Статистический анализ данных для переменных X и Y.
Найдем выборочные средние для X и Y по формуле (1):
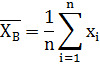 , (4)
, (4)Найдем выборочные дисперсии для X и Y по формуле (2) и (3):
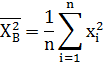 , (7)
, (7)Найдем выборочные среднеквадратические отклонения для X и Y по формуле (4):
Ковариация Cov (X, Y).
Найдем выборочную ковариацию для переменных X и Y по формуле (18):
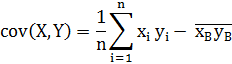 , (18)
, (18)Коэффициент корреляции X и Y.
Найдем выборочный коэффициент корреляции для переменных X и Y по формуле (20:
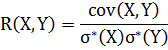 , (20)
, (20)Уравнение линейной регрессии.
Найдем коэффициенты a и b для уравнения линейной регрессии.
Для нахождения коэффициентов a и b методом наименьших квадратов были посчитаны следующие необходимые параметры:
 , (22)
, (22) , (23)
, (23)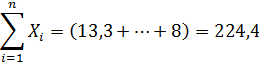 , (24)
, (24)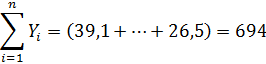 , (25)
, (25)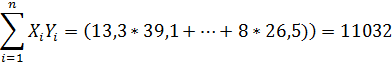 , (26)
, (26)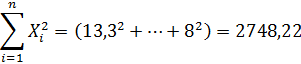 , (27)
, (27)Тогда коэффициенты
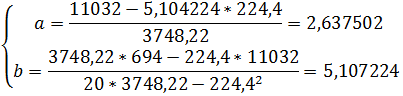 , (28)
, (28)Таким образом, получаем уравнение линейной регрессии:

Рисунок 1 – Линейная регрессия
Гипотеза о значимости выборочного коэффициента корреляции.
Проверим гипотезу о значимости выборочного коэффициента корреляции, для этого вычислим
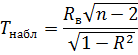 , (30)
, (30)Получаем:
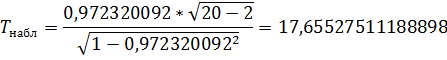 , (32)
, (32)Поскольку
Заключение
В данной курсовой работе были вычислены основные числовые характеристики выборок по X и Y.
По выборке проведено исследование корреляционной зависимости по выборке. Найдены ковариация и коэффициент корреляции. В результате проведенной работы были закреплены теоретические знания и приобретены практические навыки работы со статистиками, умение находить точечные и интервальные оценки математического ожидания и дисперсии.
Был изучен метод регрессионного анализа, при помощи которого удаётся провести зависимость прожиточного минимума (Y) от заработной платы (X).
Список использованных источников
1 Статистика : учебное пособие / А. В. Багат и др.; под ред. В. М. Симчеры. – М. : Финансы и статистика, 2011.
2 Гусаров В. М. Теория статистики : учебное пособие для вузов / В. М. Гусаров. – М. : Аудит, ЮНИТИ, 2011.
3 Мелкумов Я. С. Социально-экономическая статистика : учебно-методическое пособие / Мелкумов Я. С. – М. : ИМПЭ-ПАБЛИШ, 2010.
4 Елисеева И. И. Общая теория статистики : учебник для вузов / И. И. Елисеева, М. М. Юзбашев; под ред. И. И. Елисеевой. – М., 2010.
5 Сиденко А. В. Статистика : учебник / А. В. Сиденко, Г. Ю. Попов, В. М. Матвеева. – М. : Издательство «Дело и сервис», 2000.
6 Салин В. Н. Курс теории статистики для подготовки специалистов финансово-экономического профиля : учебник / В. Н. Салин, Э. Ю. Чурилова. – М. : Финансы и статистика, 2010.
7 Теория статистики : учебник для вузов / Р. А. Шмойлова и др.; под ред. Р. А. Шмойловой. – М.: Финансы и статистика, 2011.

