О НАЗНАЧЕНИИ ПОЛЮСОВ В МНОГОВХОДНЫХ УПРАВЛЯЕМЫХ ЛИНЕЙНЫХ СИСТЕМАХ
Аннотация - Показано, что управляемость системы с разомкнутым контуром эквивалентна возможности присвоения произвольного набора полюсов матрице передачи системы с замкнутым контуром, образованной с помощью подходящей линейной обратной связи состояния. В качестве приложения этого результата показано, что система с разомкнутым контуром может быть стабилизирована линейной обратной связью тогда и только тогда, когда неустойчивые моды ее системной матрицы являются управляемыми. Показано, что двойственность этого критерия эквивалентна существованию наблюдателя типа Люнбергера для идентификации асимптотического состояния.

Ключевые слова: управляемость системы, обратная связь, размещения полюсов, разомкнутой контур, критерия эквивалента, линейная система.
ВВЕДЕНИЕ

Рассмотрим систему

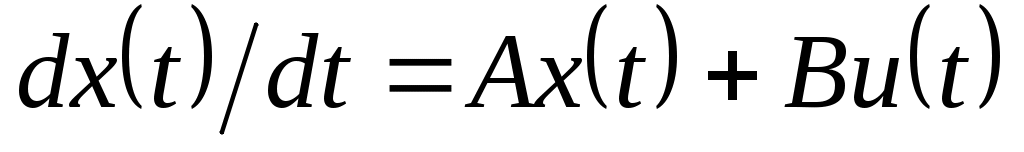
. (1)

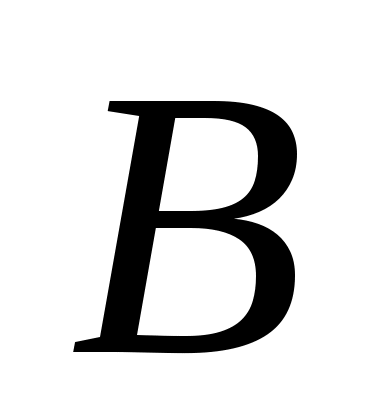
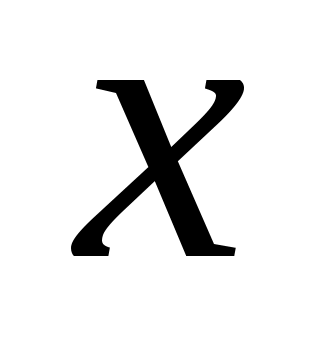
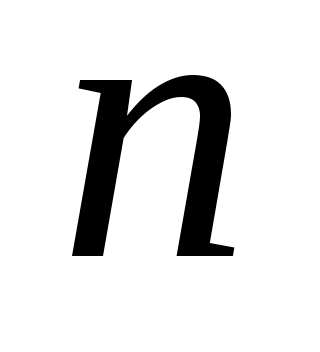
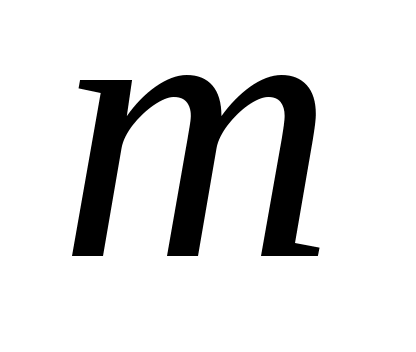
Здесь и далее все векторы и матрицы имеют вещественные элементы, а все матрицы являются константами. В (l) и - матрицы размерности и соответственно; - это вектор , обозначающий состояние, а - вектор , который, как обычно, обозначает внешний вход. Рассмотрим замкнутую систему, определяемую



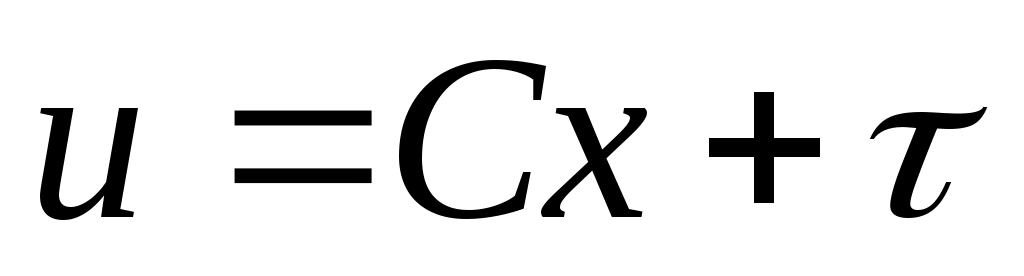
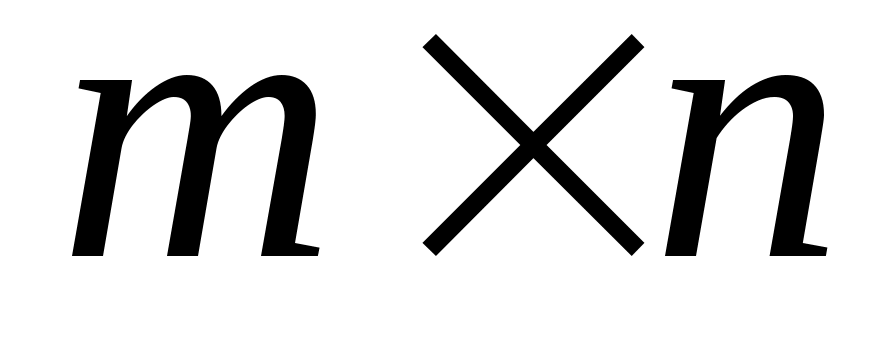
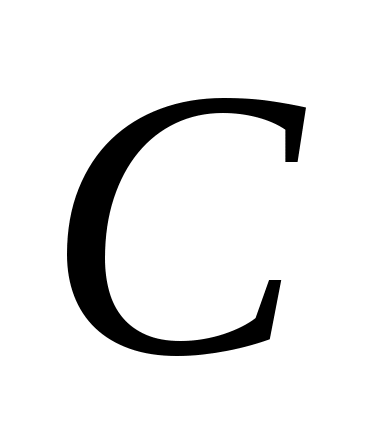
для некоторой матрицы и нового внешнего входа

---

.

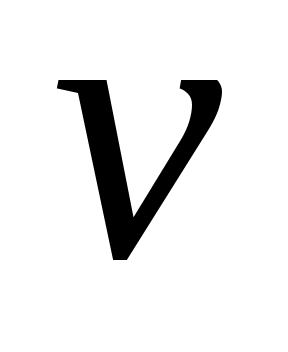
Тогда (1) становится

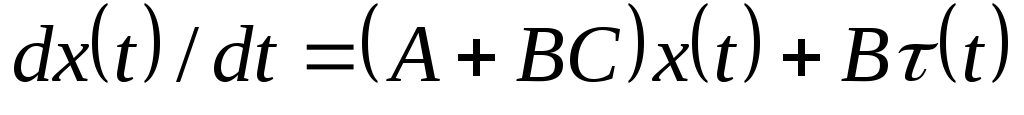
. (2)

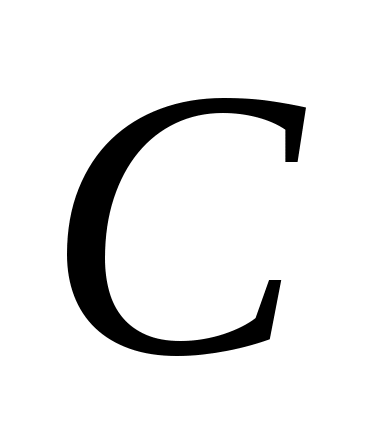
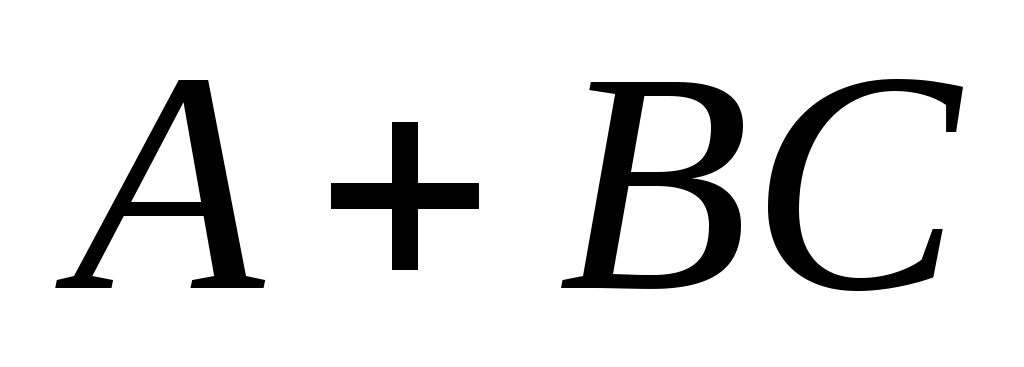
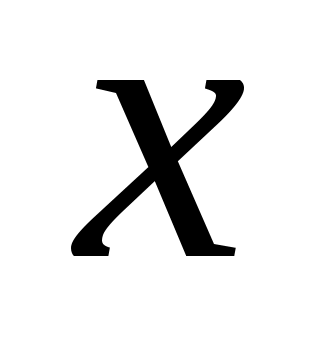
В приложениях часто желательно выбирать так, чтобы матрица имела особые свойства, например, стабильность. Интуитивно понятно, что возможность такого выбора зависит от управляемости, в соответствующем смысле, состояния относительно . Эта статья посвящена свойству «размещение полюсов», которое, как показано, эквивалентно управляемости (1) в обычном смысле. Чтобы быть точным, учтите следующее



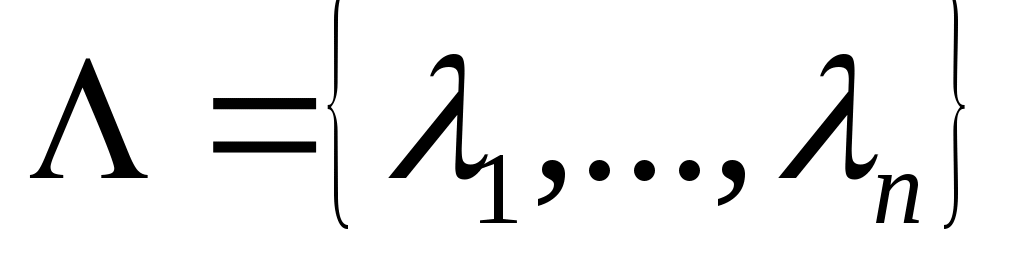
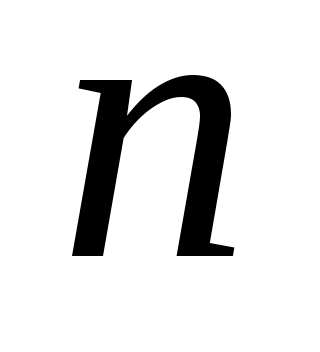
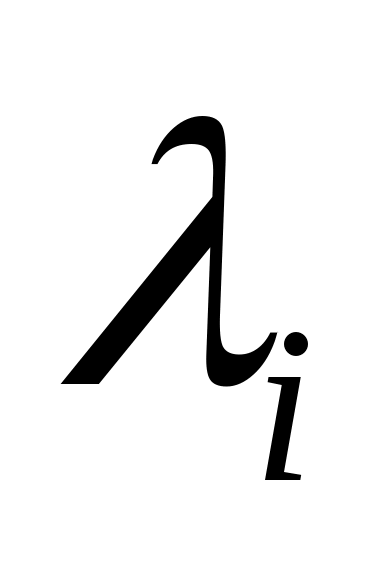
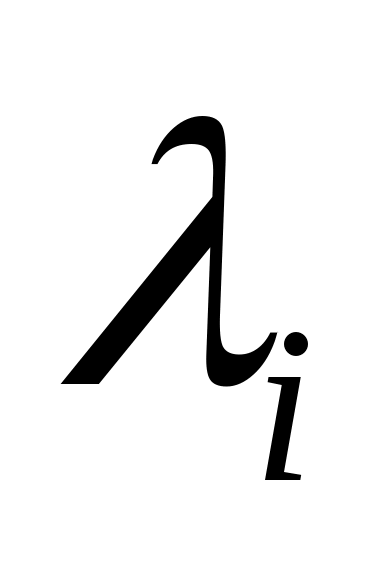
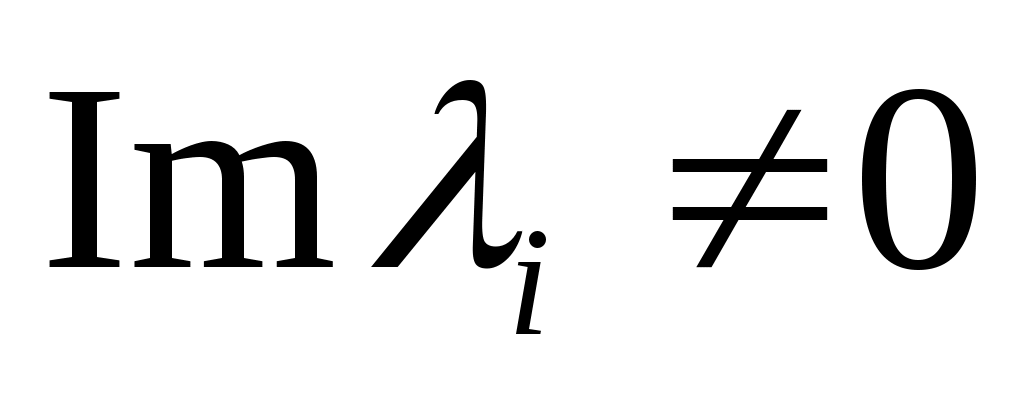
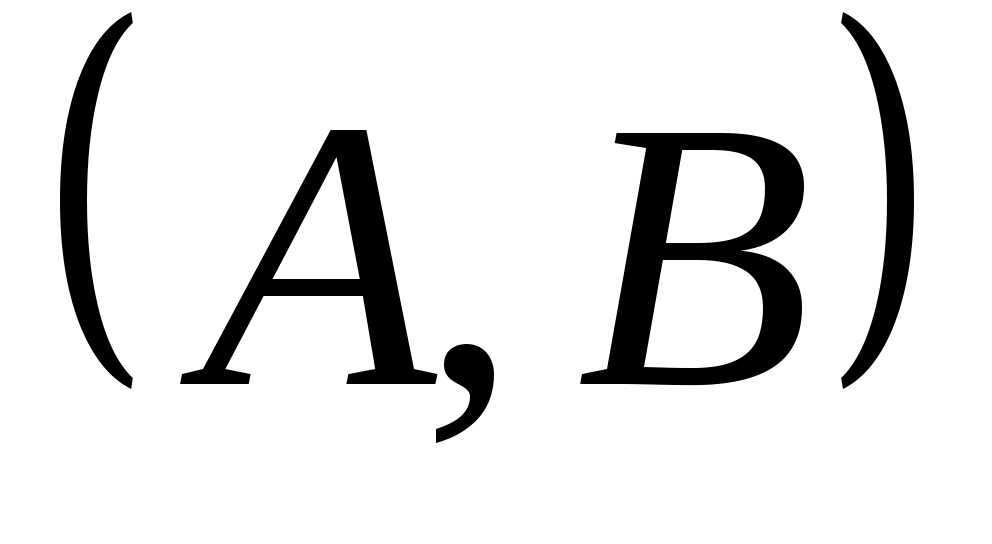
быть произвольным набором из комплексных чисел , так что любой с появляется в в сопряженной паре. Также напомним, что пара (полностью) управляема тогда и только тогда, когда матрица



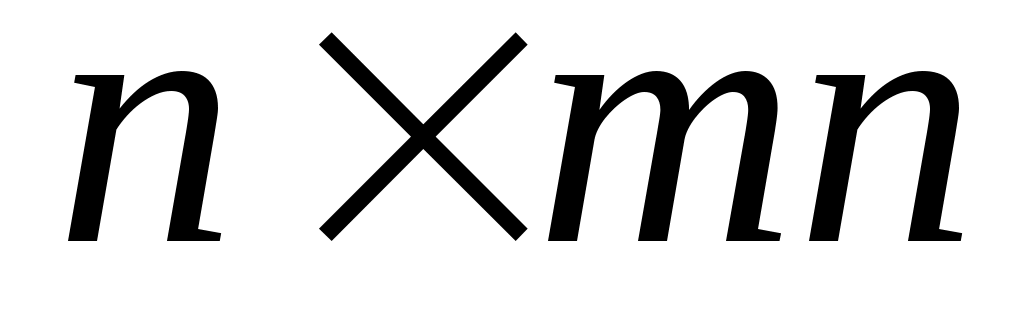
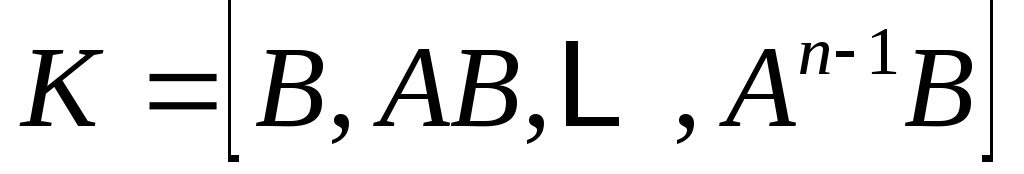
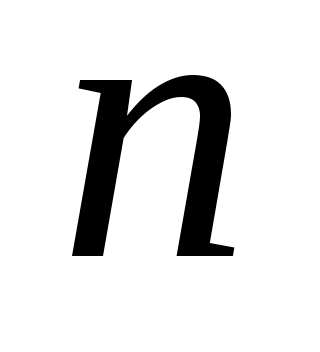
имеет полный ранг . Тогда основной результат, который нужно доказать, состоит в следующем.

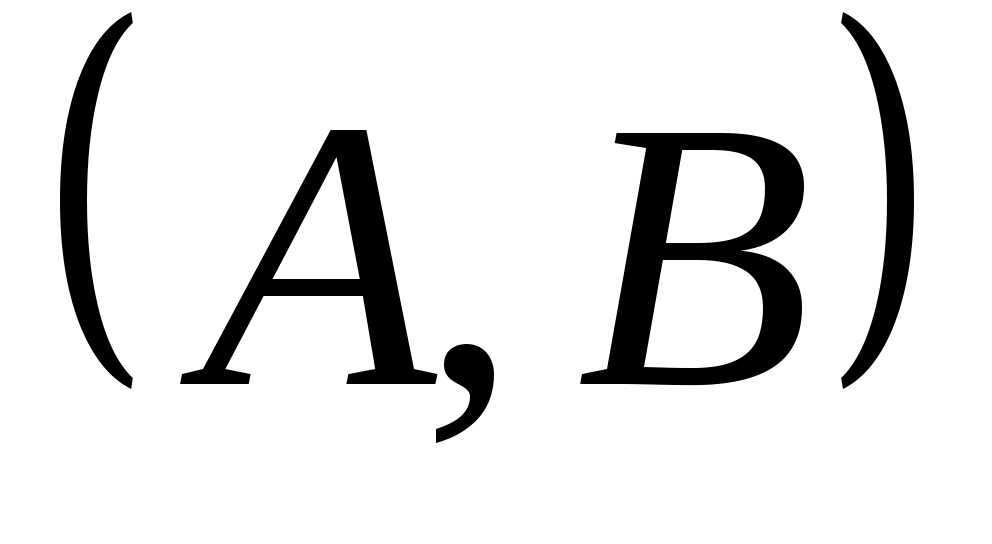
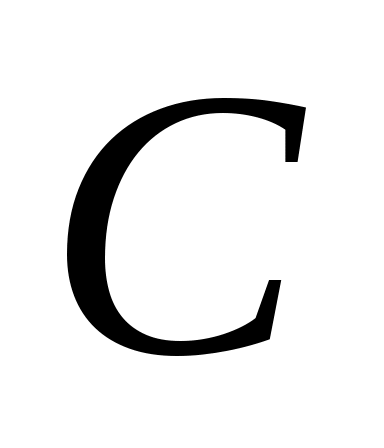
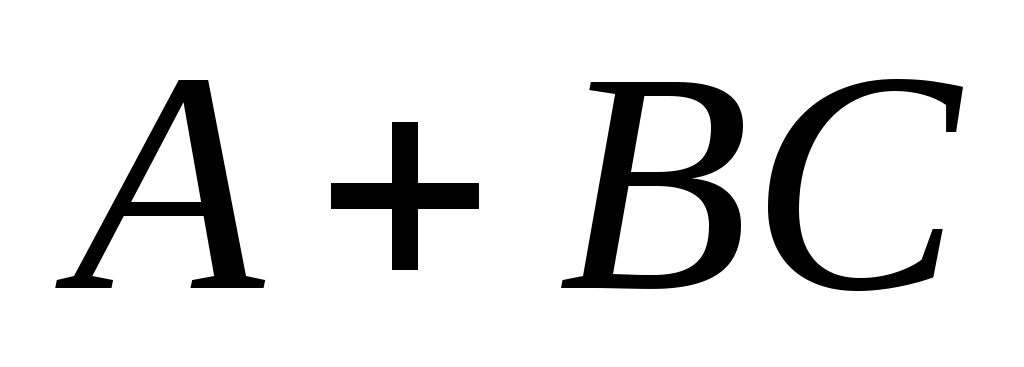
Теорема: Пара является управляемой тогда и только тогда, когда для каждого выбора множества существует матрица , такая, что имеет

---

для своего набора собственных значений.

Другими словами, управляемость эквивалентна тому свойству, что матрица передачи с обратной связью



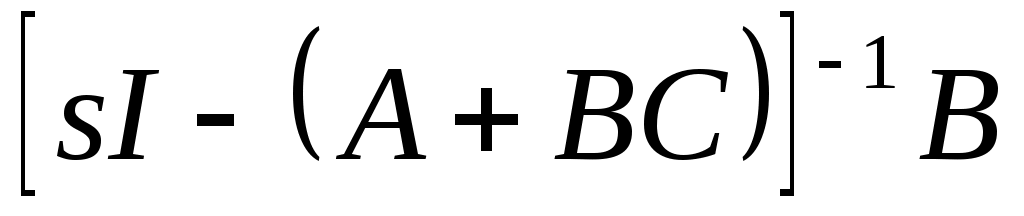
может быть назначен произвольный набор полюсов путем подходящего выбора матрицы «усиления» обратной связи .

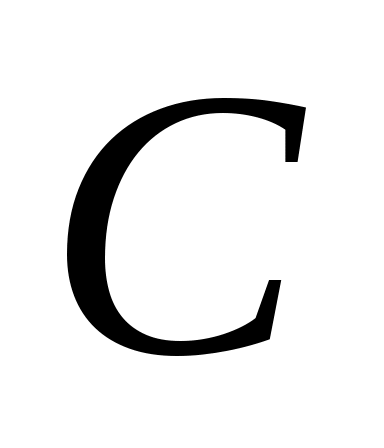
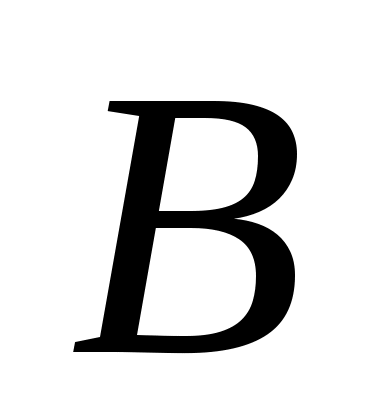
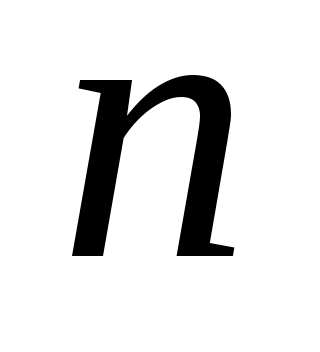
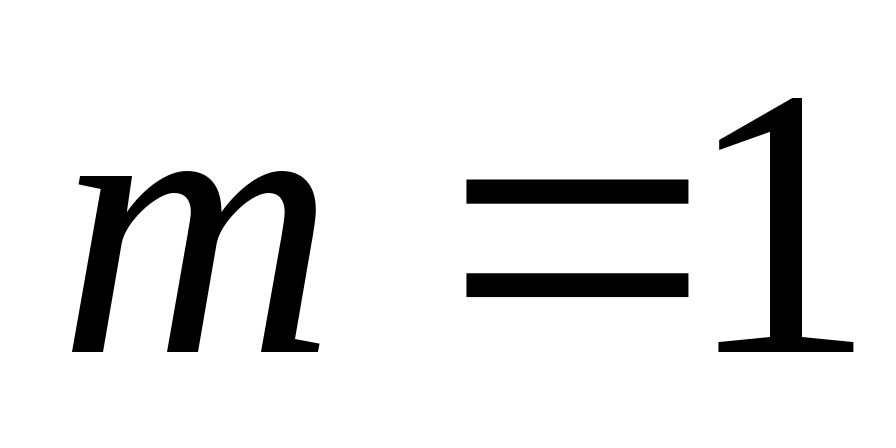
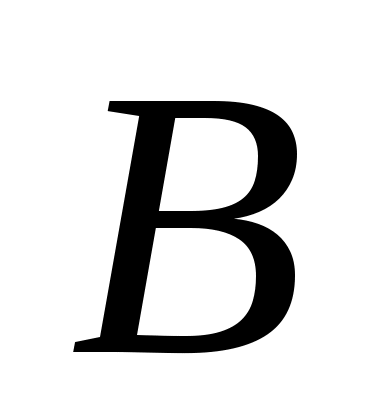
Если является -вектором ( ), указанный результат хорошо известен и становится очевидным после изменения базиса, которое преобразует к сопутствующей (рациональной канонической) форме и к форме



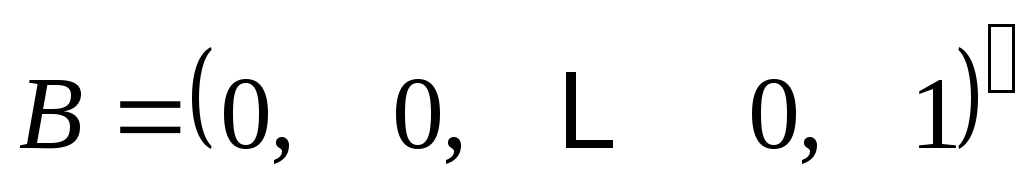
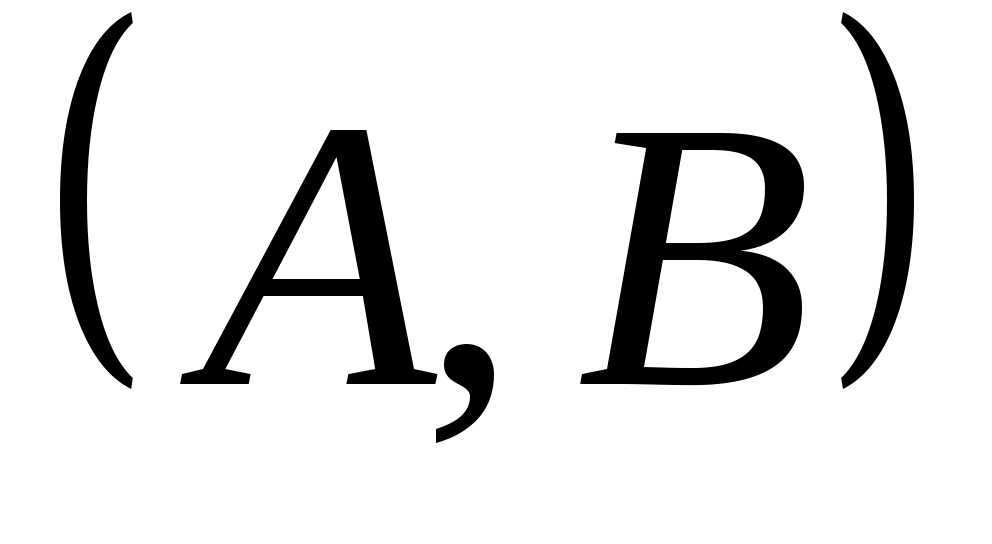
где штрих обозначает транспонирование. Такой выбор базиса всегда возможен, если управляемо [l].

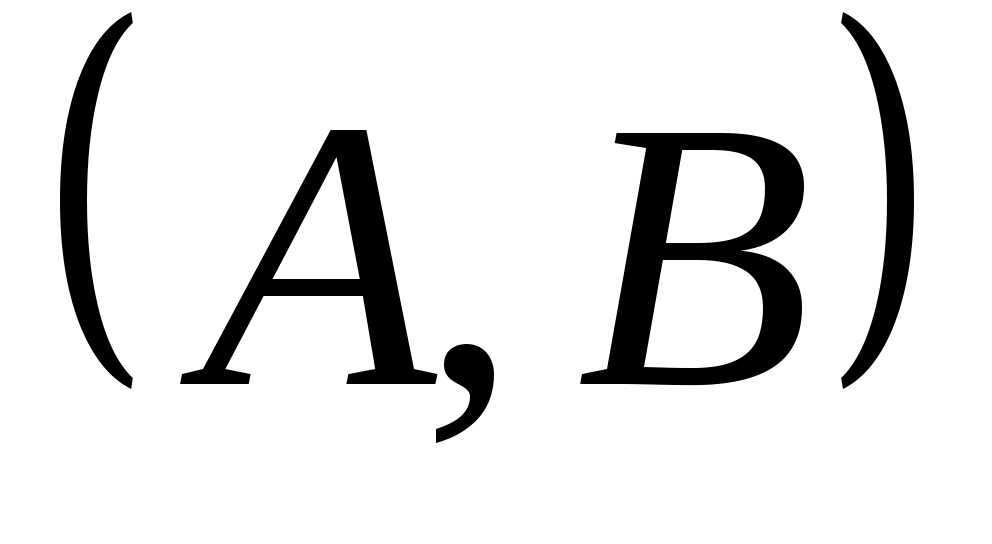
Чтобы доказать результат в общем случае, пара сначала преобразуется в каноническую форму, в которой система с несколькими входами представлена в виде треугольного массива, из которых диагональные блоки являются системами только что описанного типа. Это преобразование было использовано Лангенхопом [2], а затем в двойном контексте Бассом и Гурой [6] и Люнбергером [7]. 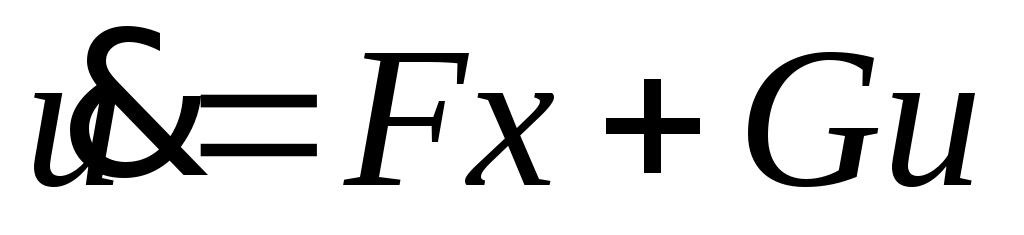Лангенхоп доказал теорему, аналогичную изложенной выше, в случае, когда и где элементы матриц параметров могут быть произвольными комплексными числами. Существующее ограничение на матрицы с вещественными элементами, очевидно, препятствует немедленному результату Лангенхопа; но эта трудность преодолевается путем использования предварительных результатов.

---

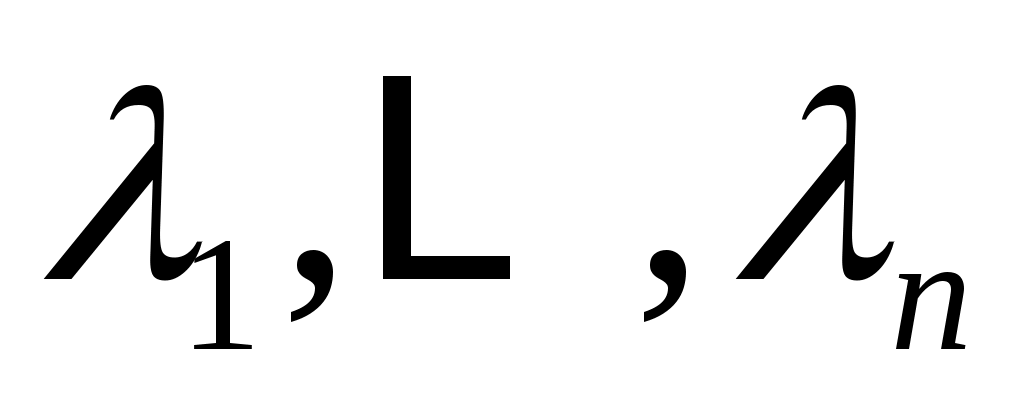
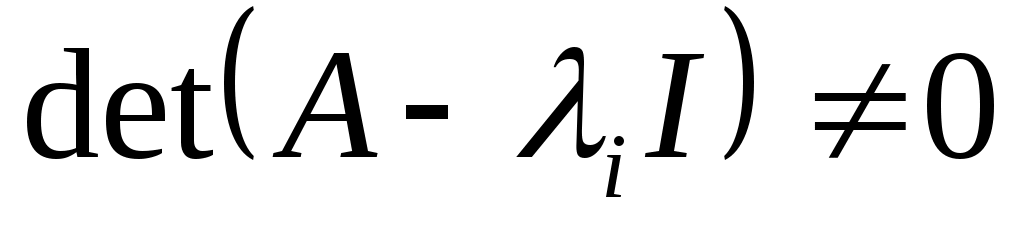
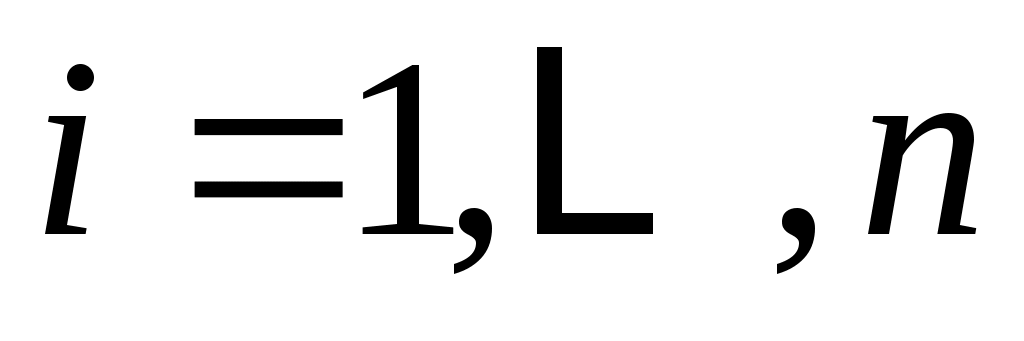
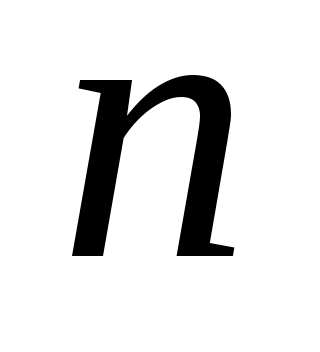
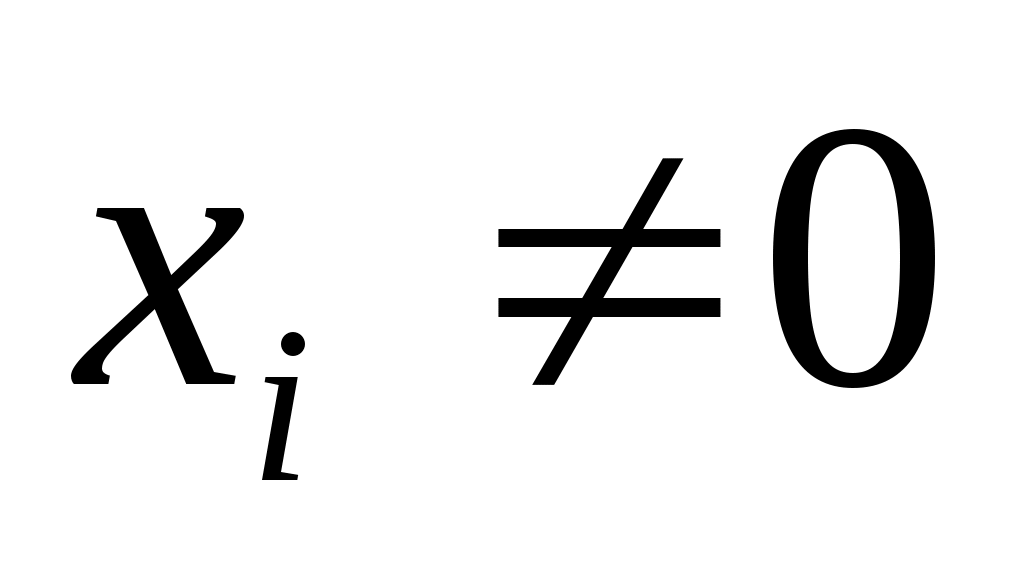
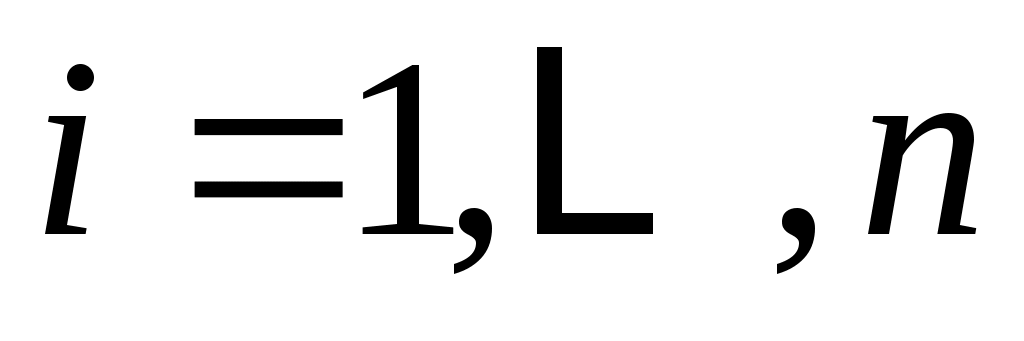
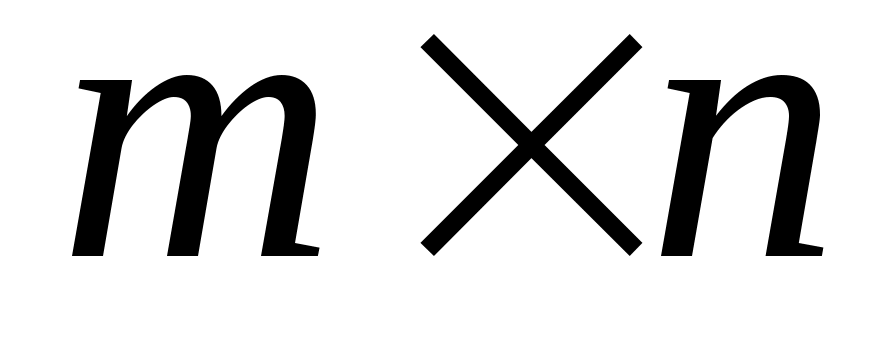
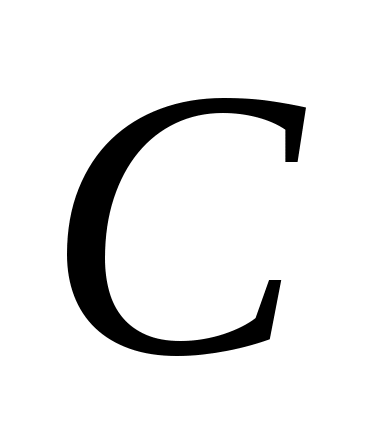
Доказательство теоремы. Аргумент Лангенхопа [2] применяется без изменений. Фактически, пусть - это любые различные действительные числа, такие что , . По предположению, существует векторов , и -матрица , такая тот

,

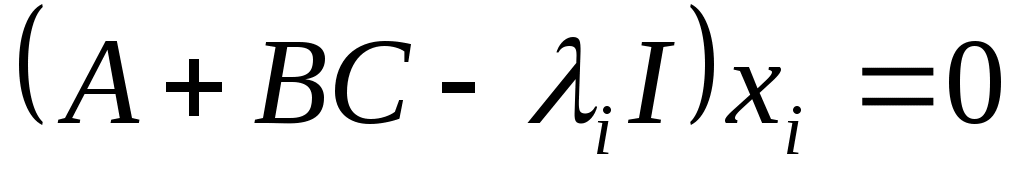
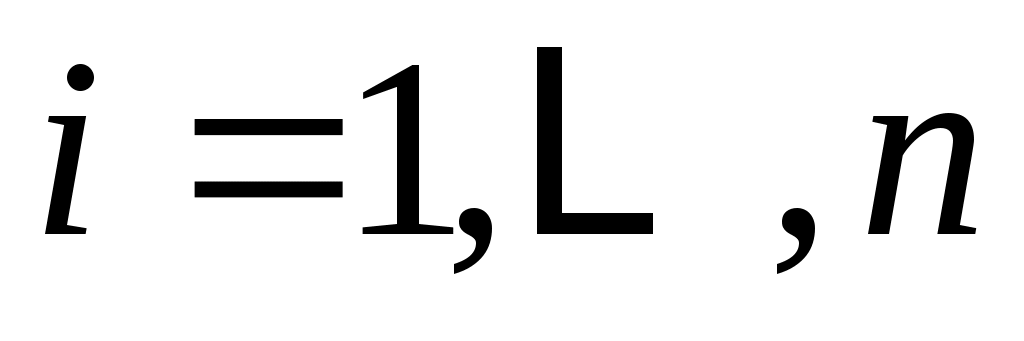
или

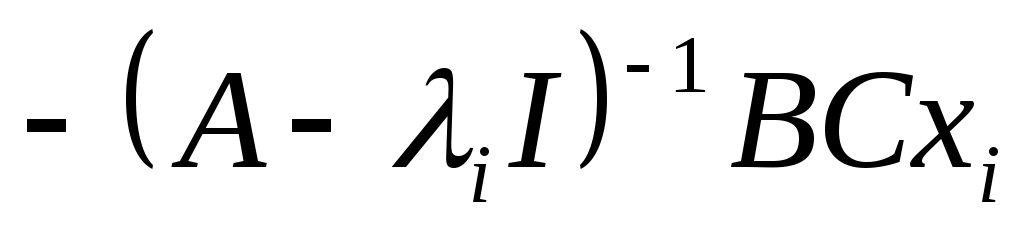
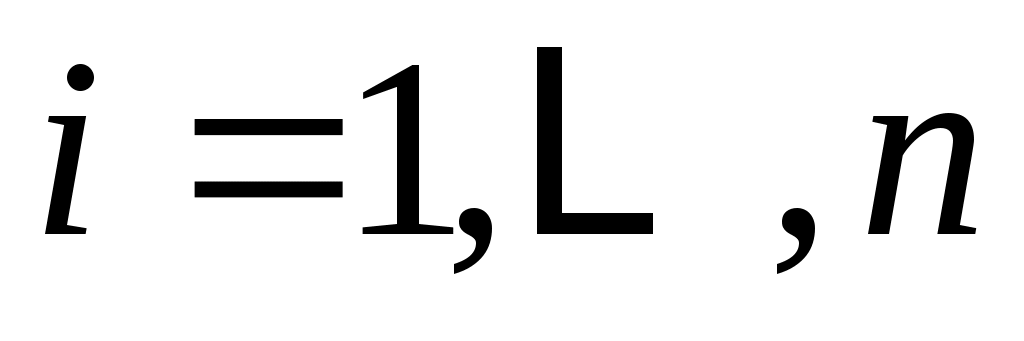
, . (3)

поскольку



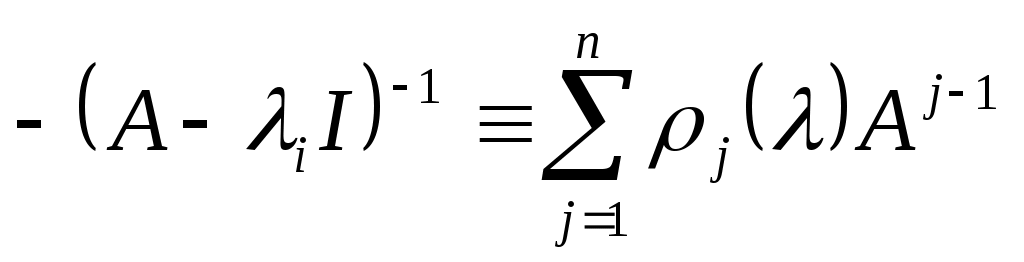
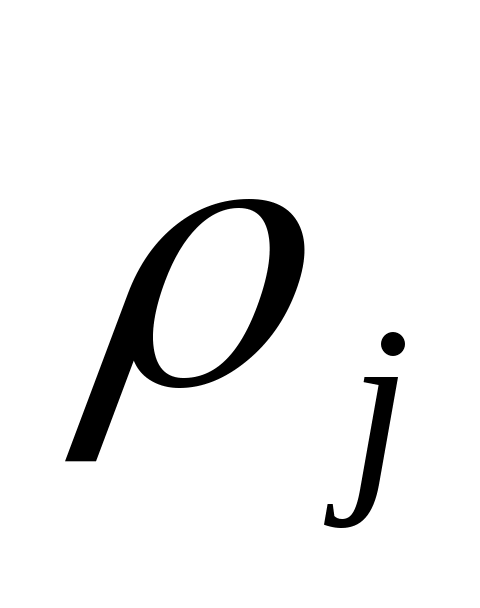
для подходящих рациональных функций из (3) следует

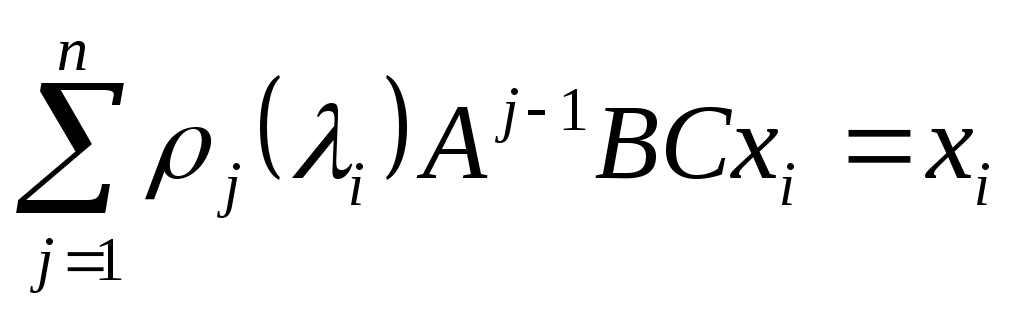
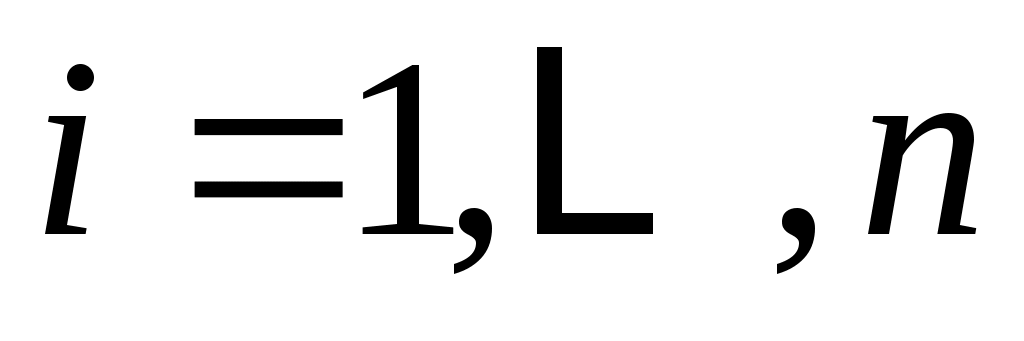
, . (4)

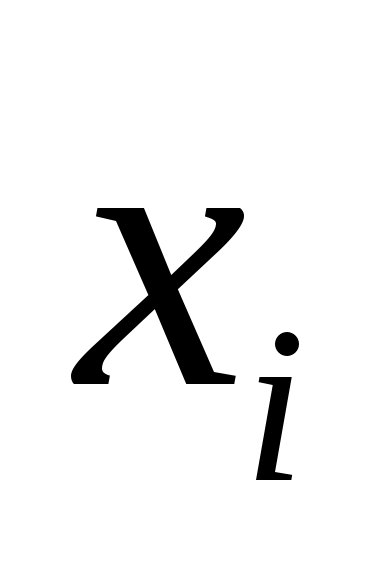
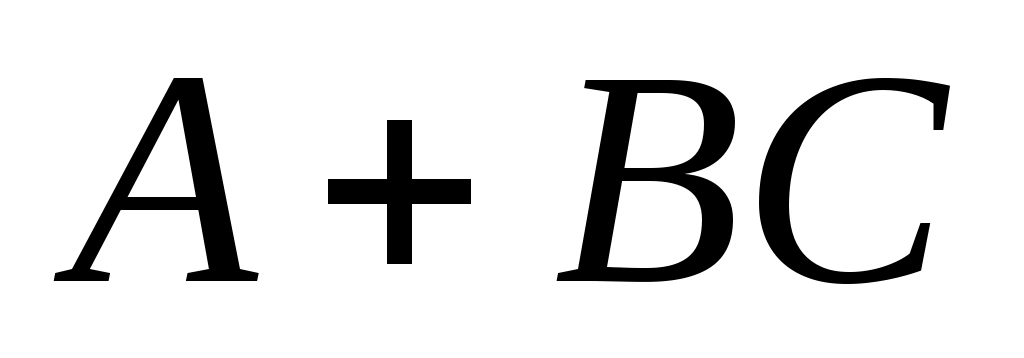
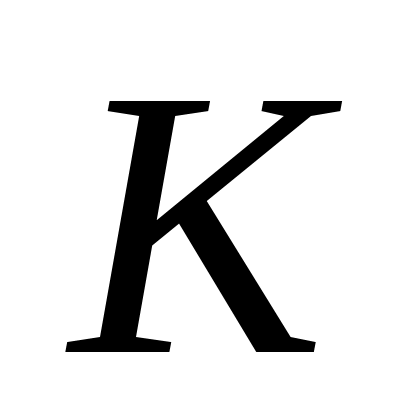
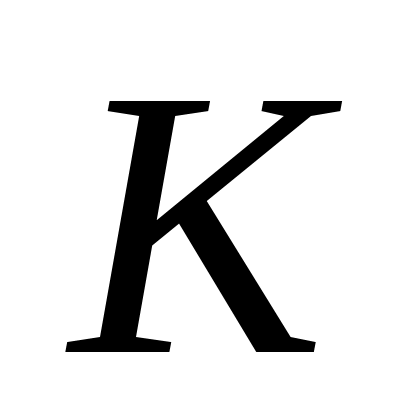
Поскольку различны, собственные векторы матрицы линейно независимы. Таким образом, (4) утверждает, что область является целым пространством, то есть имеет ранг .

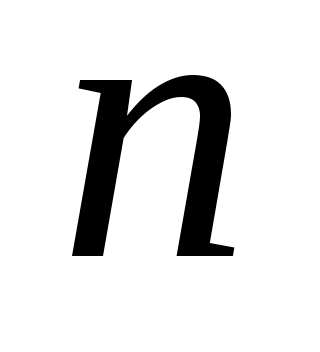
Доказательство необходимости опирается на теорию циклических подпространств [3]. Для полноты предварительные результаты собраны ниже.

---

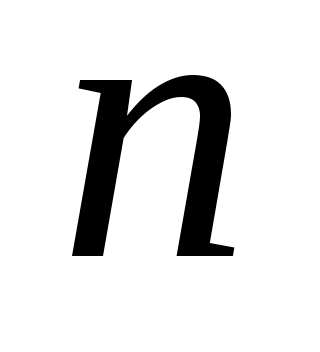
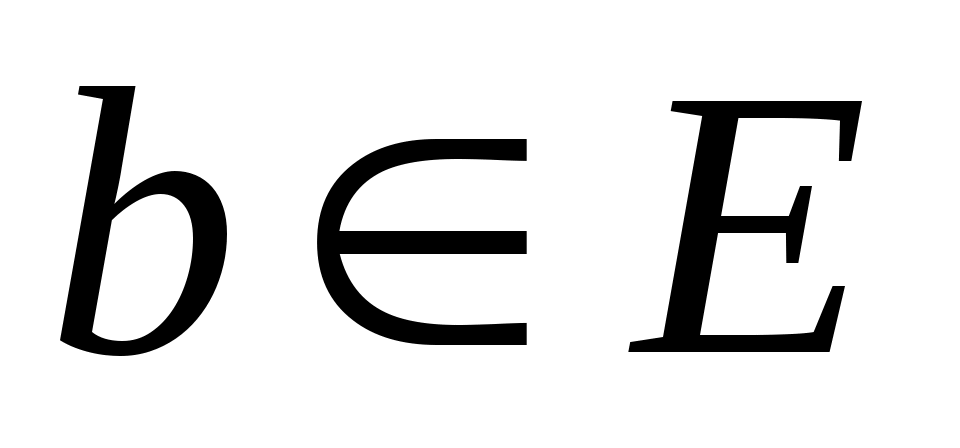
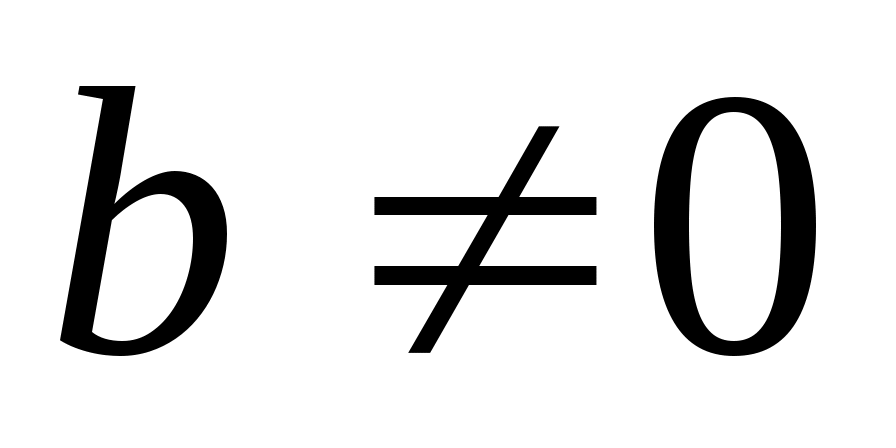
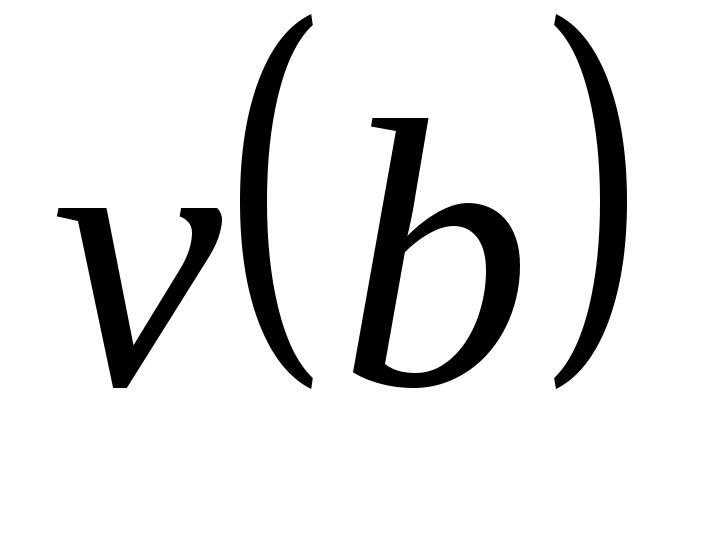
1) Предварительные результаты. Обозначим через координату и пусть матрица будет фиксированной. Если и , пусть будет наибольшим целым числом, таким, что векторы



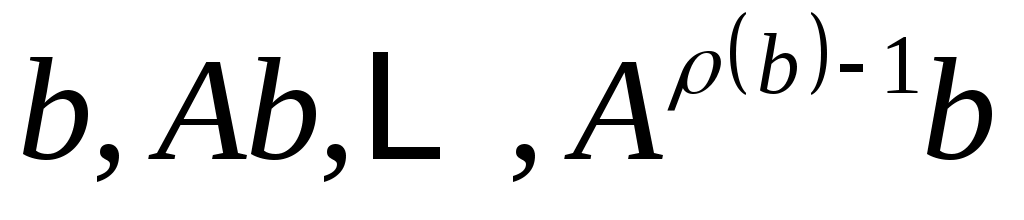
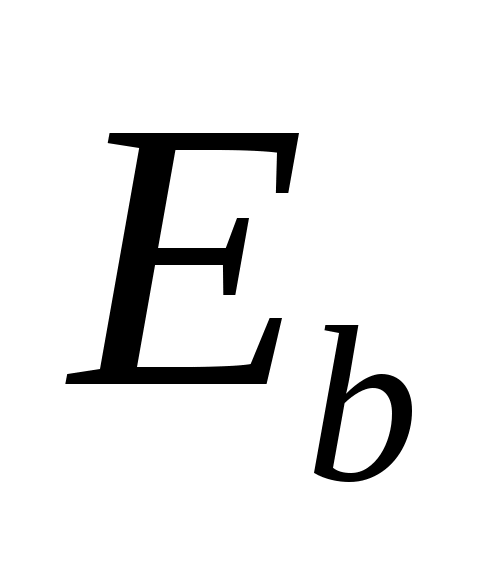
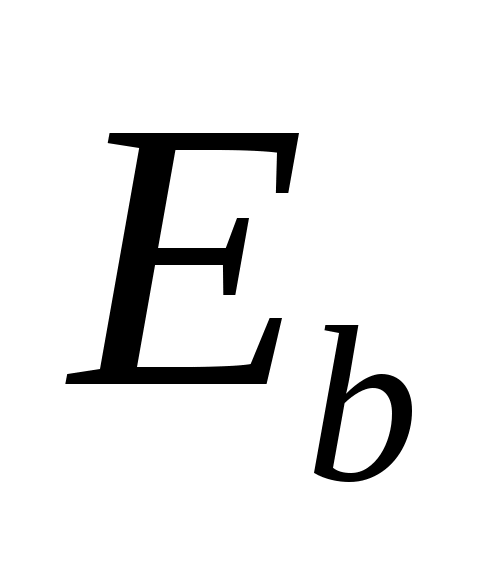
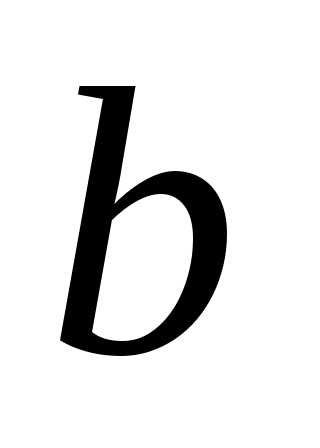
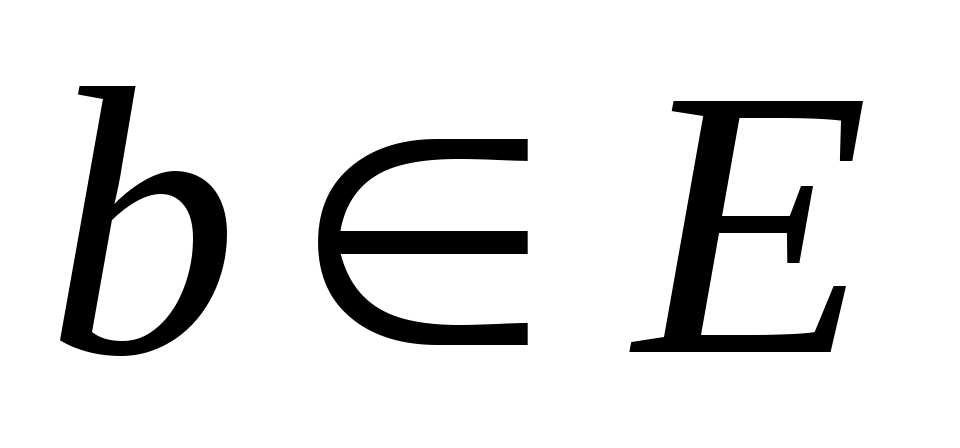
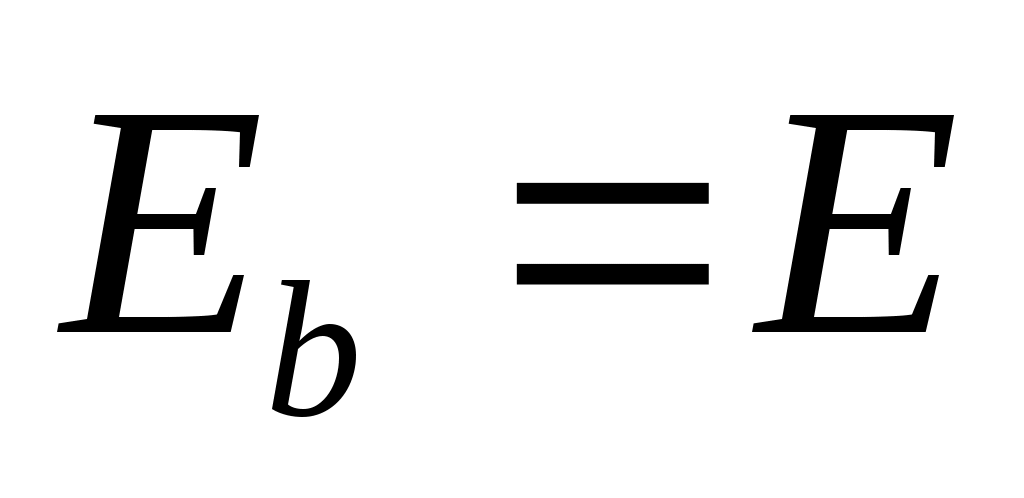
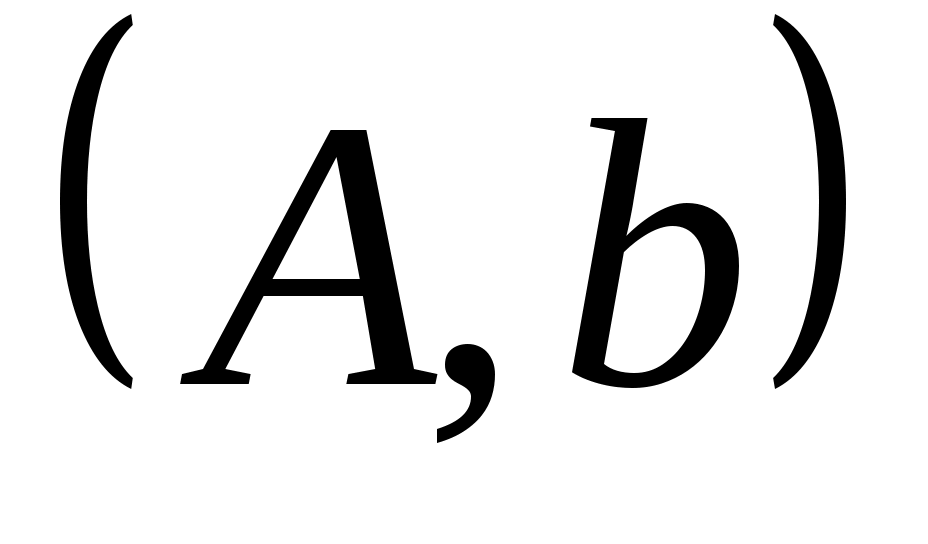
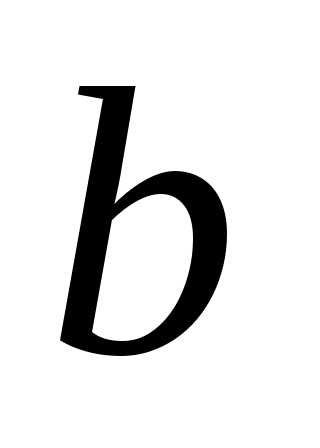
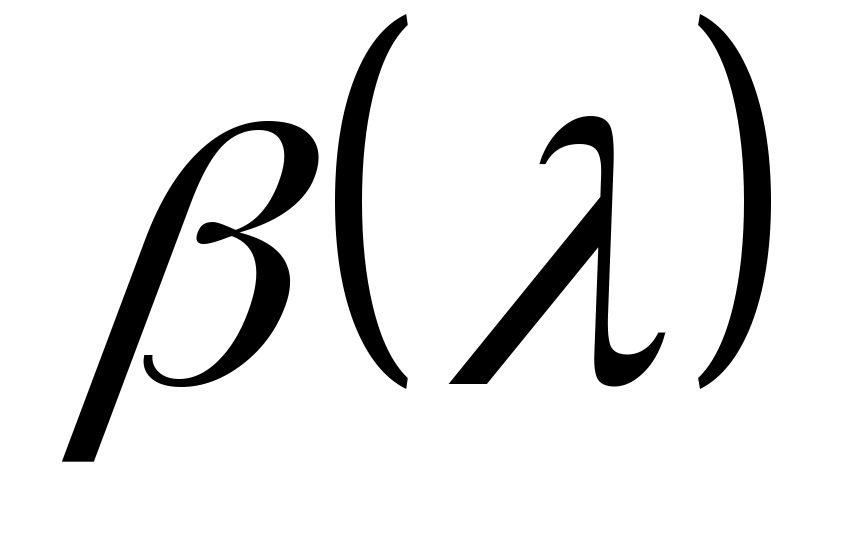
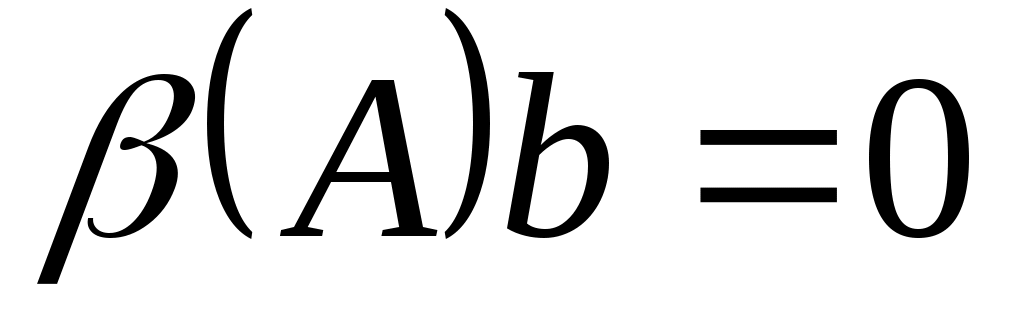
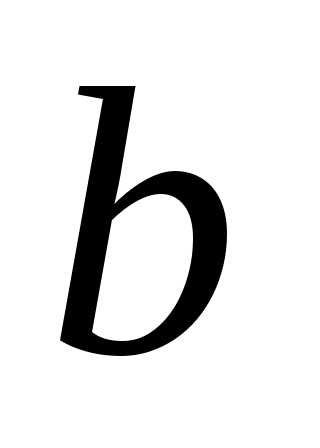
линейно независимы, и пусть обозначает их размах. - циклическое подпространство, порожденное . является циклическим, если существует , такой что , то есть такой, что является управляемым. Минимальный полином для -это (единственный) нормированный многочлен самой низкой степени, такой что . Таким образом, генерирует тогда, когда минимальный полином для

---

Смотрите также файлы

• Жаанды зыреттіліктер курсыны за мерзімді жоспары 8сынып ( барлыгы 18 са, аптасына 0,5 са).docx

• Отработка приемов с ручными пожарными лестницами.docx

• Oсобенности социальной стратификации традиционного казахского общества.docx

• Выполнение лабораторной работы по дисциплине информационные технологии в юридической деятельности.docx

• 6 апта Білім, ылым, техника жне технологиялар.docx