Файл: О назначении полюсов в многовходных управляемых линейных системах.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.03.2024
Просмотров: 24
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. То есть пусть  будет матрицей с векторами столбцов
будет матрицей с векторами столбцов 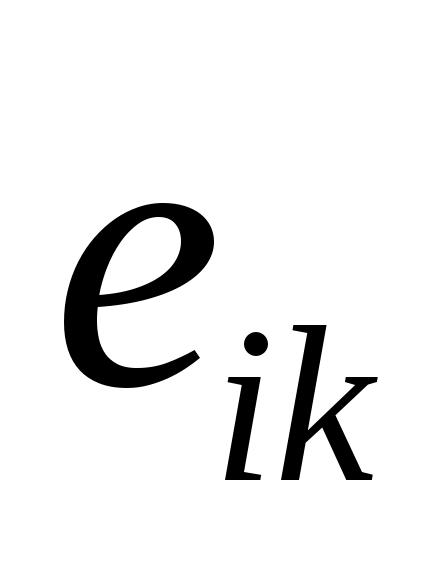 в только что написанном порядке, и пусть
в только что написанном порядке, и пусть 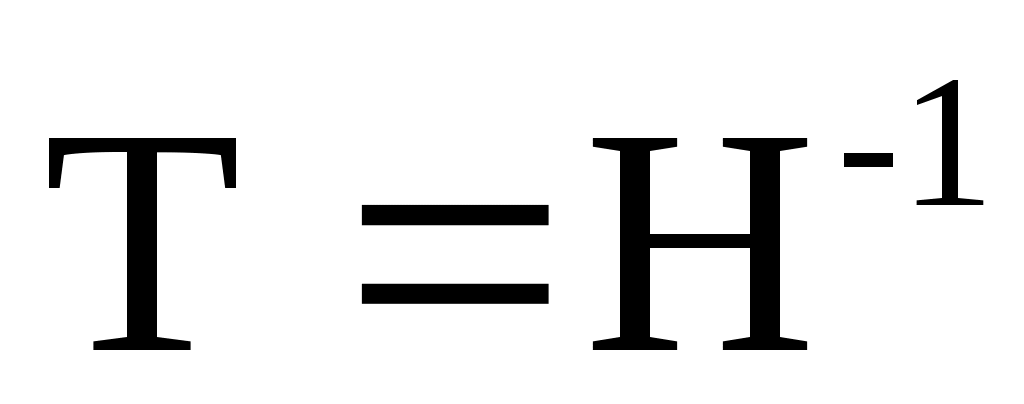 . Тогда
. Тогда 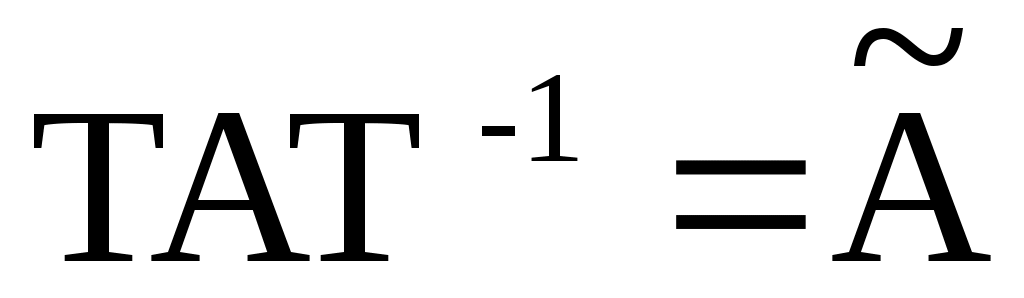 имеет блочную форму
имеет блочную форму
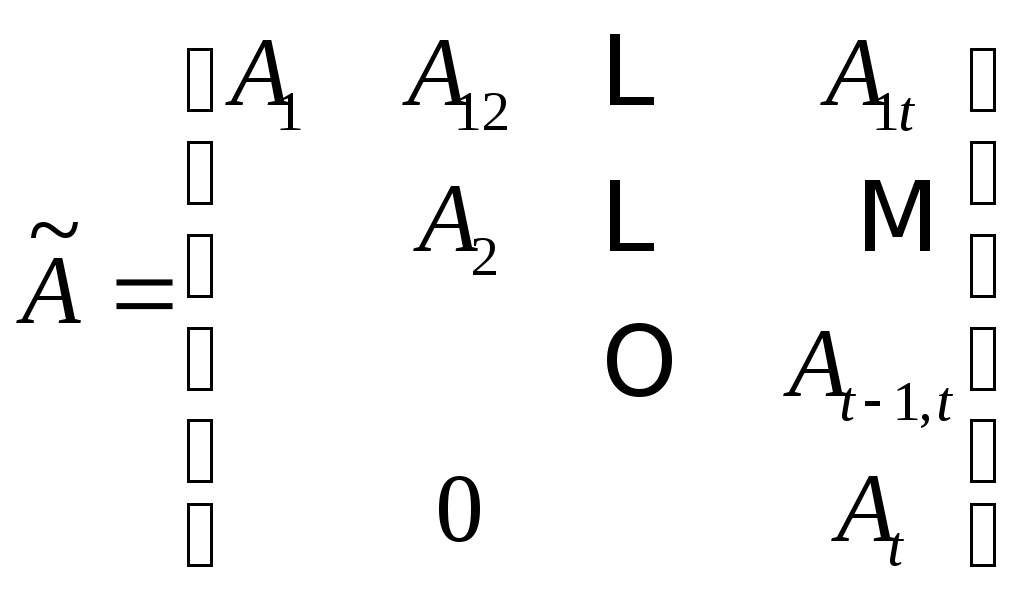 . (10)
. (10)
В (10) матрицы встречающиеся на диагонали
встречающиеся на диагонали 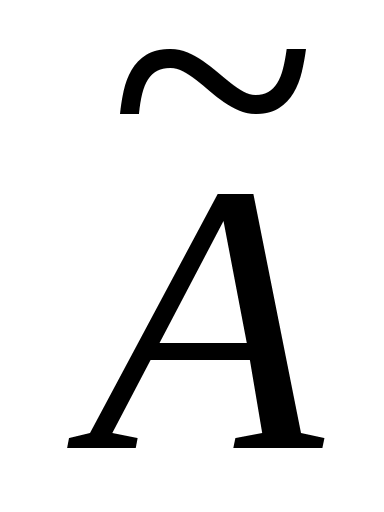 являются сопутствующими матрицами
являются сопутствующими матрицами 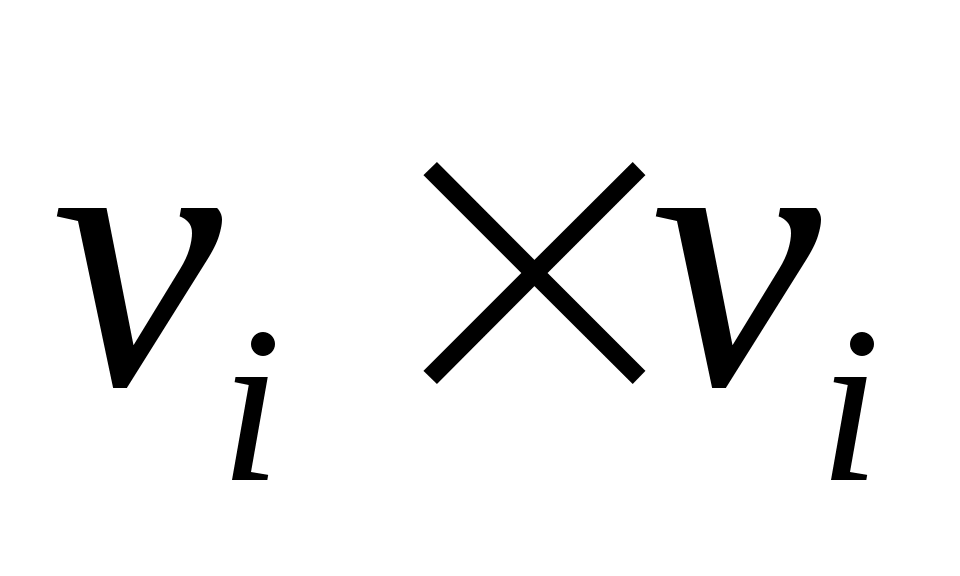 .
.
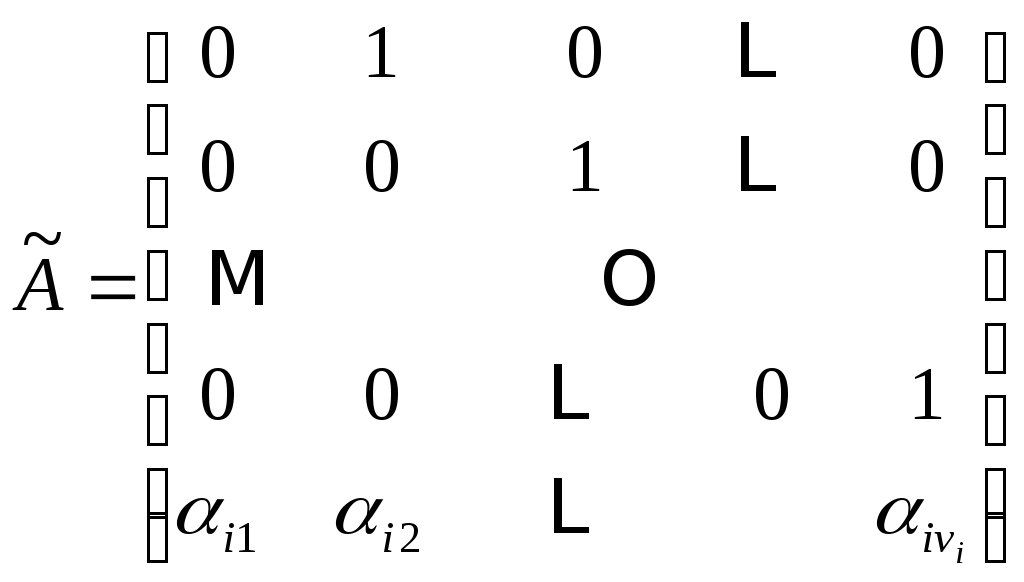 ,
, 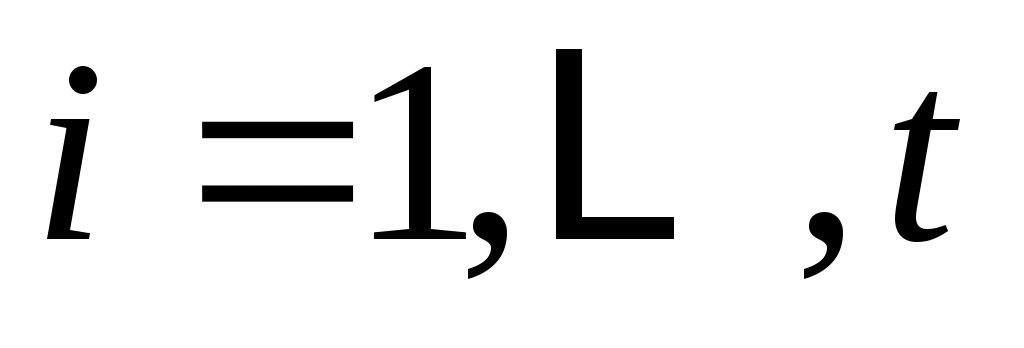 (11)
(11)
и матрицы имеют размерность
имеют размерность 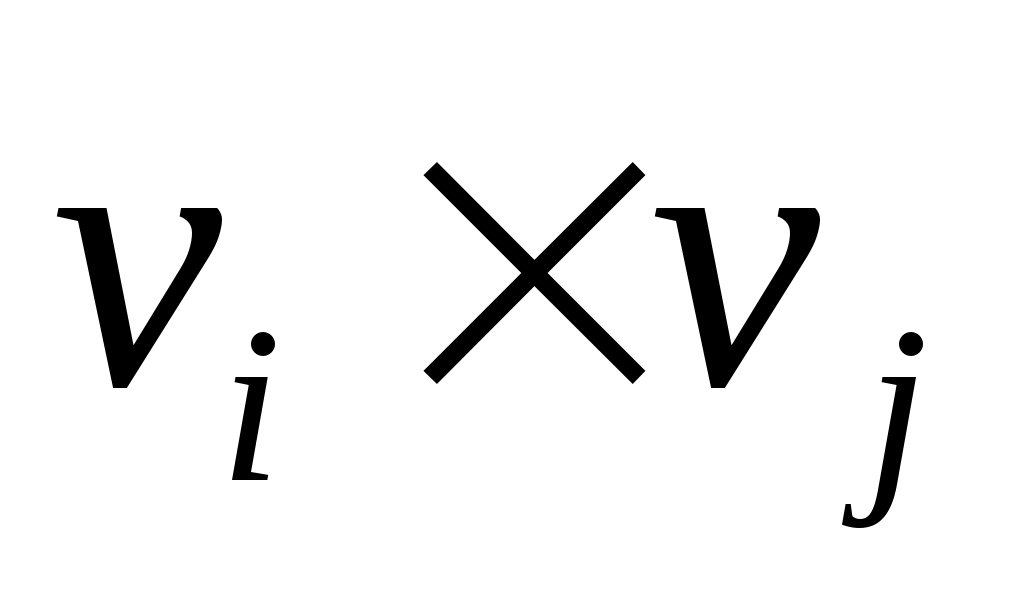 .
.
Наконец,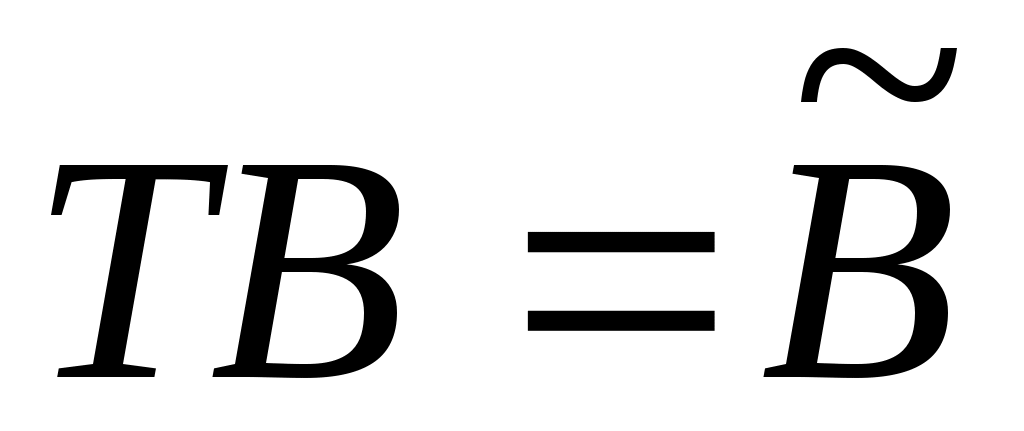 , где
, где
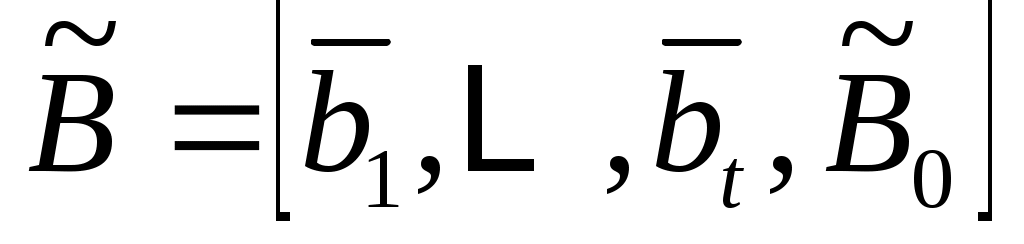 (12a)
(12a)
здесь
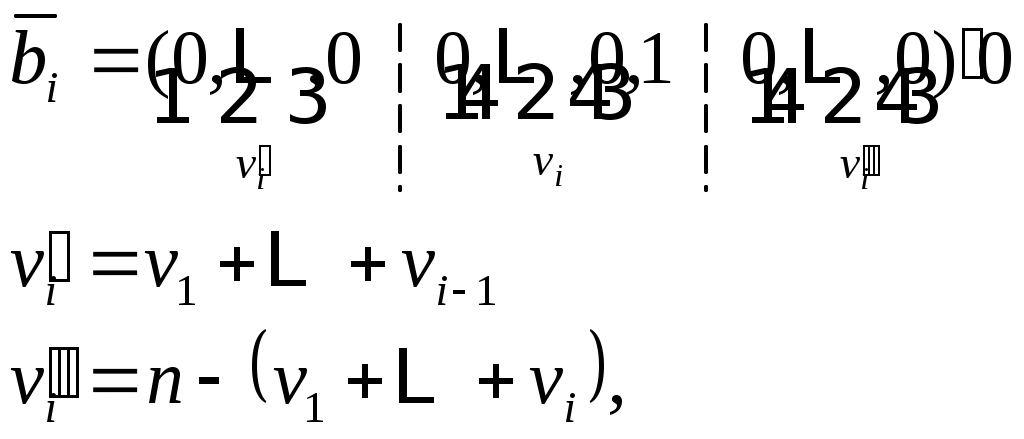 (12b)
(12b)
и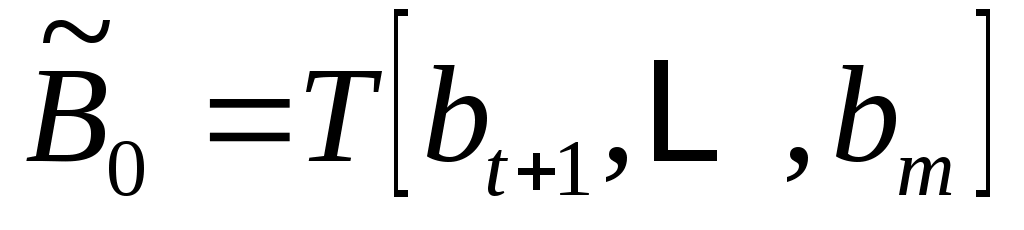 - матрица
- матрица 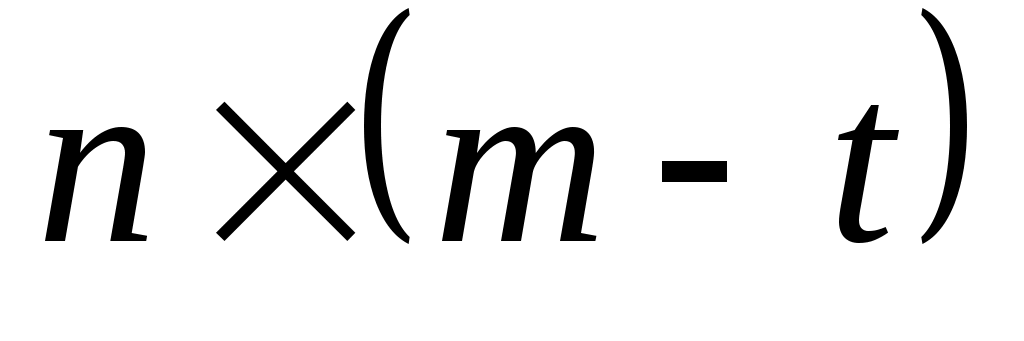 , которая не появляется, если
, которая не появляется, если 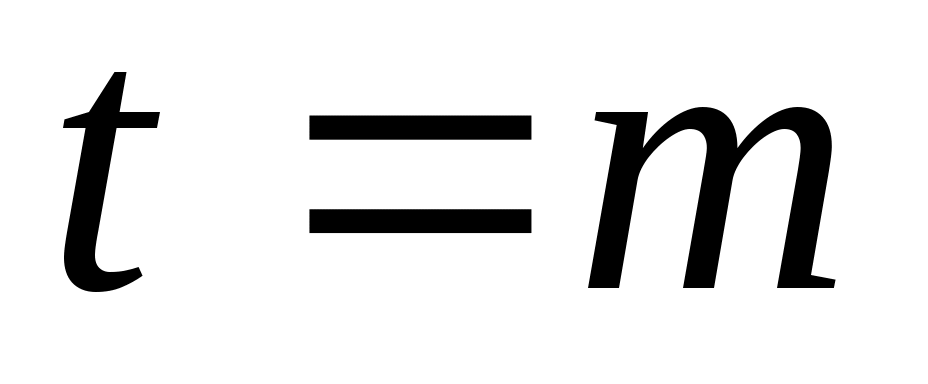 .
.
Чтобы проверить детали (10), (ll) и (12), отметим, что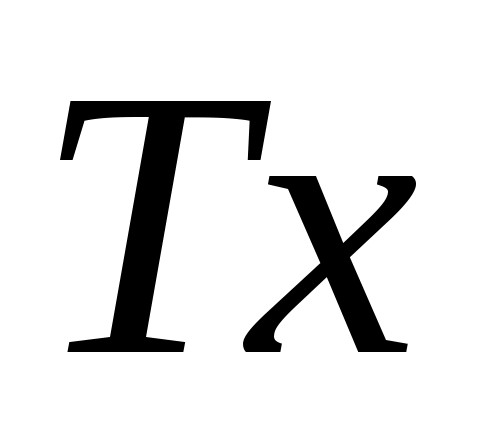 является столбцом компонентов
является столбцом компонентов 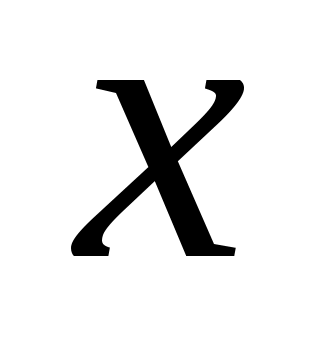 в базисе
в базисе 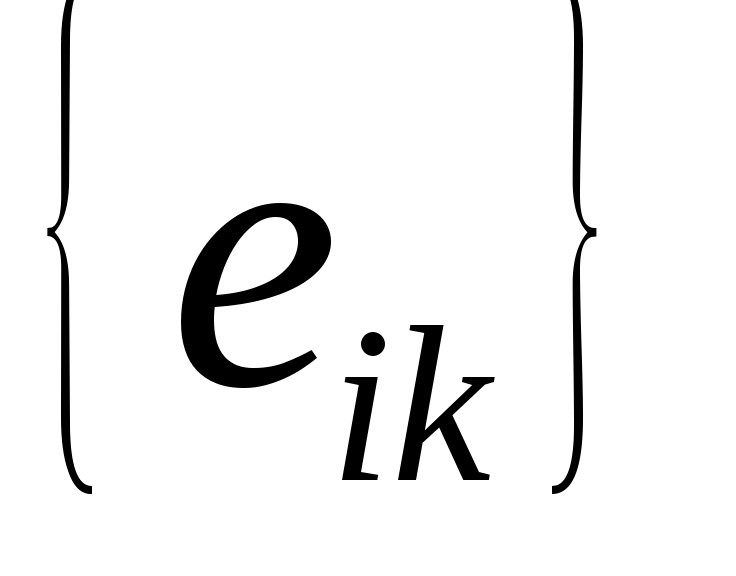 .
.
Таким образом,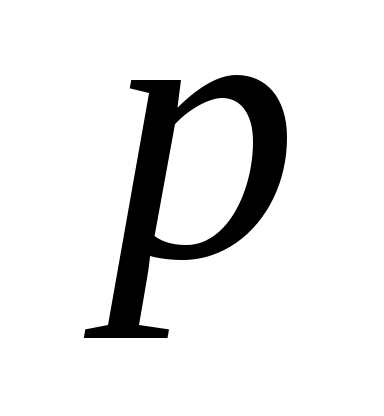 -й столбец
-й столбец 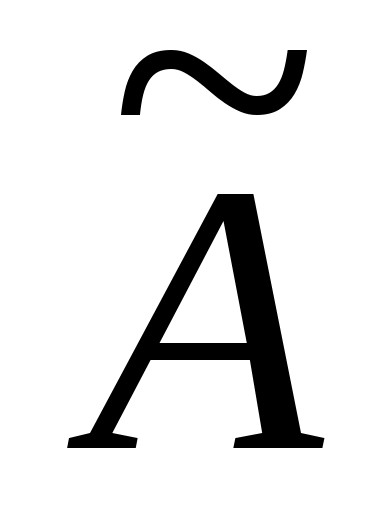 - это список компонентов, в этом базисе,
- это список компонентов, в этом базисе, 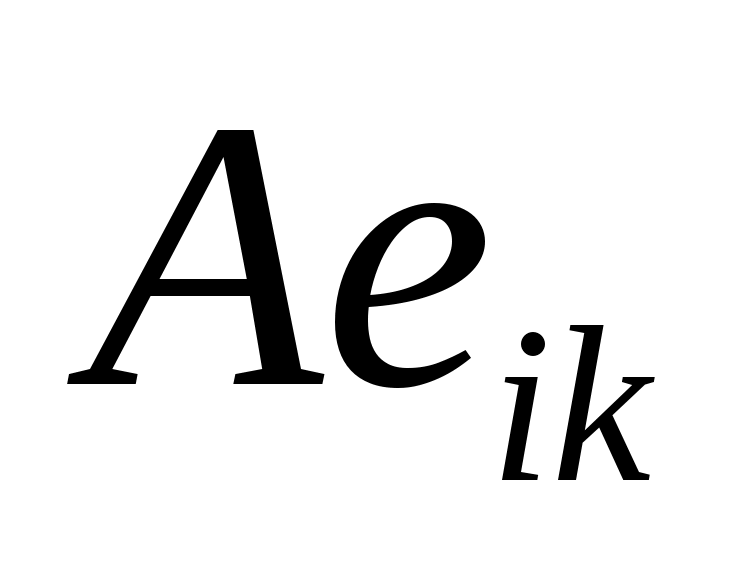
, где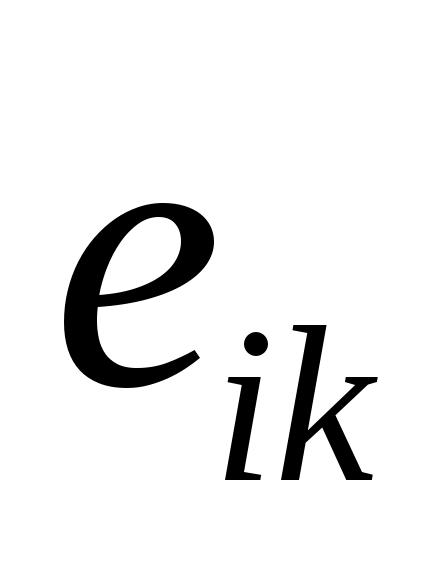 - это
- это 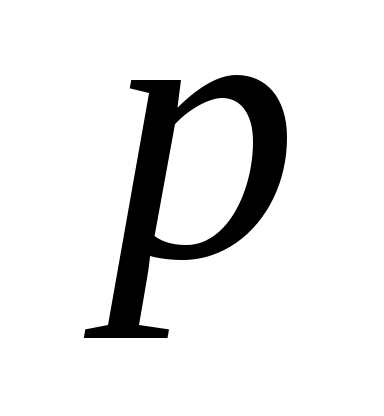 -й базисный вектор. Этот список можно прочитать из (9). Аналогично
-й базисный вектор. Этот список можно прочитать из (9). Аналогично 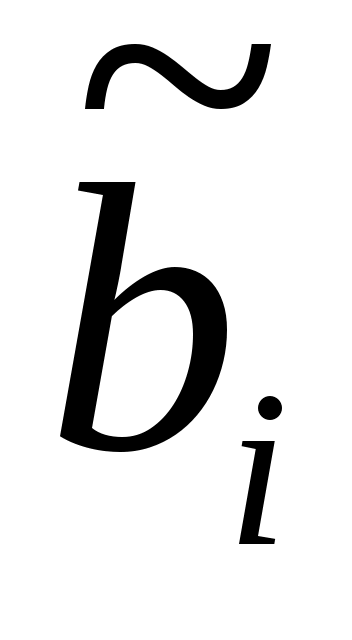 является столбцом компонент
является столбцом компонент 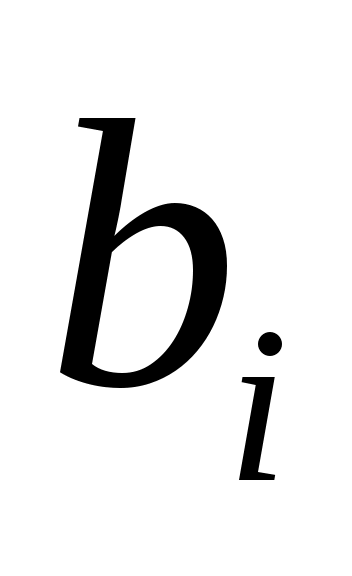 , так что (12) сразу следует из (8b).
, так что (12) сразу следует из (8b).
С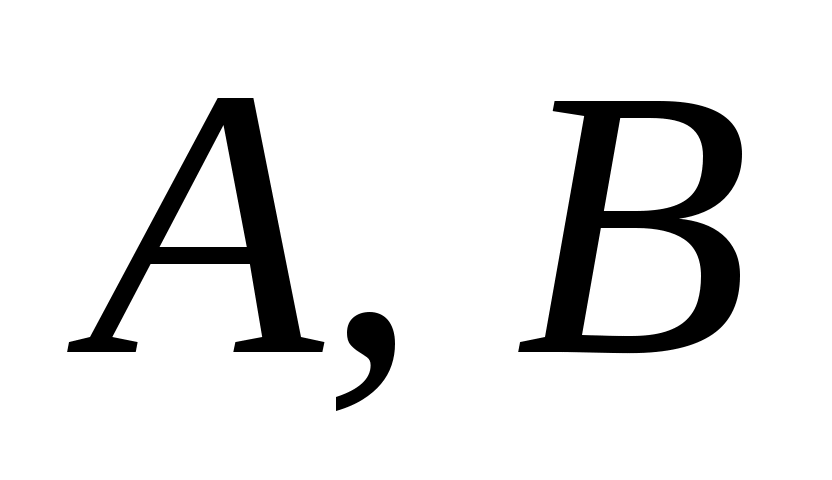 в канонической форме будет в конечном итоге показано, что собственные значения
в канонической форме будет в конечном итоге показано, что собственные значения 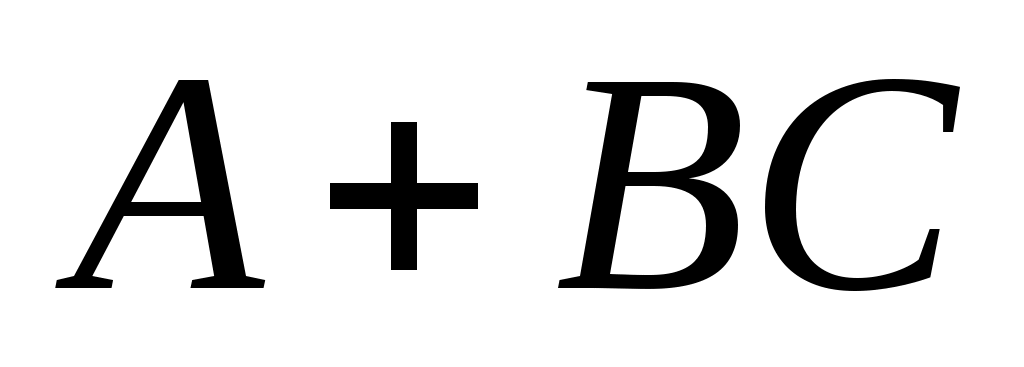 могут быть заданы произвольно. Положим
могут быть заданы произвольно. Положим 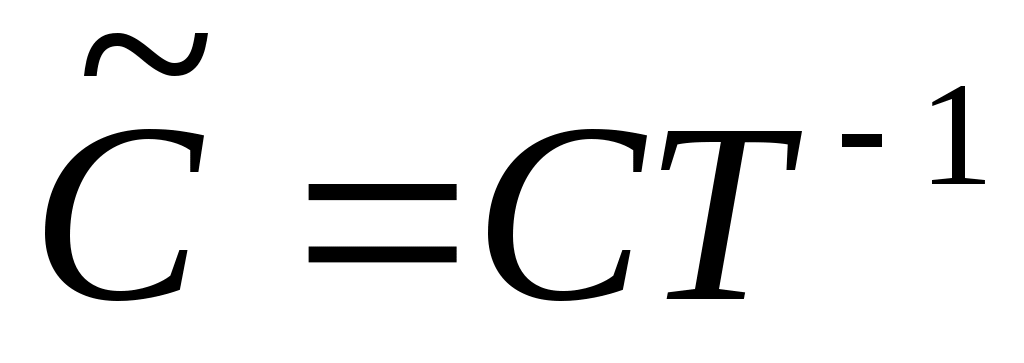 и наблюдаем, что матрица
и наблюдаем, что матрица 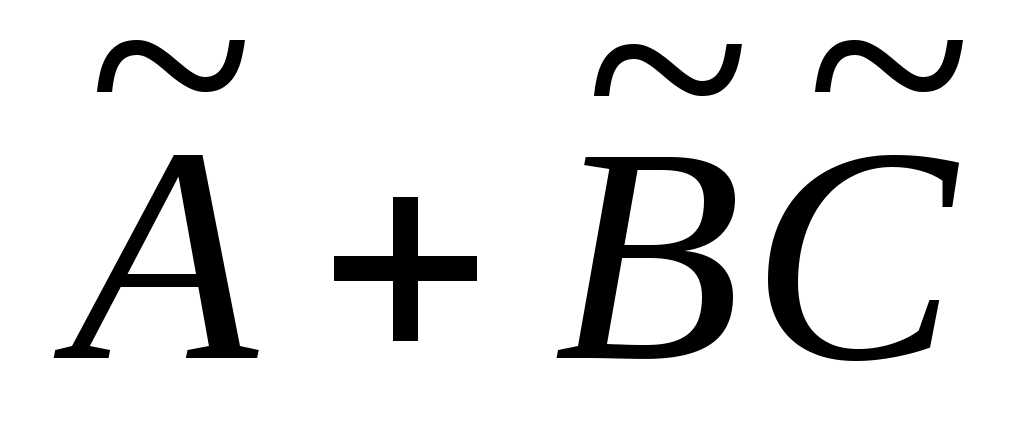 подобна под
подобна под 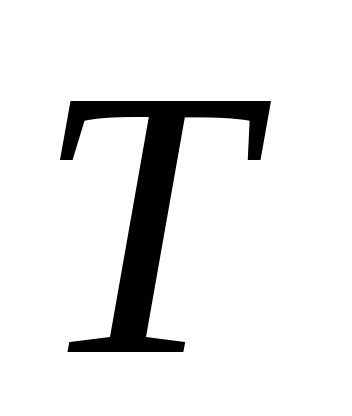 к
к 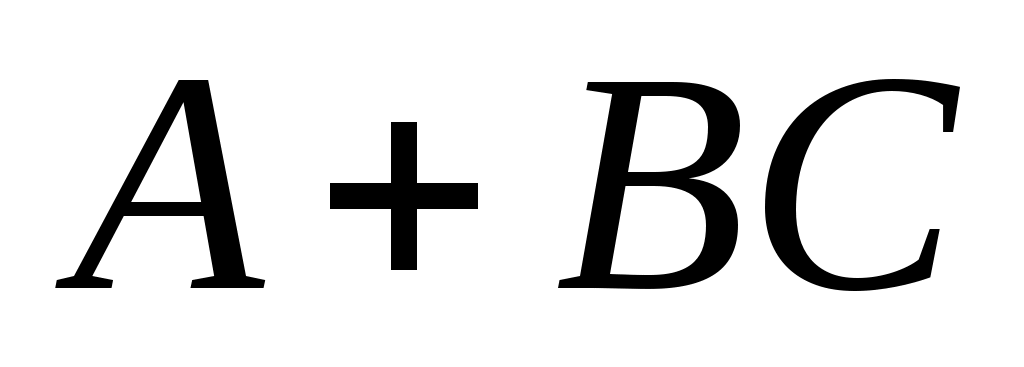 . Далее возьмите
. Далее возьмите 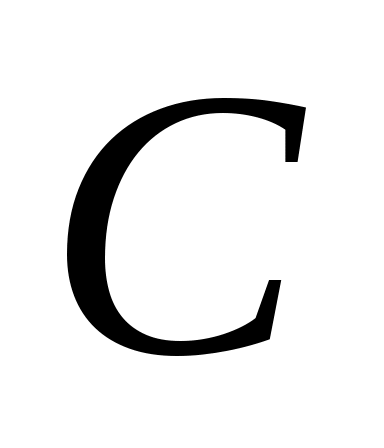 в виде
в виде
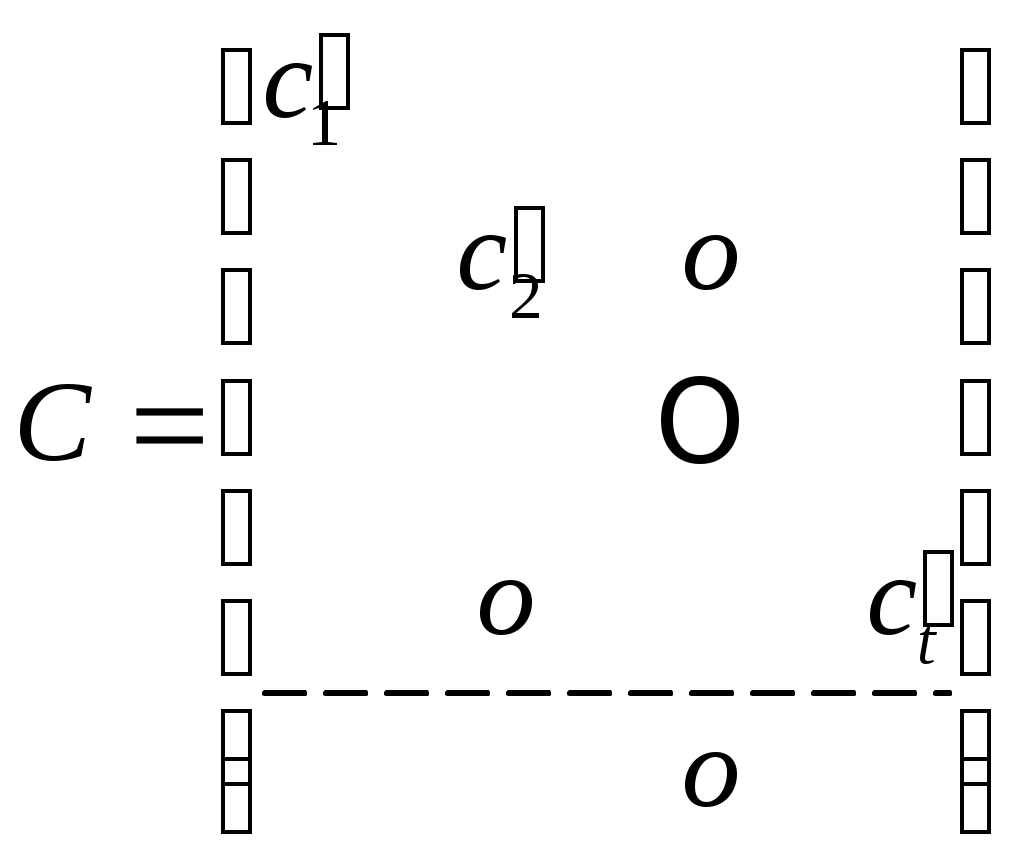 (13)
(13)
где
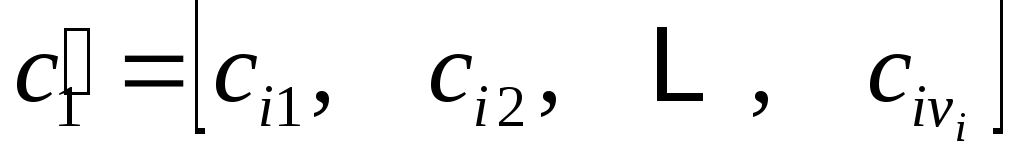 ,
, 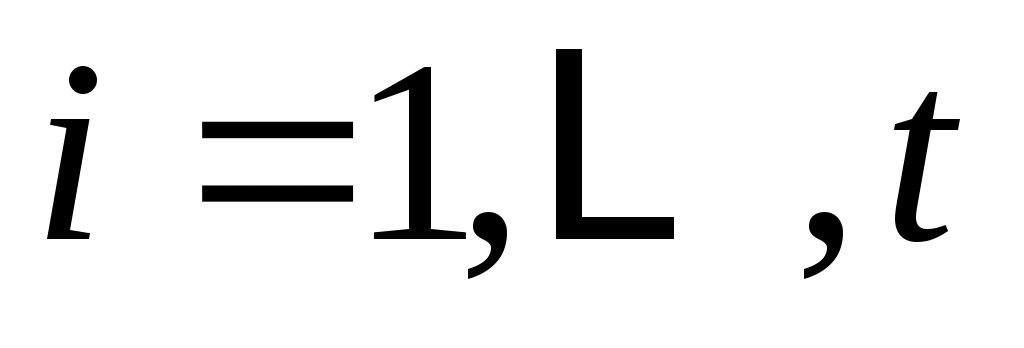 .
.
В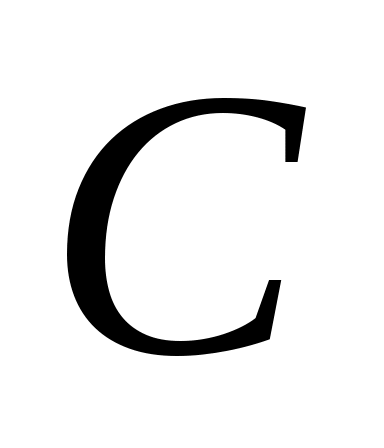 верхний блок имеет размерность
верхний блок имеет размерность 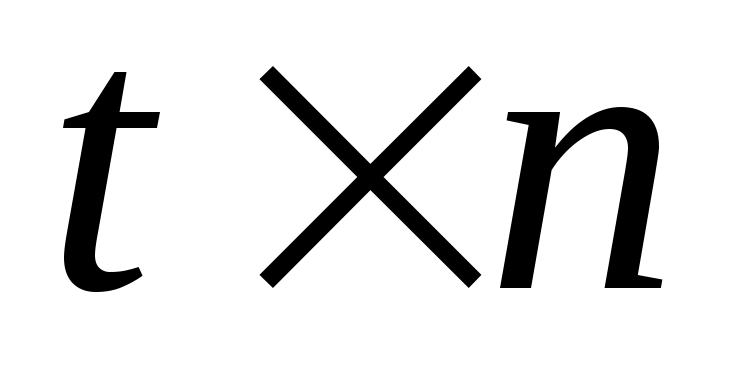 , а нижний блок размера
, а нижний блок размера 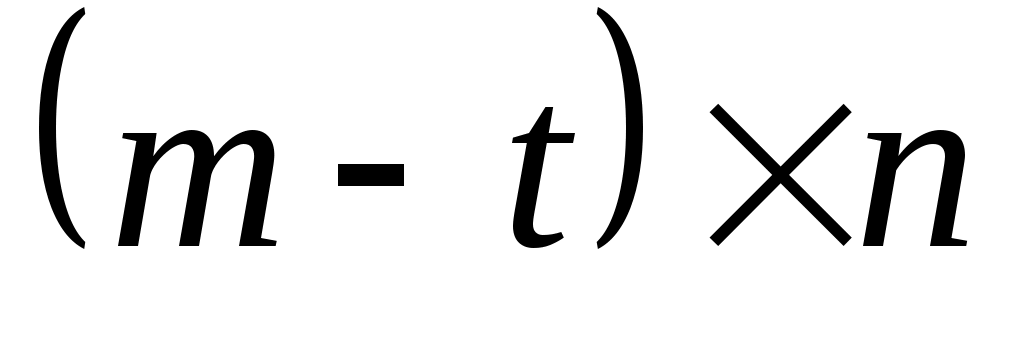 . Из (10)- (13) видно, что
. Из (10)- (13) видно, что
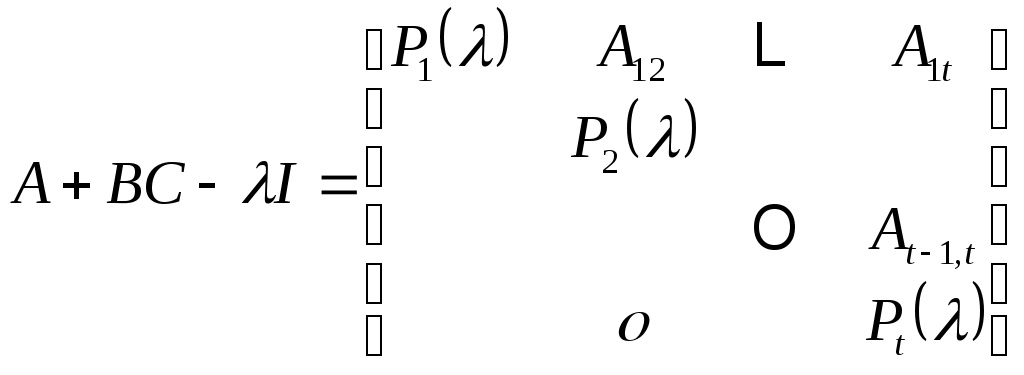
где, для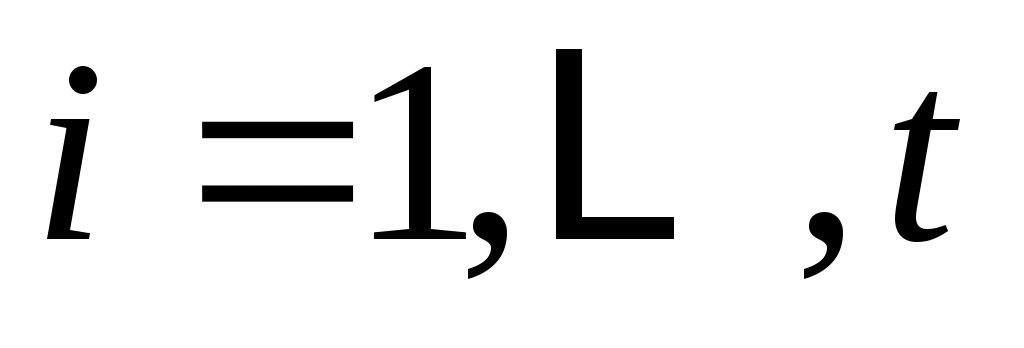 ,
,
 .
.
Пусть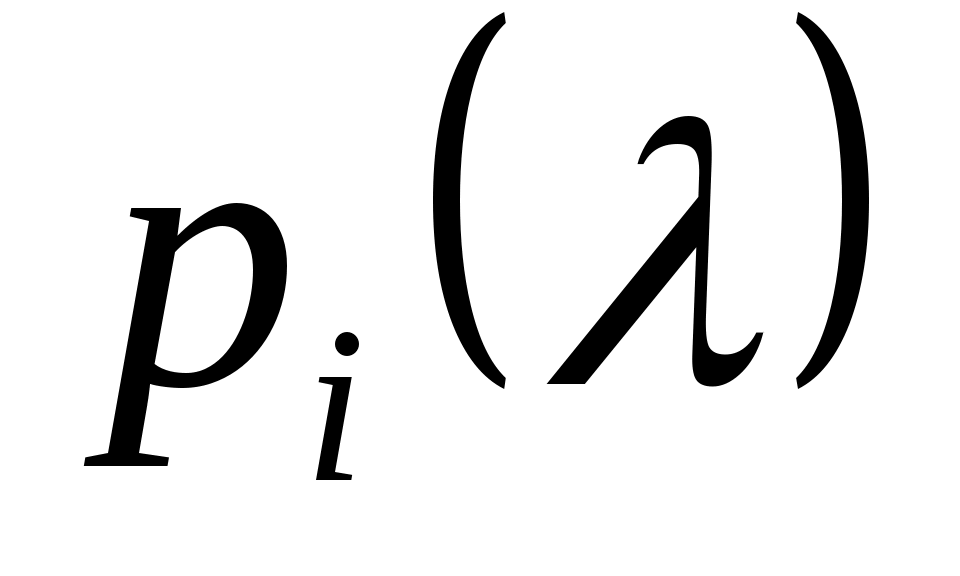 будет определителем
будет определителем 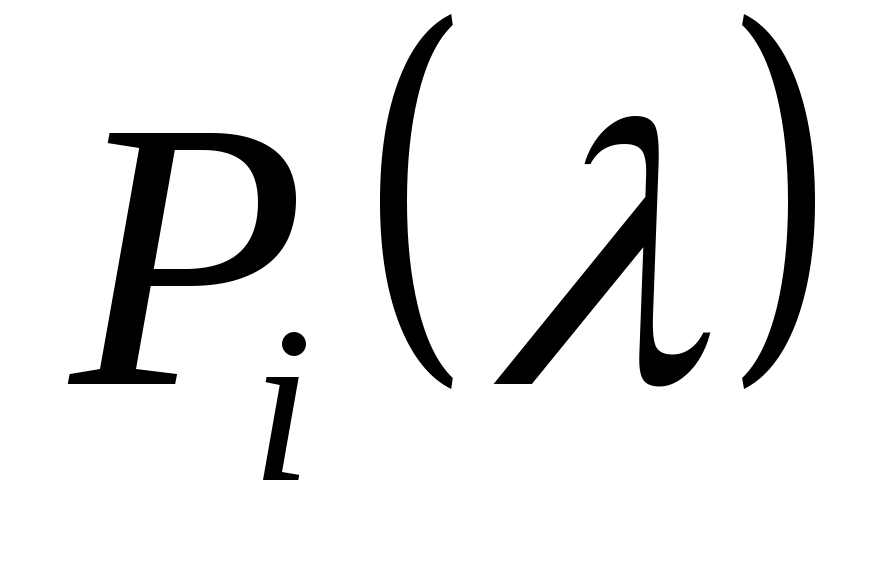 , то есть
, то есть
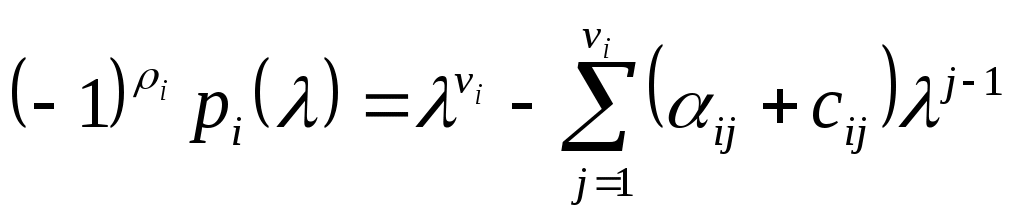 . (14)
. (14)
Из треугольной формы
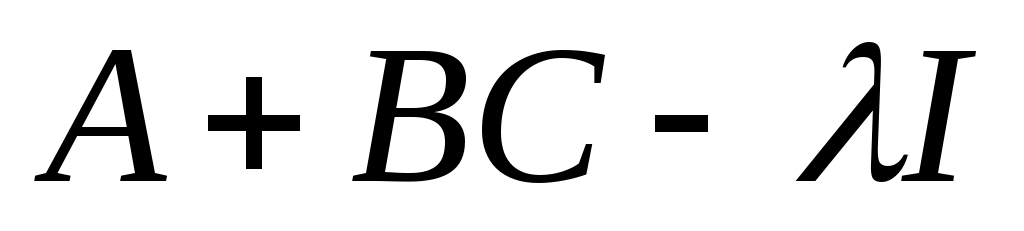 следует, что
следует, что
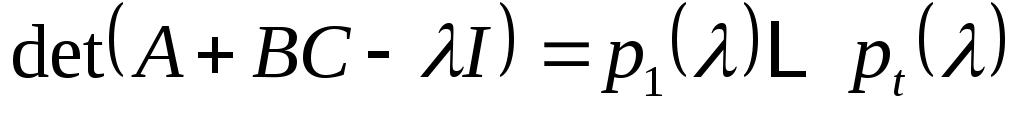 .
.
Также из (14) ясно, что нули числа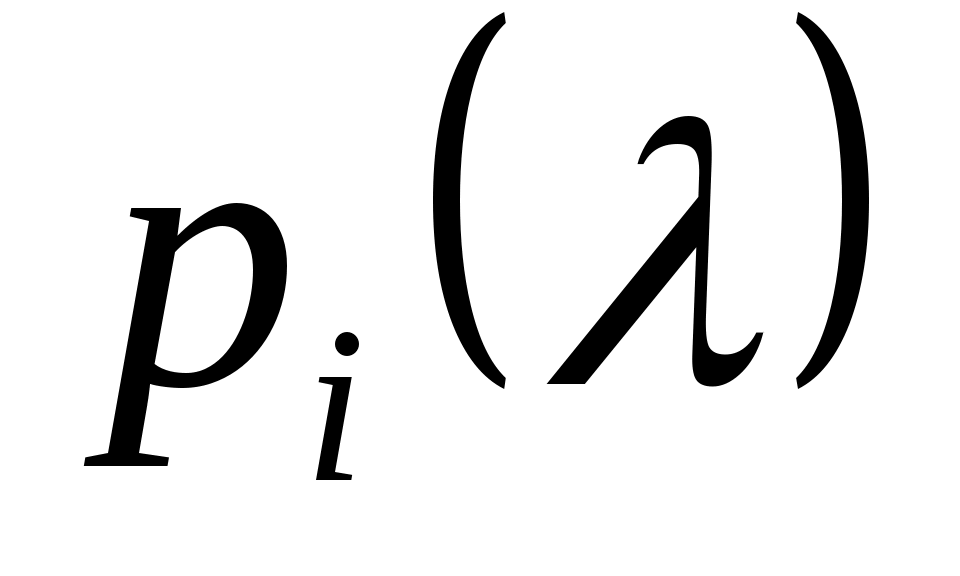 могут быть назначены произвольно (при условии сопряженности комплексных нулей) путем правильного выбора действительных коэффициентов
могут быть назначены произвольно (при условии сопряженности комплексных нулей) путем правильного выбора действительных коэффициентов 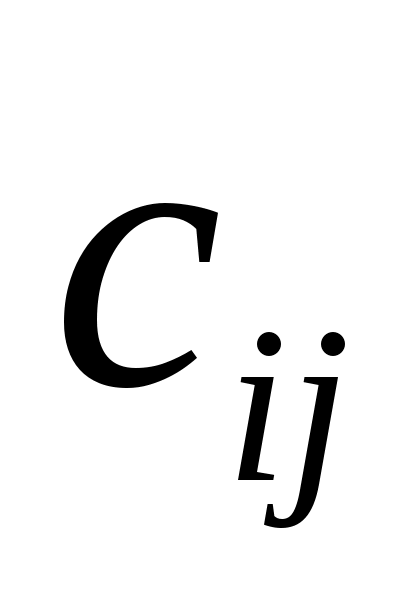 . Это показывает, что, в частности, система (1) всегда может быть стабилизирована путем соответствующего выбора
. Это показывает, что, в частности, система (1) всегда может быть стабилизирована путем соответствующего выбора 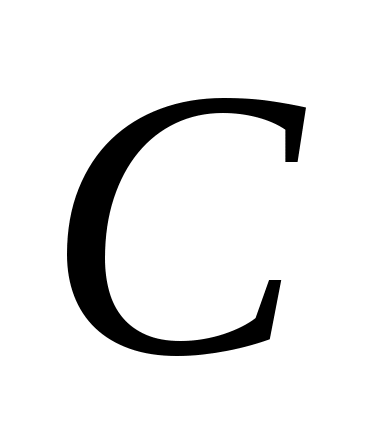 .
.
Чтобы показать, что может быть назначен произвольный набор собственных значений , необходимо учитывать тот факт, что матрицы
, необходимо учитывать тот факт, что матрицы 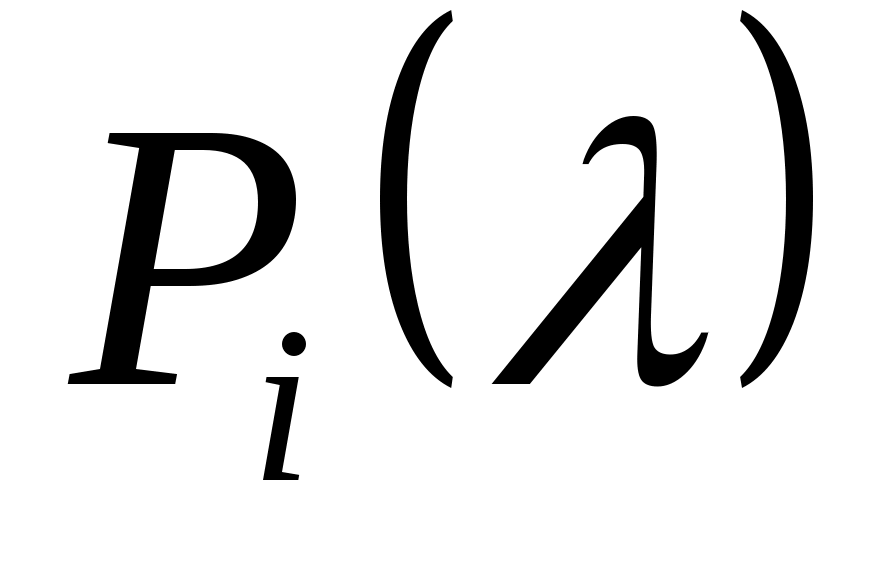 имеют фиксированную размерность. Если, например,
имеют фиксированную размерность. Если, например, 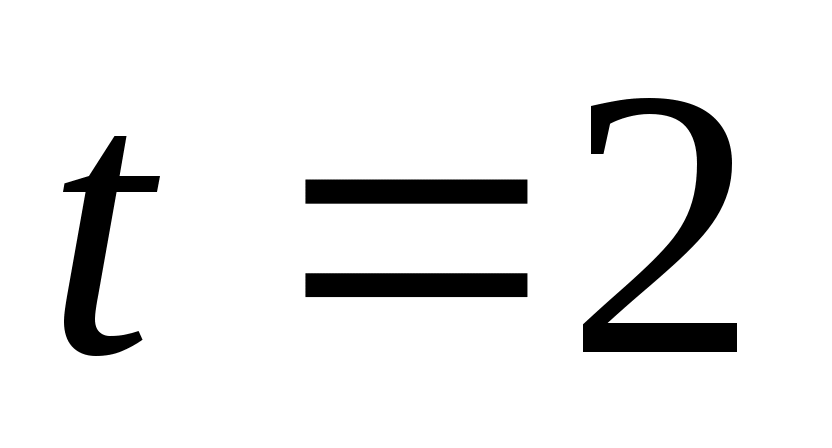 и
и 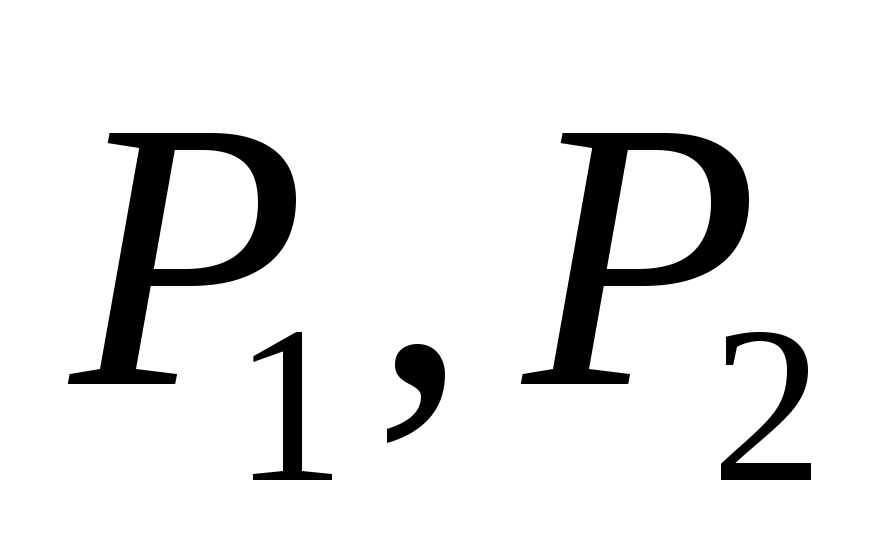 каждый имеют размерность
каждый имеют размерность 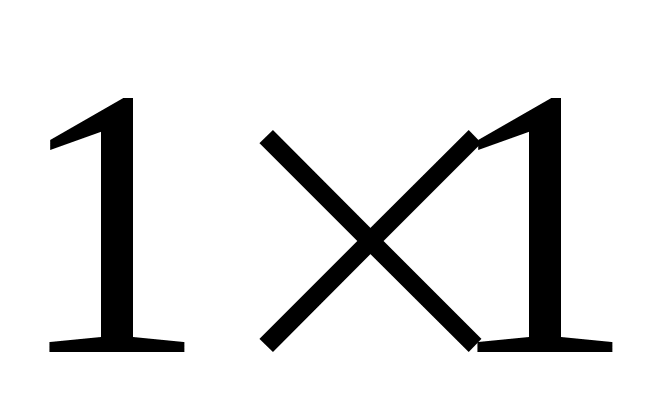 , невозможно назначить произвольную комплексную пару собственных значений путем независимой регулировки
, невозможно назначить произвольную комплексную пару собственных значений путем независимой регулировки 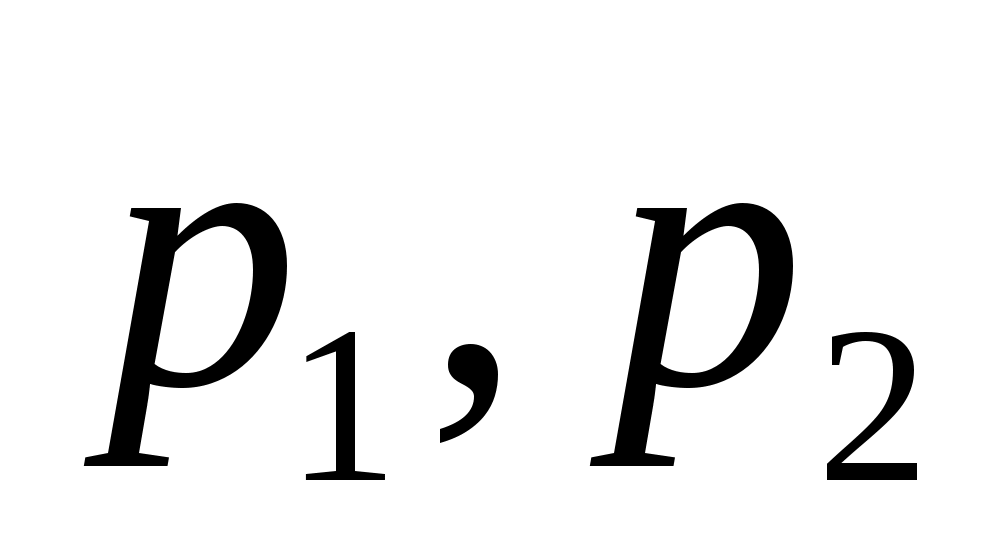 . Это дополнительная сложность, связанная с ограничением реальных параметров. Для продолжения пусть
. Это дополнительная сложность, связанная с ограничением реальных параметров. Для продолжения пусть 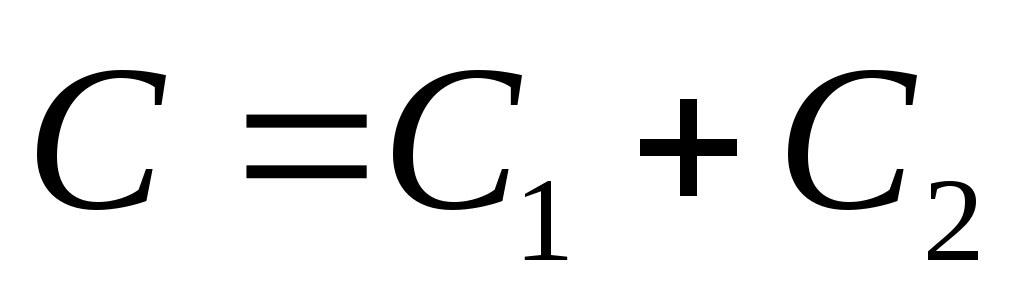 , где
, где 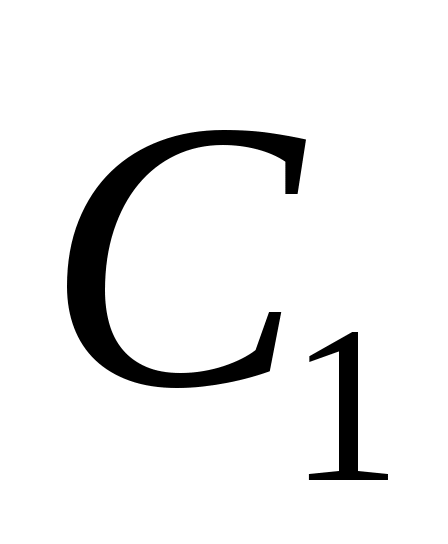 имеет вид (13) и подчиняется только требованию, чтобы все собственные значения
имеет вид (13) и подчиняется только требованию, чтобы все собственные значения 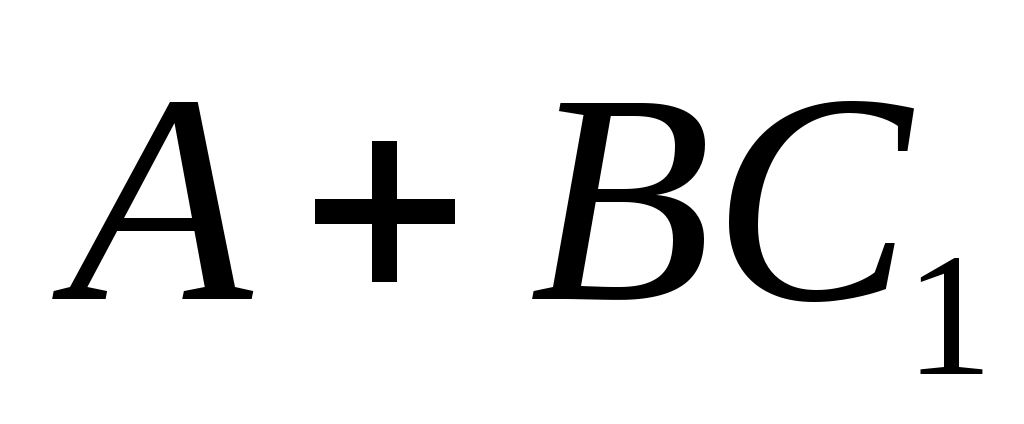 были различны. Только что было замечено, что такой выбор
были различны. Только что было замечено, что такой выбор 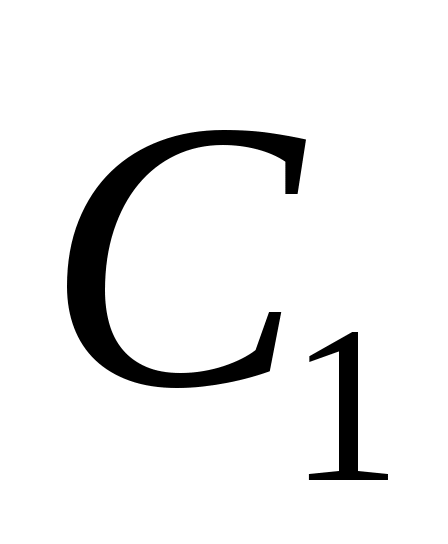 возможен. Тогда по лемме 1 пространство
возможен. Тогда по лемме 1 пространство  циклически относительно матрицы
циклически относительно матрицы 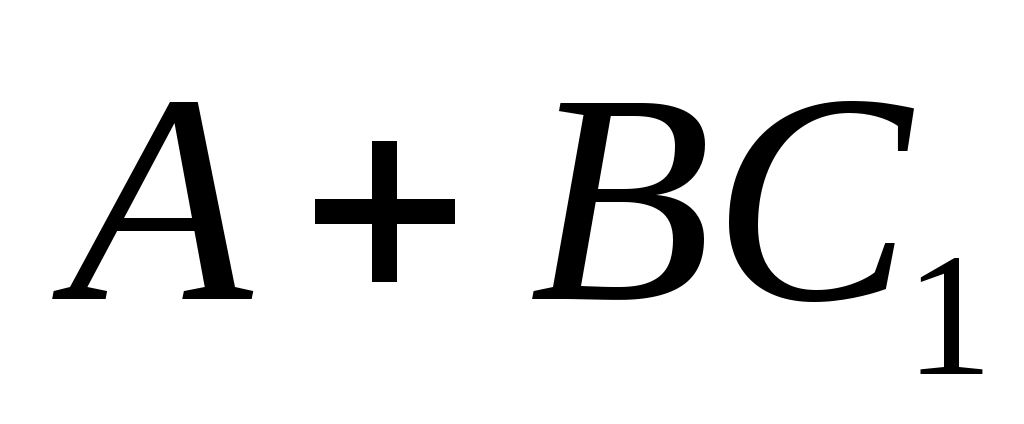
. По лемме 4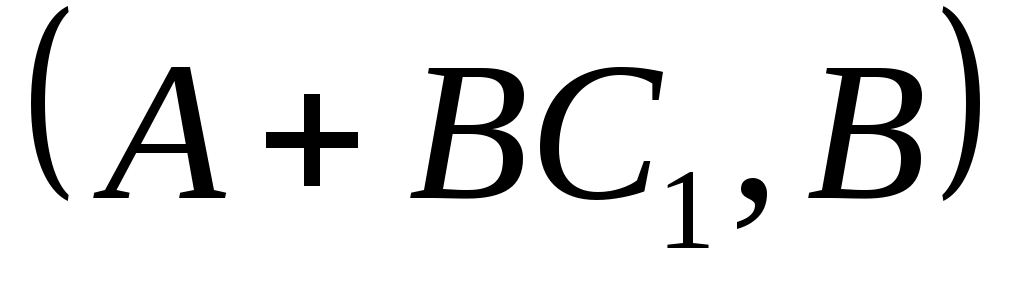 является управляемым. Применяя лемму 3, можно найти
является управляемым. Применяя лемму 3, можно найти 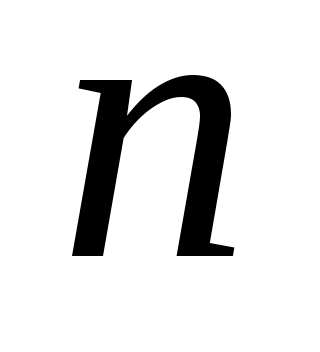 -вектор
-вектор 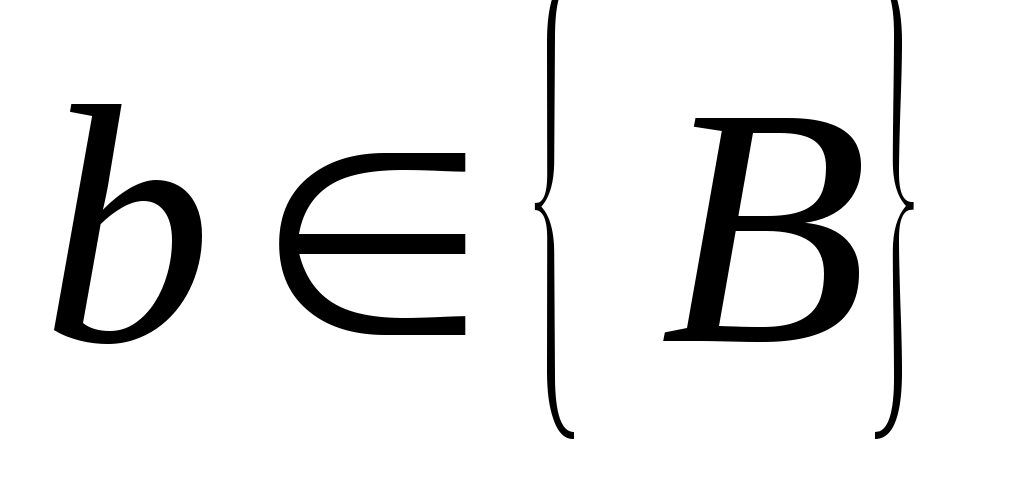 такой, что
такой, что 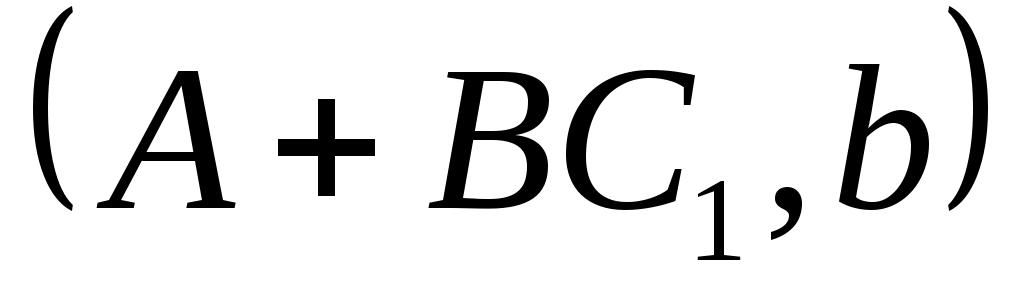 является управляемым. Теперь
является управляемым. Теперь 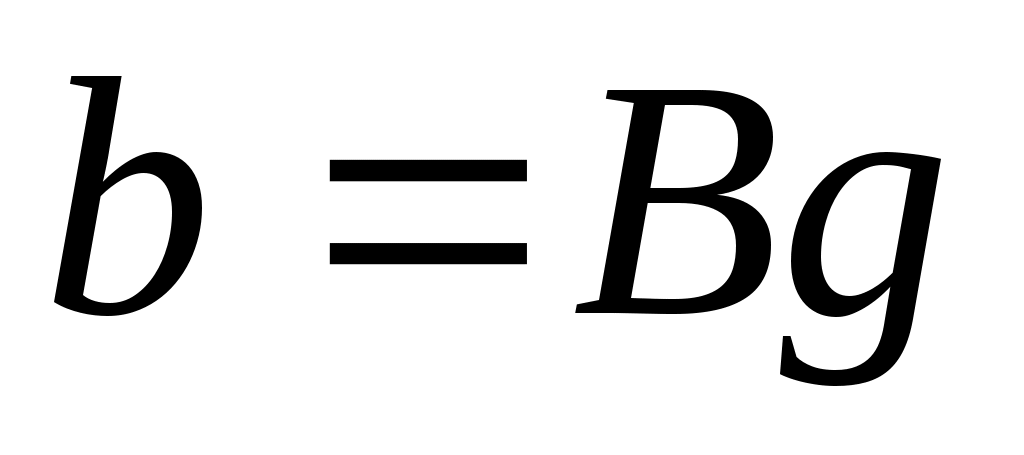 для подходящей
для подходящей 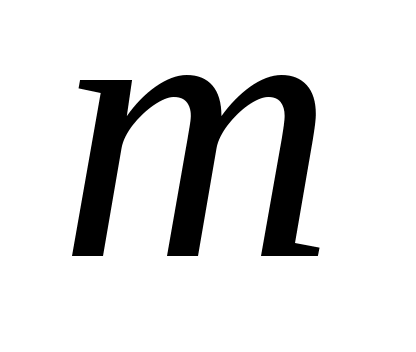 вектор
вектор 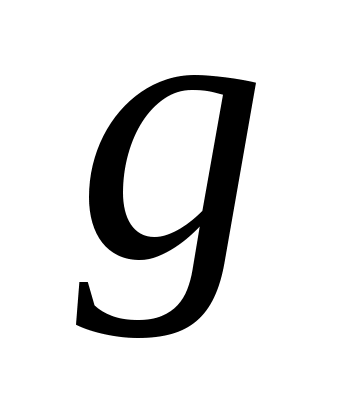 . Таким образом, если
. Таким образом, если  принимается в виде
принимается в виде
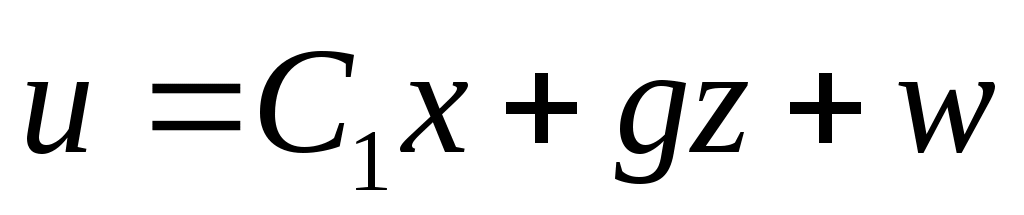
с скаляром и вектором
скаляром и вектором 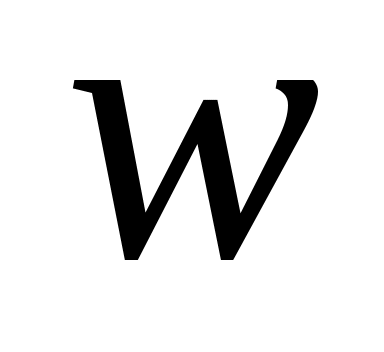
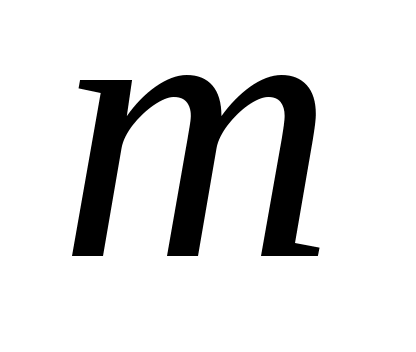 , то система (1) становится
, то система (1) становится
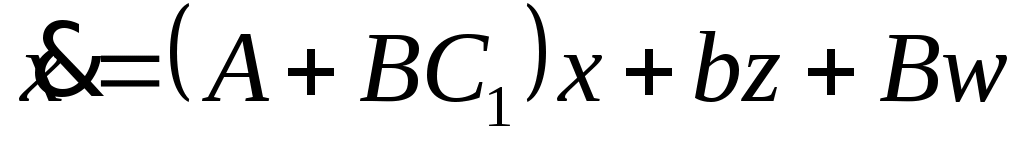 .
.
Наконец, поскольку теорема верна в случае с одним входом, можно выбрать в виде
можно выбрать в виде
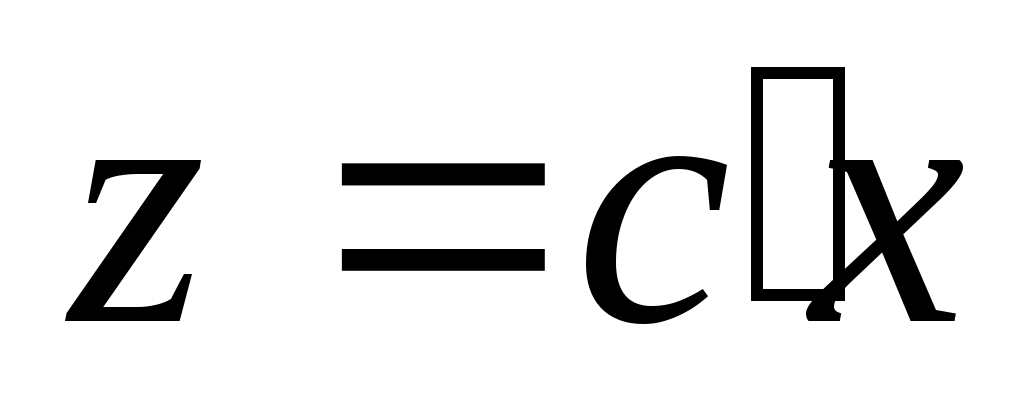
таким образом, что матрица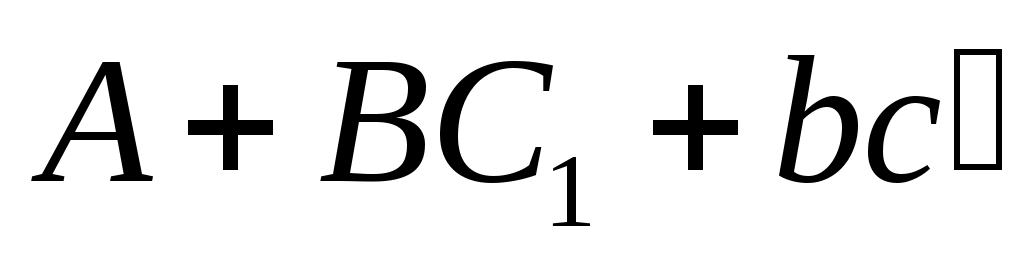 имеет требуемый набор собственных значений
имеет требуемый набор собственных значений  . То есть матрица «усиления»
. То есть матрица «усиления»
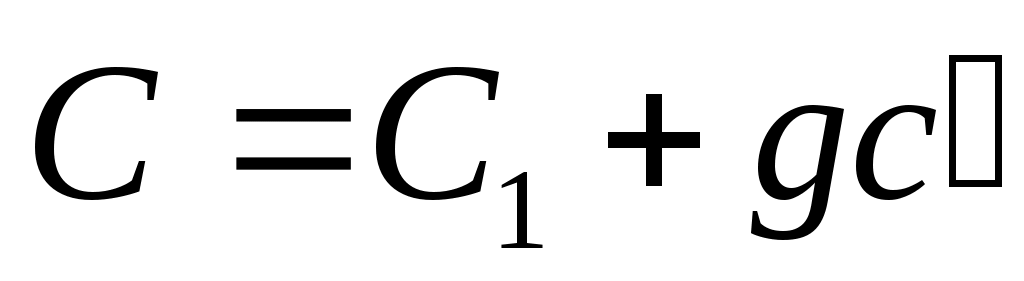
имеет обязательное свойство. Теорема доказана.
Комментарии
1) Конструкцию в доказательстве необходимости можно суммировать в терминах блок-схемы (рис.1). После выбора подходящего набора переменных состояния (каноническая форма (8) - (12)) конструктор строит внутренний цикл обратной связи (через матрицу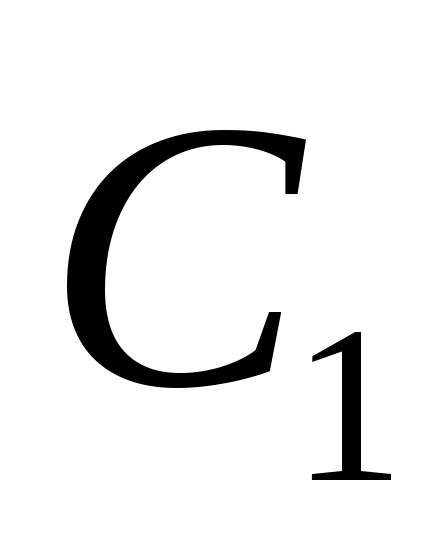 ), который делает систему циклической, то есть управляемой одним входом. Затем разработчик выбирает подходящий ввод в виде
), который делает систему циклической, то есть управляемой одним входом. Затем разработчик выбирает подходящий ввод в виде 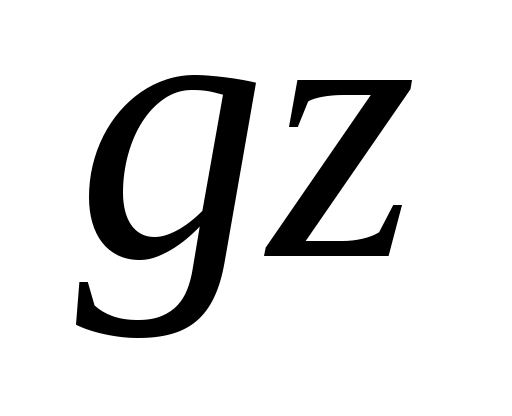 (
(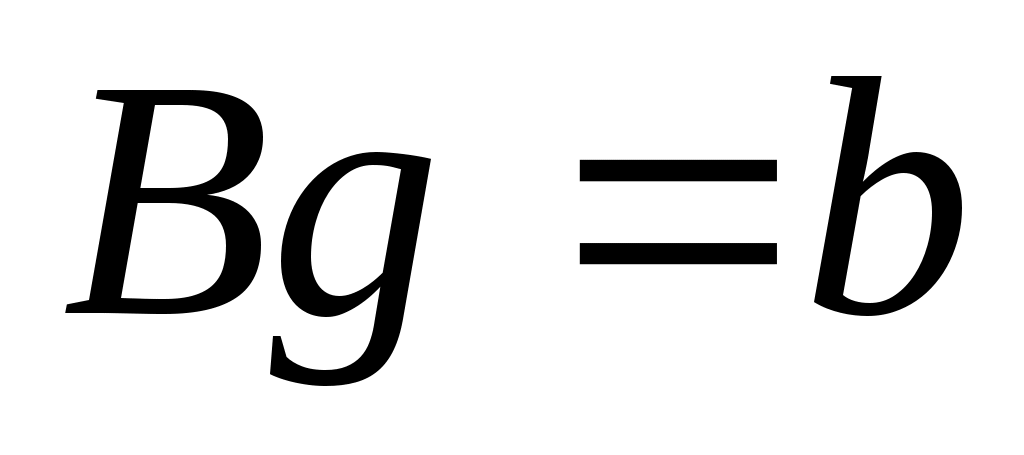 -генератор
-генератор  ) и завершает внешний цикл, устанавливая
) и завершает внешний цикл, устанавливая 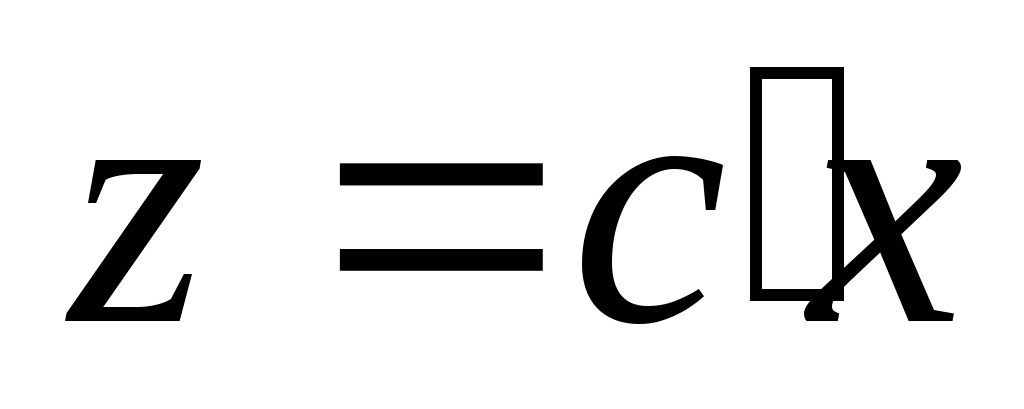 для достижения требуемого размещения полюсов.
для достижения требуемого размещения полюсов.
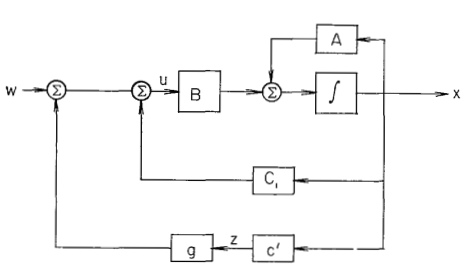
Рисунок 1. Построение в доказательстве после выбора канонических переменных состояния.
2) На практике может быть много способов выбора переменных состояния и величин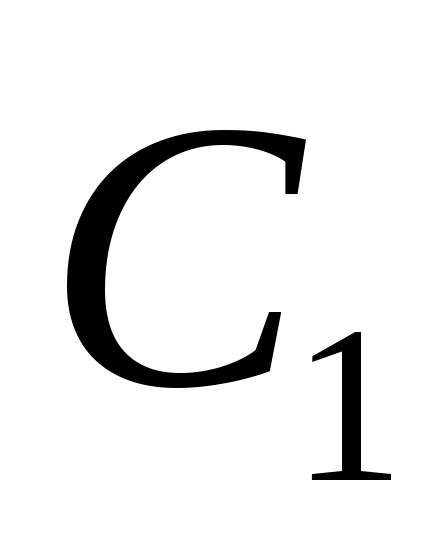 ,
, 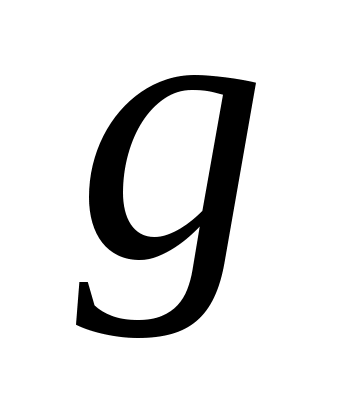 ,
, 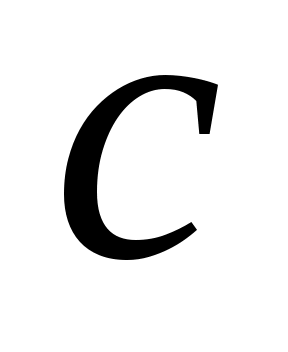 для достижения заданного назначения полюсов. Использование этой свободы с помощью подходящих критериев проектирования является интересной проблемой современных исследований [5].
для достижения заданного назначения полюсов. Использование этой свободы с помощью подходящих критериев проектирования является интересной проблемой современных исследований [5].
3) Стоит отметить, что для данной пары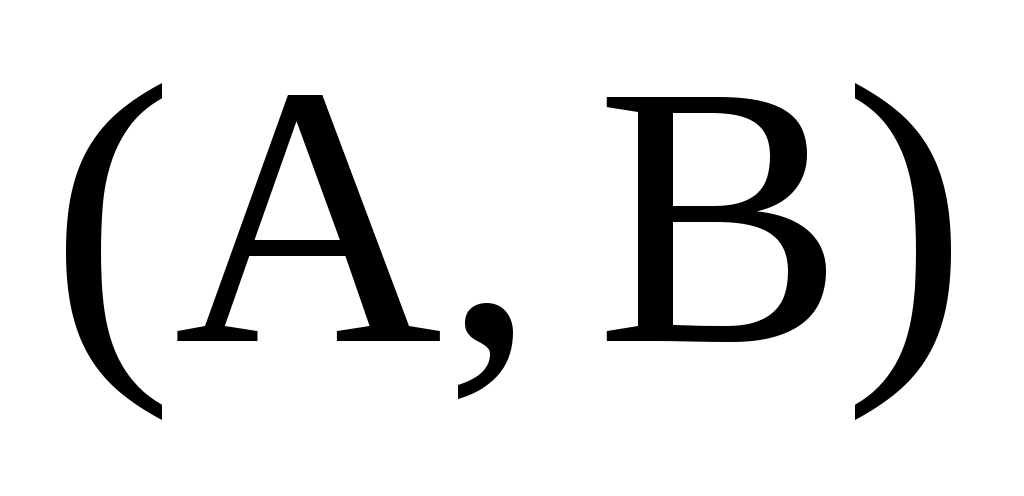 может существовать более одной «канонической» формы (10)-(12). То есть матрица
может существовать более одной «канонической» формы (10)-(12). То есть матрица 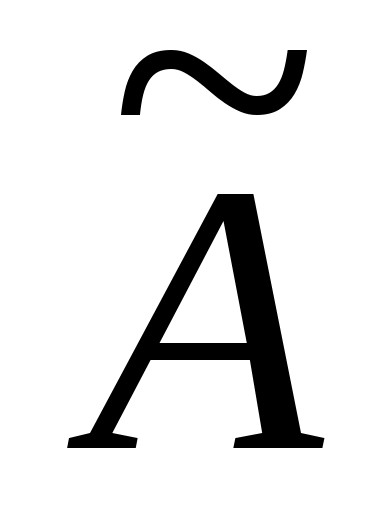 в (10) может не раскрывать внутреннюю структуру
в (10) может не раскрывать внутреннюю структуру  , как это делают обычные рациональные канонические разложения в блочно-диагональные формы [3]. Недостаток таких блочно-диагональных представлений состоит в том, что, как правило, циклические подпространства, соответствующие отдельным блокам, не обязательно должны иметь образующие в подпространстве
, как это делают обычные рациональные канонические разложения в блочно-диагональные формы [3]. Недостаток таких блочно-диагональных представлений состоит в том, что, как правило, циклические подпространства, соответствующие отдельным блокам, не обязательно должны иметь образующие в подпространстве
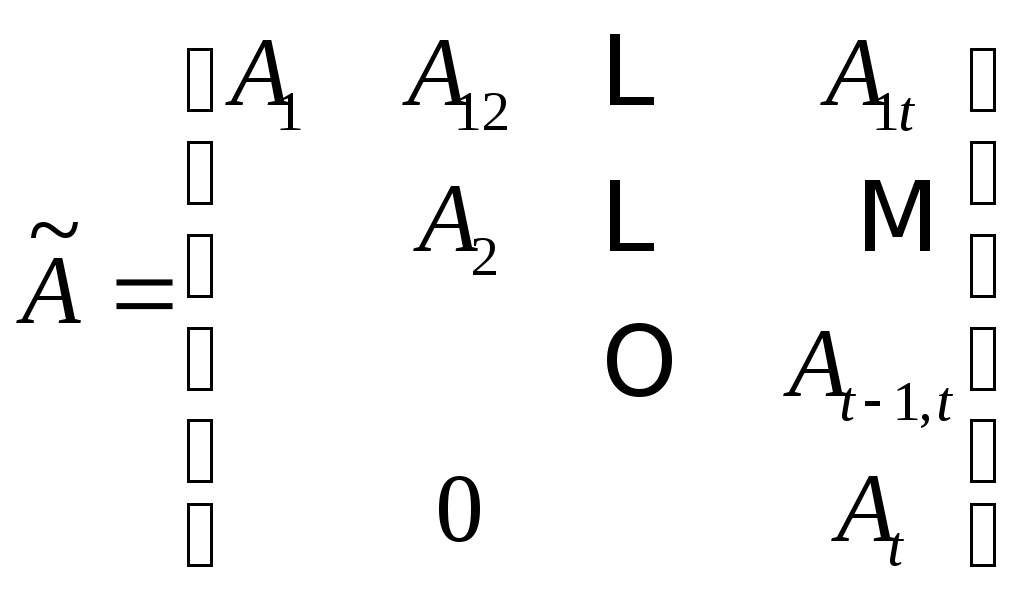 . (10)
. (10)В (10) матрицы
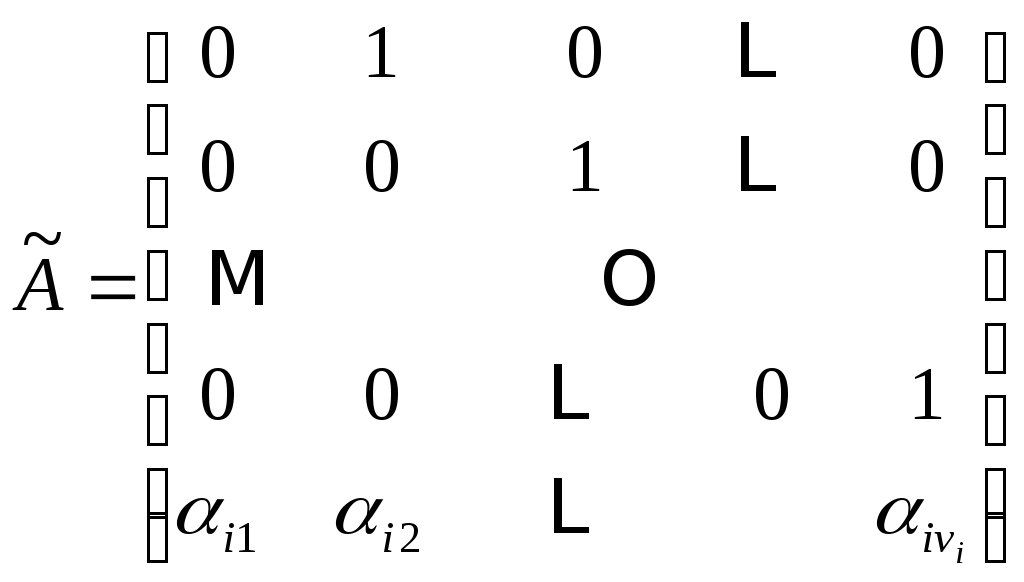 ,
, и матрицы
Наконец,
здесь
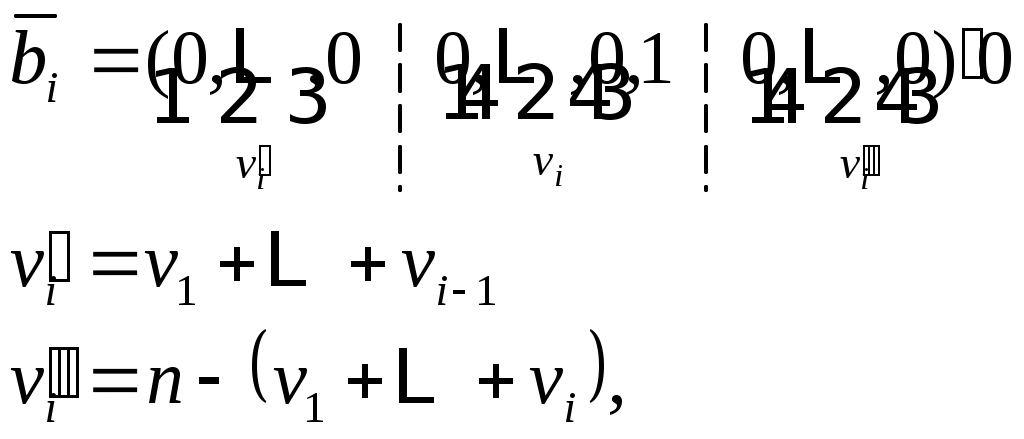 (12b)
(12b)и
Чтобы проверить детали (10), (ll) и (12), отметим, что
Таким образом,
, где
С
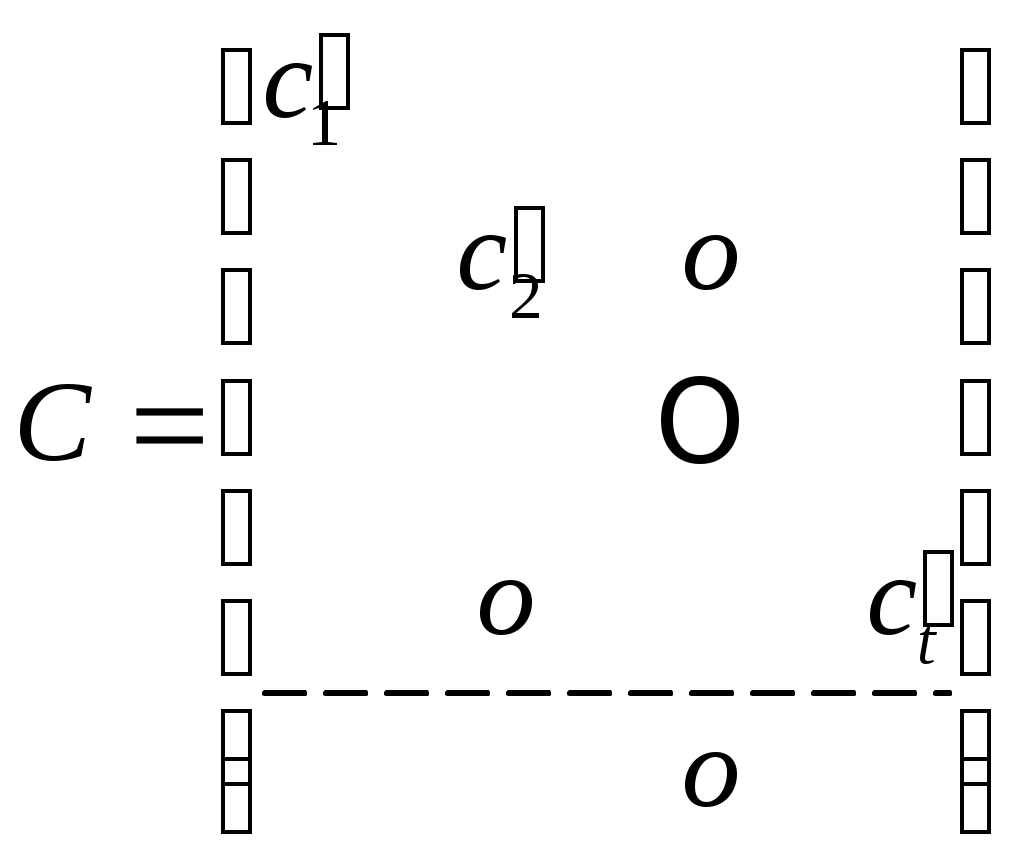 (13)
(13)где
В
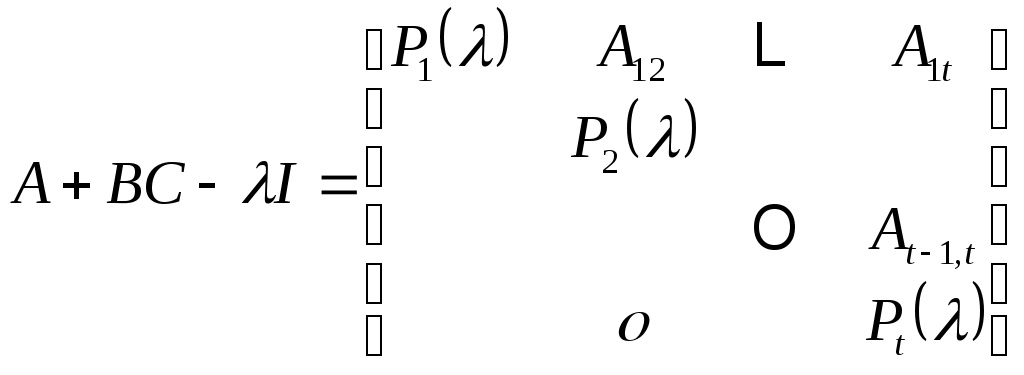
где, для
 .
.Пусть
Из треугольной формы
Также из (14) ясно, что нули числа
Чтобы показать, что может быть назначен произвольный набор собственных значений
. По лемме 4
с
Наконец, поскольку теорема верна в случае с одним входом,
таким образом, что матрица
имеет обязательное свойство. Теорема доказана.
Комментарии
1) Конструкцию в доказательстве необходимости можно суммировать в терминах блок-схемы (рис.1). После выбора подходящего набора переменных состояния (каноническая форма (8) - (12)) конструктор строит внутренний цикл обратной связи (через матрицу

Рисунок 1. Построение в доказательстве после выбора канонических переменных состояния.
2) На практике может быть много способов выбора переменных состояния и величин
3) Стоит отметить, что для данной пары


