Файл: О назначении полюсов в многовходных управляемых линейных системах.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.03.2024
Просмотров: 23
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
с требуемым свойством существуют.
Следующее наблюдение будет полезно; простое доказательство опущено.
ЛЕММА 4: Если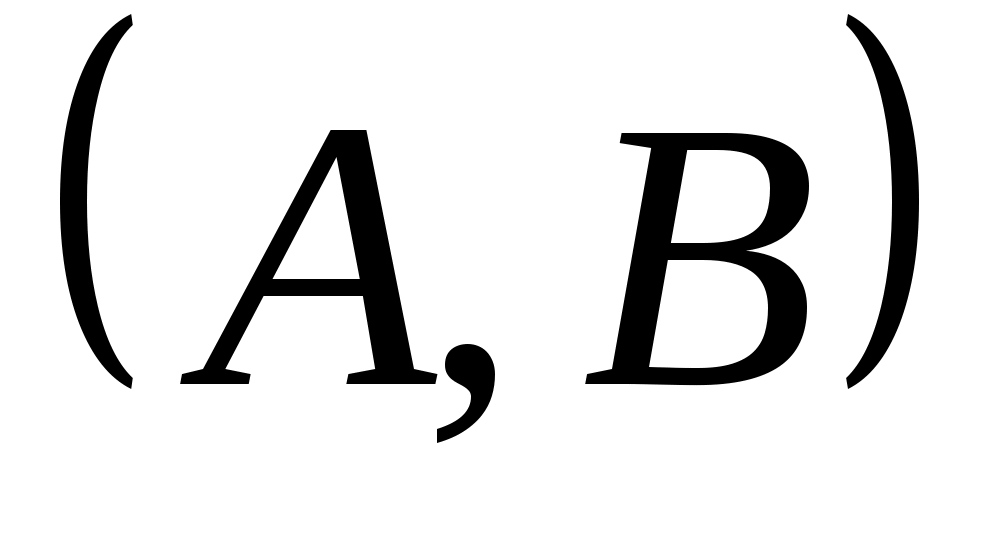 является управляемым и
является управляемым и 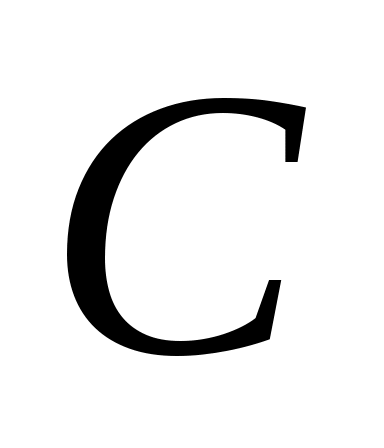 является матрицей
является матрицей 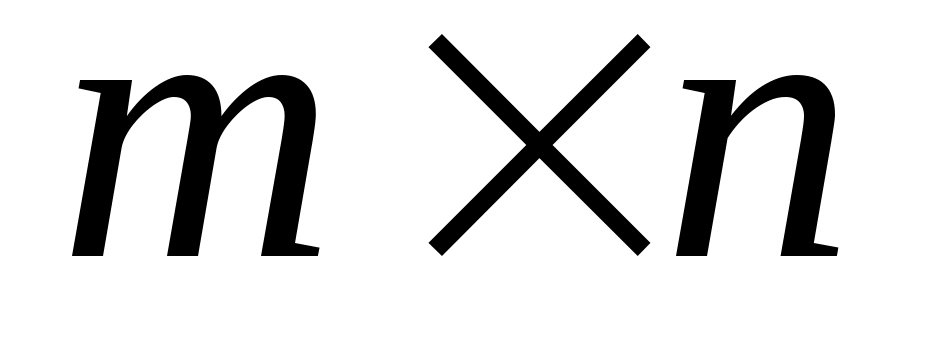 , то
, то 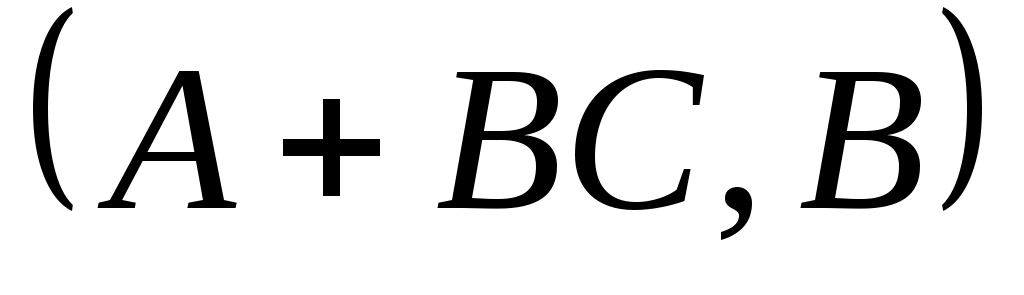 является управляемым.
является управляемым.
Также используется концепция соответствия. Пусть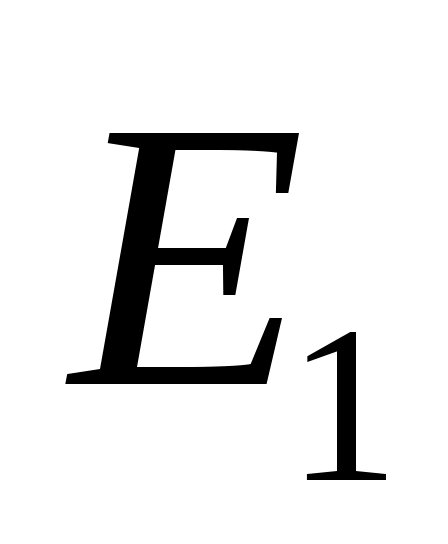 - инвариантное подпространство в
- инвариантное подпространство в  , то есть
, то есть 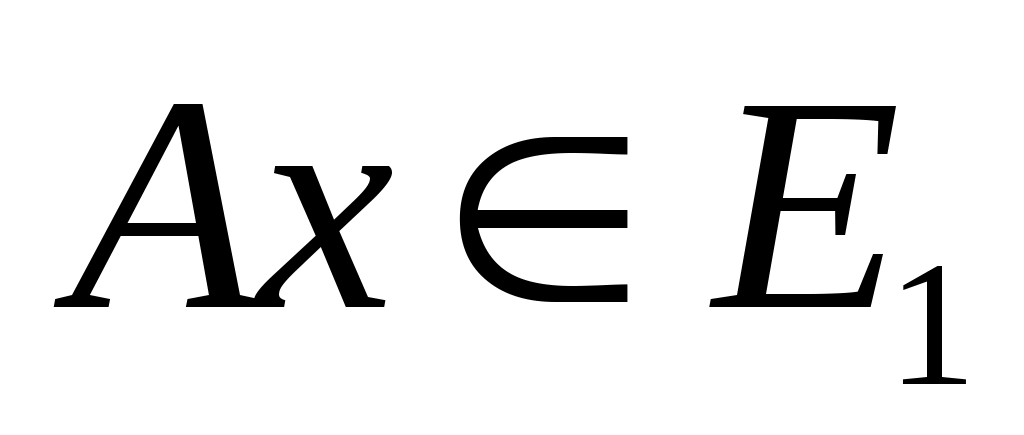 всякий раз, когда
всякий раз, когда 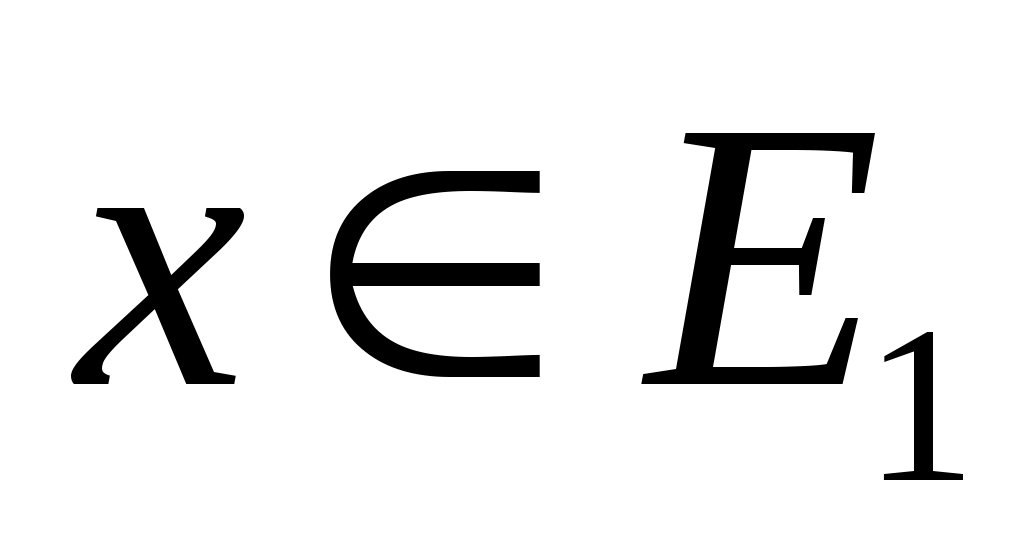 . Подпространство
. Подпространство 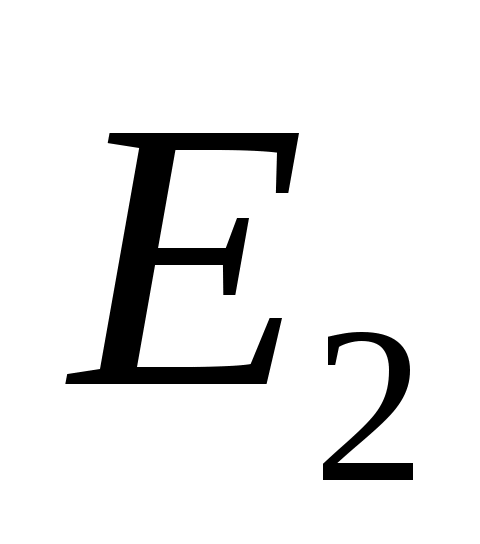 инвариантно
инвариантно 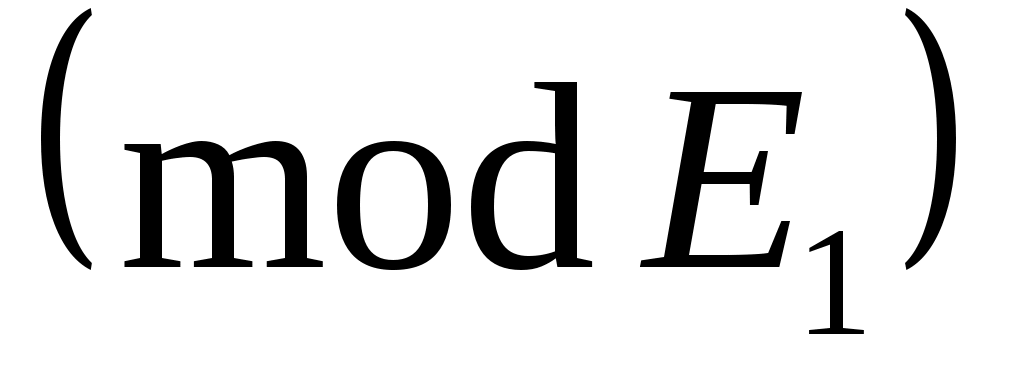 , если
, если 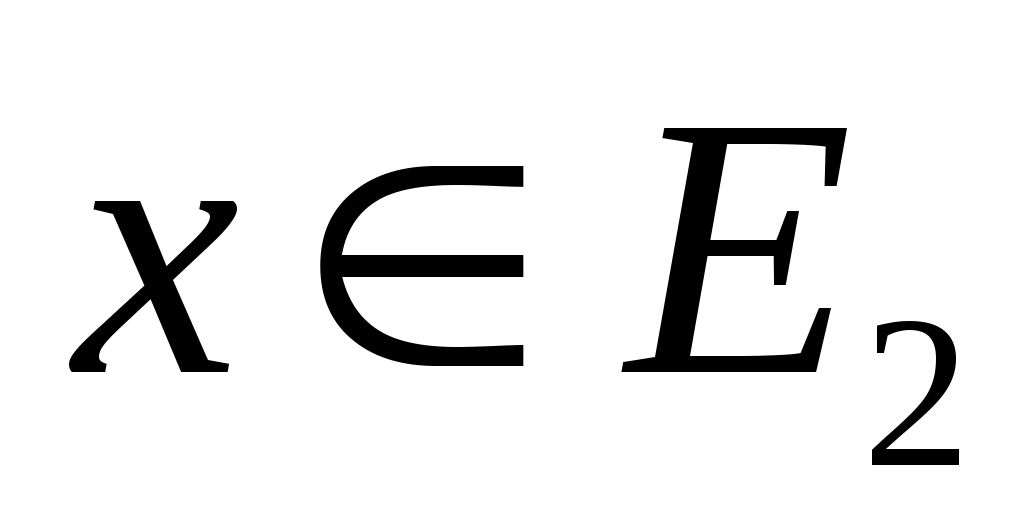 подразумевает
подразумевает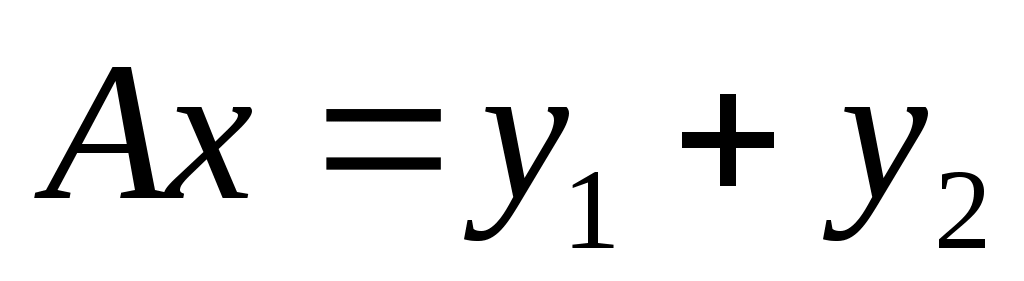 , где
, где 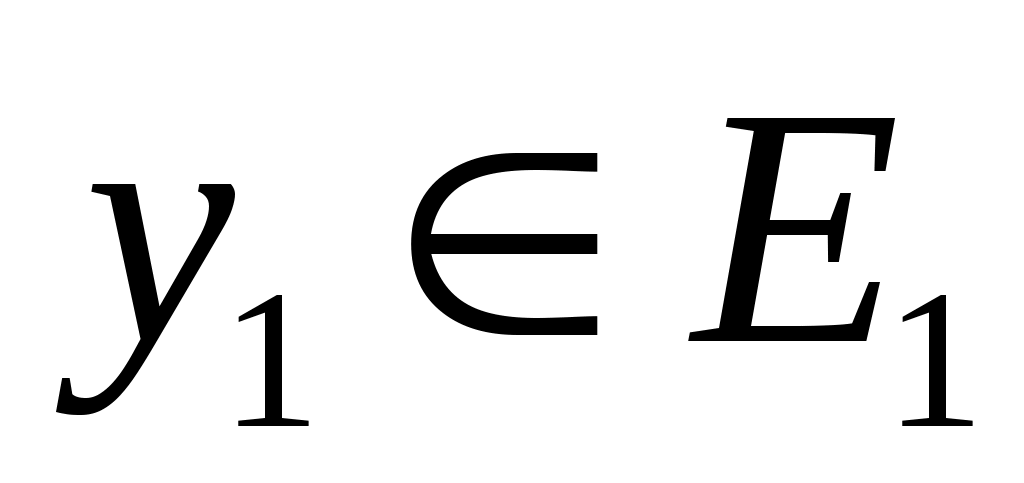 и
и 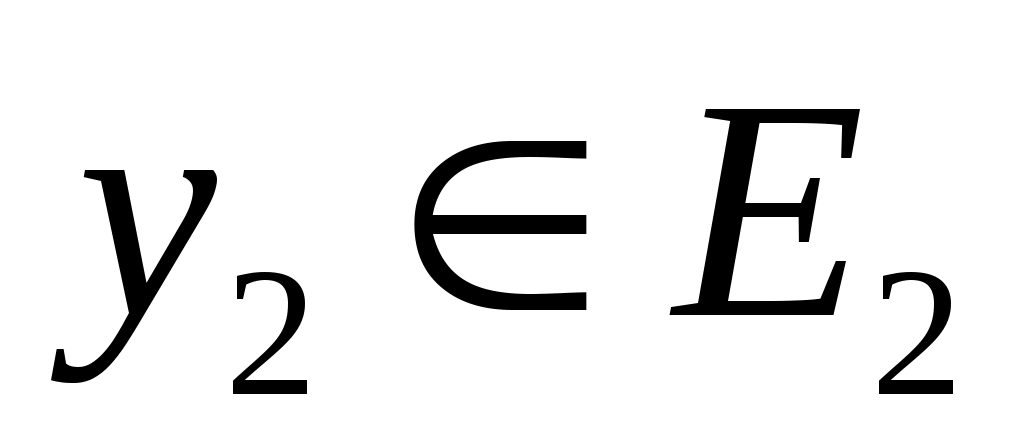 . Напишите
. Напишите 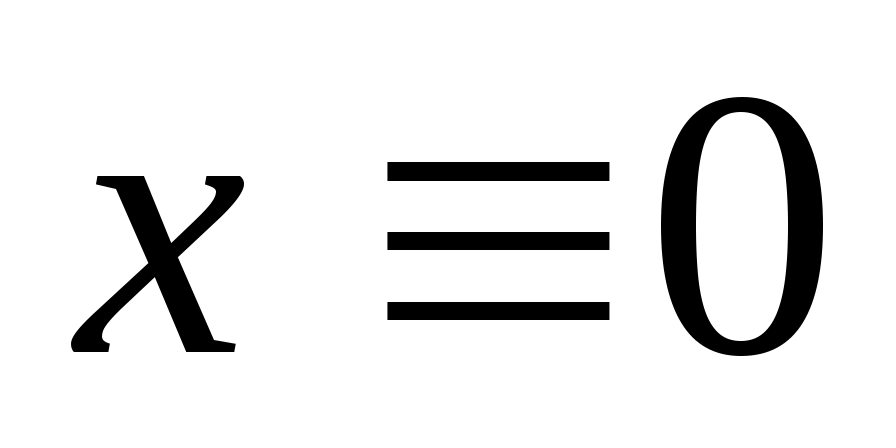
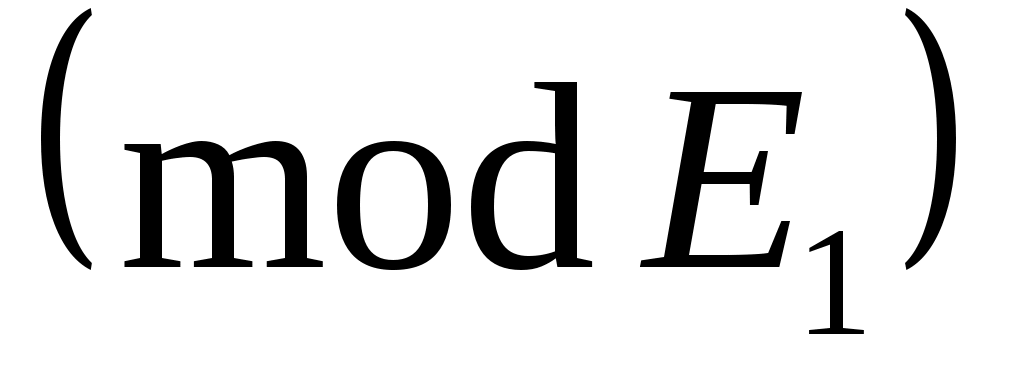 , если
, если 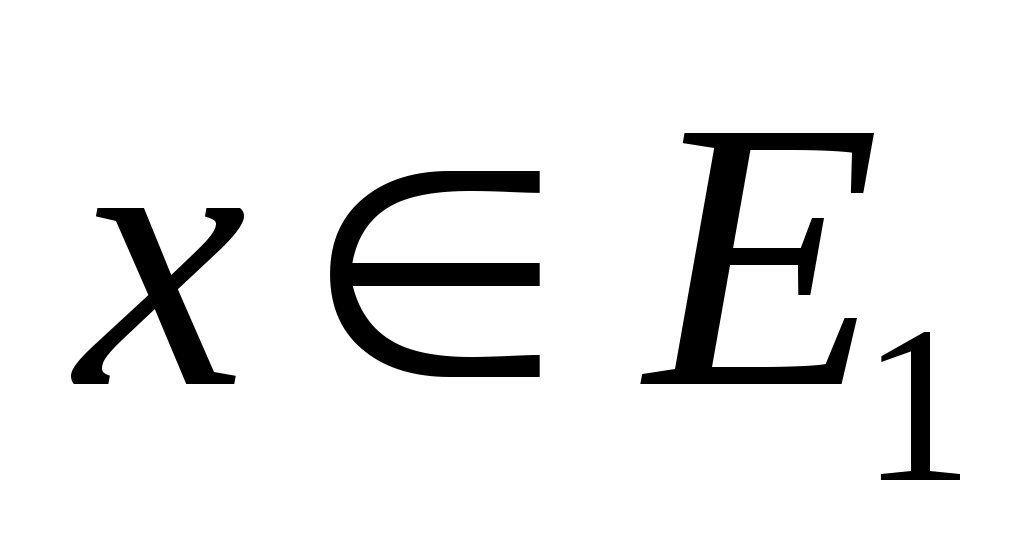 . Векторы
. Векторы 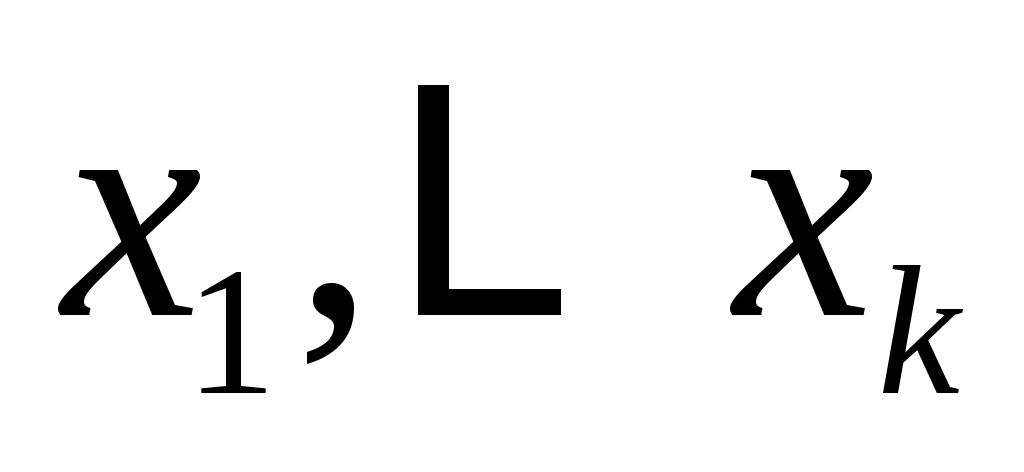 линейно независимы
линейно независимы 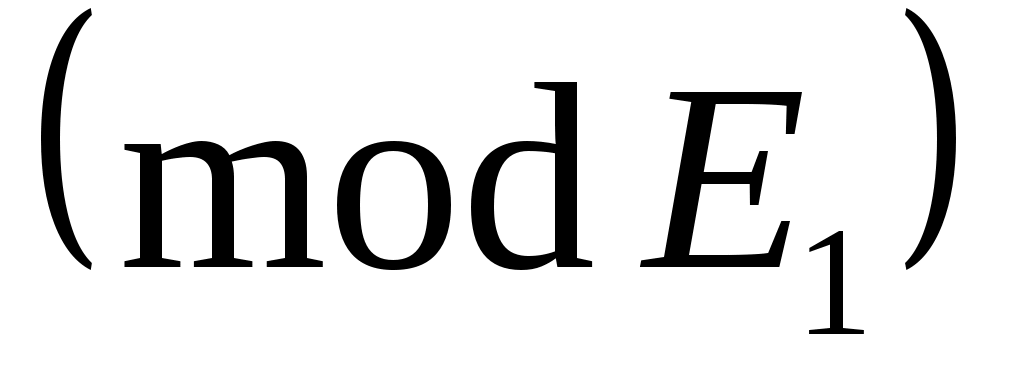 , если из соотношения
, если из соотношения 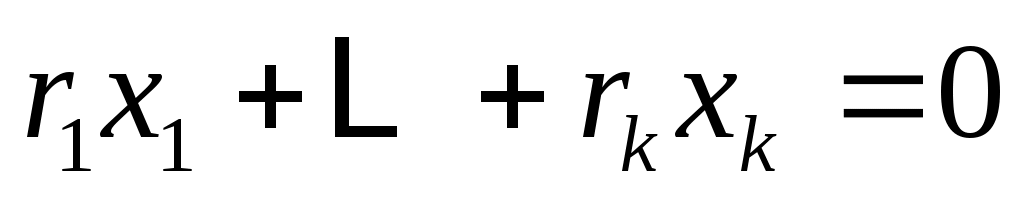
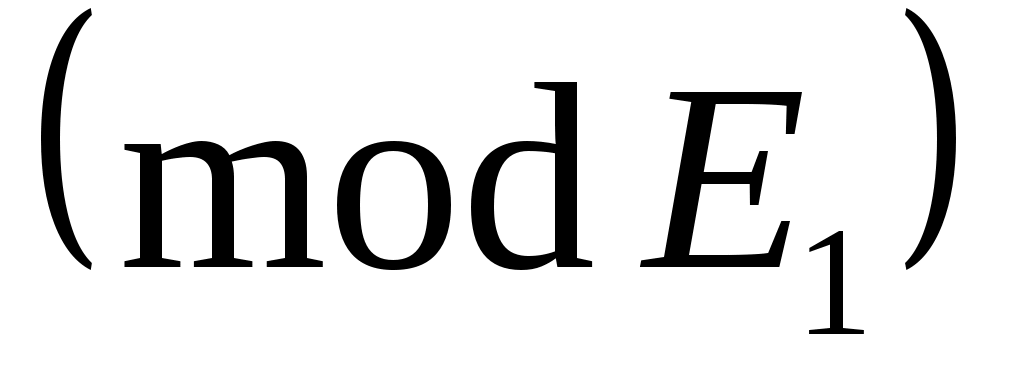 следует
следует 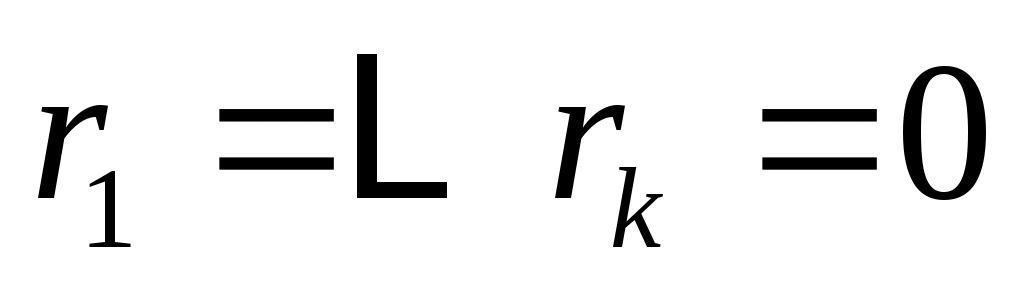 , для всех множеств скаляров
, для всех множеств скаляров 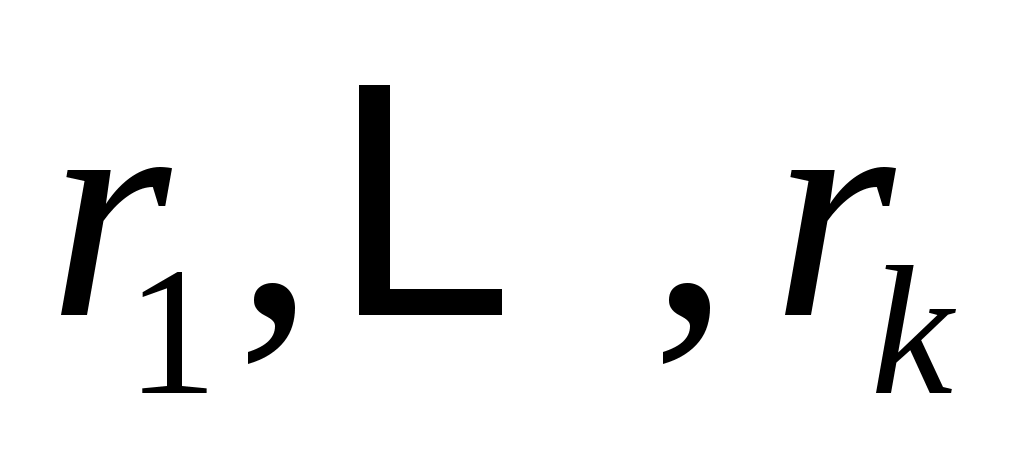 . Для некоторого
. Для некоторого 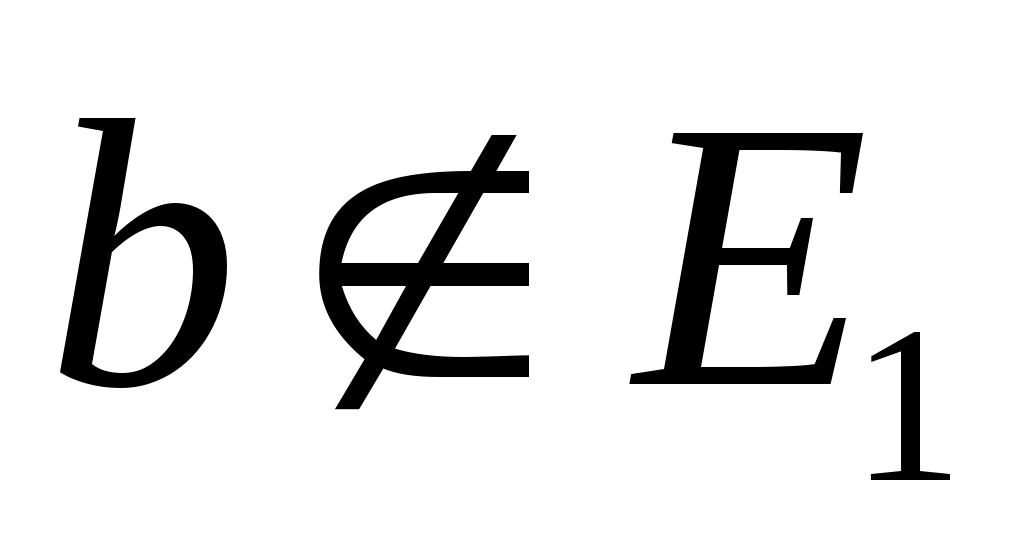
пусть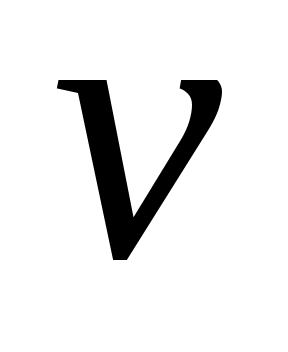 будет наибольшим целым числом таким, чтобы векторы
будет наибольшим целым числом таким, чтобы векторы
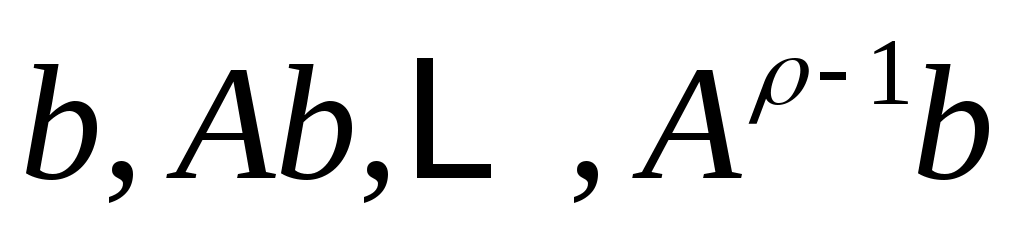
линейно независимы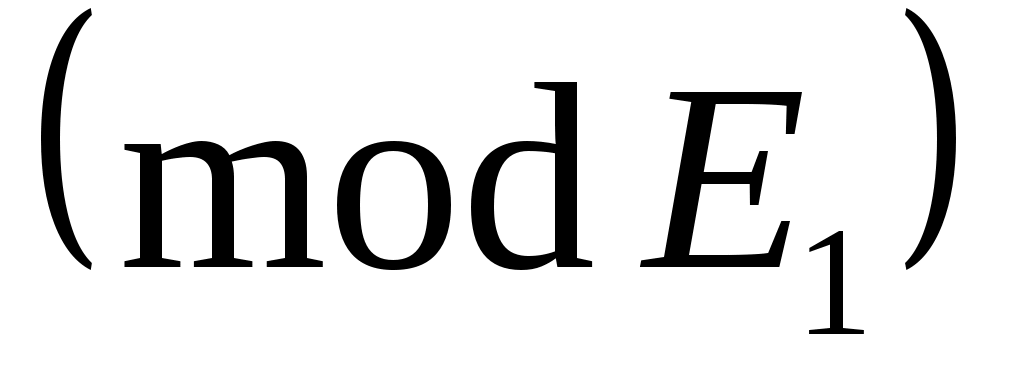 , и пусть
, и пусть 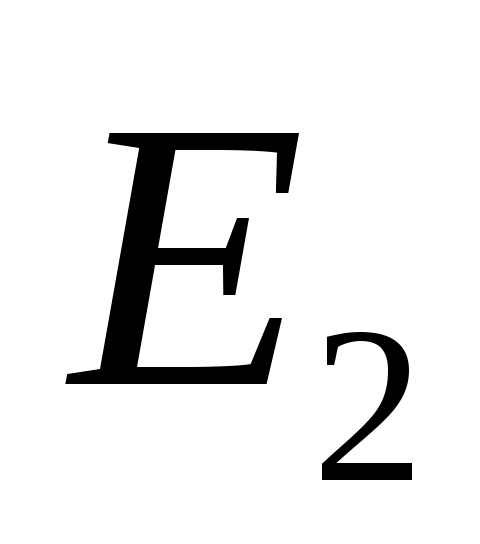 будет их пролетом. Тогда
будет их пролетом. Тогда 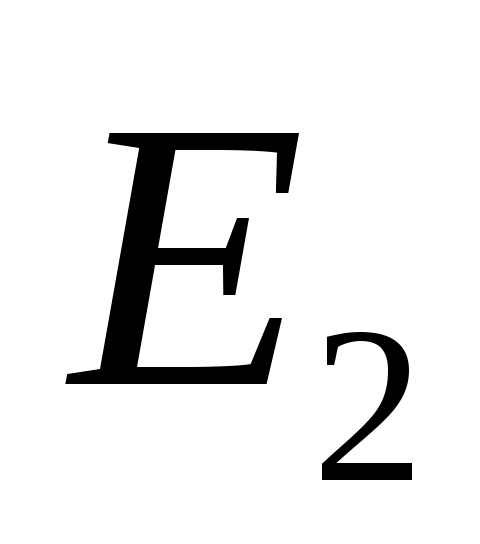 является циклическим
является циклическим 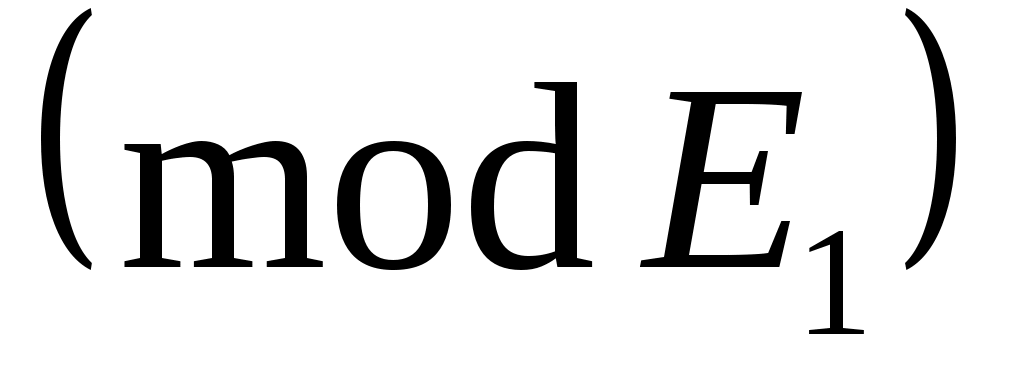 ; ясно, что
; ясно, что 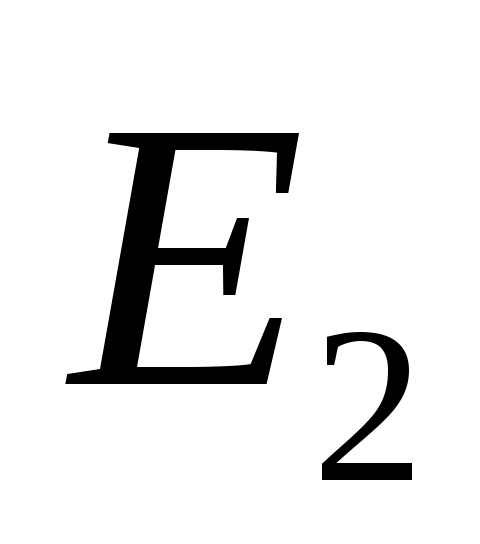 инвариантен
инвариантен 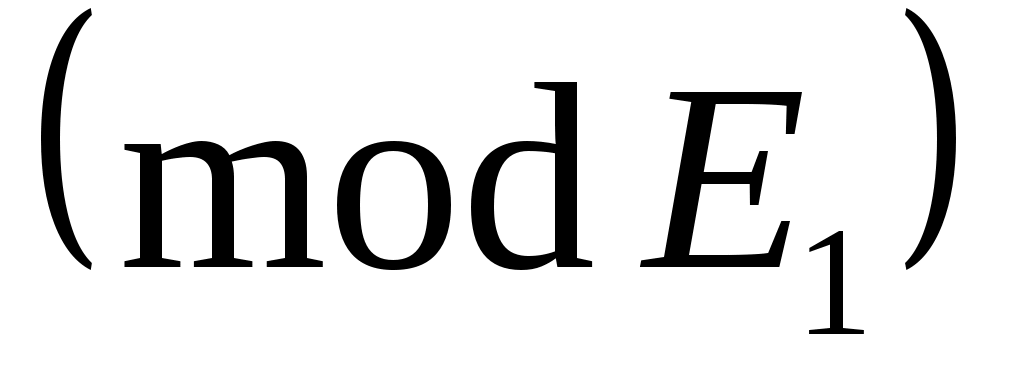 . Относительное минимальный полином для
. Относительное минимальный полином для 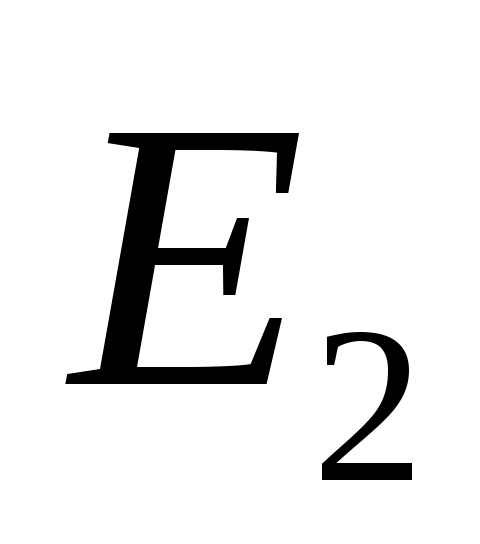
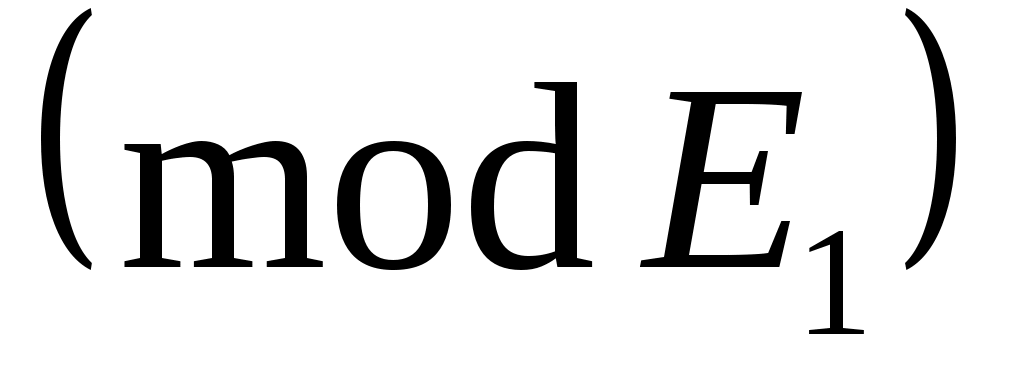 - это (уникальный) нормированный многочлен
- это (уникальный) нормированный многочлен 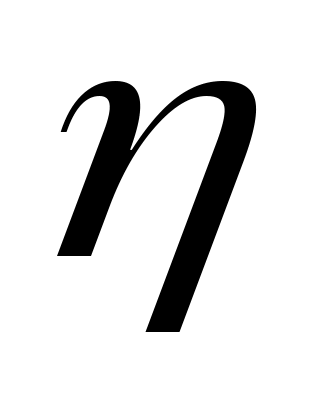 наименьшей степени такой, что
наименьшей степени такой, что 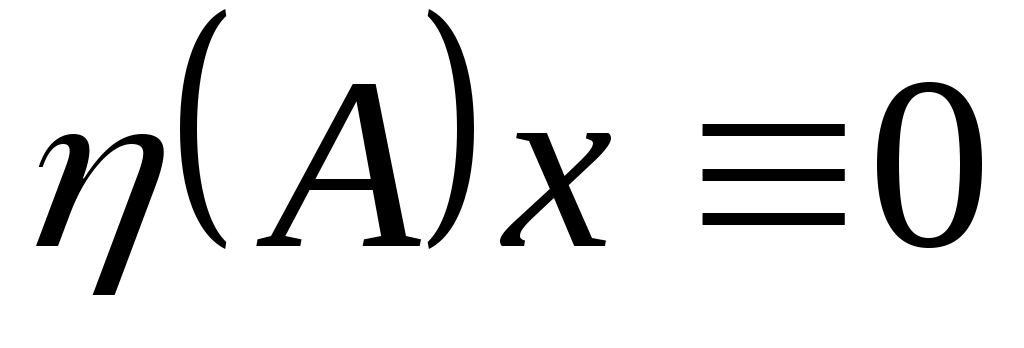
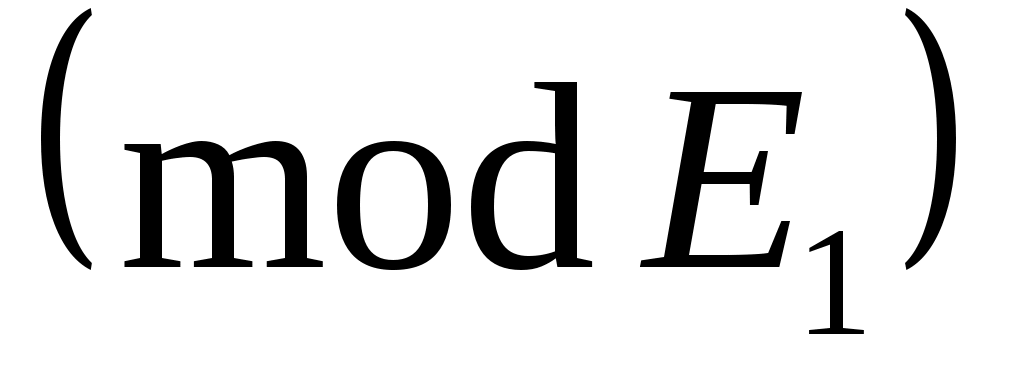 для всех
для всех 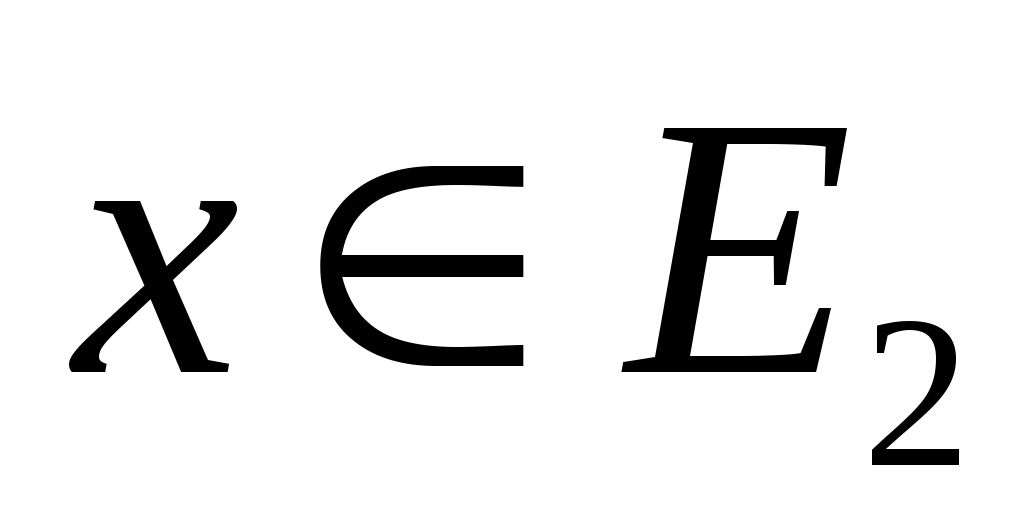 .
.
2) Доказательство необходимости: Теперь можно доказать необходимость. Пусть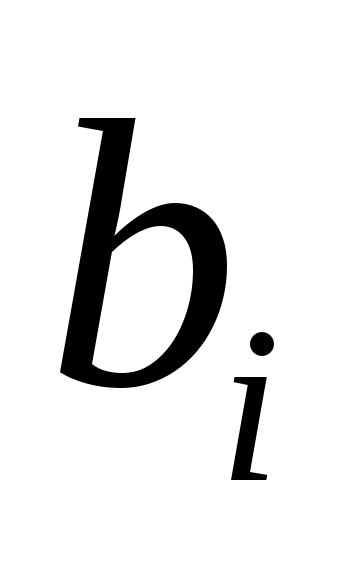 обозначает
обозначает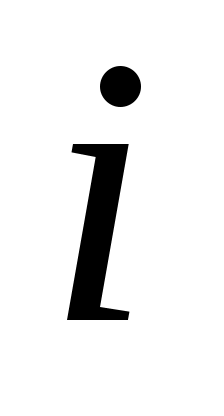 -й столбец
-й столбец 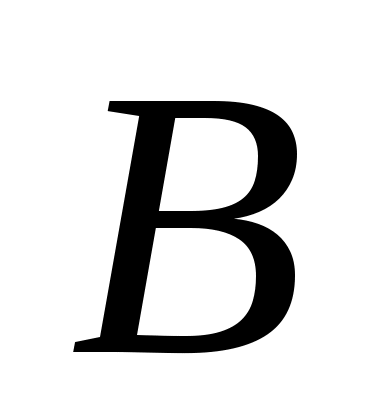 :
:
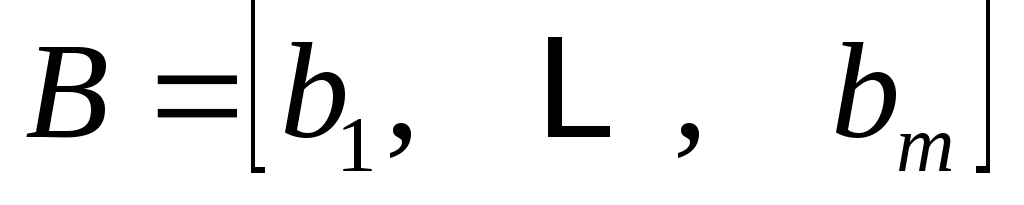 .
.
Пусть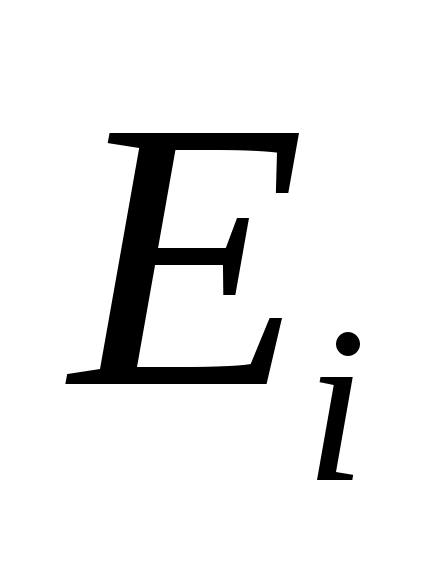 быть циклическим подпространством, порожденным
быть циклическим подпространством, порожденным 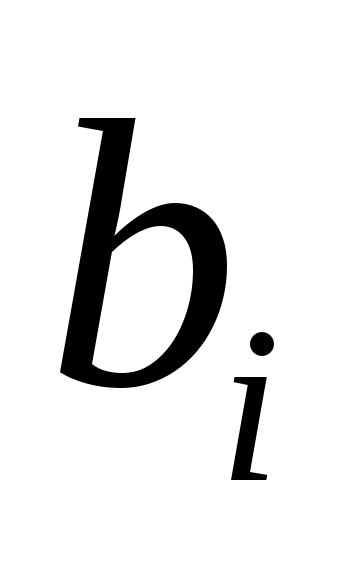 , и положить
, и положить 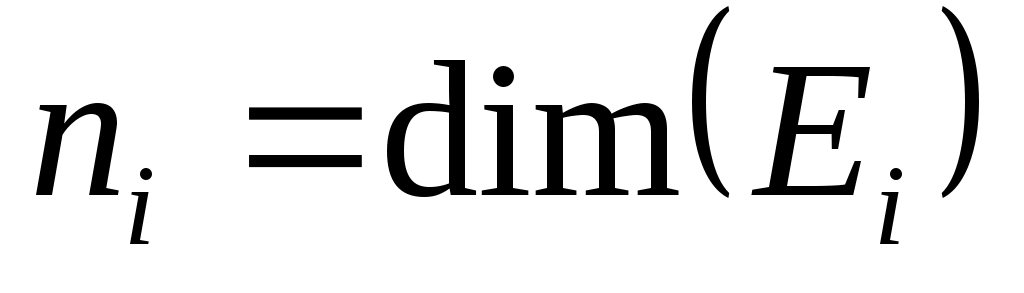 . Поскольку
. Поскольку 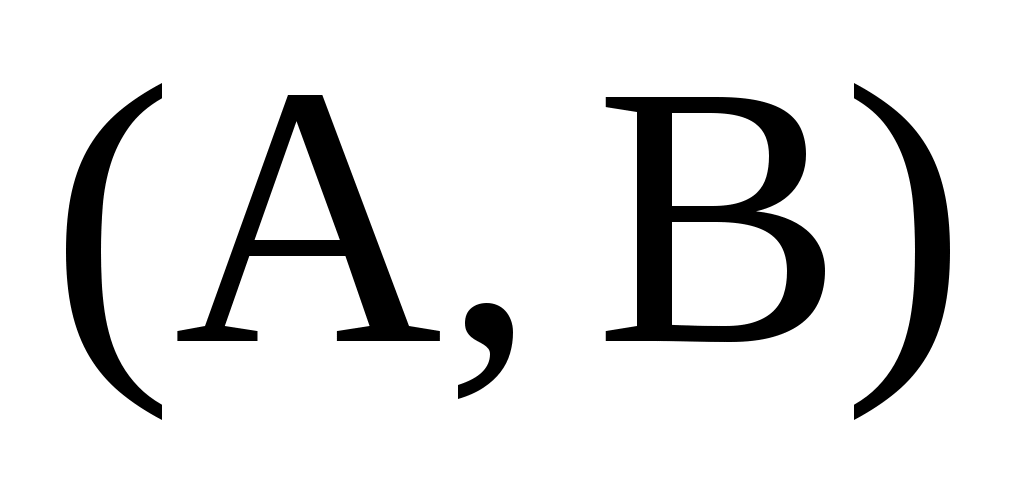 является управляемым,
является управляемым,
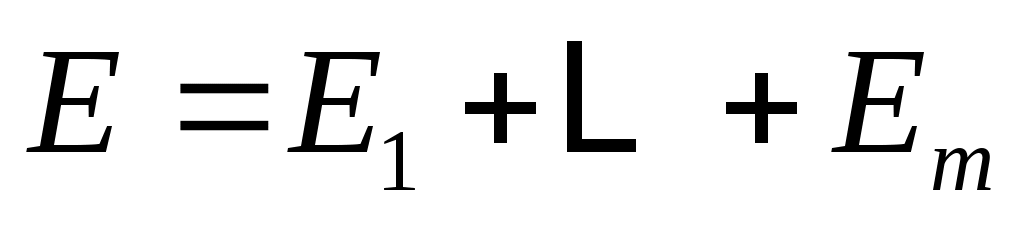
но в целом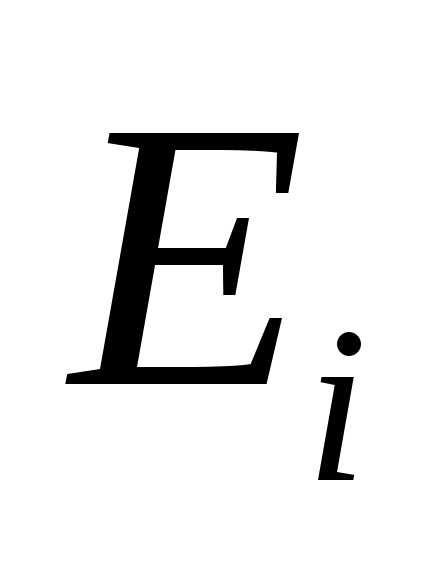 не являются независимыми. Тем не менее,
не являются независимыми. Тем не менее,  можно записать как прямую сумму
можно записать как прямую сумму
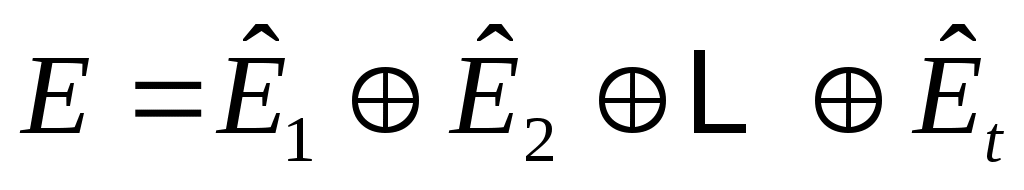 ,
, 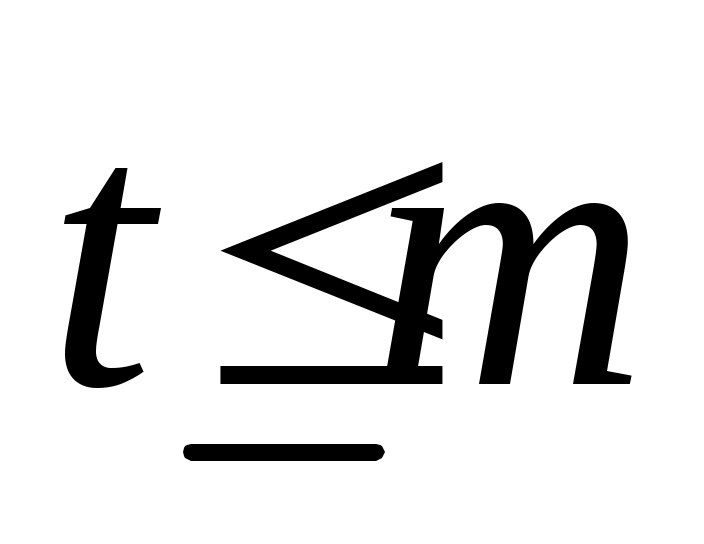 (6)
(6)
где определенные подпространства . Чтобы увидеть это, предположим, что
. Чтобы увидеть это, предположим, что 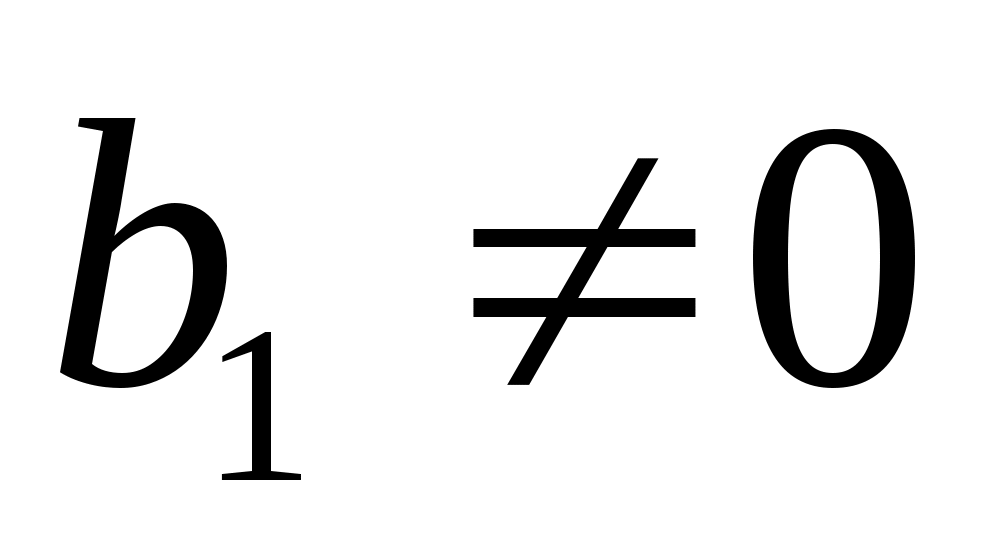 , и определим
, и определим 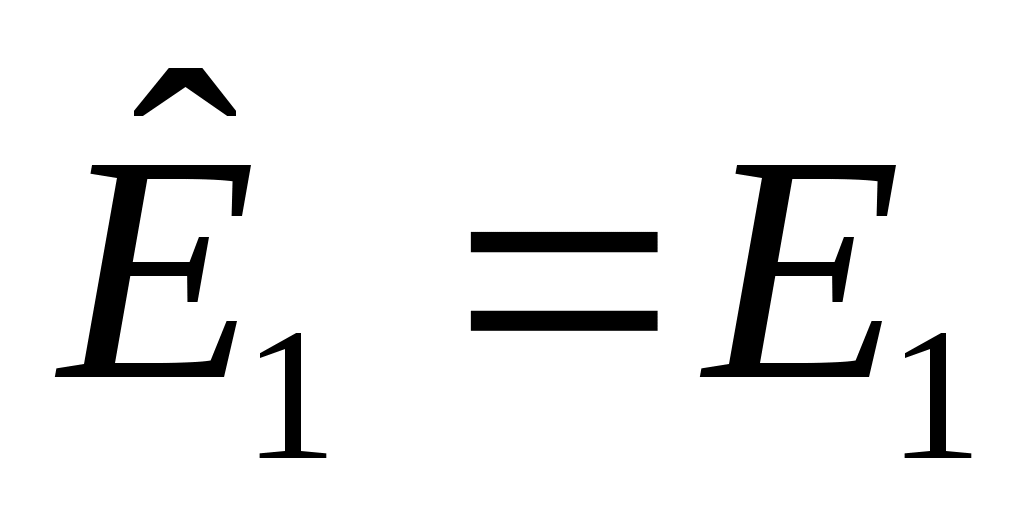 . Если
. Если 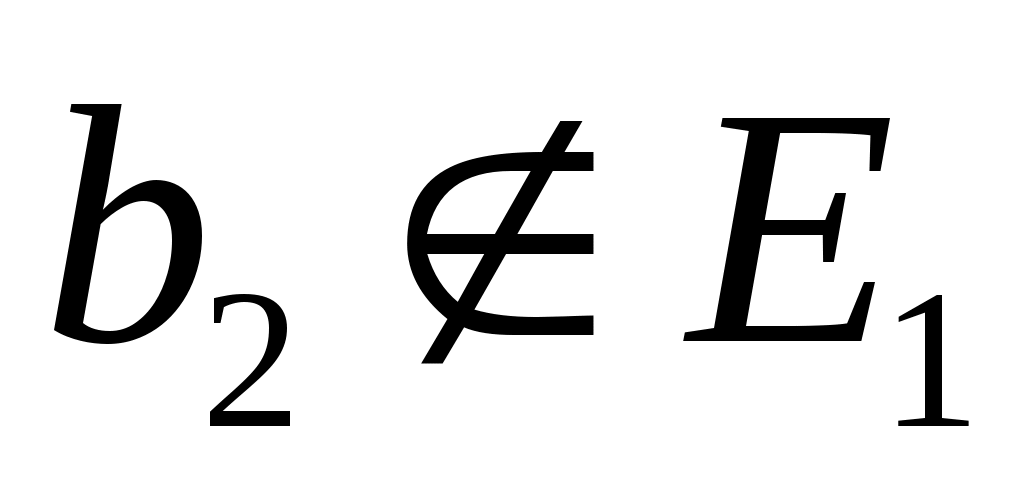 то пусть
то пусть 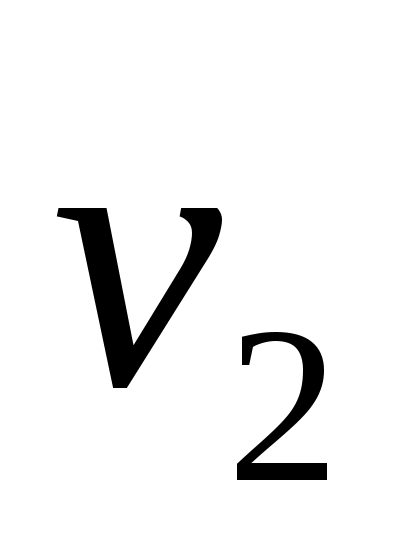 ,
, 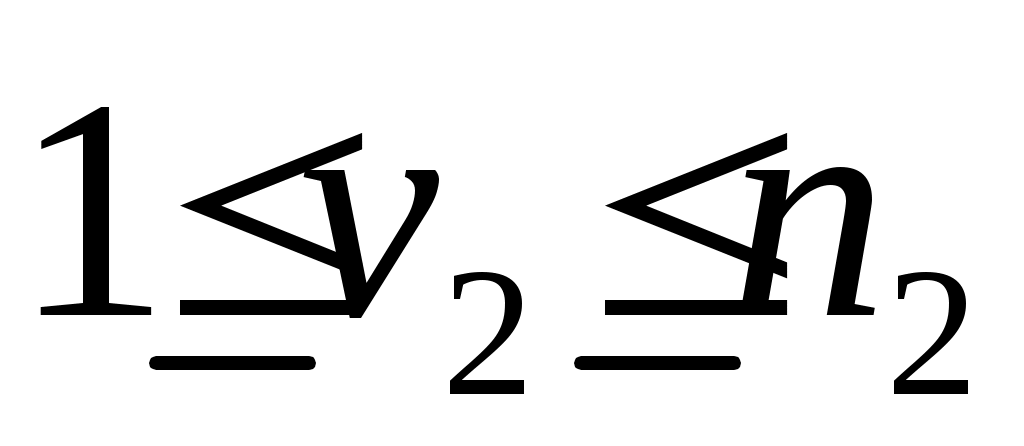 , будет наибольшим целым числом, таким, что векторы
, будет наибольшим целым числом, таким, что векторы
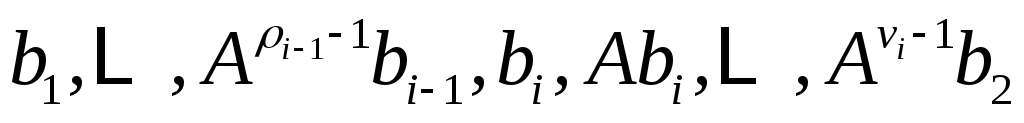
линейно независимы, и пусть будет пролетом
будет пролетом 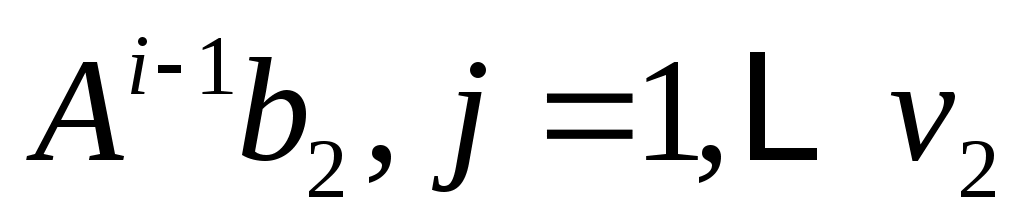 . Тогда
. Тогда 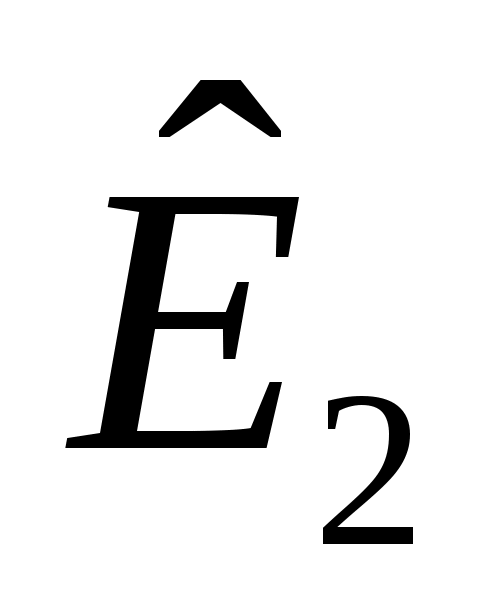 является циклическим
является циклическим 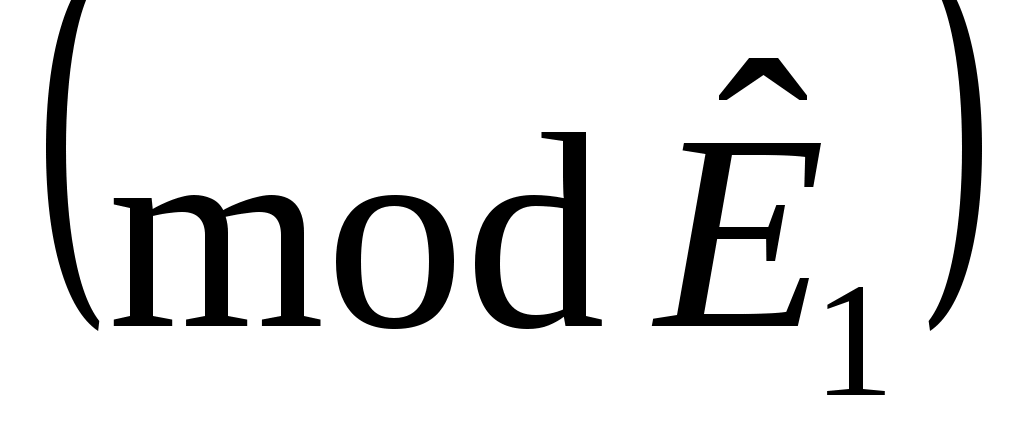 , с относительным минимальный полином степени
, с относительным минимальный полином степени 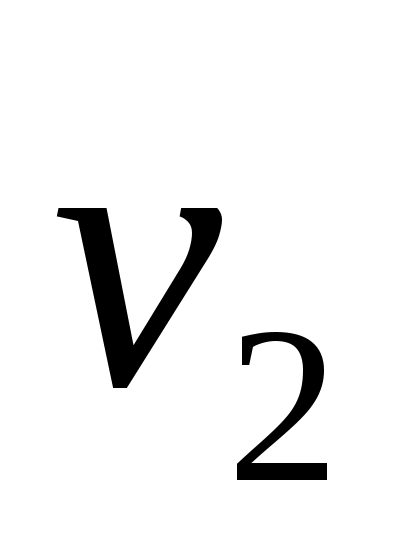 . Продолжая таким образом, для
. Продолжая таким образом, для 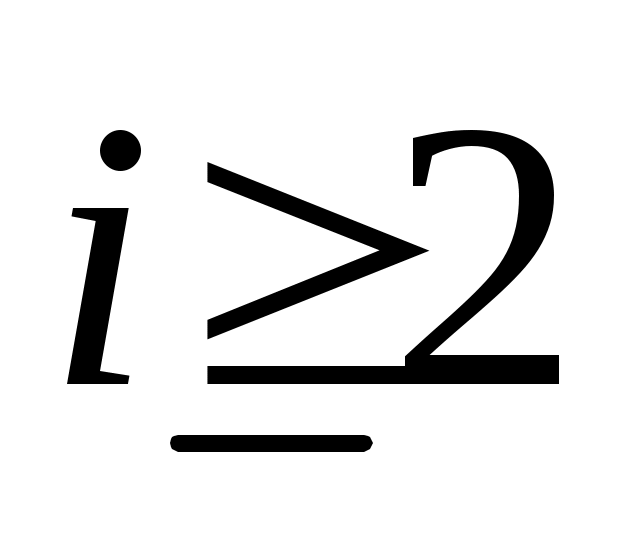 определим
определим 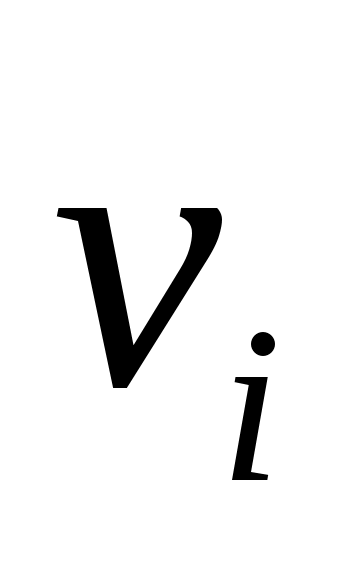 ,
, 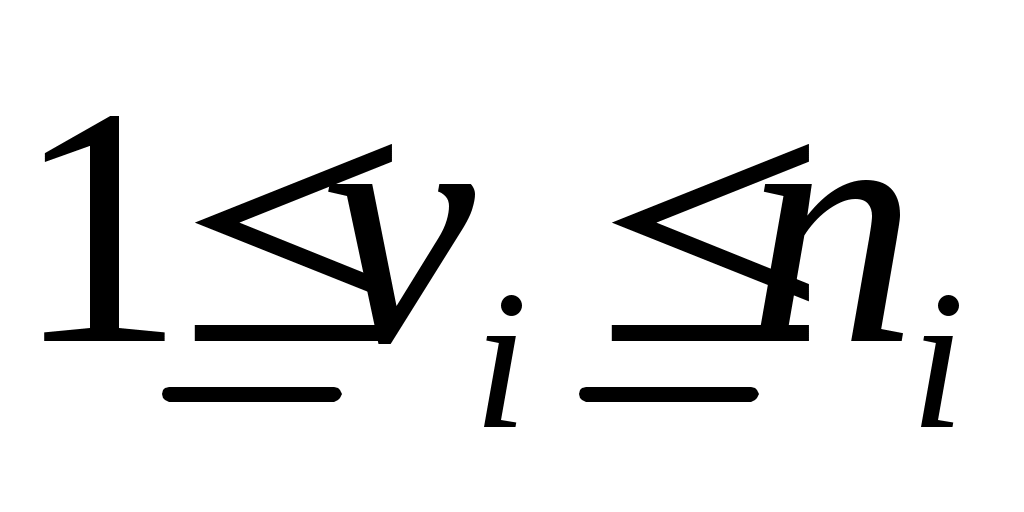 , чтобы быть наибольшим целым числом таким, чтобы векторы.
, чтобы быть наибольшим целым числом таким, чтобы векторы.
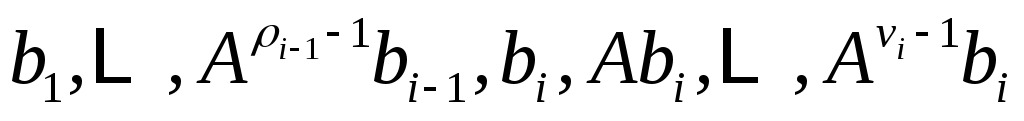
линейно независимы, и пусть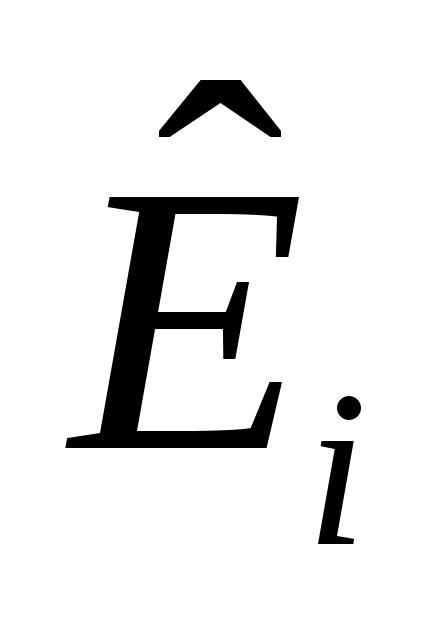 будет пролетом
будет пролетом 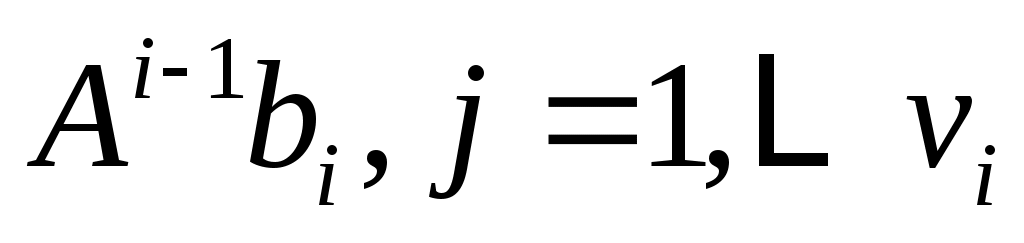 . Тогда
. Тогда
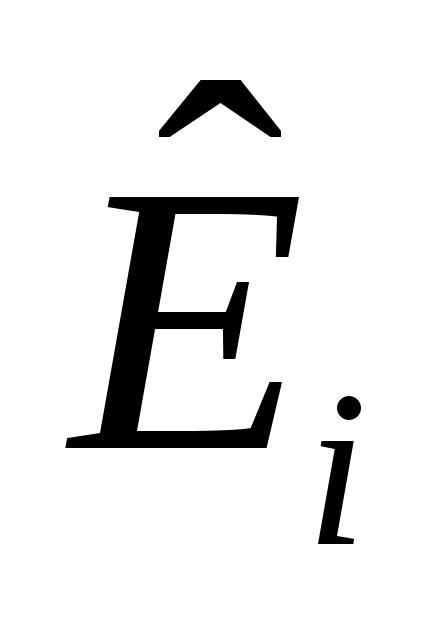 циклическое
циклическое 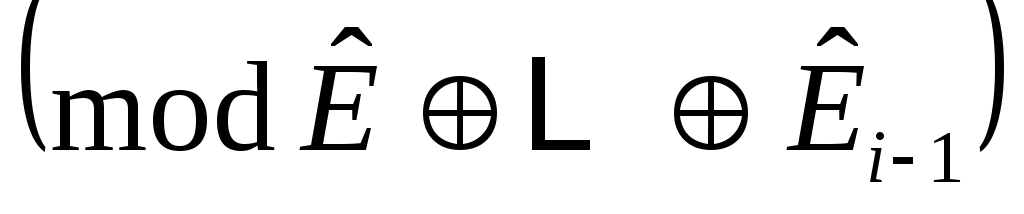 с относительным минимальный полином степени
с относительным минимальный полином степени 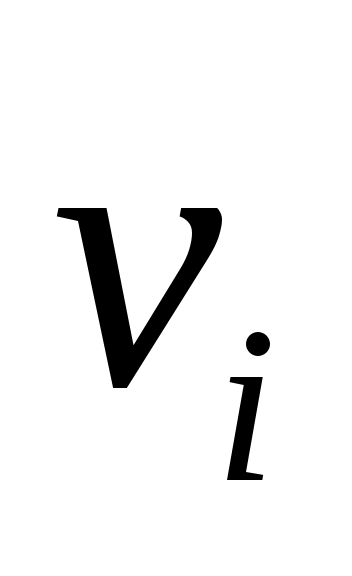 . Если на любом этапе
. Если на любом этапе 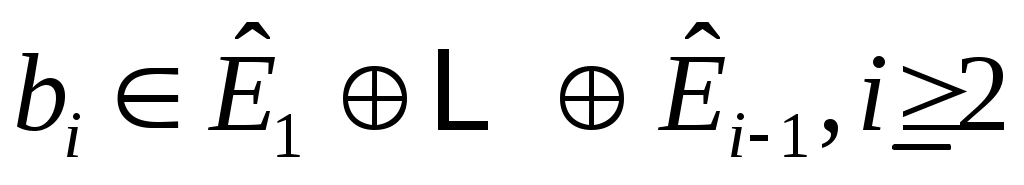 , то
, то 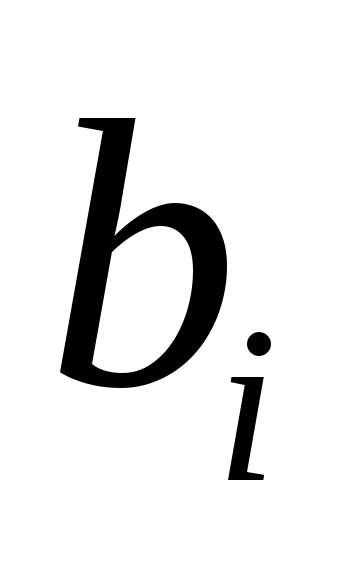 пропускается. Переупорядочив столбцы
пропускается. Переупорядочив столбцы 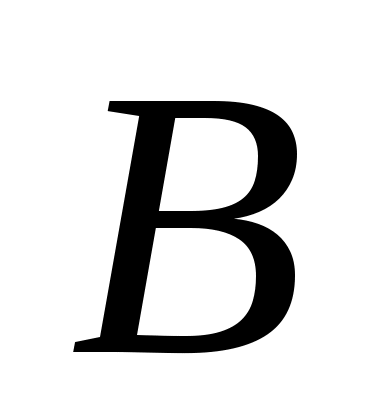 , если это необходимо, можно организовать, что для
, если это необходимо, можно организовать, что для 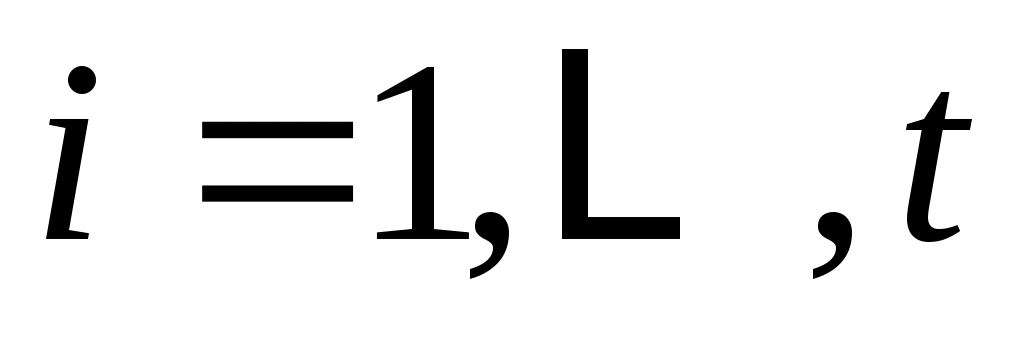 векторы
векторы 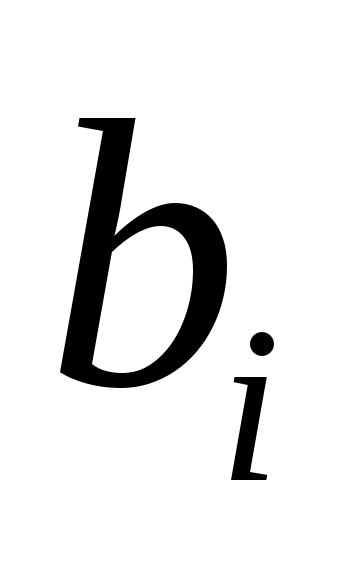 порождают независимые подпространства
порождают независимые подпространства 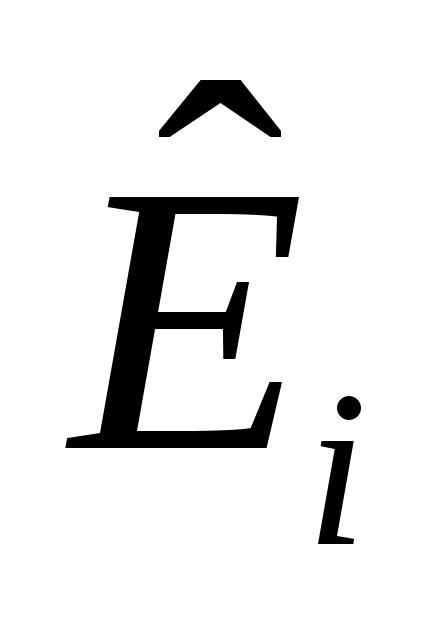 , где либо
, где либо 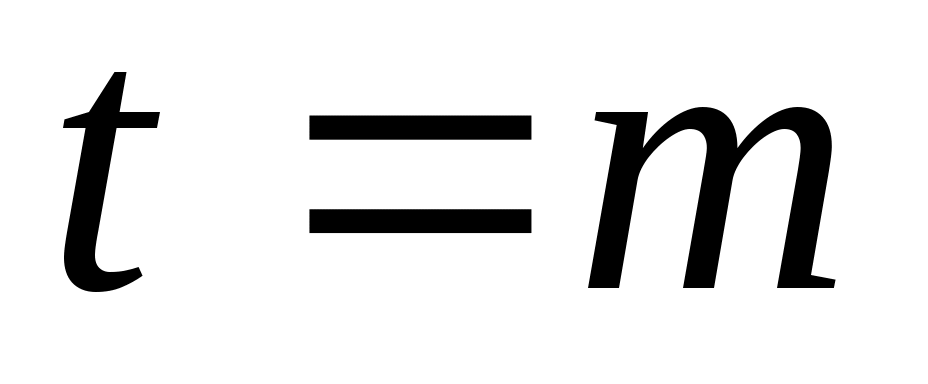 , либо
, либо 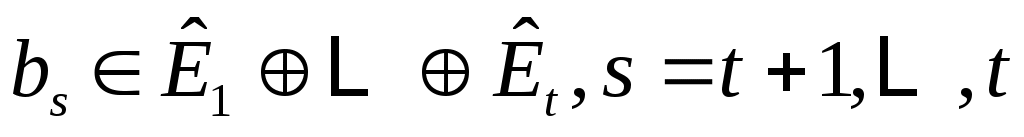 . Поскольку
. Поскольку 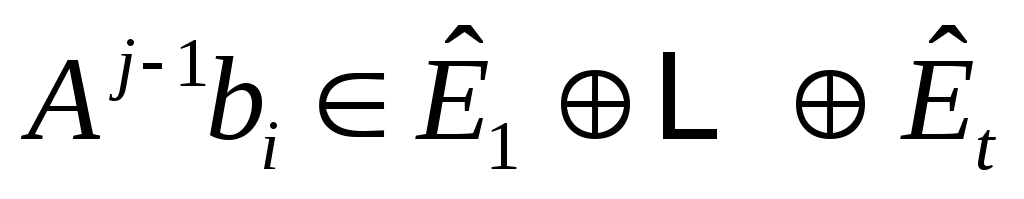 , если
, если 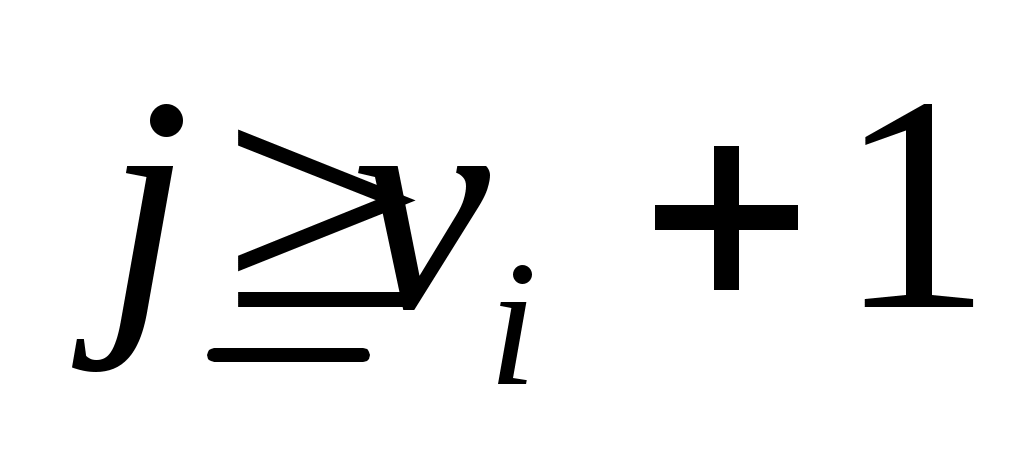 ,
, 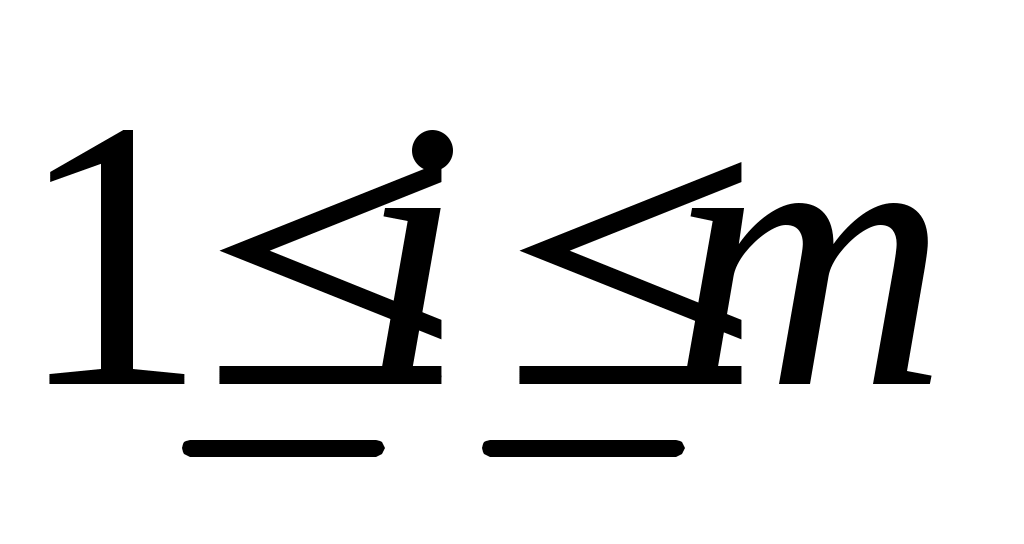 , то следует, что (6) верно и, следовательно,
, то следует, что (6) верно и, следовательно, 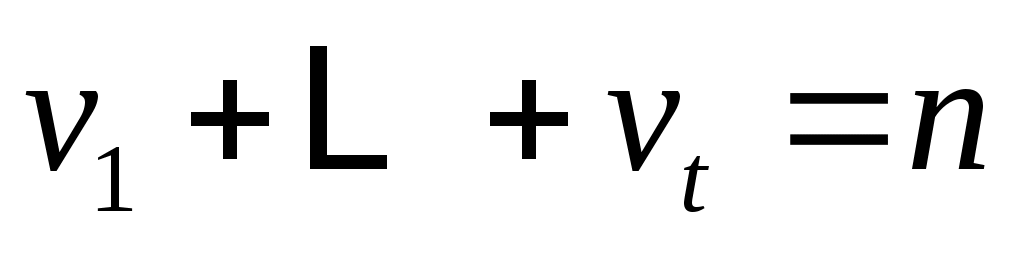 .
.
Далее трансформируется в удобную стандартную форму.
трансформируется в удобную стандартную форму.
Позволять
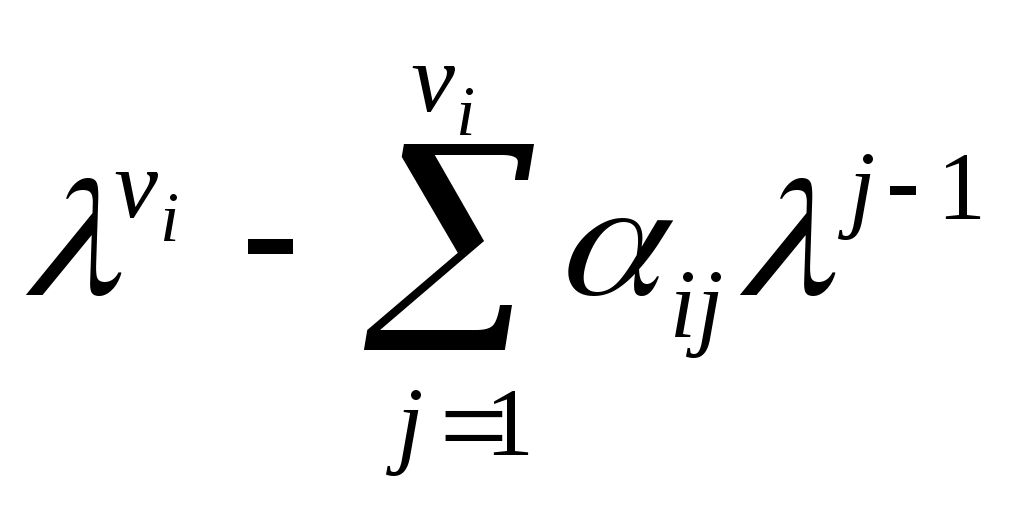 ,
, 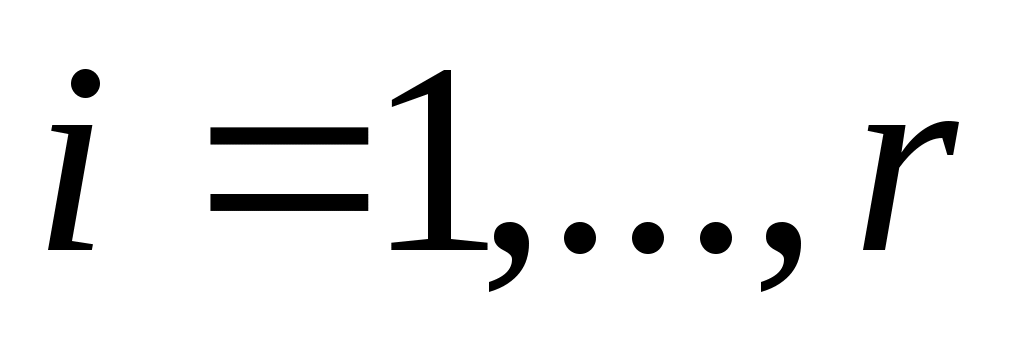 (7)
(7)
быть относительным минимальный полином для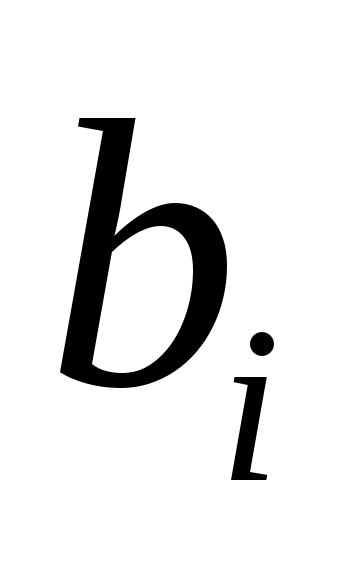
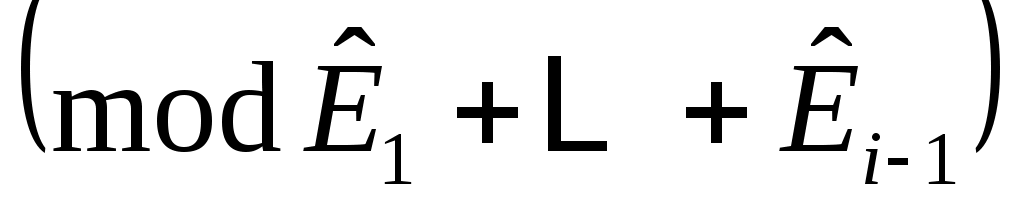 или абсолютным минимальный полином для
или абсолютным минимальный полином для 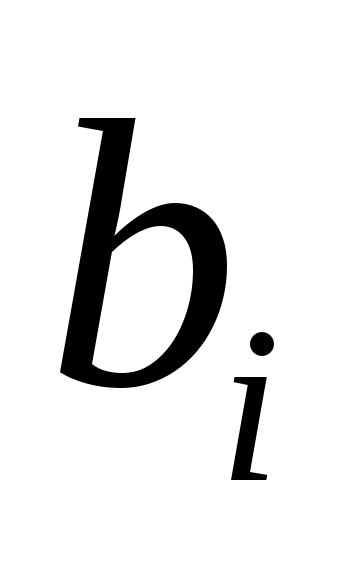 в случае
в случае 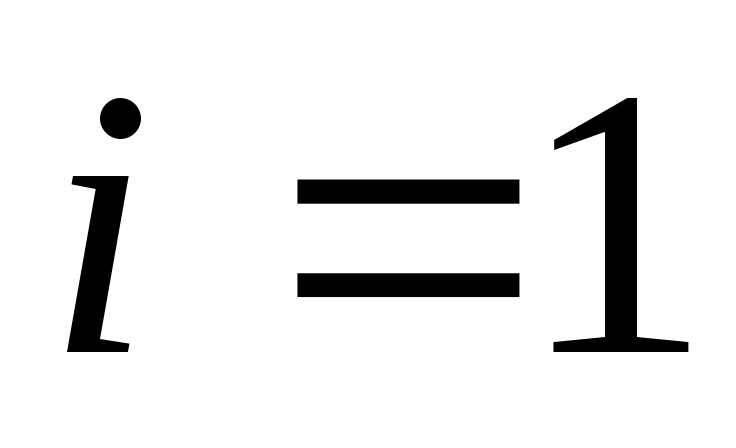 . Следуя Лангенхопу [2], ввести векторы
. Следуя Лангенхопу [2], ввести векторы
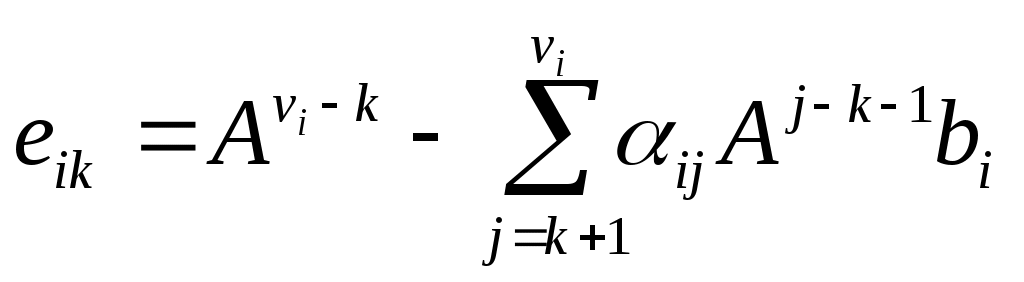
,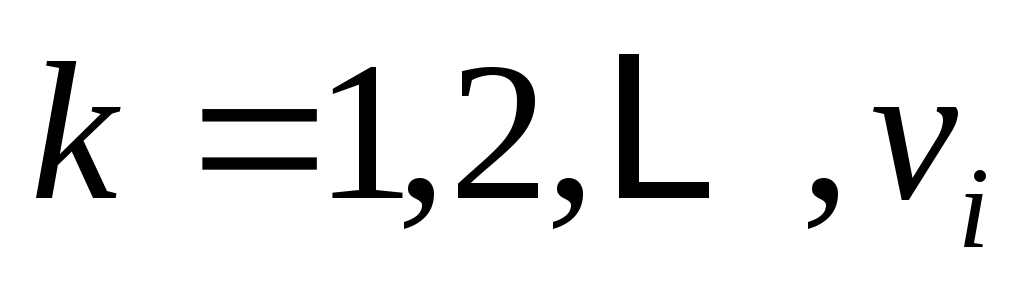 ,
, 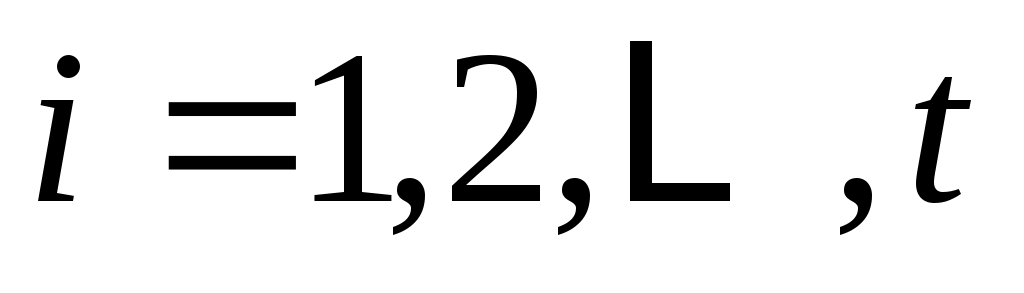 (8а)
(8а)
где суммирование не появляется в случае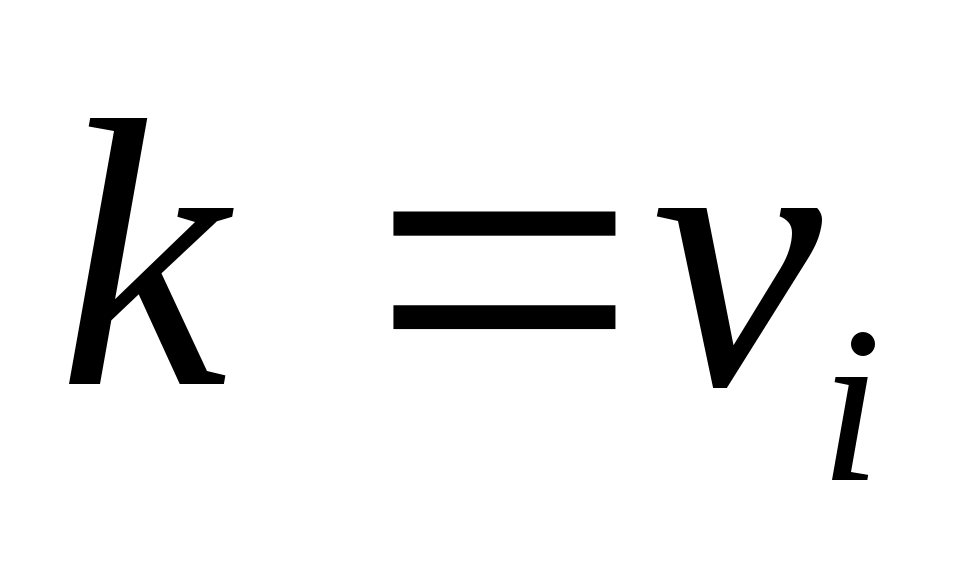 ; то есть,
; то есть,
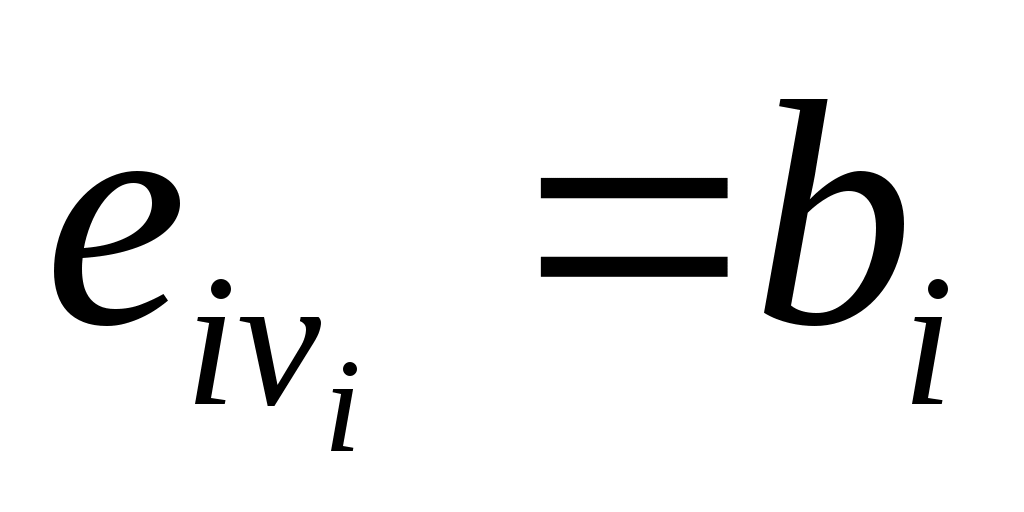 ,
, 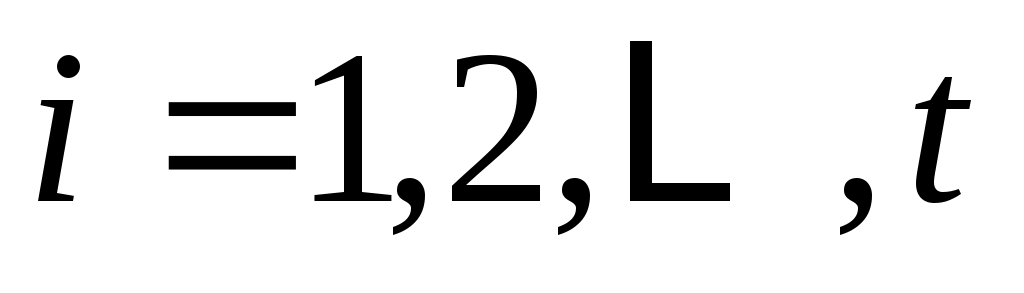 . (8b)
. (8b)
Понятно, что для каждого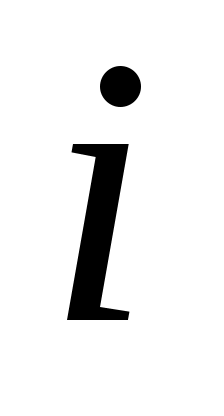 векторы
векторы 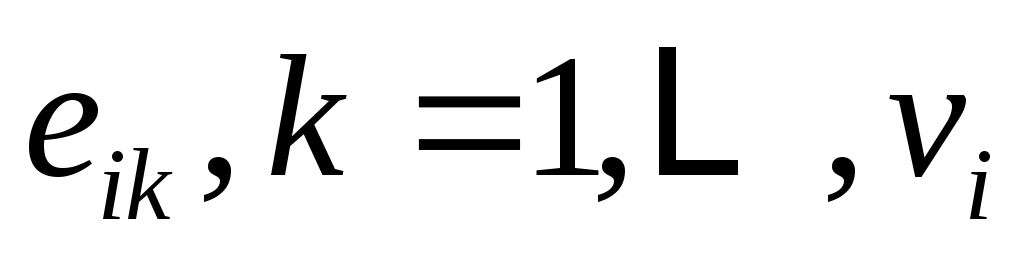 , являются независимыми линейными комбинациями векторов
, являются независимыми линейными комбинациями векторов 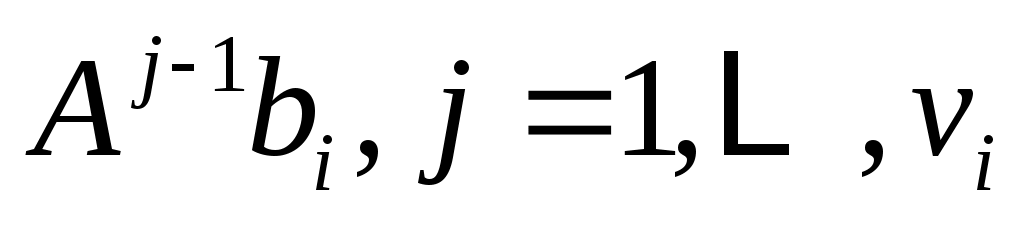 , и, следовательно, весь набор
, и, следовательно, весь набор 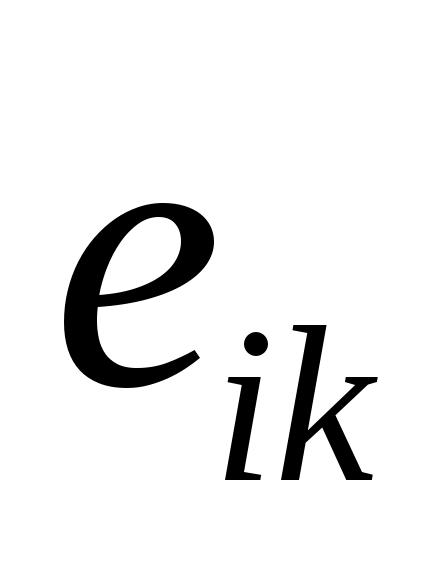 , является основой для
, является основой для  . Заметим, что для
. Заметим, что для 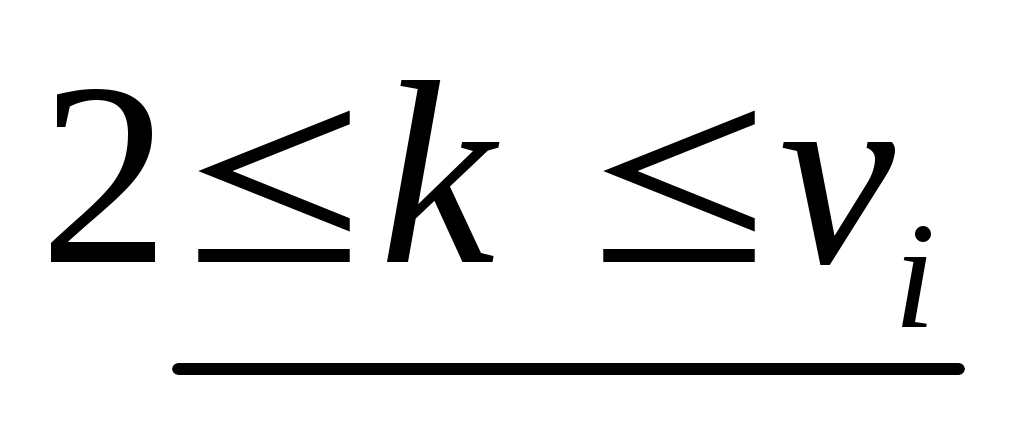
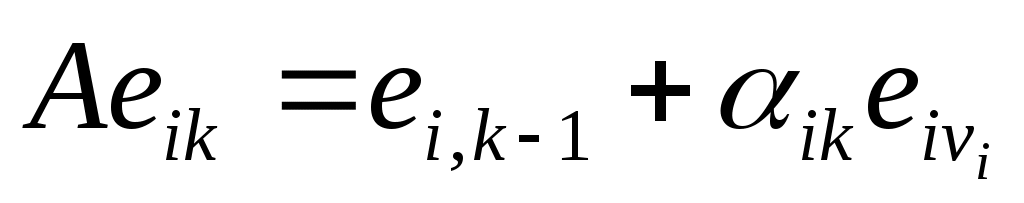 ,
, 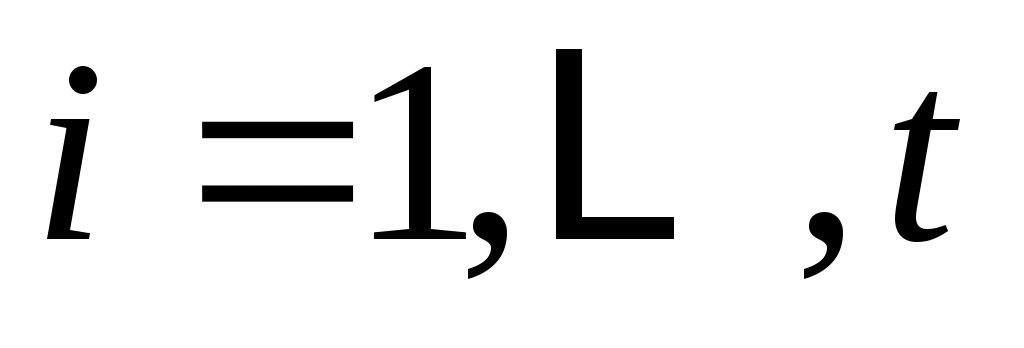 (9a)
(9a)
Кроме того, из-за того факта, что относительное минимальный полином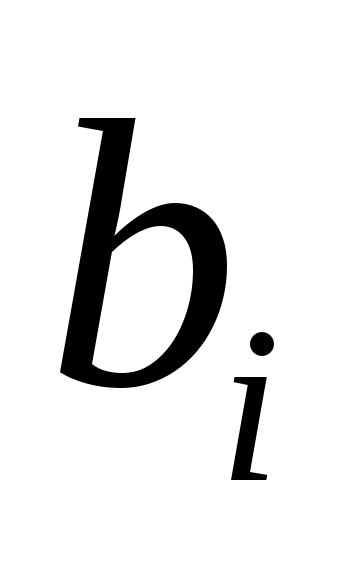
 имеет степень
имеет степень 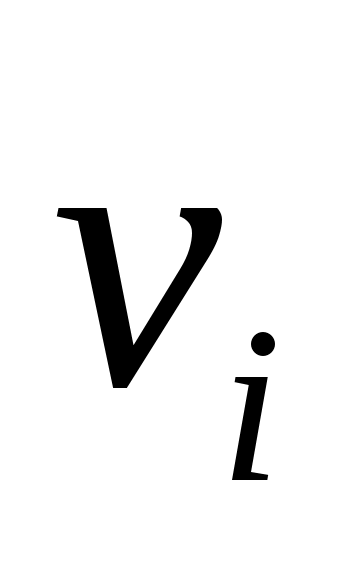 , следует (см. (7))
, следует (см. (7))
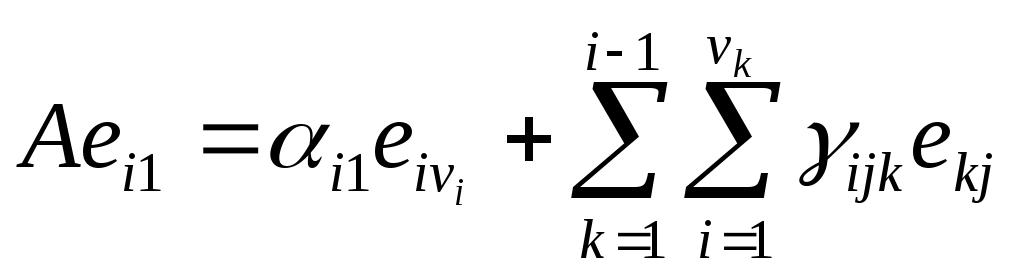 ,
, 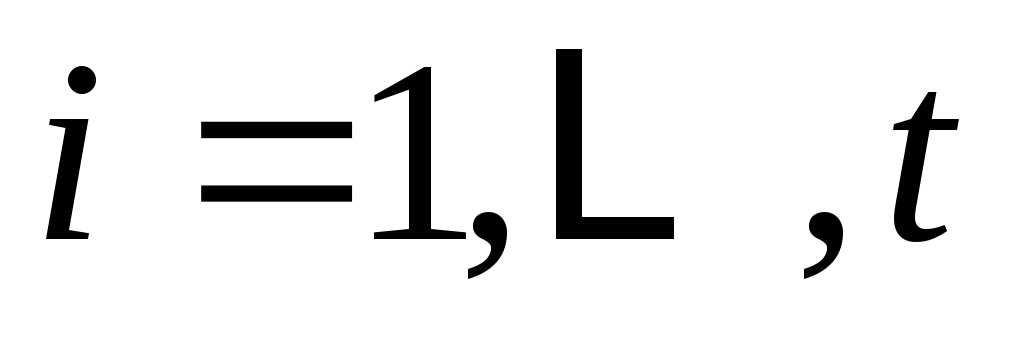 (9b)
(9b)
для некоторых скаляров , и где двойное суммирование не появляется, если
, и где двойное суммирование не появляется, если 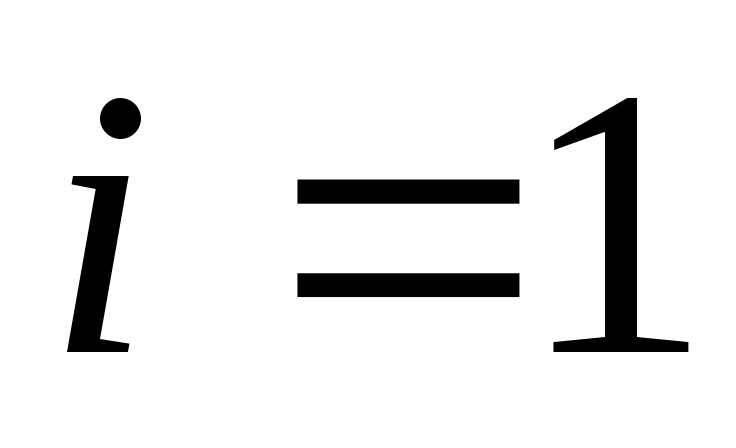 .
.
Затем, используя (9), вычислите форму , рассматриваемой как линейное преобразование в
, рассматриваемой как линейное преобразование в  , относительно базиса
, относительно базиса 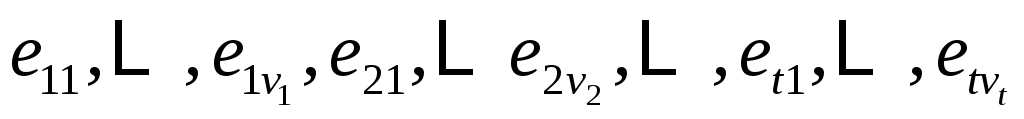
Следующее наблюдение будет полезно; простое доказательство опущено.
ЛЕММА 4: Если
Также используется концепция соответствия. Пусть
пусть
линейно независимы
2) Доказательство необходимости: Теперь можно доказать необходимость. Пусть
Пусть
но в целом
где определенные подпространства
линейно независимы, и пусть
линейно независимы, и пусть
Далее
Позволять
быть относительным минимальный полином для
,
где суммирование не появляется в случае
Понятно, что для каждого
Кроме того, из-за того факта, что относительное минимальный полином
для некоторых скаляров
Затем, используя (9), вычислите форму


