Файл: О назначении полюсов в многовходных управляемых линейных системах.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.03.2024
Просмотров: 26
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
имеет степень 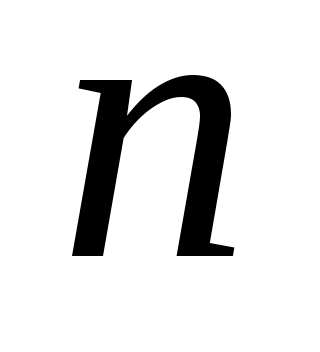 . Минимальный полином из
. Минимальный полином из  , как обычно, (уникальный) нормированный многочлен
, как обычно, (уникальный) нормированный многочлен 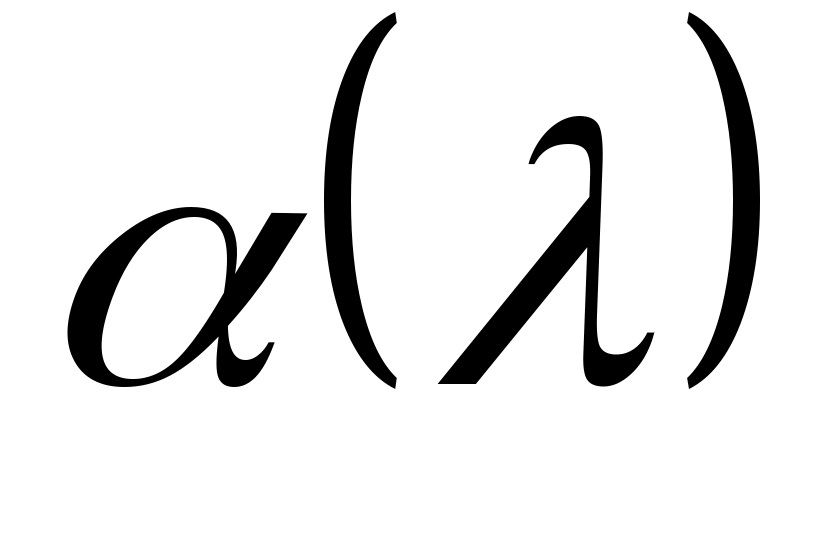 наименьшей степени такой, что
наименьшей степени такой, что 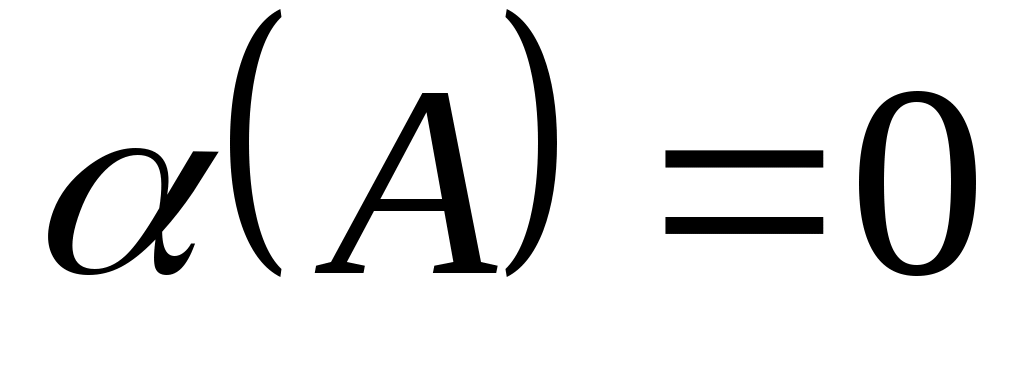 ;
; 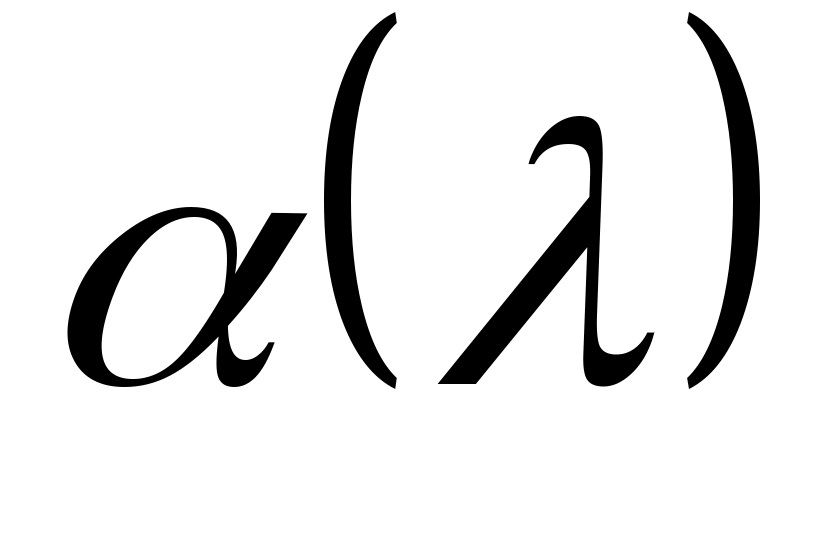 является наименьшим общим кратным минимальный полином
является наименьшим общим кратным минимальный полином 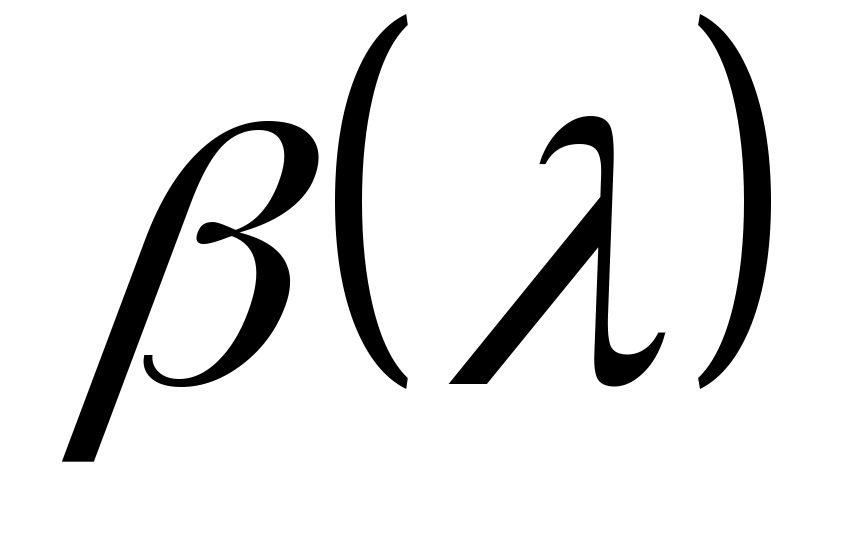 векторов
векторов 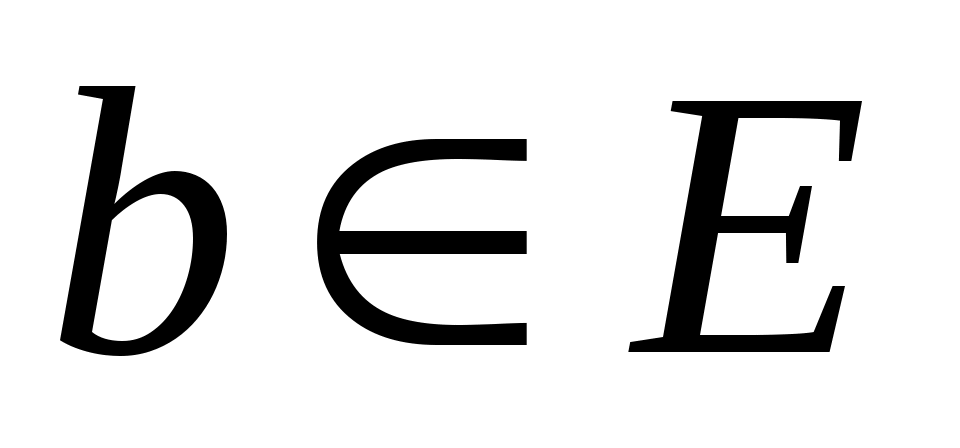 . Очевидно,
. Очевидно,  является циклическим, только если степень
является циклическим, только если степень 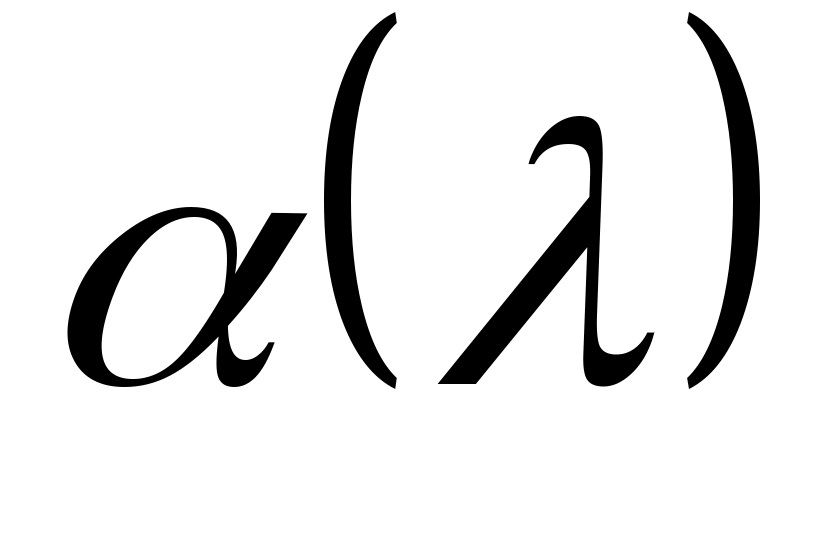 равна
равна 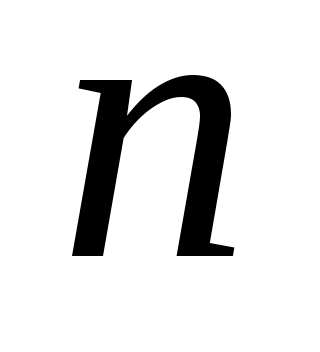 . Обратное утверждение можно сформулировать следующим образом.
. Обратное утверждение можно сформулировать следующим образом.
ЛЕММА 1: если минимальныйполином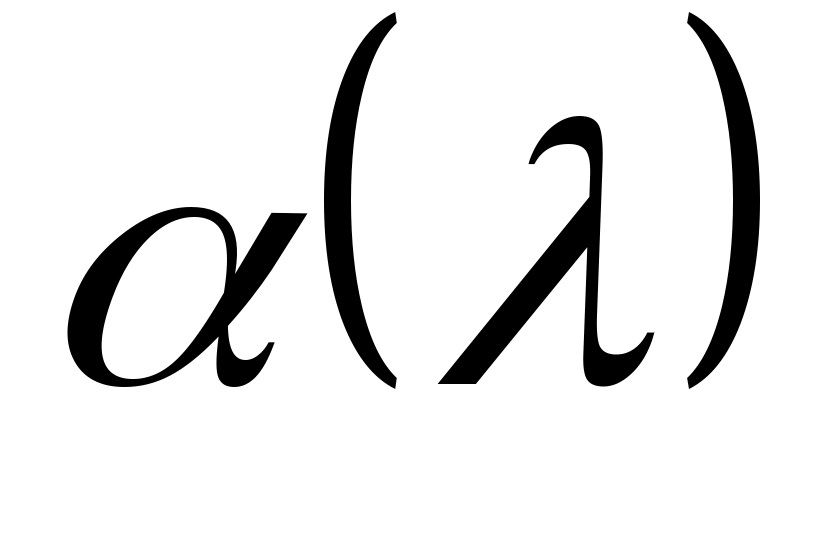 из
из  имеет степень
имеет степень 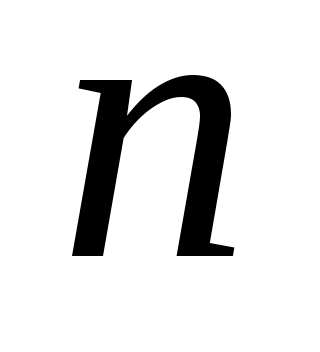 , то
, то  циклический, то есть существует
циклический, то есть существует 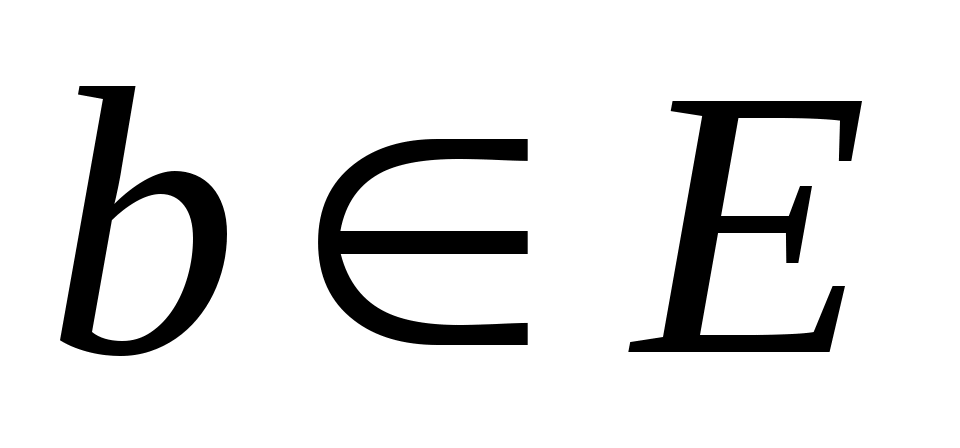 , такой что минимальный полином из
, такой что минимальный полином из 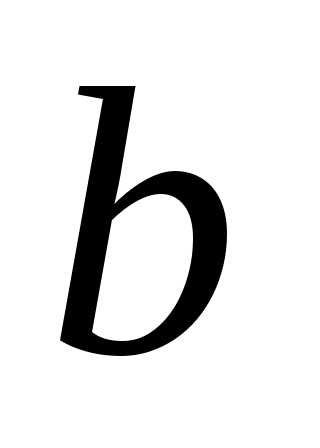 является
является 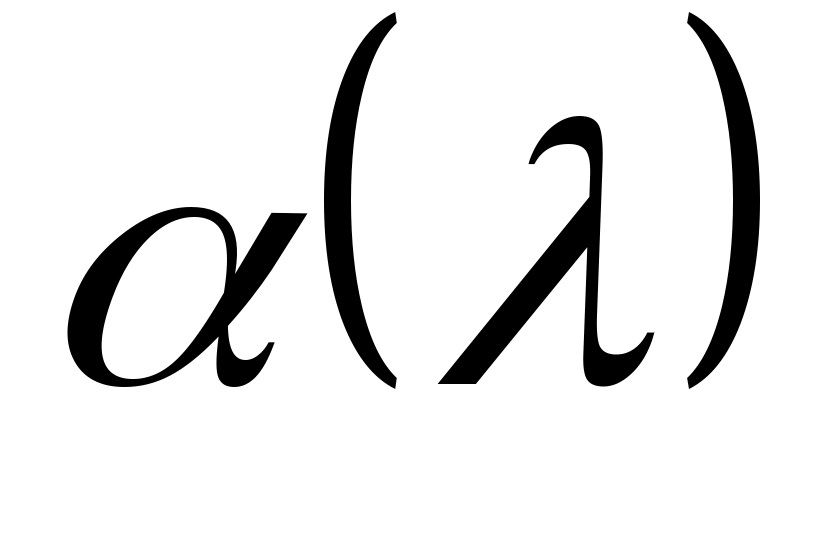 .
.
В частности, условие леммы 1 выполняется, если собственные значения различны.
различны.
Два нормированных полинома ,
, 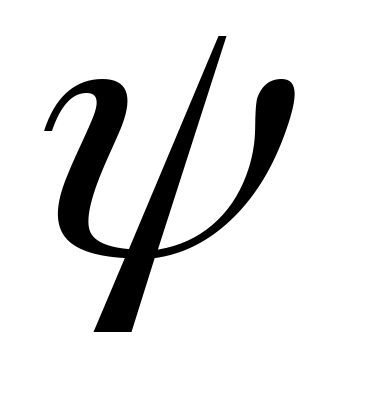 взаимно просты, если их наибольший общий делитель равен 1. Тогда [4] существуют такие полиномы
взаимно просты, если их наибольший общий делитель равен 1. Тогда [4] существуют такие полиномы 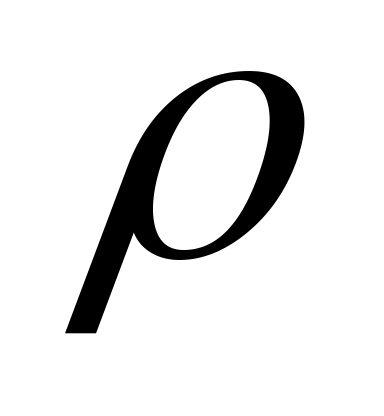 и
и 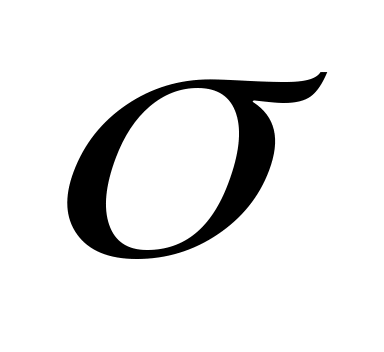
, что
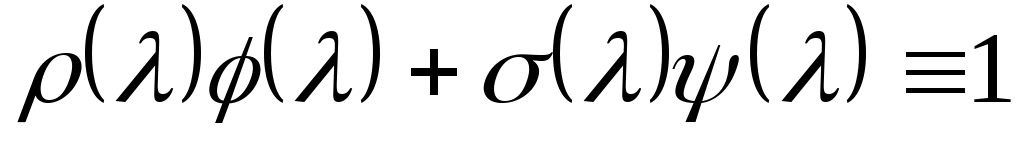
ЛЕММА 2: Пусть циклический, с минимальными полиномами
циклический, с минимальными полиномами  , и
, и 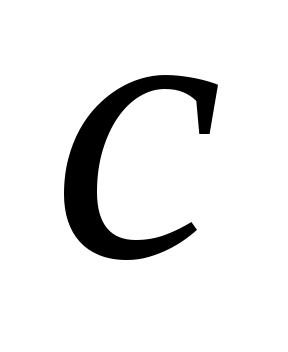 является генератором
является генератором  [4]. Если
[4]. Если 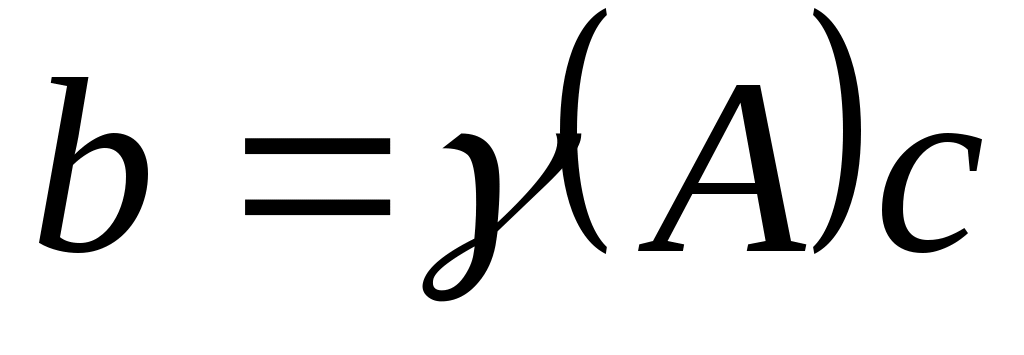 для некоторого полинома
для некоторого полинома 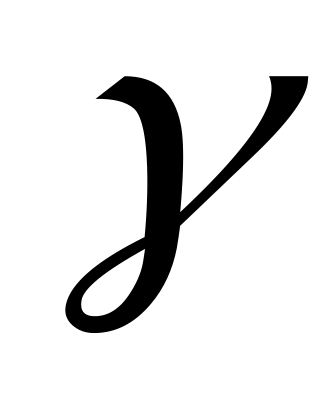 и если
и если  и
и 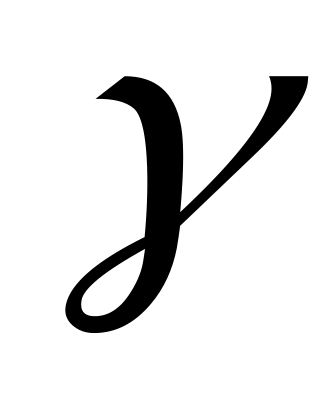 взаимно просты, то
взаимно просты, то 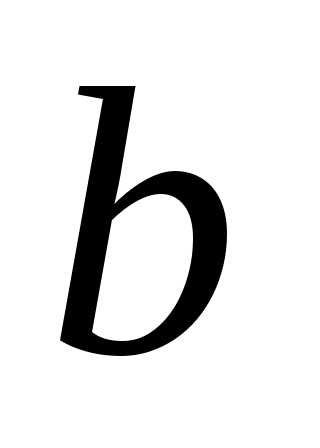 также является генератором
также является генератором  .
.
Обратное тоже верно, но не нужно.
Доказательство: Пусть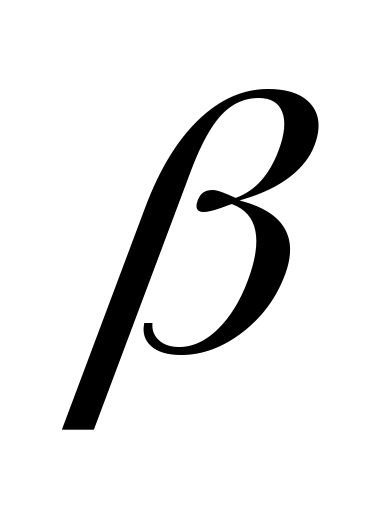 будет минимальный полином от
будет минимальный полином от 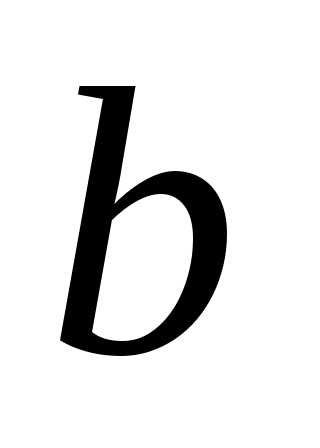 . Поскольку
. Поскольку  и
и 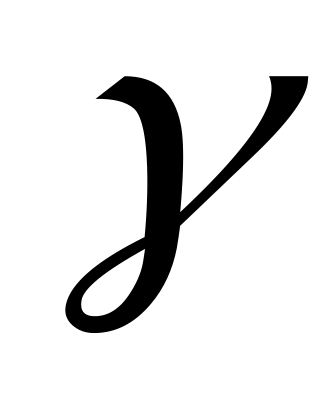 взаимно просты, существуют
взаимно просты, существуют  и
и  такие, что
такие, что 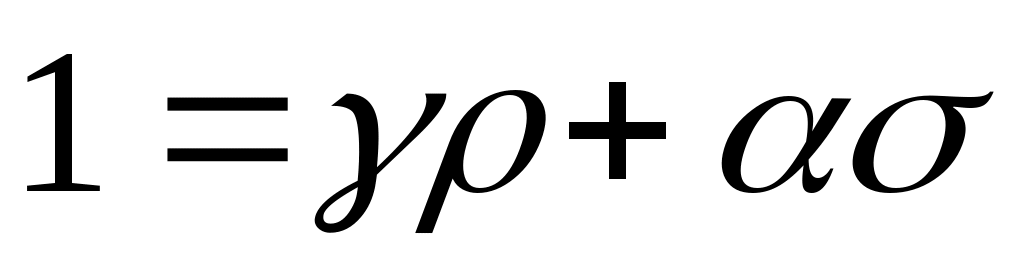 . Таким образом
. Таким образом
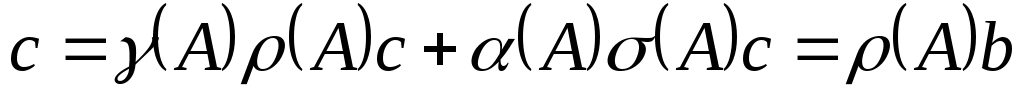 .
.
Если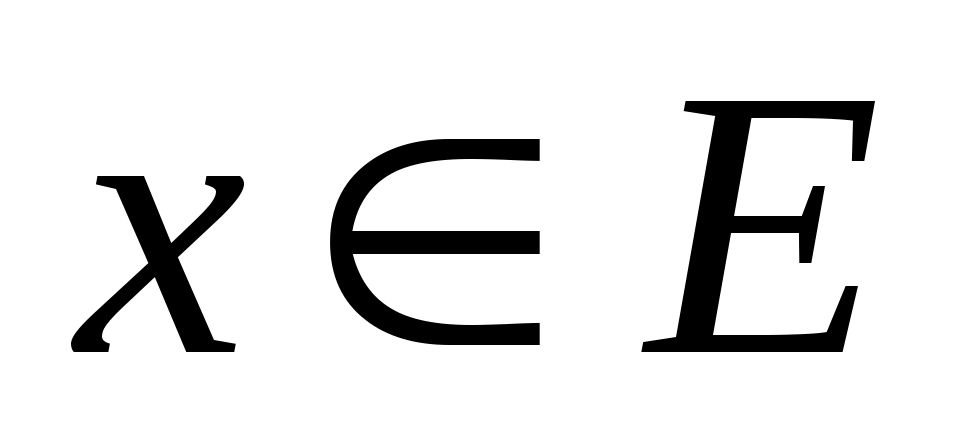 произвольно, то для некоторого полинома
произвольно, то для некоторого полинома 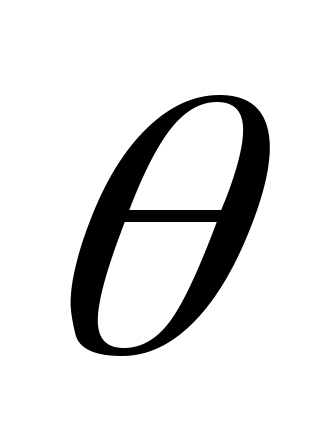 ,
,
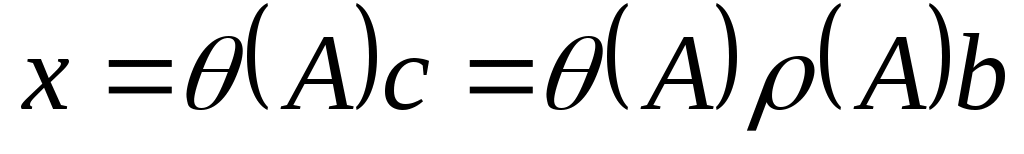 ;
;
тогда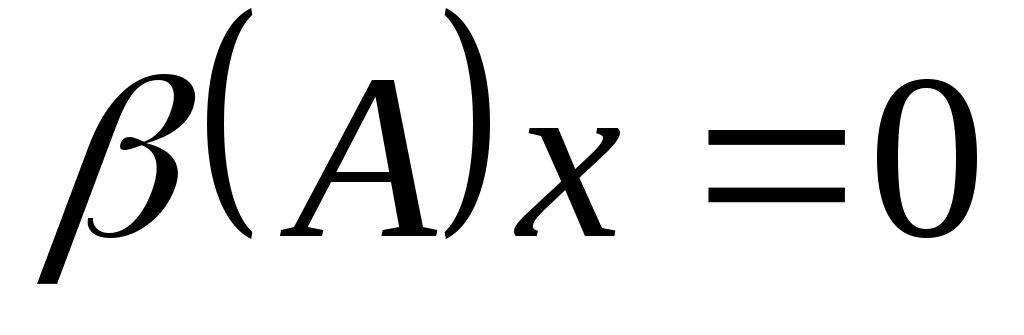 , и поэтому
, и поэтому 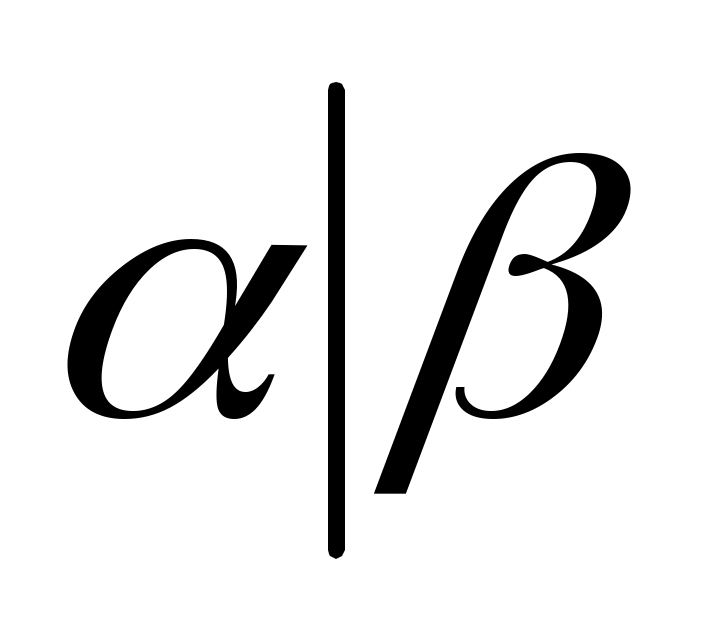
( делит
делит  ). Поскольку
). Поскольку  - минимальный многочлен
- минимальный многочлен  ,
, 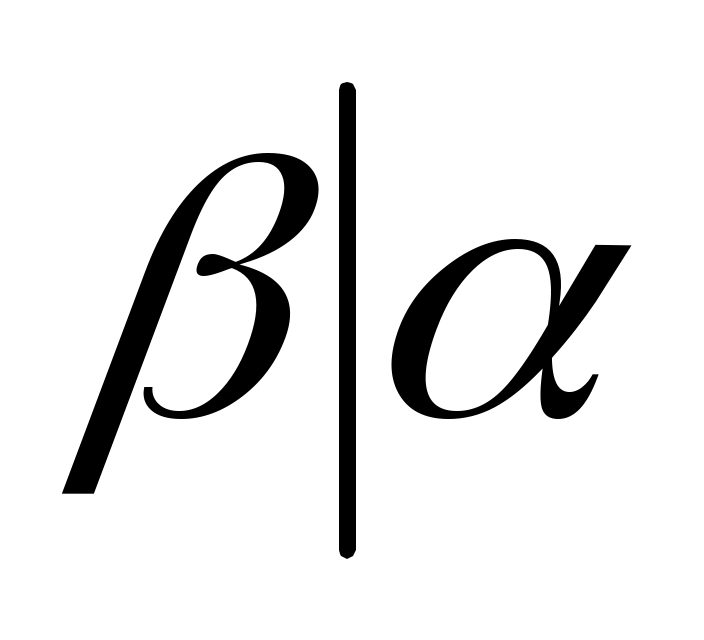 . Следовательно,
. Следовательно, 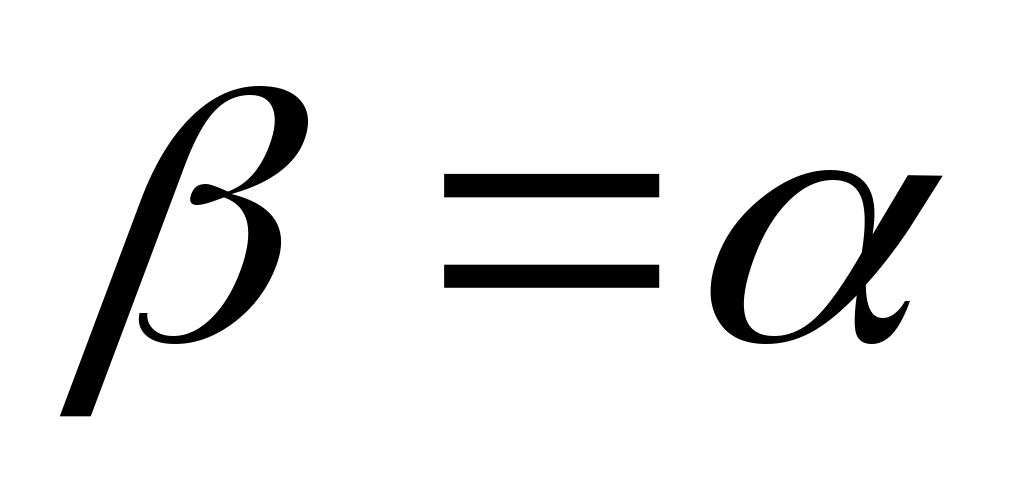 , и поэтому
, и поэтому 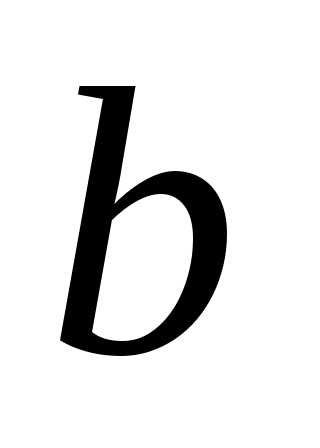 генерирует
генерирует  . Доказательство завершено.
. Доказательство завершено.
Пусть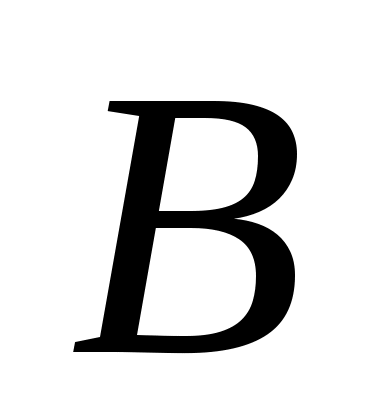 - матрица
- матрица  , как и раньше, и пусть
, как и раньше, и пусть 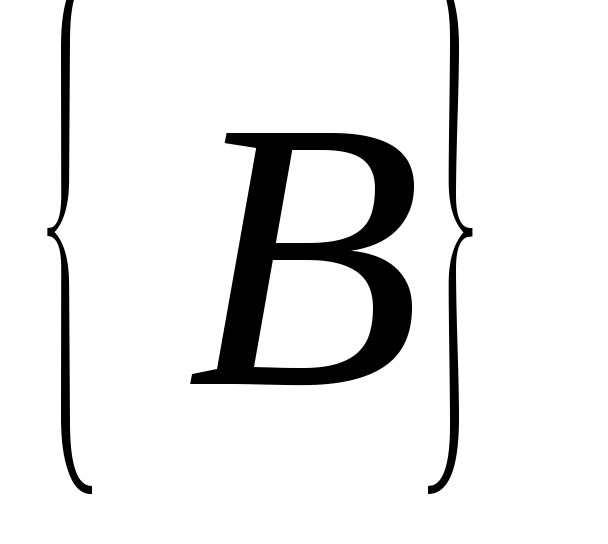 обозначает подпространство
обозначает подпространство  , натянутое на векторы столбцов
, натянутое на векторы столбцов 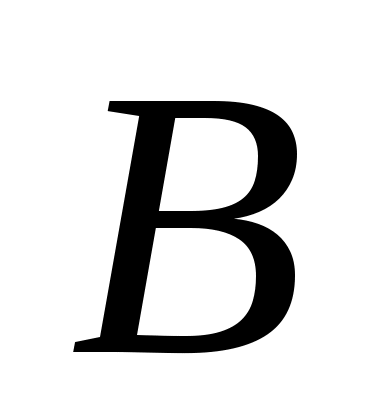 . Очевидно, что если
. Очевидно, что если 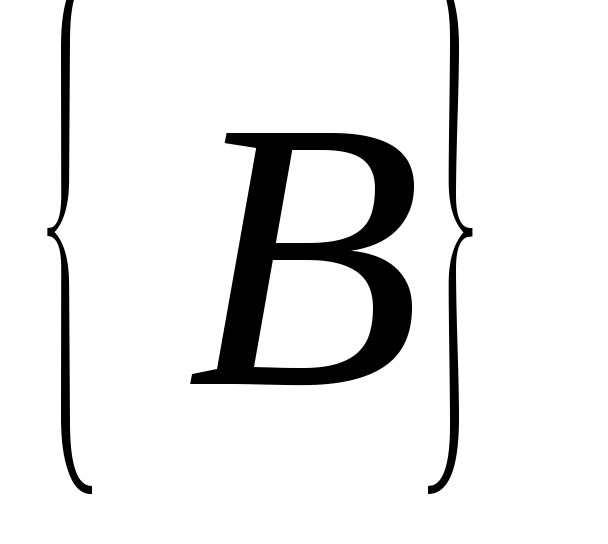 содержит генератор
содержит генератор  , то
, то 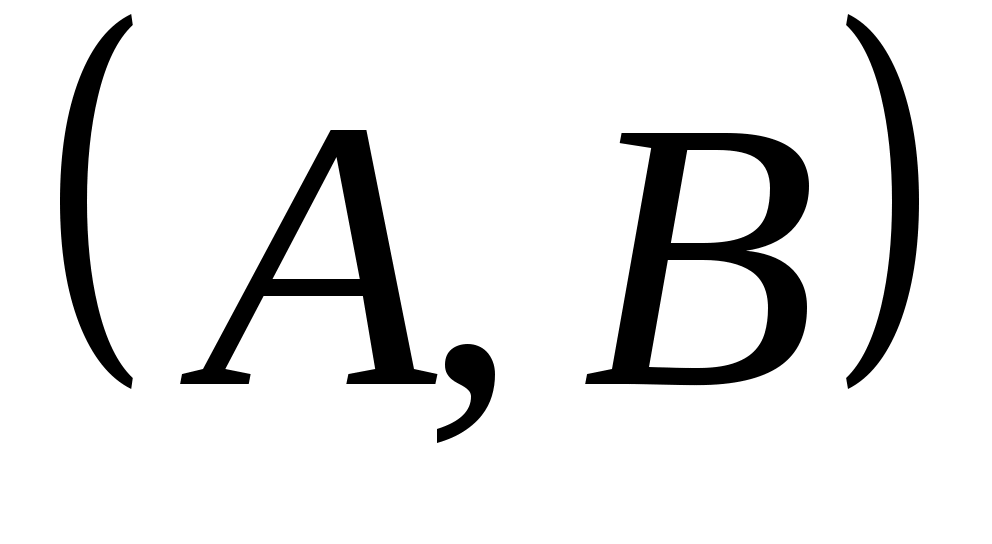 является управляемым. Поскольку минимальный полином из
является управляемым. Поскольку минимальный полином из  может иметь степень меньше
может иметь степень меньше 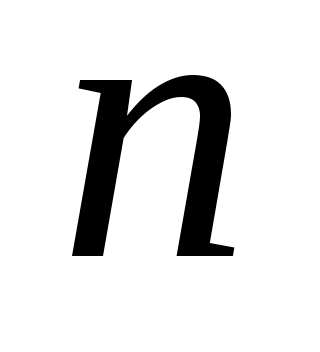 , обратное утверждение в общем случае ложно. Однако для циклического пространства верно следующее.
, обратное утверждение в общем случае ложно. Однако для циклического пространства верно следующее.
ЛЕММА 3: Пусть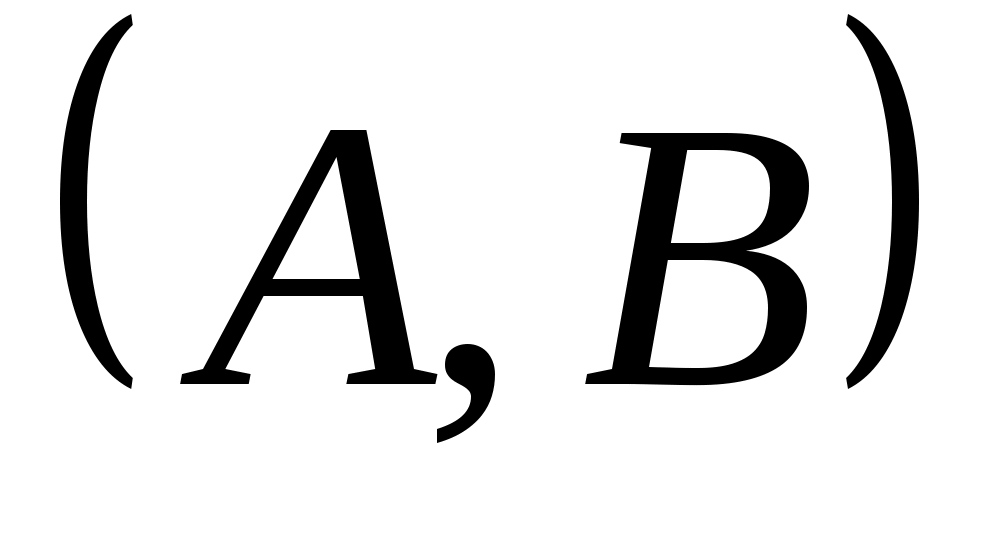 управляемо, а
управляемо, а  циклически. Существует такой вектор
циклически. Существует такой вектор 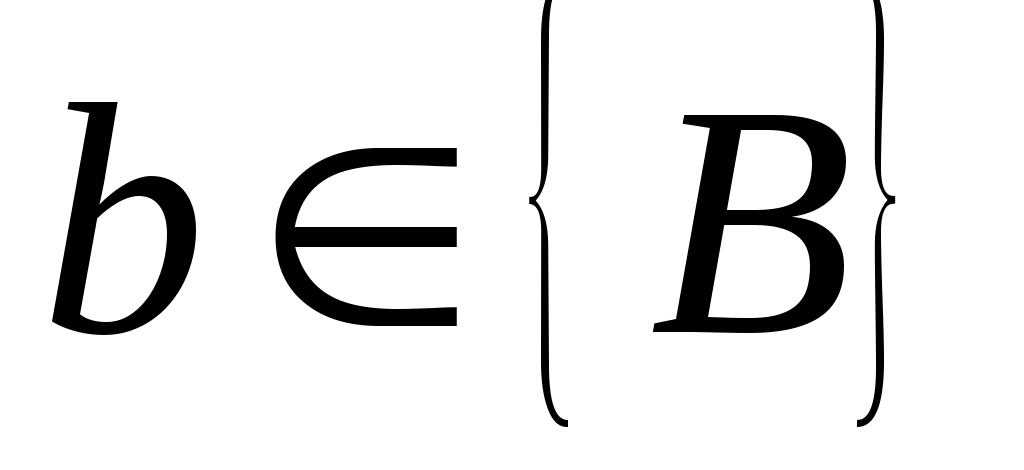 , что
, что 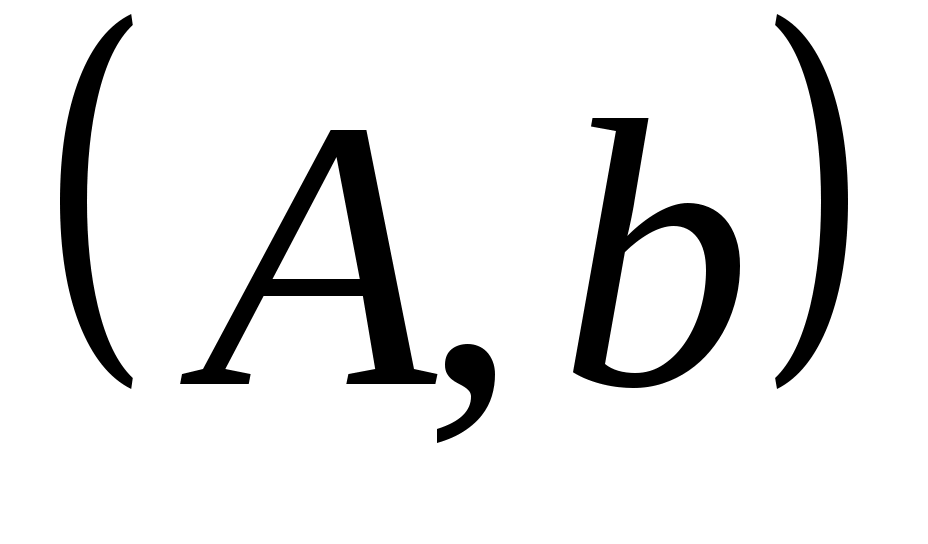 является управляемым.
является управляемым.
Доказательство: для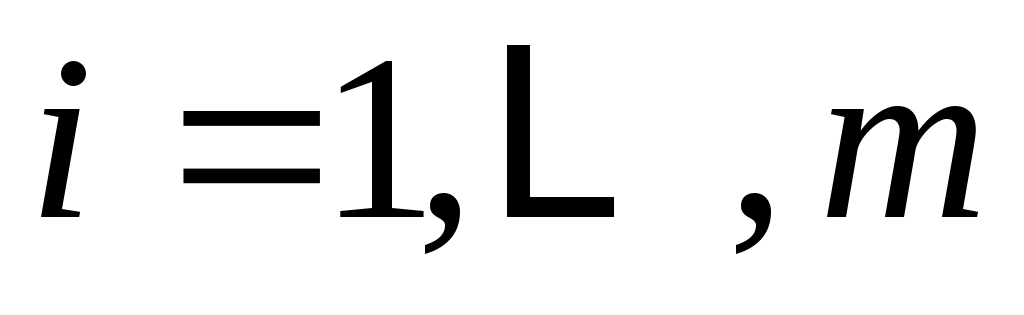 пусть
пусть 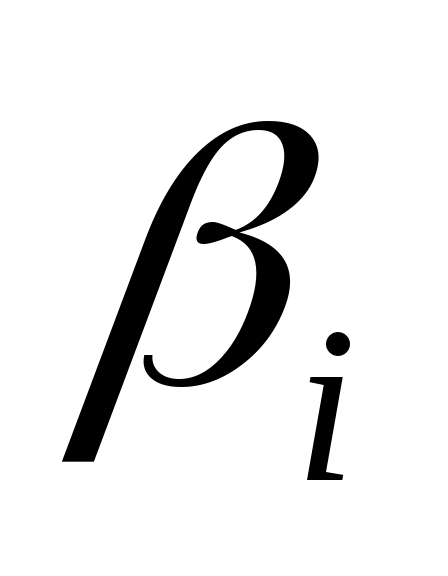 будет минимальный полином в
будет минимальный полином в 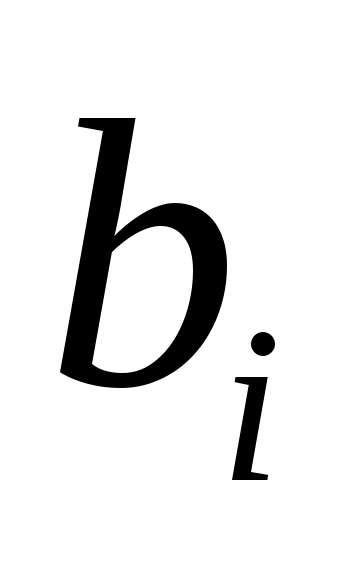 , а
, а 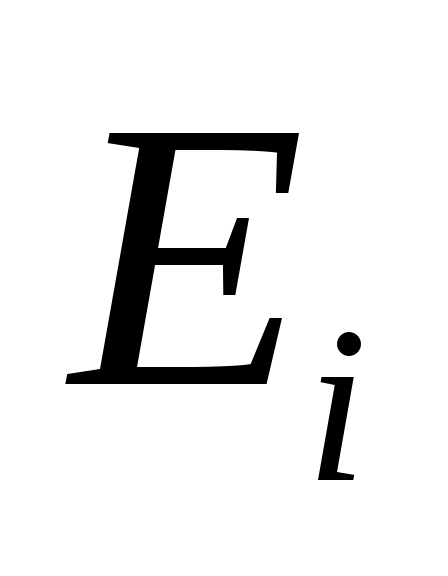 циклическое подпространство, порожденное
циклическое подпространство, порожденное 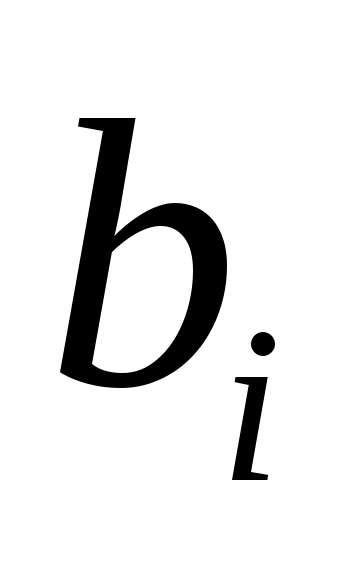 . Таким образом,
. Таким образом, 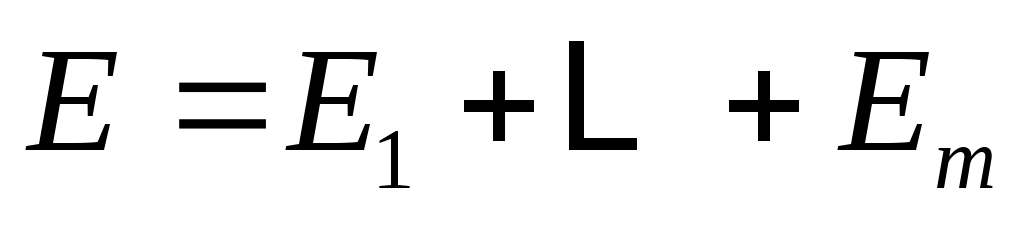 , и, если a является минимальный полином
, и, если a является минимальный полином  ,
,
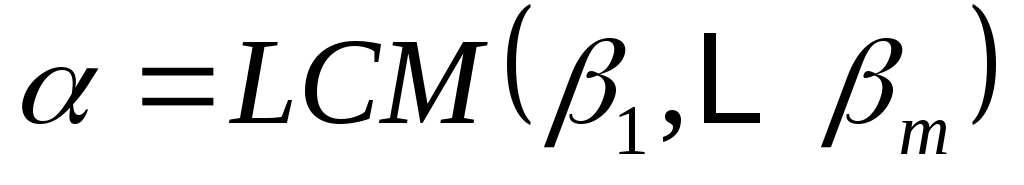 .
.
Пусть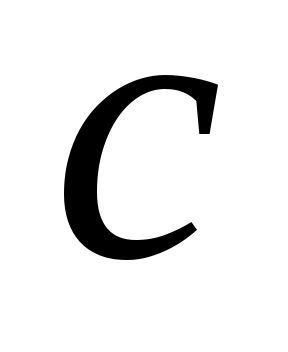 - будет генератором
- будет генератором  . Существуют многочлены
. Существуют многочлены 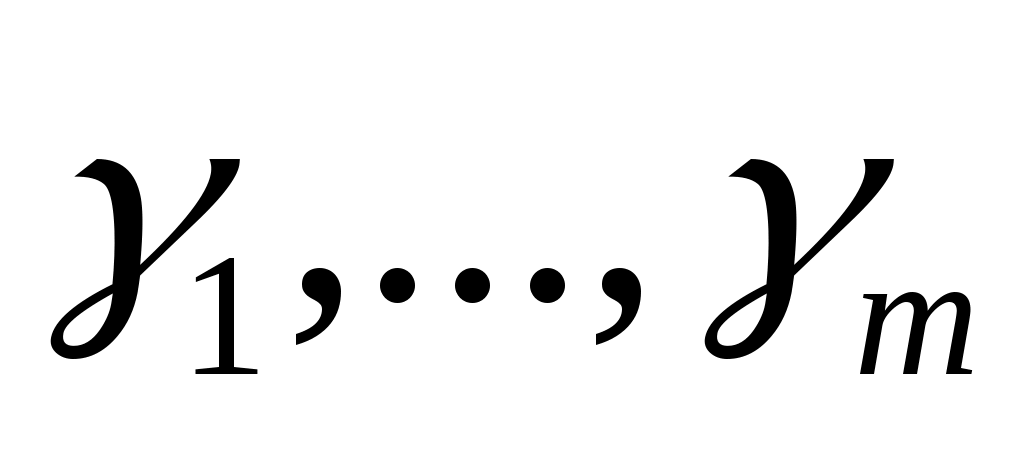 такое что
такое что 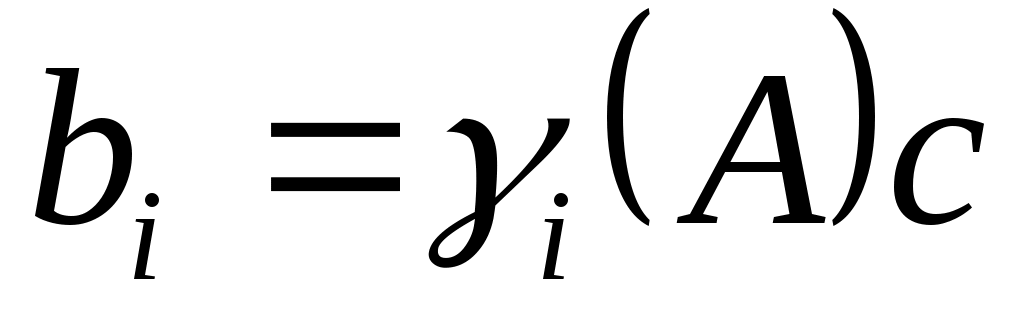 ,
, 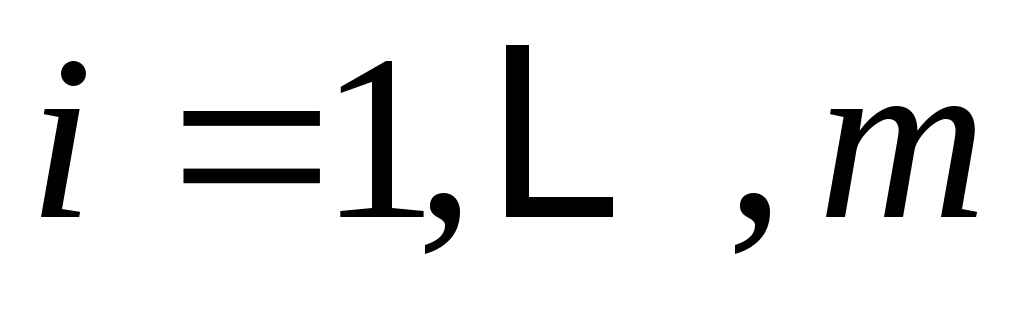 . Существование действительных чисел
. Существование действительных чисел 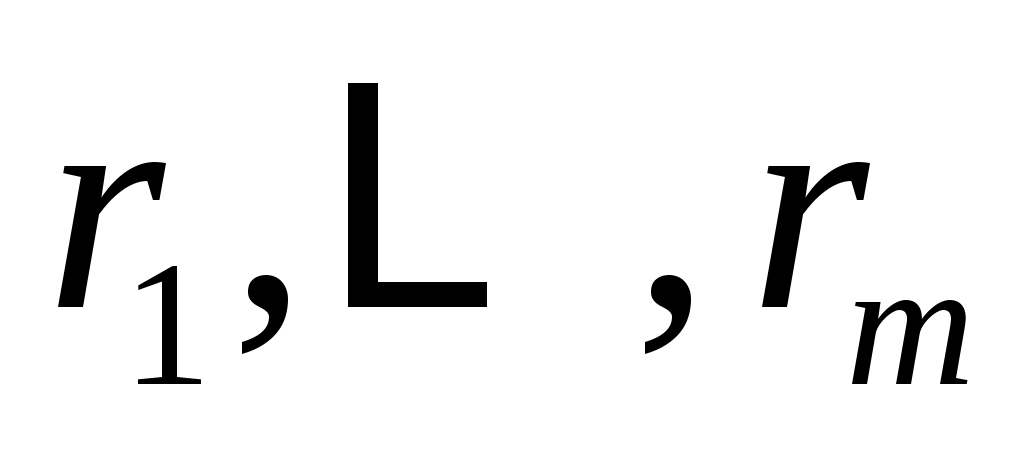 , будет доказано, что
, будет доказано, что 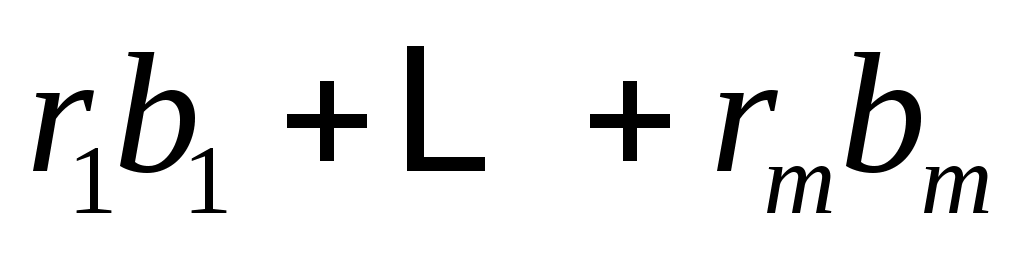 генерирует
генерирует  . По лемме 2 достаточно выбрать
. По лемме 2 достаточно выбрать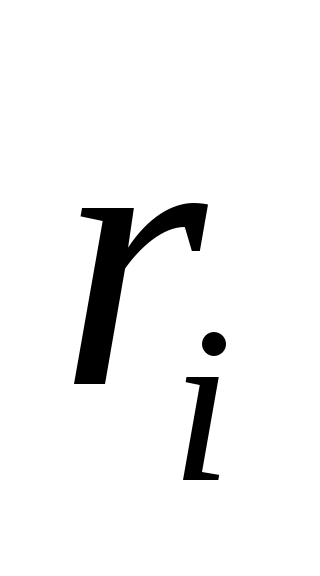 так, чтобы
так, чтобы
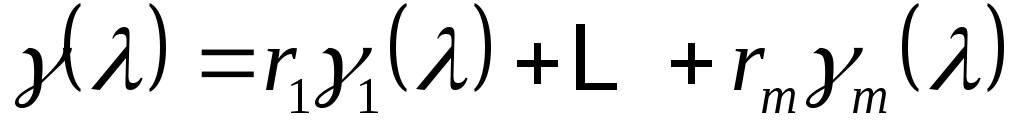
взаимно с .
.
Для этого сначала отметим, что
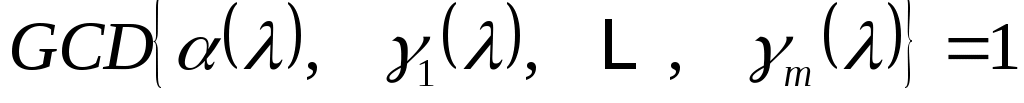 . (5)
. (5)
На самом деле, если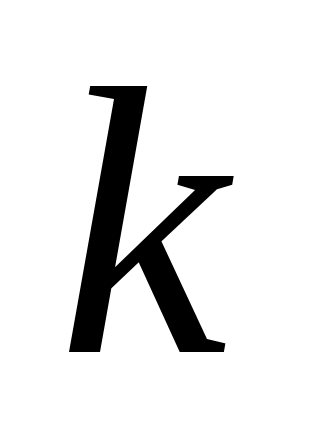 это наибольший общий делитель слева, то
это наибольший общий делитель слева, то
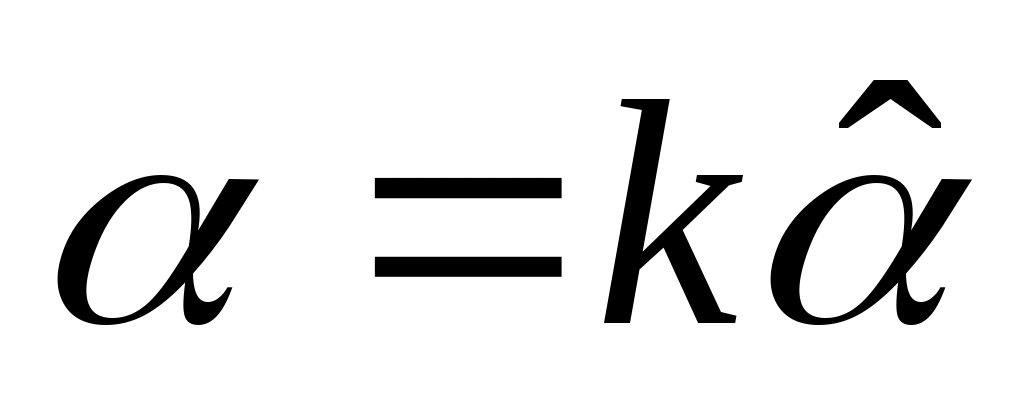
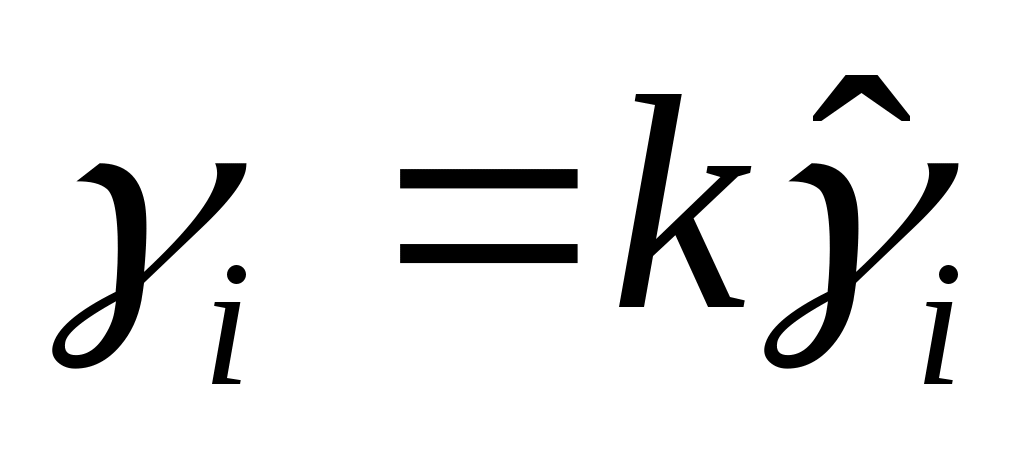 ,
, 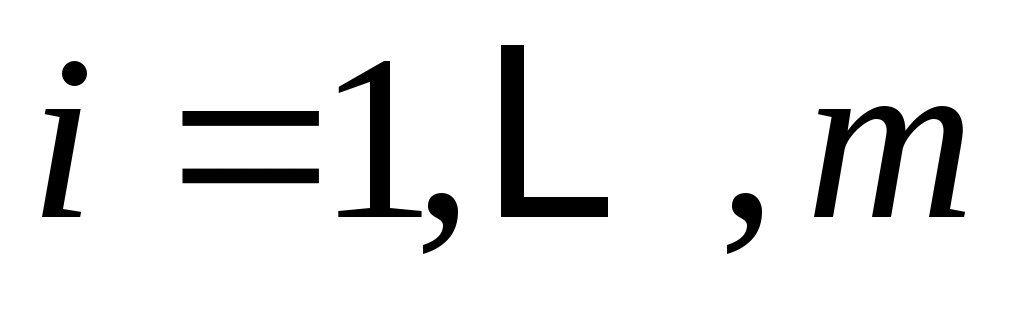
для подходящих полиномов и
и  . Потом
. Потом
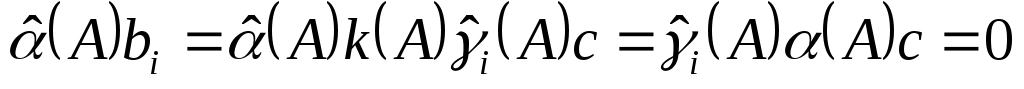 ,
, 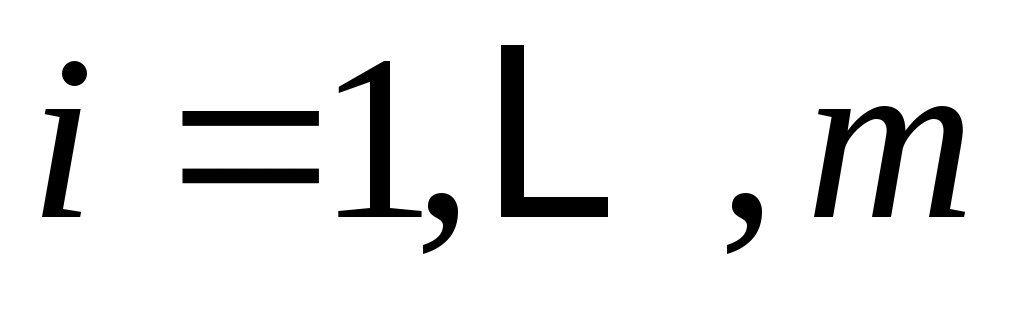 .
.
Таким образом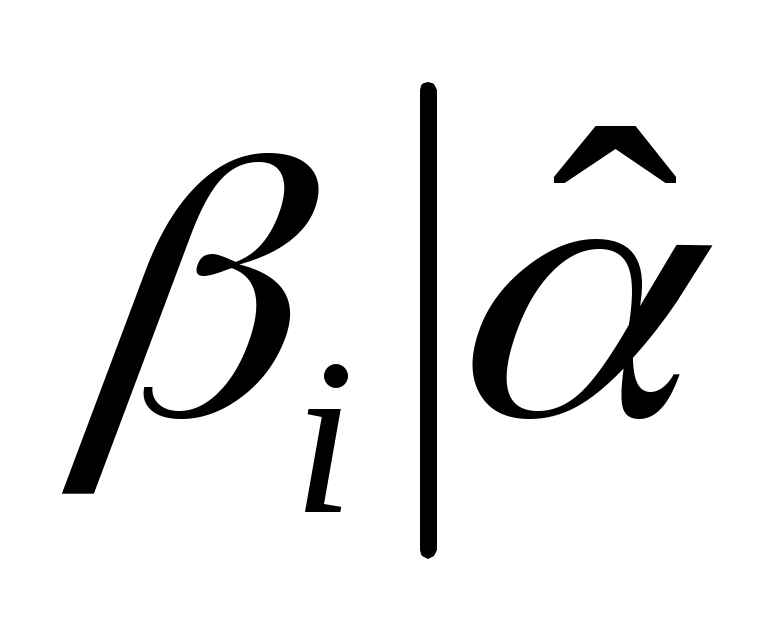 ,
, 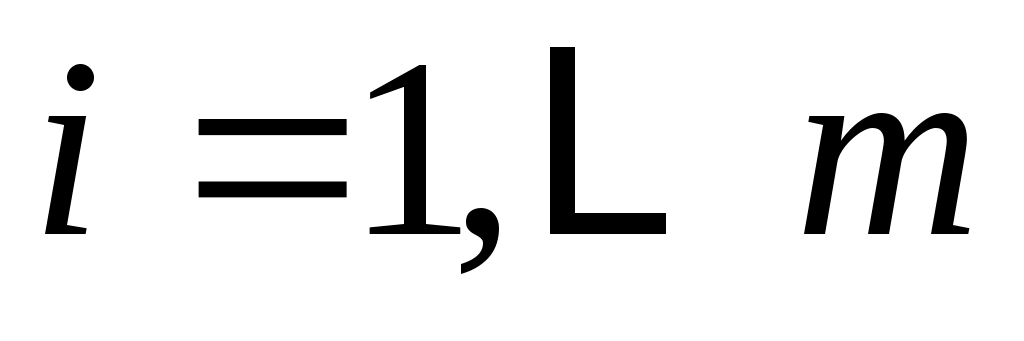 ; следовательно, по определению наименьшим общим кратным,
; следовательно, по определению наименьшим общим кратным,  , то есть
, то есть 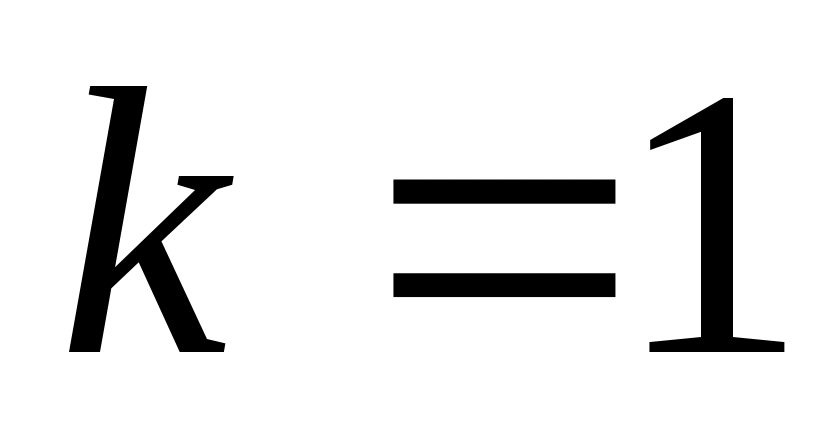 .
.
Наконец, обратите внимание, что и
и  взаимно просты тогда и только тогда, когда
взаимно просты тогда и только тогда, когда 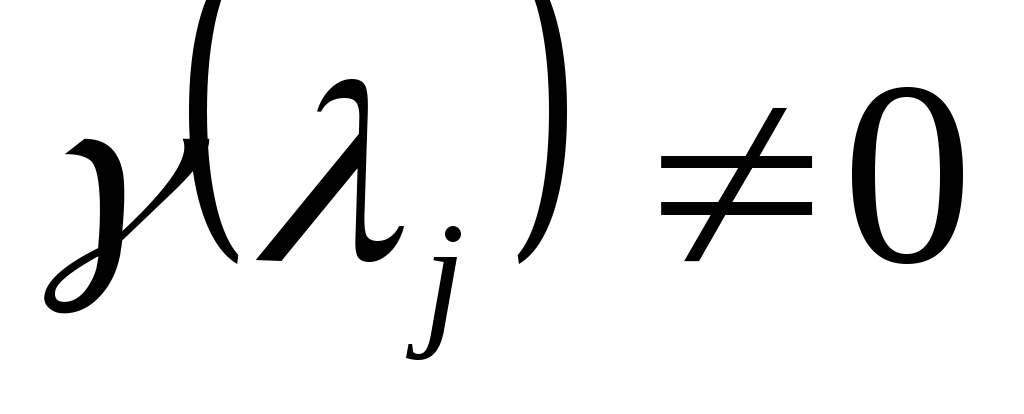 ,
, 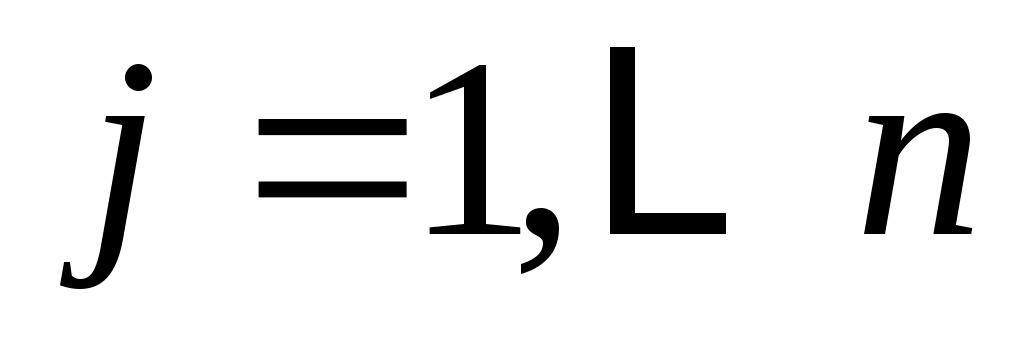 , где
, где  - (комплексные) нули
- (комплексные) нули 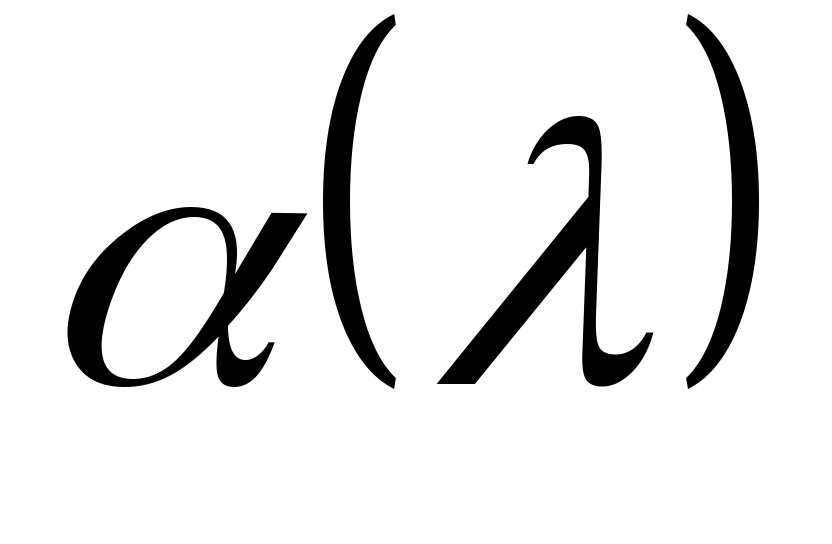 . В силу (5) величины
. В силу (5) величины 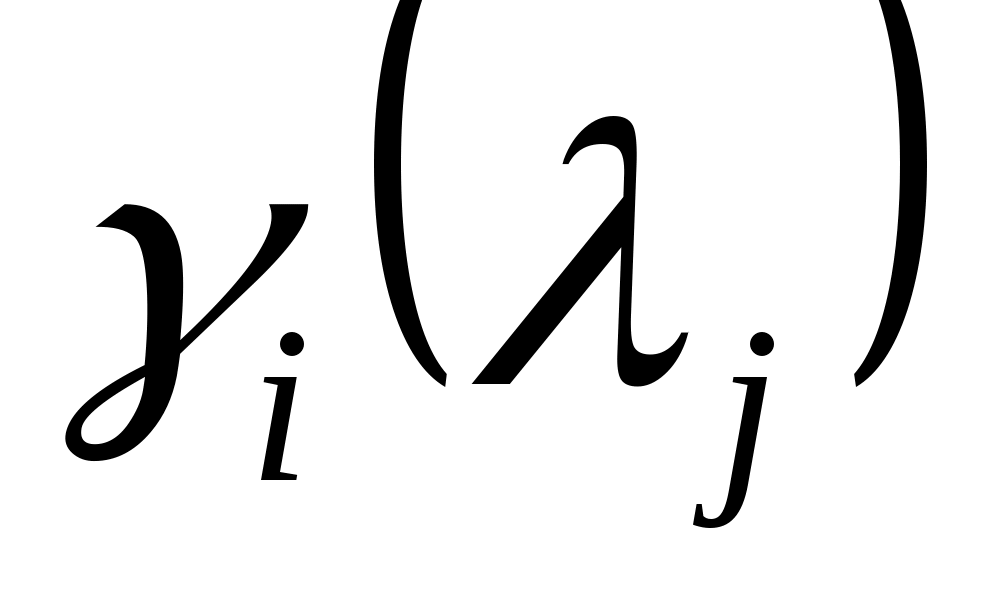 ,
,  , не могут все обращаться в нуль для любого
, не могут все обращаться в нуль для любого  . Следовательно, числа
. Следовательно, числа 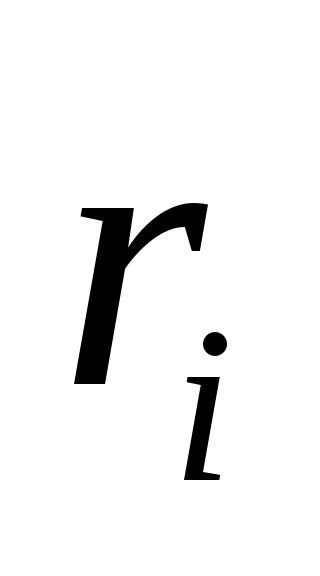
ЛЕММА 1: если минимальныйполином
В частности, условие леммы 1 выполняется, если собственные значения
Два нормированных полинома
, что
ЛЕММА 2: Пусть
Обратное тоже верно, но не нужно.
Доказательство: Пусть
Если
тогда
(
Пусть
ЛЕММА 3: Пусть
Доказательство: для
Пусть
взаимно с
Для этого сначала отметим, что
На самом деле, если
для подходящих полиномов
Таким образом
Наконец, обратите внимание, что

