ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.04.2024
Просмотров: 181
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
относится к интенсивным параметрам, ее измерение осуществляется с использованием экстенсивных свойств вещества. Например, через изменение объема в жидкостных термометрах или электрического сопротивления в термометрах сопротивления, через изменение ЭДС в спае термопары и т.п.
На практике используются две температурные шкалы (рис.1.7). Абсолютная шкала температур Кельвина – ее нижняя граница соответствует точке абсолютного нуля, где отсутствует молекулярное движение (практически недостижима) и единственной экспериментальной точкой принята тройная точка воды, лежащая выше точки таяния льда при нормальном атмосферном давлении (760 мм рт.ст.) на 0,01 о, этой точке присвоено значение температуры 273,16 К. Это значение выбрано для того, чтобы разность температур кипения и таяния химически чистой воды при нормальном физическом давлении составляла 100 о. Температура в кельвинах соответствует СИ и обозначается как Т К.
В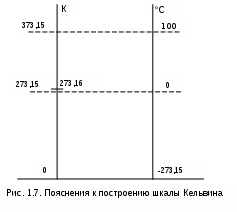
торая – стоградусная шкала температур Цельсия – широко используется в практике. Эта шкала имеет две опытные точки: 0 оС и 100 оС, она всем хоошо известна. Температура на ней обозначается как t оС. Между абсолютной температурой по шкале Кельвина и температурой по шкале Цельсия имеется соотношение:
T = t + 273,15 . (1.11)
Из (1.11) следует, что температуре 0 оС соответствует температура +273,15 К; а 0 К соответствует -273,15 оС.
В англоязычных странах и США используется шкала Фаренгейта, для которой справедливо соотношение F = 1,8t + 32.
В дальнейшем изложении материала будет использоваться абсолютная шкала температур Кельвина, как и требует Международная система единиц (СИ). В тех случаях, где практическая целесообразность диктует использование шкалы Цельсия, она будет приводиться совместно со шкалой Кельвина.
1.3. Основные понятия, характеризующие
термодинамическую систему
1.3.1. Равновесные и неравновесные состояния
термодинамических тел и систем
Термодинамически равновесное состояние тела или системы – это такое состояние теплового и механического равновесий элементов тела или системы, которое без внешнего воздействия может сохраняться сколь угодно долго.
Равновесная система – это система тел, находящихся в термодинамическом равновесии, в противном случае она будет называться неравновесной системой.
Так, без учета гравитационных сил равновесное состояние тела или системы есть такое их состояние, при котором по всему их объему давления и температуры имеют одни значения. Равенство только давления во всех точках обусловливает механическое равновесие, равенство температур – термическое равновесие.
При неравновесном состоянии тела (системы) в разных его частях могут быть различны и температуры, и давления. Однако в неравновесной системе могут быть точки, в которых некоторые термические параметры одинаковы.Геометрическое место точек в пространстве, занимаемом системой (телом), с одинаковыми температурами представляет собой изотермическую поверхность, а с одинаковым давлением – изобарическую поверхность. Такие поверхности называютсяизопотенциальными. Изопотенциальные поверхности не могут пересекаться. Изопотенциальные поверхности могут быть и при равновесном состоянии тела. Например, в высоком цилиндре с жидкостью на различных уровнях от его дна будут различные изобарные поверхности, обусловленные действием гравитационного поля Земли. Поэтому равенство параметров в равновесной системе делается с оговоркой – без учета гравитационных сил.
Все термодинамические параметры гомогенной сисемы (однородной – с одинаковыми физическими свойствами), находящейся в равновесном состоянии, имеют определенную функциональную связь. При отсутствии действия внешних полей термодинамически равновесное состояние любого однородного реального тела определяется всего лишь двумя независимыми параметрами. Для неоднородных систем могут два параметра взаимно определять друг друга (например, давление и температура влажного насыщенного пара), в этом случае необходим третий параметр.
В качестве независимых параметров могут быть выбраны: давление и температура, давление и удельный объём или любая пара независимых свойств (температура и энтропия, давление и энтальпия и т.п.).
При заданных значениях двух параметров термодинмически равновесной системы можно определить любые другие ее параметры. Связь между параметрами такой системы описывается уравнениями состояния. Например, связь между параметрами p, v, T может быть выражена термическими уравнениями состояния системы:
- в неявной форме f(p,v,T) = 0 , (1.12)
- в явной форме p = F(v,T); v = f(p,T); T = j(p,v). (1.13)
В системе координат P,v,T эти уравнения описывают поверхность, называемую термодинамической (рис. 1.8).
В
ид функциональной зависимости между параметрами различен для различных веществ и может быть получен либо из опыта, либо на базе микрофизических теорий. Методами самой термодинамики эта связь определена быть не может.
Взаимосвязь свойств однородного вещества в равновесном состоянии может также характеризоваться термическими коэффициентами. Эти коэффициенты могут быть определены опытным путем, они имеют определенный физический смысл.
Взаимосвязь термических коэффициентов можно получить, используя уравнение состояния вещества в явном виде Р=F(v,T), представив его как полный дифференциал
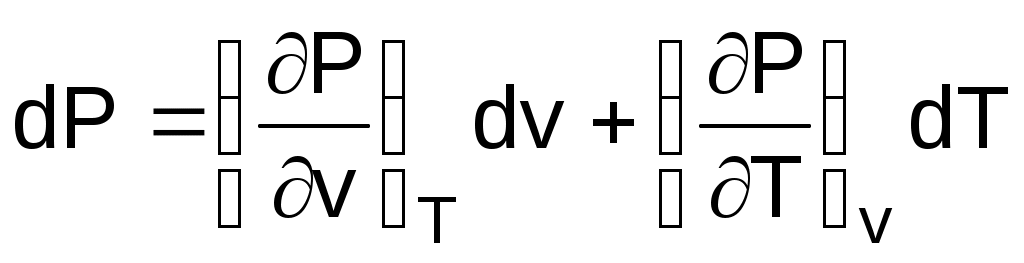; (1.14)
приняв Р = const, получим
,
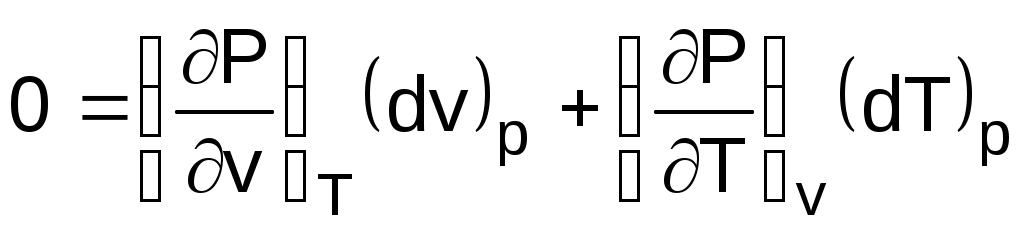преобразовав это выражение, получим соотношение вида
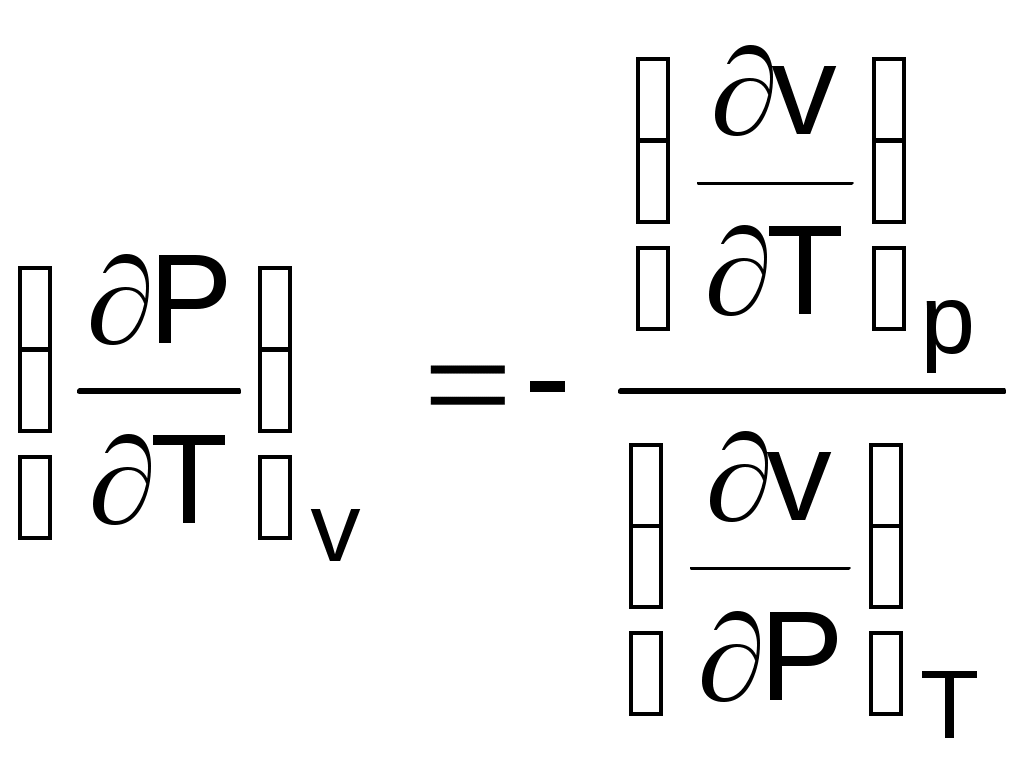. (1.15)
В выражении (1.15) отношение (dv/dP)T характеризует интенсивность изменения объема в зависимости от изменения давления при постоянной температуре. Отношение этой величины к удельному объему vo, взятому при фиксированном состоянии (например, при нормальных условиях) с обратным знаком, называется коэффициентом изотермическойсжимаемости и обозначается как :
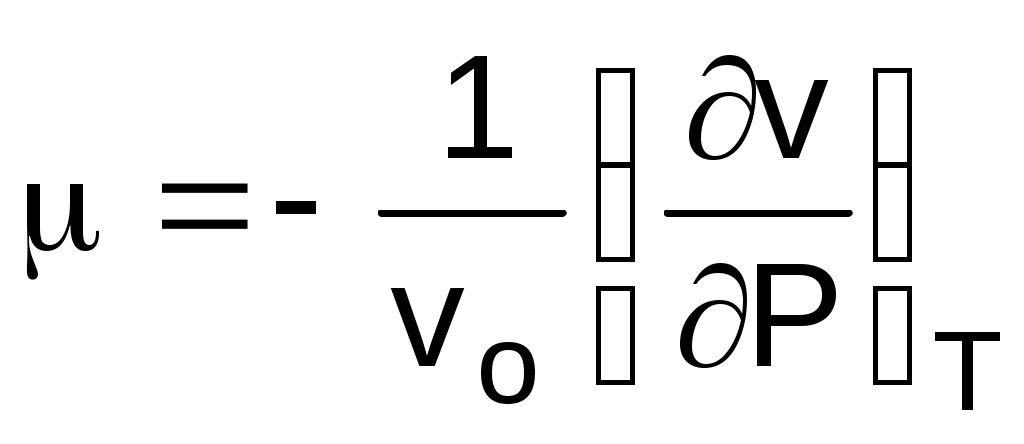. (1.16)
Отношение (dv/dТ)Р характеризует интенсивность изменения объема в зависимости от изменения температуры при постоянном давлении. Разделив его на vо, получим коэффициент изобарного расширения, обозначающийся как :
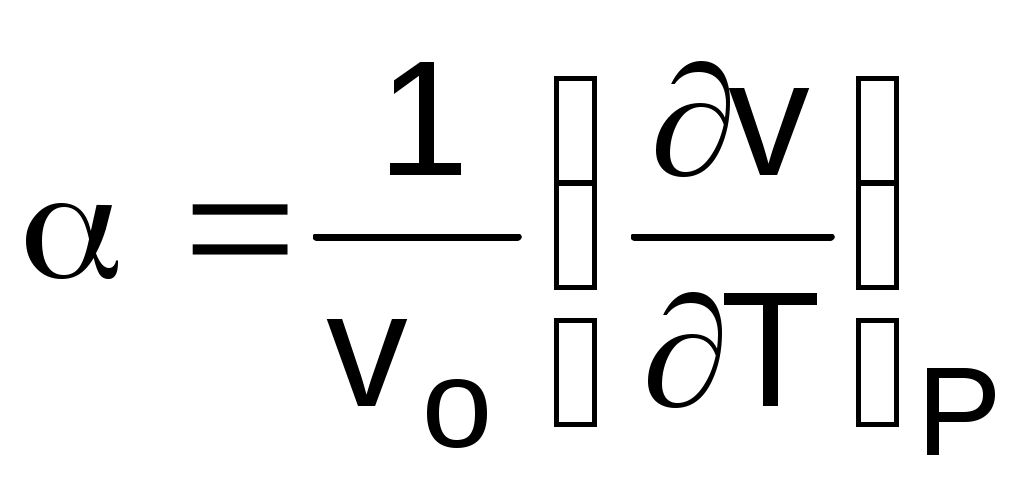. (1.17)
Отношение (dР/dТ)v характеризует изменение давления в зависимости от изменения температуры при постоянном объеме. Разделив его на Ро, получим коэффициент упругости, обозначающийся как :
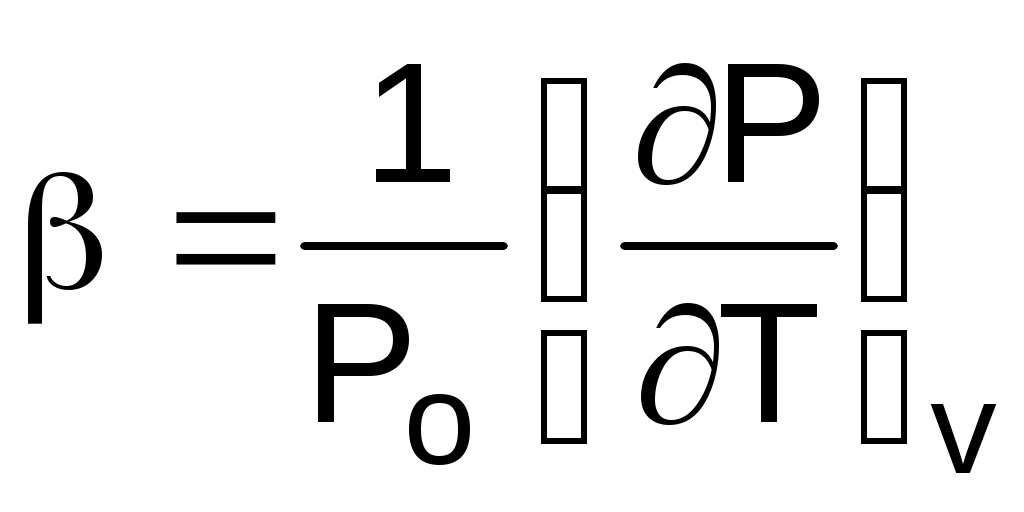. (1.18)
Выразив значения частных производных в выражении (1.15) через термические коэффициенты (dv/dP)T=-vo , (dv/dТ)P=vo , (dР/dТ)v=Po и подставив их в (1.15), получим уравнение взаимосвязи термических коэффициентов:
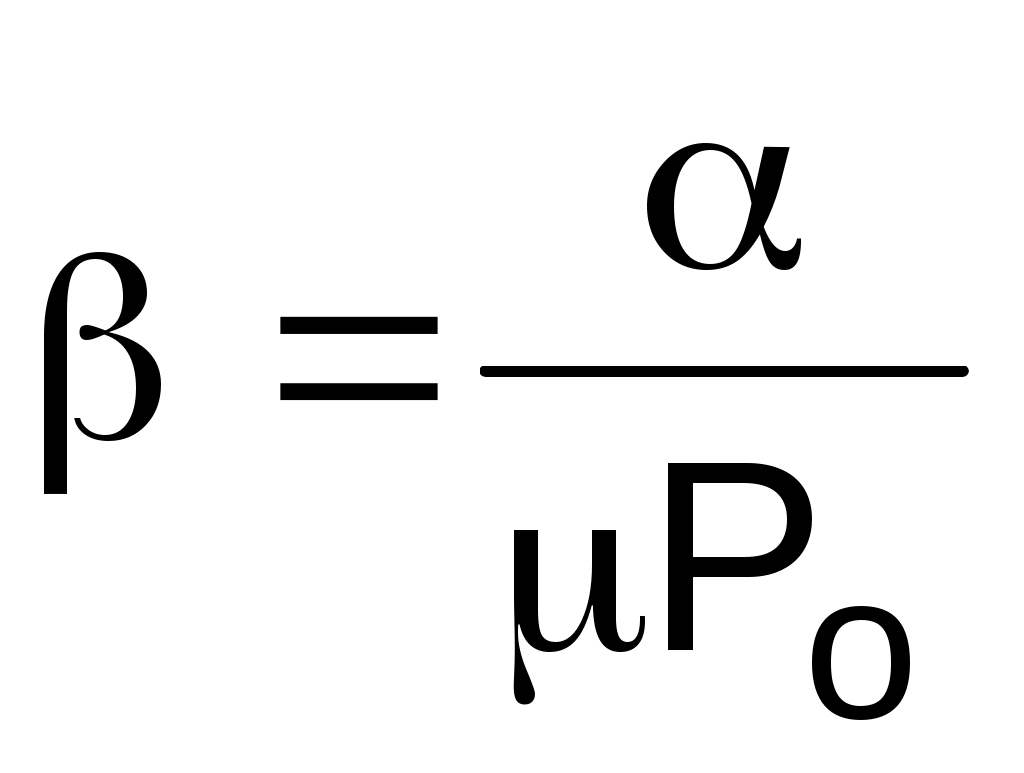. (1.19)
Выражение (1.19), как и уравнение состояния, описывает свойства вещества. Кроме этого, выражение (1.19) необходимо для расчета коэффициента твердых и жидких тел, поскольку эти тела невозможно нагреть без изменения их объема, т.е. для них опытным путем определить невозможно.
1.3.4. Термодинамический процесс
Понятие термодинамического процесса характеризует термодинамическую систему с точки зрения ее энергетического взаимодействия с окружающей средой.
Термодинамическим процессомназывается процесс изменения состояния термодинамического тела (системы), не находящегося в термодинамическом равновесии с внешней средой и не изолированного от нее. При этом наблюдается энергетическое взаимодействие между телом и окружающей средой, сопровождающееся изменением параметров тела.
Строго говоря, только для процессов, происходящих очень медленно, с малыми отклонениями промежуточных параметров (квазистатические равновесные процессы), можно воспользоваться уравнениями состояния, а сам процесс геометрически представить в виде непрерывной кривой на термодинамической поверхности. Графическое изображение действительных неравновесных процессов, протекающих с конечной скоростью, имеет условный характер. Понятие равновесности характеризует поведение параметров внутри и на границах тел при процессах, но не затрагивает превращения форм энергии и распределения ее в системе. Для характеристики процессов с точки зрения превращения и распределения энергии между всеми телами, участвующими в процессе, вводится понятие обратимости процессов.
Обратимыми называются процессы, которые могут быть проведены в прямом и обратном направлениях таким образом, что все тела, участвующие в процессе, проходят через одни и те же промежуточные равновесные состояния (но в обратной последовательности), а после проведения прямого и обратного процессов все тела закрытой изолированной системы возвращаются в первоначальное состояние, и, следовательно, распределение энергии между ними оказывается прежним.
Процессы, не отвечающие поставленным условиям, называются необратимыми.
Все неравновесные процессы необратимы. Так, при неравенстве давления в рабочем теле и внешнего давления рабочее тело расширяется или сжимается, в результате возникают вихревые движения, которые со временем успокаиваются, а их энергия переходит в энергию теплового движения частиц. В этом случае наблюдается переход механической работы в теплоту, в результате чего для возврата системы в первоначальное состояние потребуется дополнительное количество механической работы.
При отсутствии термического равновесия процесс также необратим. Теплота самопроизвольно переходит от тела более нагретого к телу менее нагретому, и обратный переход теплоты возможен только при наличии дополнительного источника теплоты.
Необратимость процессов подразделяется:
- на внешнюю необратимость, вызванную разностью температур при теплообмене между телами;
- внутреннюю необратимость, вызванную наличием трения. В прямом и обратном процессах в этом случае имеется работа, затрачиваемая на трение, она превращается в теплоту.
На практике используются две температурные шкалы (рис.1.7). Абсолютная шкала температур Кельвина – ее нижняя граница соответствует точке абсолютного нуля, где отсутствует молекулярное движение (практически недостижима) и единственной экспериментальной точкой принята тройная точка воды, лежащая выше точки таяния льда при нормальном атмосферном давлении (760 мм рт.ст.) на 0,01 о, этой точке присвоено значение температуры 273,16 К. Это значение выбрано для того, чтобы разность температур кипения и таяния химически чистой воды при нормальном физическом давлении составляла 100 о. Температура в кельвинах соответствует СИ и обозначается как Т К.
В
торая – стоградусная шкала температур Цельсия – широко используется в практике. Эта шкала имеет две опытные точки: 0 оС и 100 оС, она всем хоошо известна. Температура на ней обозначается как t оС. Между абсолютной температурой по шкале Кельвина и температурой по шкале Цельсия имеется соотношение:
T = t + 273,15 . (1.11)
Из (1.11) следует, что температуре 0 оС соответствует температура +273,15 К; а 0 К соответствует -273,15 оС.
В англоязычных странах и США используется шкала Фаренгейта, для которой справедливо соотношение F = 1,8t + 32.
В дальнейшем изложении материала будет использоваться абсолютная шкала температур Кельвина, как и требует Международная система единиц (СИ). В тех случаях, где практическая целесообразность диктует использование шкалы Цельсия, она будет приводиться совместно со шкалой Кельвина.
1.3. Основные понятия, характеризующие
термодинамическую систему
1.3.1. Равновесные и неравновесные состояния
термодинамических тел и систем
Термодинамически равновесное состояние тела или системы – это такое состояние теплового и механического равновесий элементов тела или системы, которое без внешнего воздействия может сохраняться сколь угодно долго.
Равновесная система – это система тел, находящихся в термодинамическом равновесии, в противном случае она будет называться неравновесной системой.
Так, без учета гравитационных сил равновесное состояние тела или системы есть такое их состояние, при котором по всему их объему давления и температуры имеют одни значения. Равенство только давления во всех точках обусловливает механическое равновесие, равенство температур – термическое равновесие.
При неравновесном состоянии тела (системы) в разных его частях могут быть различны и температуры, и давления. Однако в неравновесной системе могут быть точки, в которых некоторые термические параметры одинаковы.Геометрическое место точек в пространстве, занимаемом системой (телом), с одинаковыми температурами представляет собой изотермическую поверхность, а с одинаковым давлением – изобарическую поверхность. Такие поверхности называютсяизопотенциальными. Изопотенциальные поверхности не могут пересекаться. Изопотенциальные поверхности могут быть и при равновесном состоянии тела. Например, в высоком цилиндре с жидкостью на различных уровнях от его дна будут различные изобарные поверхности, обусловленные действием гравитационного поля Земли. Поэтому равенство параметров в равновесной системе делается с оговоркой – без учета гравитационных сил.
1.3.2. Уравнение состояния термодинамической системы
Все термодинамические параметры гомогенной сисемы (однородной – с одинаковыми физическими свойствами), находящейся в равновесном состоянии, имеют определенную функциональную связь. При отсутствии действия внешних полей термодинамически равновесное состояние любого однородного реального тела определяется всего лишь двумя независимыми параметрами. Для неоднородных систем могут два параметра взаимно определять друг друга (например, давление и температура влажного насыщенного пара), в этом случае необходим третий параметр.
В качестве независимых параметров могут быть выбраны: давление и температура, давление и удельный объём или любая пара независимых свойств (температура и энтропия, давление и энтальпия и т.п.).
При заданных значениях двух параметров термодинмически равновесной системы можно определить любые другие ее параметры. Связь между параметрами такой системы описывается уравнениями состояния. Например, связь между параметрами p, v, T может быть выражена термическими уравнениями состояния системы:
- в неявной форме f(p,v,T) = 0 , (1.12)
- в явной форме p = F(v,T); v = f(p,T); T = j(p,v). (1.13)
В системе координат P,v,T эти уравнения описывают поверхность, называемую термодинамической (рис. 1.8).
В
ид функциональной зависимости между параметрами различен для различных веществ и может быть получен либо из опыта, либо на базе микрофизических теорий. Методами самой термодинамики эта связь определена быть не может.
1.3.3. Термические коэффициенты
Взаимосвязь свойств однородного вещества в равновесном состоянии может также характеризоваться термическими коэффициентами. Эти коэффициенты могут быть определены опытным путем, они имеют определенный физический смысл.
Взаимосвязь термических коэффициентов можно получить, используя уравнение состояния вещества в явном виде Р=F(v,T), представив его как полный дифференциал
; (1.14)приняв Р = const, получим
,преобразовав это выражение, получим соотношение вида
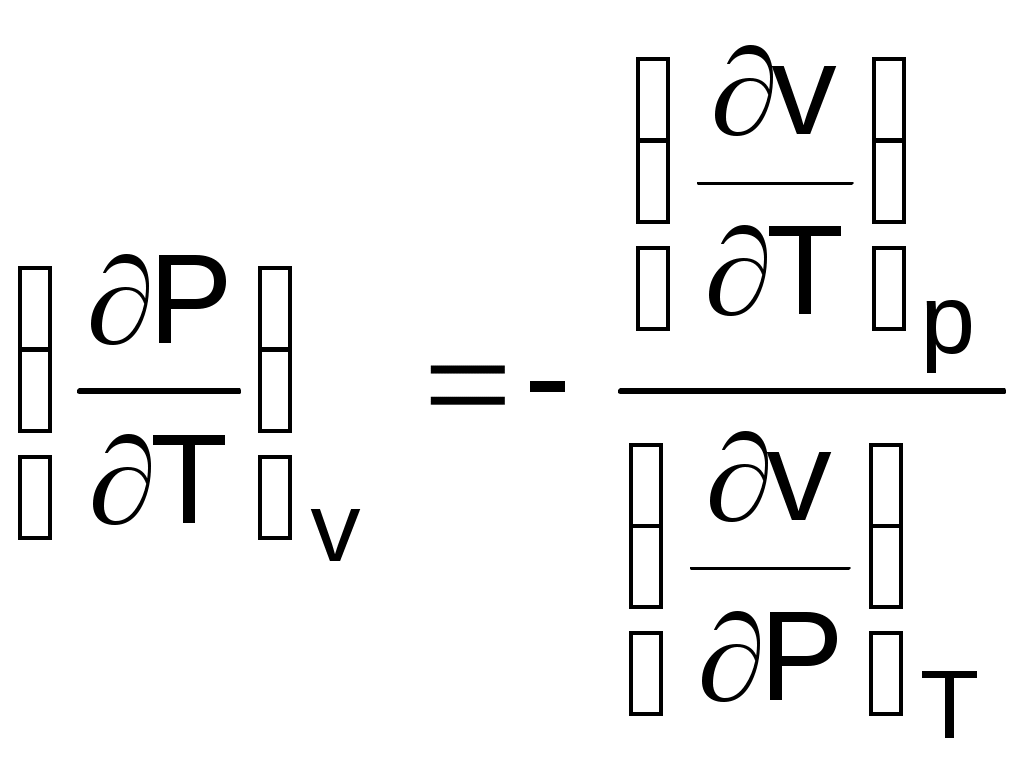. (1.15)В выражении (1.15) отношение (dv/dP)T характеризует интенсивность изменения объема в зависимости от изменения давления при постоянной температуре. Отношение этой величины к удельному объему vo, взятому при фиксированном состоянии (например, при нормальных условиях) с обратным знаком, называется коэффициентом изотермическойсжимаемости и обозначается как :
. (1.16)Отношение (dv/dТ)Р характеризует интенсивность изменения объема в зависимости от изменения температуры при постоянном давлении. Разделив его на vо, получим коэффициент изобарного расширения, обозначающийся как :
. (1.17)Отношение (dР/dТ)v характеризует изменение давления в зависимости от изменения температуры при постоянном объеме. Разделив его на Ро, получим коэффициент упругости, обозначающийся как :
. (1.18)Выразив значения частных производных в выражении (1.15) через термические коэффициенты (dv/dP)T=-vo , (dv/dТ)P=vo , (dР/dТ)v=Po и подставив их в (1.15), получим уравнение взаимосвязи термических коэффициентов:
. (1.19)Выражение (1.19), как и уравнение состояния, описывает свойства вещества. Кроме этого, выражение (1.19) необходимо для расчета коэффициента твердых и жидких тел, поскольку эти тела невозможно нагреть без изменения их объема, т.е. для них опытным путем определить невозможно.
1.3.4. Термодинамический процесс
Понятие термодинамического процесса характеризует термодинамическую систему с точки зрения ее энергетического взаимодействия с окружающей средой.
Термодинамическим процессомназывается процесс изменения состояния термодинамического тела (системы), не находящегося в термодинамическом равновесии с внешней средой и не изолированного от нее. При этом наблюдается энергетическое взаимодействие между телом и окружающей средой, сопровождающееся изменением параметров тела.
Строго говоря, только для процессов, происходящих очень медленно, с малыми отклонениями промежуточных параметров (квазистатические равновесные процессы), можно воспользоваться уравнениями состояния, а сам процесс геометрически представить в виде непрерывной кривой на термодинамической поверхности. Графическое изображение действительных неравновесных процессов, протекающих с конечной скоростью, имеет условный характер. Понятие равновесности характеризует поведение параметров внутри и на границах тел при процессах, но не затрагивает превращения форм энергии и распределения ее в системе. Для характеристики процессов с точки зрения превращения и распределения энергии между всеми телами, участвующими в процессе, вводится понятие обратимости процессов.
Обратимыми называются процессы, которые могут быть проведены в прямом и обратном направлениях таким образом, что все тела, участвующие в процессе, проходят через одни и те же промежуточные равновесные состояния (но в обратной последовательности), а после проведения прямого и обратного процессов все тела закрытой изолированной системы возвращаются в первоначальное состояние, и, следовательно, распределение энергии между ними оказывается прежним.
Процессы, не отвечающие поставленным условиям, называются необратимыми.
Все неравновесные процессы необратимы. Так, при неравенстве давления в рабочем теле и внешнего давления рабочее тело расширяется или сжимается, в результате возникают вихревые движения, которые со временем успокаиваются, а их энергия переходит в энергию теплового движения частиц. В этом случае наблюдается переход механической работы в теплоту, в результате чего для возврата системы в первоначальное состояние потребуется дополнительное количество механической работы.
При отсутствии термического равновесия процесс также необратим. Теплота самопроизвольно переходит от тела более нагретого к телу менее нагретому, и обратный переход теплоты возможен только при наличии дополнительного источника теплоты.
Необратимость процессов подразделяется:
- на внешнюю необратимость, вызванную разностью температур при теплообмене между телами;
- внутреннюю необратимость, вызванную наличием трения. В прямом и обратном процессах в этом случае имеется работа, затрачиваемая на трение, она превращается в теплоту.