ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.04.2024
Просмотров: 182
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Адиабатный процесс
В тепловых машинах, таких как турбина или насос, процесс протекает очень быстро и теплообмен с внешней средой очень незначителен, им можно пренебречь. Поэтому обратимым процессом в таких машинах является идеальная адиабата (изоэнтропа).
На рис. 6.24, 6.25, 6.26 изображен обратимый адиабатный процесс расширения пара 12 в Р,v-, T,s- и h,s- диаграммах.
В Р,v- диаграмме адиабата представляет собой кривую гиперболического характера с переменным показателем адиабаты "к". Необходимо отметить, что показатель адиабаты "к" для воды и пара никакого отношения к коэффициенту Пуассона cp/cv не имеет. Он рассчитывается только по параметрам обратимого адиабатного процесса вблизи какой - либо фиксированной точки по формуле
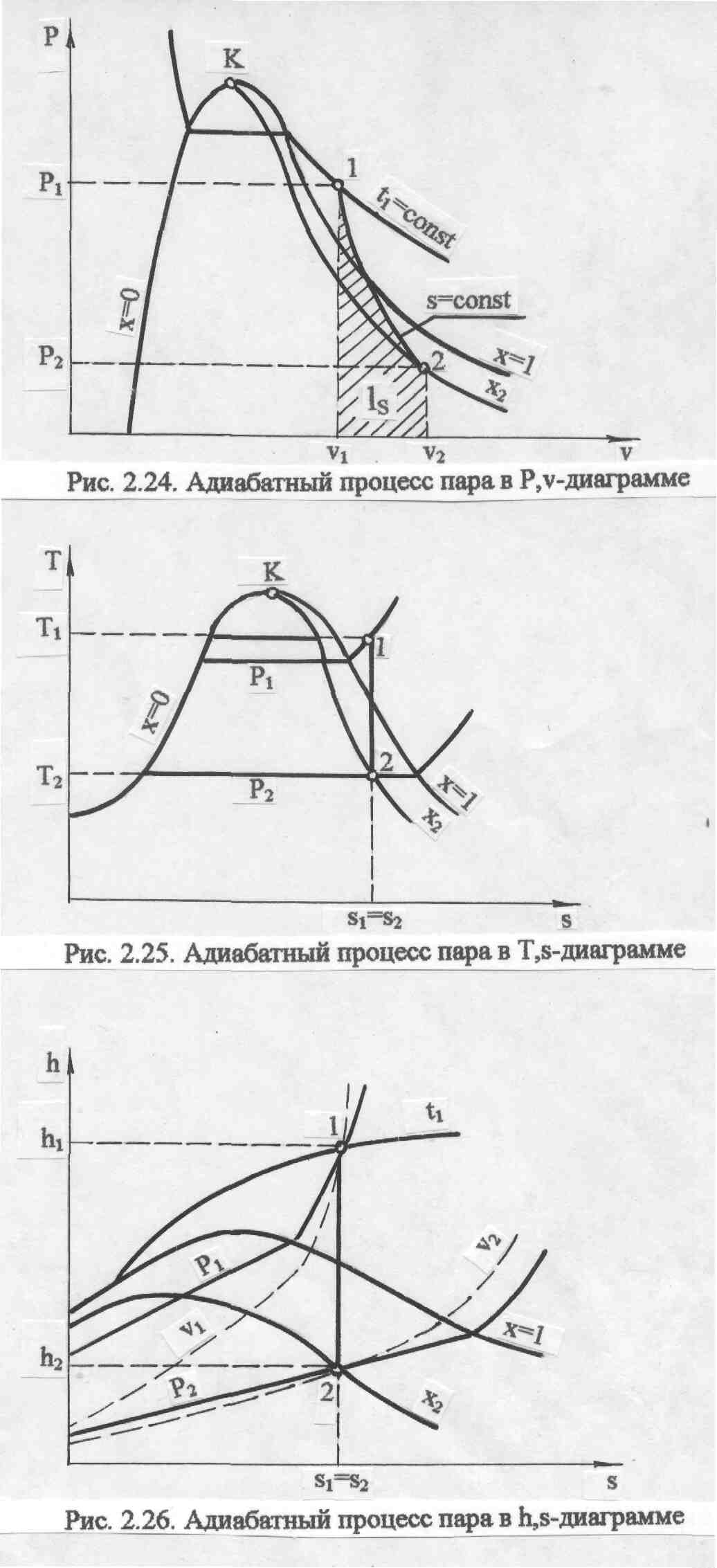

Рис. 6.24. Адиабатный процесс пара в P,v - диаграмме
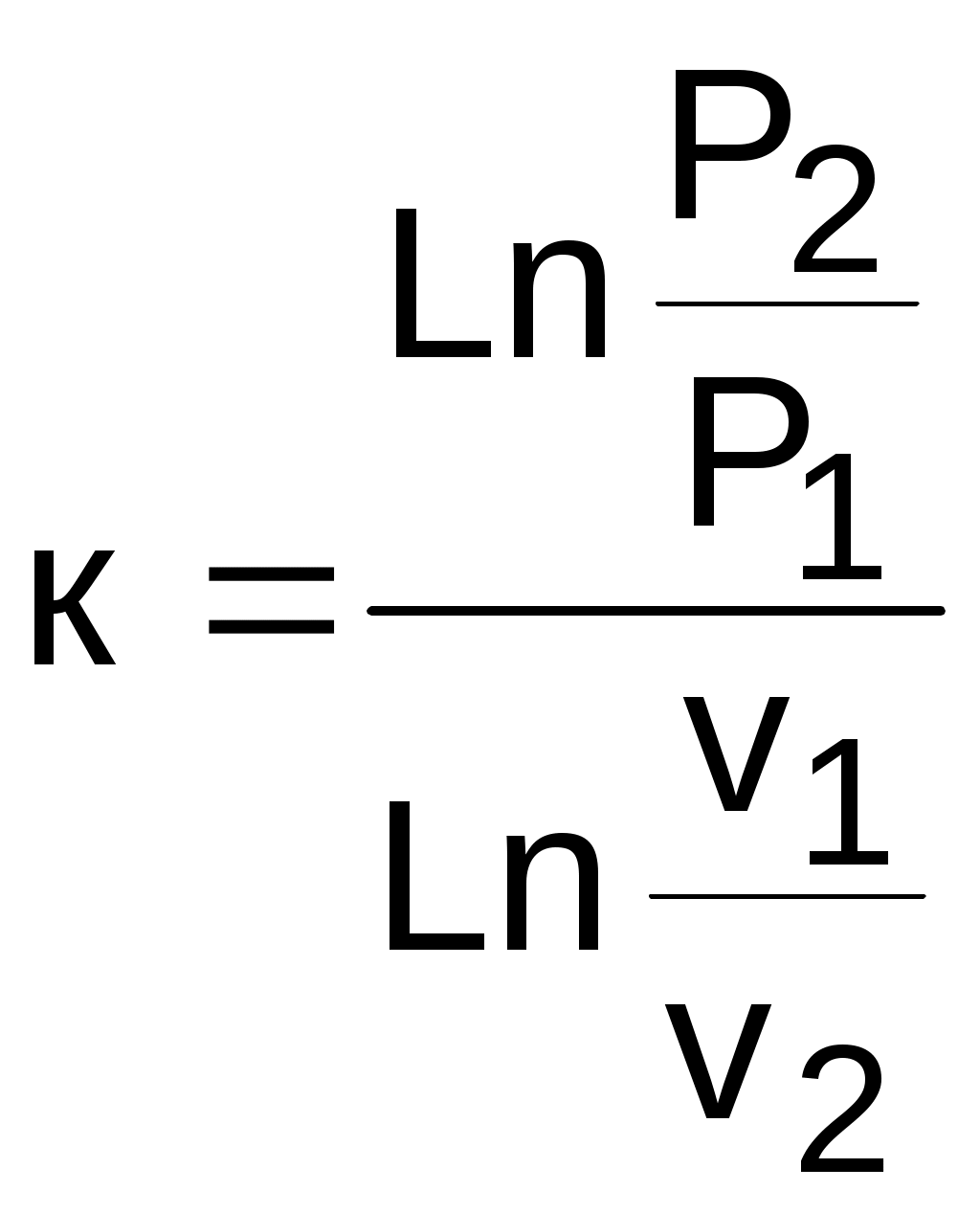 . (6.30)
. (6.30)Показателем адиабаты в расчетах процесса пользуются крайне редко ввиду того, что он – величина переменная. Его численные значения сильно отличаются друг от друга в различных точках адиабатного процесса: чем дальше расположены точки, тем больше разница. При переходе процесса из области перегретого пара в область влажного насыщенного эта разница еще больше увеличивается.
Площадь под процессом 12 в Р,v- диаграмме есть работа расширения, а поскольку qs = 0, то работа расширения адиабатного процесса равна изменению внутренней энергии с обратным знаком и может быть подсчитана как
s = u1 - u2 = (h1 - h2) - (Р1v1 - Р2v2) . (6.31)
В формуле (6.31) при расчетах следует обратить внимание на соответствие единиц измерения энтальпий и произведений Pv.
В Т,s- и h,s- диаграммах обратимый адиабатный процесс представляет вертикальную прямую (s=const – изоэнтропа). Представление энергетических характеристик (s, u) в Т,s- и h,s- диаграммах возможно с помощью дополнительных построений, но это не имеет практической ценности. В h,s- диаграмме разность энтальпий адиабатного процесса представляет работу изменения давления в потоке
о = h1 - h2 (техническая работа в турбине, насосе и т.п.). С понятием этой работы познакомимся позднее при изучении процессов теплоэнергетических установок.
Изохорный процесс
Изохорный процесс может иметь место в случае теплообмена с внешней средой водяного пара, находящегося в сосуде постоянного объема. На рис. 6.27, 6.28, 6.29 изображен изохорный процесс 12 в Р,v-, T,s-, h,s- диаграммах.
В Р,v- диаграмме изохора 12 – вертикальная прямая (рис.6.27). Работа расширения в изохорном процессе равна нулю (=Рdv, dv=0, v=0). Теплота изохорного процесса расходуется только на увеличение внутренней энергии пара:
qv = u2 - u1 = h2 - h1 -v(Р2 - Р1) . (6.32)

В диаграмме Т,s теплота qv изображается площадью под изохорным процессом 12 (рис. 6.28). Эта же площадь соответствует изменению внутренней энергии изохорного процесса. Поскольку s2 > s1, теплота и изменение внутренней энергии процесса 12 положительные.
По диаграмме h,s можно определить все необходимые параметры состояния (рис. 6.29) для расчета теплоты и изменения внутренней энергии изохорного процесса.
Изобарный процесс
На рис. 6.30, 6.31, 6.32 изображен изобарный процесс 12 в Р,v-, T,s-, h,s- диаграммах. В точке 1 этого процесса водяной пар находится в области влажного насыщенного пара, поэтому его состояние может быть задано любой парой параметров, кроме Р1 и t1, так как в этой области изобара совпадает с изотермой. Вторая точка процесса находится в области перегретого пара и состояние пара здесь определяется любой парой параметров.
В диаграмме Р,v изобара представляет горизонтальную прямую 12 (рис. 6.30), площадь под которой соответствует работе изменениия объема, определяемой по формуле
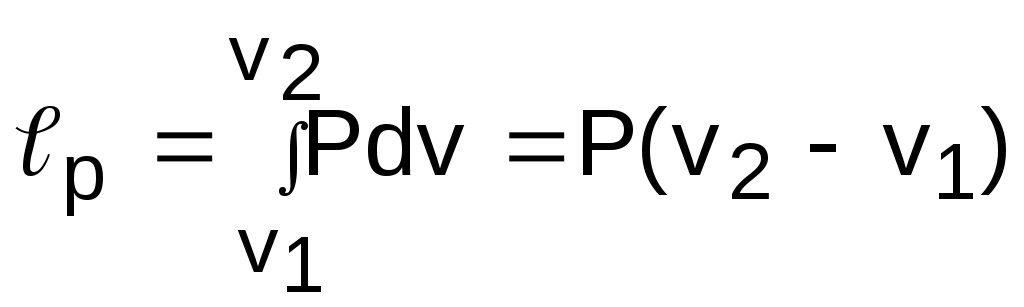 . (6.33)
. (6.33)Количество теплоты в изобарном процессе соответствует изменению энтальпии (q = dh - vdР, dР = 0, dqp = dhp) и определяется как
q

p = h2 - h1. (6.34)
В
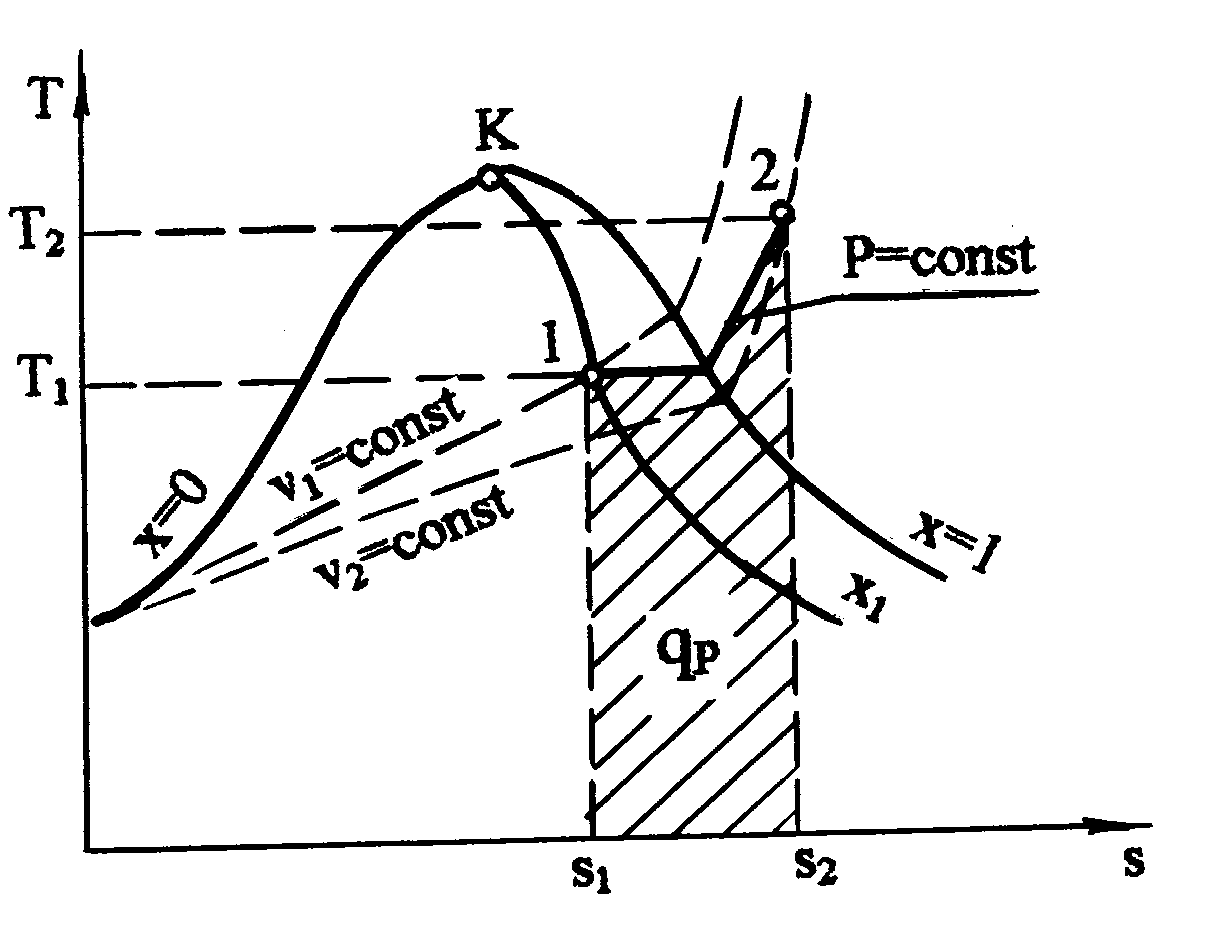
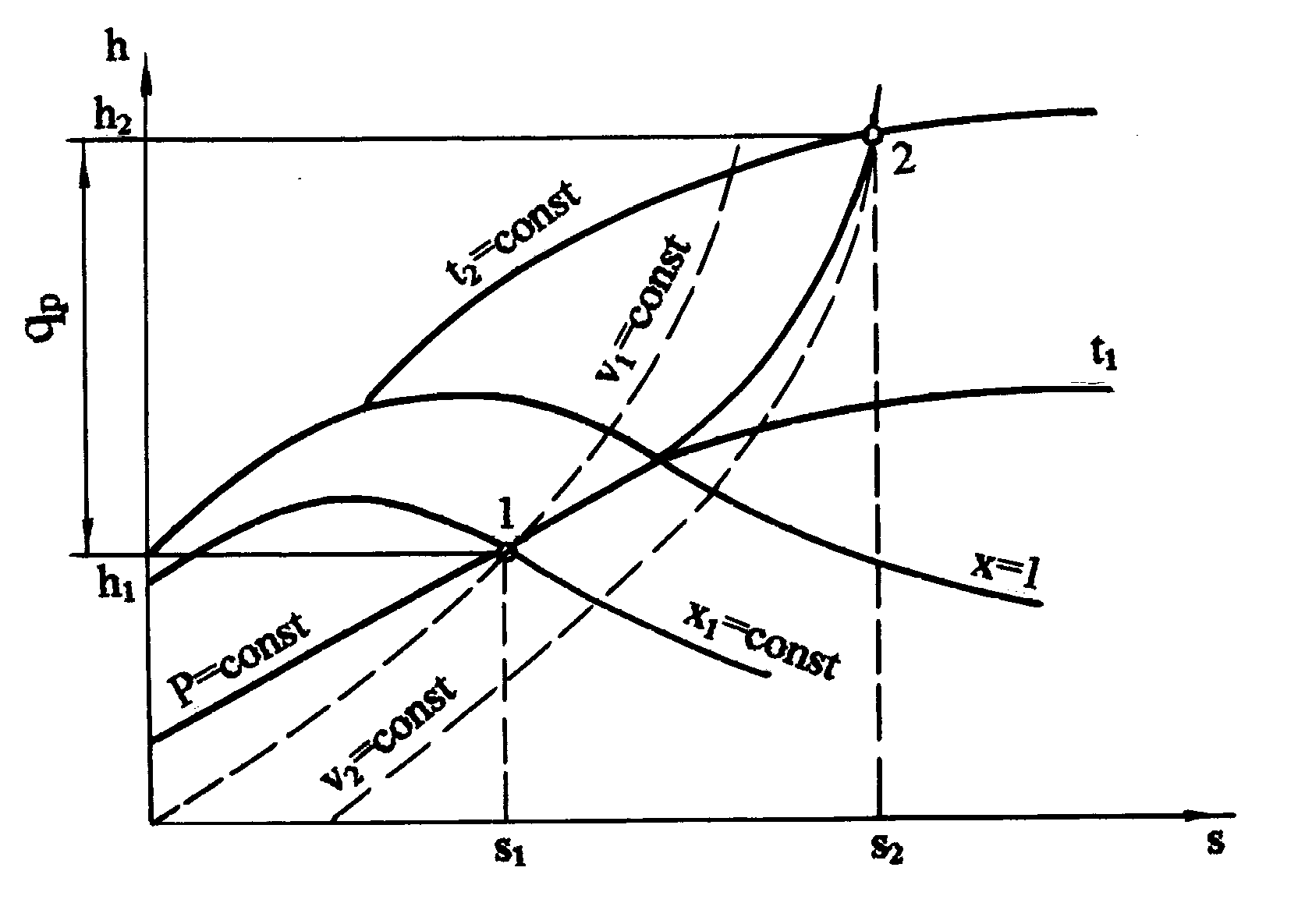
Рис. 6.31. Изобарный процесс в T, s - диаграмме
Рис. 6.32. Изобарный процесс в h, s - диаграмме
Т,s- диаграмме (рис. 6.31) теплота qp представлена площадью под процессом, в h,s- диаграмме (рис. 6.32) – отрезком прямой в виде разности ординат. Изменение внутренней энергии изобарного процесса подсчитывается по формуле
u2 - u1 = (h2 - Рv2) -(h1 - Рv1) = h2 - h1 - Р(v2 - v1) = qp - p . (6.35)
Изотермический процесс
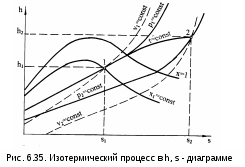
На рис. 6.33, 6.34, 6.35 изображен изотермический процесс 12 в Р,v-, T,s-, h,s- координатах. Определение параметров в начальной и конечной точках процесса аналогично предыдущим процессам.
Работа расширения изотермического процесса изображается площадью под процессом 12 в Р,v- координатах (рис. 6.33) и рассчитывается исходя из первого закона термодинамики:

т = q - (u2 - u1). (6.36)
В

Т,s- диаграмме изотерма – горизонтальная прямая. Площадь под изотермическим процессом 12 в T,s- диаграмме представляет теплоту (рис. 6.34), которая может быть подсчитана по формуле
qт = T(s2 - s1). (6.37)
В h,s- диаграмме (рис. 6.35) изотерма 12 – сложная кривая линия в области влажного пара, совпадающая с изобарой. Подсчет изменения внутренней энергии изотермического процесса ведется традиционным для водяного пара образом, через энтальпию:
u
2 - u1 = h2 - h1 - (Р2v2 - Р1v1).
7. ВЛАЖНЫЙ ВОЗДУХ
Влажный воздух – это смесь сухого воздуха и водяного пара. В воздухе при определенных условиях кроме водяного пара может находиться его жидкая (вода) или кристаллическая (лед, снег) фаза. В естественных условиях воздух всегда содержит водяной пар.
7.1. Основные характеристики влажного воздуха
Влажный воздух можно рассматривать как смесь сухого воздуха и водяного пара (жидкую и твердую фазы воды в воздухе пока считаем отсутствующими).
Используя законы для смесей газов, получим, что давление влажного воздуха равно сумме парциальных давлений сухого воздуха и водяного пара:
Р = Рв + Рп . (7.1)
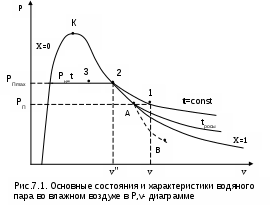
Для наглядности представления основных характеристик влажного воздуха изобразим в Р,v- диаграмме (рис.7.1) состояния водяного пара во влажном воздухе.
В качестве определяющих параметров водяного пара во влажном воздухе используются температура воздуха t
и парциальное давление водяного пара Рп.
Водяной пар во влажном воздухе может находиться в трех состояниях (рис.7.1): точка 1 – перегретый пар, точка 2 – сухой насыщенный пар, точка 3 – влажный насыщенный пар (сухой насыщенный пар плюс капельки жидкости в состоянии насыщения). Высшим пределом парциального давления водяных паров при данной температуре воздуха t является давление насыщения пара Рп max = Рн.
Абсолютная влажность – это массовое количество водяных паров в одном кубическом метре влажного воздуха. Для ее определения используется величина, обратная удельному объему водяного пара при Рп и t, =1/v (кг/м3). Действительно, по закону Дальтона водяной пар занимает весь объем смеси, а его плотность соответствует массе водяного пара в одном кубическом метре влажного воздуха.
Необходимо отметить, что абсолютная влажность воздуха характеризует содержание в воздухе только одной – паровой фазы воды.
Относительная влажность – это отношение абсолютной влажности к максимально возможной влажности воздуха при данной температуре:
 , (7.2)
, (7.2)где " и v" – максимальная абсолютная влажность воздуха и удельный объем сухого насыщенного водяного пара при данной температуре t.
Относительная влажность воздуха характеризует потенциальную возможность воздуха испарять влагу и забирать в себя пар из окружающей среды при данной температуре.
Максимальное содержание пара в воздухе соответствует состоянию точки 2 в Р,v- диаграмме (см. рис.7.1), где пар сухой насыщенный. При переходе в область влажного пара при данной температуре t (точка 3) в воздухе количество сухого насыщенного пара остается постоянным (такое же, как в точке 2) (для паровой фазы воды в этом случае удельный объем остается неизменным, v"=const, и минимально возможным при данной температуре воздуха), только к нему добавляются капельки воды в состоянии насыщения.
Различают 3 состояния влажного воздуха.
1. Ненасыщенный влажный воздух – <100 %, Рп<Рн, <", водяной пар во влажном воздухе в виде перегретого пара (точка 1).
2. Насыщенный влажный воздух – =100 %, Рп=Рн, =", водяной пар во влажном воздухе в виде сухого насыщенного пара (точка 2).
3. Перенасыщенный влажный воздух– =100 %, Рп=Рн, =", кроме сухого насыщенного пара в воздухе находятся капельки воды в состоянии насыщения или льда, снега (точка 3 при наличии капелек воды).
В технике используется такая характеристика влажного воздуха, как температураточки росы. Это такая температура, начиная с которой при охлаждении влажного воздуха при постоянном давлении из него начинается выпадение капелек воды (соответствует температуре точки А процесса 1А, рис. 7.1). При снижении температуры воздуха ниже температуры точки росы при постоянном давлении всей смеси и постоянном содержании в ней H2О (процесс АВ) парциальное давление водяного пара уменьшается (Рвп<Рп), количество сухого насыщенного пара уменьшается, а количество капелек воды увеличивается. В этом случае в P,v- диаграмме процесс АВ пойдет в области влажного пара с уменьшением степени сухости по мере снижения температуры.
7.2. Характеристики атмосферного влажного воздуха
При температурах атмосферного воздуха 0-50 оС парциальное давление водяного пара очень мало (0,006-0,07 бар), что позволяет применить к перегретому и сухому насыщенному водяному пару уравнение идеального газа:
Рпv = RT, (7.3)
Рнv" = RT, (7.4)
где Рп, Рн и v, v" – парциальные давления и удельные объемы для перегретого и сухого насыщенного водяного пара при температуре Т.
Разделив эти выражения друг на друга, получим расчетное выражение относительной влажности воздуха через парциальные давления водяного пара:
 . (7.5)
. (7.5)Молярная масса атмосферного влажного воздуха определяется по уравнению для смеси газов:
= rвв + rпп, (7.6)
где rв, rп – объемные доли сухого воздуха и водяного пара,

