Файл: Методические указания по выполнению контрольной работы для студентов заочной формы обучения, осваивающих профессиональный модуль пм. 01 Выполнение работ по созданию геодезических, нивелирных сетей и сетей специального назначения.doc

2 ОПРЕДЕЛЕНИЕ ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ
Контрольная работа выполняется по одному из вариантов, номер которого для каждого студента определяется по двум последним цифрам его личного шифра и количеству букв в его фамилии.

Если две последние цифры (N) его шифра от 1 до 30, то для определения варианта применяется следующая формула: № = N+K, где K – количество букв в его фамилии.

Если две последние цифры (N) его шифра от 31 до 60, то для определения варианта применяется следующая формула: № = (N-30)+K, где K – количество букв в его фамилии.

Если две последние цифры (N) его шифра от 61 до 90, то для определения варианта применяется следующая формула: № = (N-60)+K, где K – количество букв в его фамилии.

Если две последние цифры (N) его шифра от 91 до 100, то для определения варианта применяется следующая формула: № = (N-90)+K, где K – количество букв в его фамилии.

Например, личный шифр студента Иванова И.И. обозначен цифрами 7499, тогда вариант контрольного задания определяется следующим образом: устанавливаются две последние цифры – это 99, затем находится число для вычитания – это 90, количество букв в его фамилии «Иванов» - 6 ; далее производится простое арифметическое действие (99–90)+6 = 15 и устанавливается номер варианта; в данном примере - это вариант № 15.

Самостоятельная замена или произвольный выбор студентом варианта контрольного задания не допускается.
3 МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ

КОНТРОЛЬНОЙ РАБОТЫ

3.1 Введение

Обязательным видом самостоятельной работы студентов заочной формы обучения, изучающих МДК 01.02 «Методы математической обработки результатов полевых геодезических измерений и оценка их точности», является домашняя письменная контрольная работа, которая одновременно выполняет функции средства приобретения и углубления знаний, а также их контроля и оценки. Контрольная работа является неотъемлемой частью учебной программы, выполняется студентом в межсессионный период и представляется к рецензированию в сроки, установленные графиком учебного процесса.

Выполнение контрольной работы демонстрирует способность студентов применить умения и знания при уравнивании полигонометрического хода двухгрупповым способом по МНК.

---

Завершенная контрольная работа представляет собой выполненные расчеты по уравниванию разомкнутого полигонометрического хода, оформленные в виде таблиц.

Контрольная работа по МДК 01.02 выполняется после предварительного ознакомления с требованиями ФГОС СПО к результатам освоения профессионального модуля ПМ.01«Выполнение работ по созданию геодезических, нивелирных сетей и сетей специального назначения», рабочей программой по данному модулю, изучения рекомендованных информационно-библиографических ресурсов.

Выполнение контрольной работы состоит из следующих этапов:

1) ознакомление с содержанием МДК 01.02 «Методы математической обработки результатов полевых геодезических измерений и оценка их точности»;

2) определение варианта заданий контрольной работы;

3) подбор и изучение информационно-библиографических ресурсов (учебников и учебных пособий, различных инструкций, Интернет-материалов и др.);

4) систематизация материала;

5) изучение порядка выполнения каждого задания контрольной работы;

6) консультация у преподавателя, преподающего дисциплину;

7) вычисления, их проверка, окончательное оформление работы;

8) представление выполненной работы методисту заочного отделения;

9) оценка и рецензия представленной контрольной работы преподавателем;

10) устранение автором работы указанных в рецензии замечаний;

11) подготовка к устному собеседованию по содержанию каждого задания контрольной работы.

Написанию контрольной работы должен предшествовать активный поиск информационно-библиографических ресурсов по избранной теме.

3.2 Указания по выполнению контрольной работы
Способы уравнивания полигонометрических ходов

Полигонометрией называют метод определения положения геодезических пунктов путем построения на местности полигонометрического хода (ломанной линии) или систем ходов (полигонометрическая сеть), в которых измеряются все углы и стороны. Полигонометрические ходы опираются на исходные пункты более высокого класса. Они могут быть разомкнутыми и замкнутыми. Если ход по форме близок к прямой линии, то его называют вытянутым, в противном случае – изогнутым.

Задача уравнивания возникает в том случае, когда имеются избыточные измерения.

Установим, сколько избыточных измерений будет в полигонометрическом ходе, опирающемся на исходные пункты

---

Т_н и Т_к и исходные направления _ни _к.

Число избыточных измерений может быть подсчитано по формуле:

, (1)

где - число всех измерений;

- число необходимых измерений (определяемых неизвестных).

При проложении полигонометрического хода измеряют n сторон и n+1 углов, т.е производят всего измерений n^/ =2n+1. Неизвестными, подлежащими определению в ходе, являются координаты его вершин. Всего пунктов в ходе n+1, но координаты двух из них известны, следовательно, надо определить координаты n+1-2=n-1 пунктов. Для каждого пункта необходимо найти x и y – два неизвестных. Тогда общее число неизвестных будет равно k=2(n-1). Подставим найденные значения и в формулу (1), получим:

,

т.е. будет три избыточных измерения.

Полигонометрические сети уравниваются двумя способами: строгим, когда уравнивание производится под условием (pvv)=min и нестрогим, раздельным, когда сначала уравниваются углы, а затем раздельно между собой приращения координат.

При строгом уравнивании по методу наименьших квадратов (МНК), возникает вопрос, каким способом производить уравнивание: коррелатным или параметрическим?

При уравнивании параметрическим способом число нормальных уравнений равно числу неизвестных, в данном случае 2(n-1) (всего пунктов n+1, но координаты двух из них известны, следовательно, надо определить координаты n+1-2=n-1 пунктов), т.е. чем длиннее ход, тем больше нормальных уравнений.

При уравнивании коррелатным способом число нормальных уравнений определяется числом условий, а число условий – числом избыточных измерений r=n^/-k =3. Следовательно, в полигонометрическом ходе независимо от числа линий и его длины будет только три нормальных уравнения. Т.о. полигонометрию целесообразно уравнивать коррелатным способом. Однако объем вычислений и в этом способе уравнивания остается значительным. Поэтому используют все возможные упрощения, вытекающие из самого способа (двухгрупповой, трехгрупповой способы уравнивания).

---

ЗАДАНИЕ

Уравнивание полигонометрического хода 4 класса двухгрупповым

способом по методу наименьших квадратов (МНК)

Три избыточных измерения в полигонометрическом ходе приводят, как было установлено, к возникновению трех условий и трех условных уравнений.

Первое условие возникает из связи углов поворота полигонометрического хода с начальным _ни конечным _к дирекционными углами. Оно может быть выражено так:

, (2)

где - уравненные значения углов, равные измеренным углам плюс поправки : .

В зависимости от ориентации хода относительно исходных направлений в последнем слагаемом формулы (2) множитель бывает не только (n+1), но может иметь и другие значения, например, (n-2).

Второе и третье условия вытекают из связи приращений координат с исходными начальными и конечными координатами:

, , (3)

где , - уравненные значения приращений координат, равные

вычисленным приращениям координат , плюс поправки:

, .

От данных трех условий перейдем к трем условным уравнениям поправок: азимутальному (угловому) и двум координатным:

---

;

; (4)

,

где - невязка по измеренным углам поворота полигонометрического

хода,

, - невязки в приращения координат, штрихи у невязок обозначают, что эти невязки получены по приращениям, вычисленным по измеренным углам (без их предварительного уравнивания).

Поправки и - поправки к величинам зависимым, т.к. приращения координат не измерялись в поле, а вычислялись по одним м тем же углам и линиям в камеральных условиях. Поэтому условные уравнения (4) необходимо преобразовать так, чтобы вместо поправок и в них фигурировали поправки в углы и линии .

После преобразований условные уравнения поправок (4) примут вид:



(5)

.

Для решения данной системы условных уравнений введем центральные координаты. Начало координат выгодно перенести в точку с координатами x_ц и y_ц (центр тяжести), которые вычисляются по формулам:

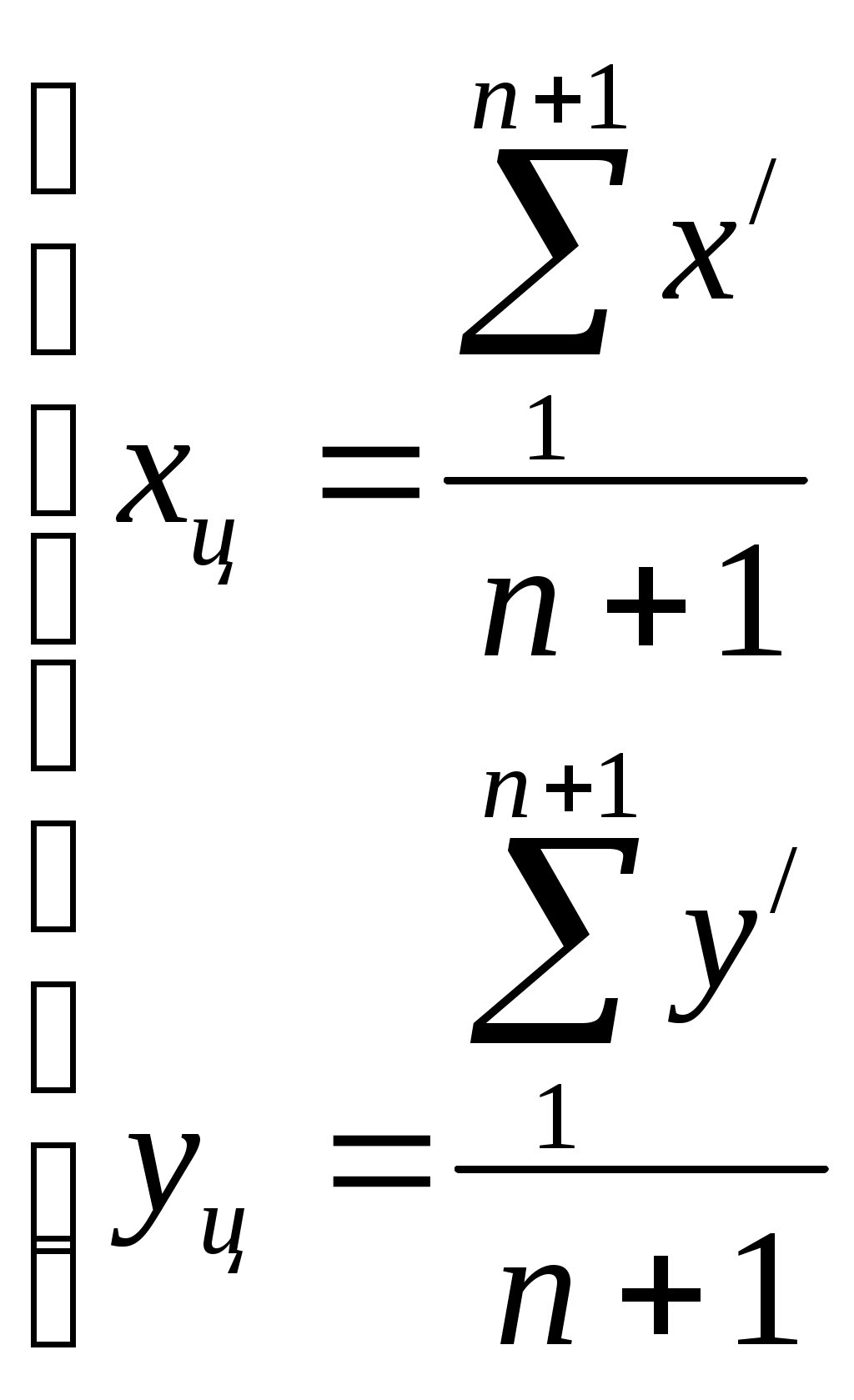(6)

где x^/ и

---