ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.04.2024
Просмотров: 40
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
с=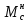 составляет
составляет 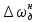 =0.8 . Поскольку
=0.8 . Поскольку 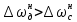 , то разомкнутая система должна быть заменена замкнутой.
, то разомкнутая система должна быть заменена замкнутой.
3.2 Исходная система в замкнутом состоянии
На основе формулы (3.1) в статическом режиме (р = 0), можно записать уравнение статики:
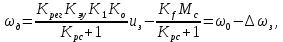 (3.3)
(3.3)
где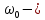 скорость холостого хода двигателя;
скорость холостого хода двигателя;
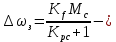 статическая ошибка в замкнутой системе.
статическая ошибка в замкнутой системе.
В соответствии с заданием на проектирование должно выполняться условие:
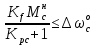 (3.4)
(3.4)
Используя знак равенства в формуле (3.4), можно записать формулу для расчета требуемого значения коэффициента передачи разомкнутой системы:
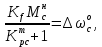
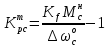 (3.5)
(3.5)
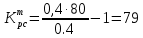
Поскольку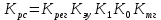 , то
, то
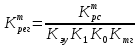 (3.6)
(3.6)
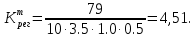
4 Анализ устойчивости исходной системы алгебраическим критерием Гурвица
Используя формулу (2.25) или (2.27), можно записать характеристическое уравнение исходной замкнутой системы:
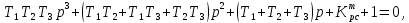
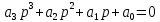 , (4.1)
, (4.1)
где а3 =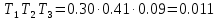
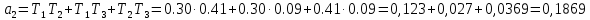
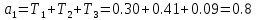
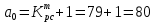
Главный определитель Гурвица:
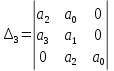
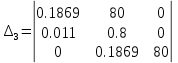
Проверка условий устойчивости:
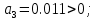
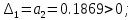
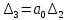 поскольку
поскольку 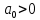 , можно записать:
, можно записать:
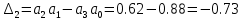
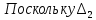
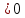 и, следовательно,
и, следовательно, 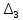
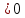 , то в соответствии с критерием Гурвица исходная система является неустойчивой.
, то в соответствии с критерием Гурвица исходная система является неустойчивой.
Граничное значение коэффициента передачи разомкнутой системы, можно найти из условия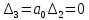 , поскольку
, поскольку 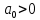 , то можно записать
, то можно записать
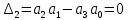
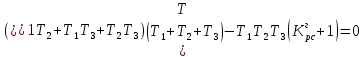
Граничное значение коэффициента передачи разомкнутой системы находится по формуле:
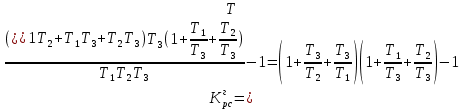 (4.2)
(4.2)
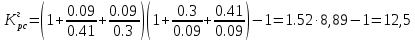
Поскольку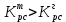 , то это подтверждает вывод о неустойчивости исходной системы.
, то это подтверждает вывод о неустойчивости исходной системы.
5 Коррекция динамических свойств системы
5.1 Расчет параметров корректирующего устройства
На рисунке 5.1 приведена схема регулятора, на основе усилителя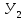 , выполняющая функцию коррекции динамических свойств исходной системы.
, выполняющая функцию коррекции динамических свойств исходной системы.
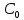
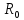
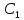

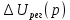
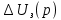
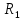
 2
2
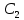
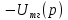
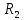
Рисунок 5.1 Схема корректирующего устройства
Пусть: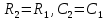
Передаточная функция регулятора рассчитывается по формуле:
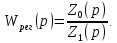 (5.1)
(5.1)
Передаточная функция регулятора рассчитывается по формуле:
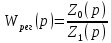 (5.1)
(5.1)
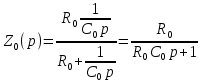 ;
;
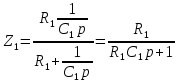 ;
;
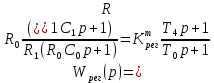 , (5.2)
, (5.2)
где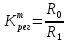 – требуемое значение коэффициента передачи регулятора.
– требуемое значение коэффициента передачи регулятора.
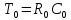 ,
, 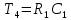 - постоянная времени.
- постоянная времени.
В соответствии с теорией управления, можно принять:
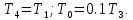 (5.3)
(5.3)
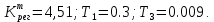
С учетом формул (5.2) и (5.3) можно записать:

Пусть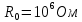 , тогда:
, тогда:
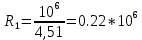
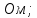
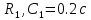 ;
; 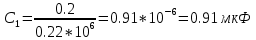 .
.
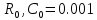
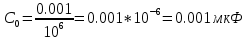 .
.
5.2 Устойчивость скорректированной САУ
На основе рисунка 2.7 с учётом формул (5.2 и 5.3) можно построить структурную схему скорректированной системы (рисунок 5.2).

Рисунок 5.2 Структурная схема скорректированной системы
Пусть возмущающее воздействие не изменяется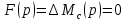 , поэтому на основе рисунка 5.2 с учетом
, поэтому на основе рисунка 5.2 с учетом 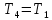 можно записать передаточную функцию замкнутой скорректированной системы по управляющему воздействию:
можно записать передаточную функцию замкнутой скорректированной системы по управляющему воздействию:
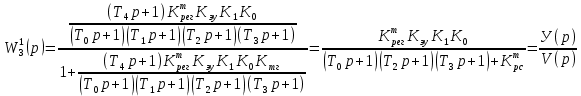 (5.4)
(5.4)
Изображение Лапласа выходного сигнала:
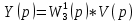 (5.5)
(5.5)
Пусть входной сигнал не изменяется т.е.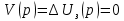 , тогда на основе рисунка 5.2 можно записать скорректированную передаточную функцию по возмущающему воздействию:
, тогда на основе рисунка 5.2 можно записать скорректированную передаточную функцию по возмущающему воздействию:
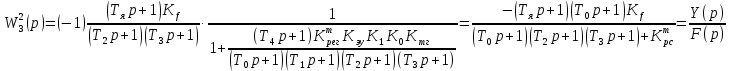 (5.6)
(5.6)
Изображение Лапласа выходного сигнала:
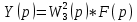 (5.7)
(5.7)
На основе принципа суперпозиции с учётом формул (5.4) – (5.7) можно записать изображение Лапласа выходного сигнала при двух входных воздействиях:
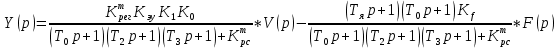 (5.8)
(5.8)
Используя передаточную функцию (5.4) или (5.6), можно записать уравнение замкнутой скорректированной системы:
 (5.9)
(5.9)
где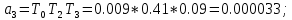
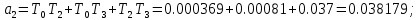
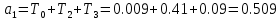 ;
;
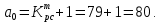
Главный определитель Гурвица:

Проверка условий устойчивости:
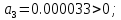
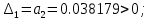
 , поскольку
, поскольку
 , можно записать:
, можно записать:
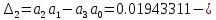
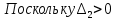 и, следовательно,
и, следовательно, 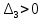 , то в соответствии с критерием Гурвица скорректированная система является устойчивой.
, то в соответствии с критерием Гурвица скорректированная система является устойчивой.
Граничное значение коэффициента передачи разомкнутой системы, можно найти из условия , поскольку
, поскольку  , то можно записать
, то можно записать

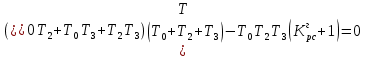
Граничное значение коэффициента передачи разомкнутой системы находится по формуле:
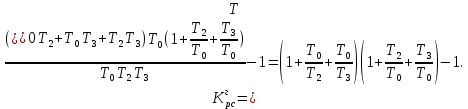
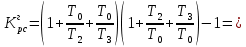
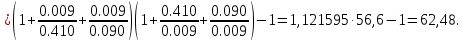
Поскольку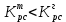 , то это подтверждает вывод об устойчивости скорректированной системы.
, то это подтверждает вывод об устойчивости скорректированной системы.
6 Показатели качества переходного процесса
На рисунке 6.1 представлена структурная схема скорректированной САР. На основе модели в среде MATLAB (рисунок 6.1) можно получить график переходного процесса в скорректированной САР, приведенный на рисунке 6.2.
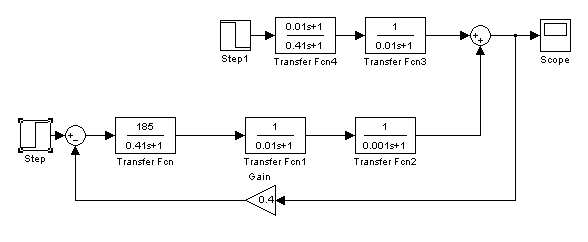
Рисунок 6.1 –Модель структурной схемы скорректированной САР
в среде MATLAB
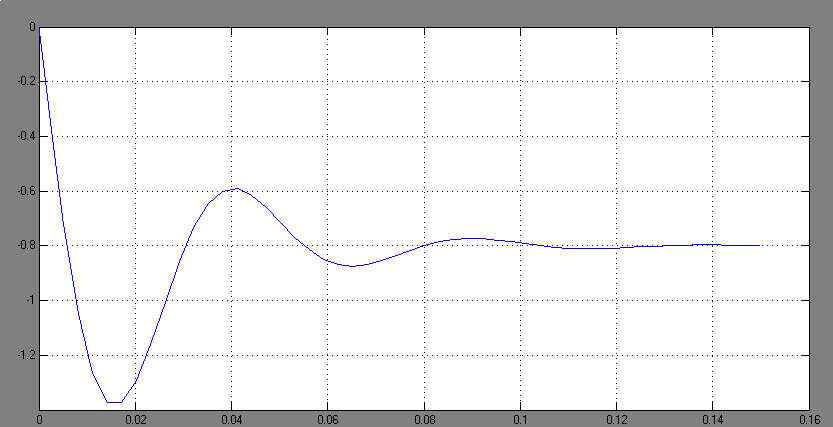
Рисунок 6.2 - График переходного процесса в скорректированной САР
по возмущающему воздействию
В соответствии с рисунок 6.2 определим показатели качества переходного процесса:
1) Время переходного процесса tп.п.=0.09 с;
2) Перерегулирование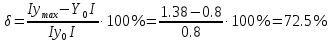 ;
;
3) Вид переходного процесса – колебательный;
4) Период собственных колебаний Тк= 0.08 - 0.03= 0.05с;
5) Частота колебаний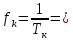 1/0.05= 20
1/0.05= 20 
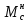 составляет
составляет 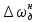 =0.8 . Поскольку
=0.8 . Поскольку 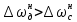 , то разомкнутая система должна быть заменена замкнутой.
, то разомкнутая система должна быть заменена замкнутой.3.2 Исходная система в замкнутом состоянии
На основе формулы (3.1) в статическом режиме (р = 0), можно записать уравнение статики:
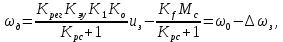 (3.3)
(3.3)где
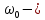 скорость холостого хода двигателя;
скорость холостого хода двигателя;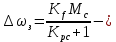 статическая ошибка в замкнутой системе.
статическая ошибка в замкнутой системе.В соответствии с заданием на проектирование должно выполняться условие:
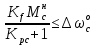 (3.4)
(3.4)Используя знак равенства в формуле (3.4), можно записать формулу для расчета требуемого значения коэффициента передачи разомкнутой системы:
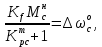
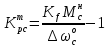 (3.5)
(3.5)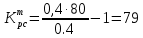
Поскольку
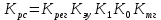 , то
, то 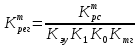 (3.6)
(3.6)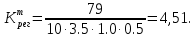
4 Анализ устойчивости исходной системы алгебраическим критерием Гурвица
Используя формулу (2.25) или (2.27), можно записать характеристическое уравнение исходной замкнутой системы:
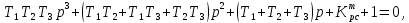
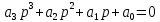 , (4.1)
, (4.1)где а3 =
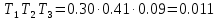
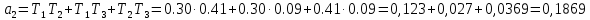
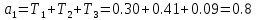
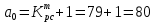
Главный определитель Гурвица:
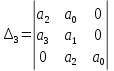
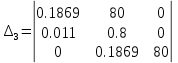
Проверка условий устойчивости:
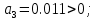
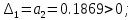
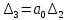 поскольку
поскольку 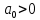 , можно записать:
, можно записать: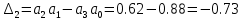
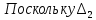
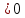 и, следовательно,
и, следовательно, 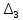
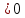 , то в соответствии с критерием Гурвица исходная система является неустойчивой.
, то в соответствии с критерием Гурвица исходная система является неустойчивой.Граничное значение коэффициента передачи разомкнутой системы, можно найти из условия
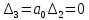 , поскольку
, поскольку 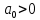 , то можно записать
, то можно записать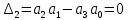
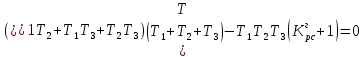
Граничное значение коэффициента передачи разомкнутой системы находится по формуле:
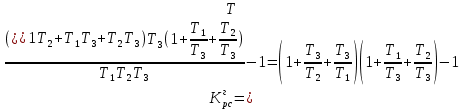 (4.2)
(4.2)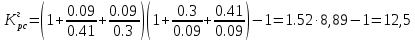
Поскольку
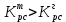 , то это подтверждает вывод о неустойчивости исходной системы.
, то это подтверждает вывод о неустойчивости исходной системы.5 Коррекция динамических свойств системы
5.1 Расчет параметров корректирующего устройства
На рисунке 5.1 приведена схема регулятора, на основе усилителя
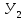 , выполняющая функцию коррекции динамических свойств исходной системы.
, выполняющая функцию коррекции динамических свойств исходной системы.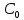
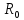
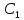

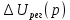
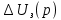
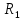
 2
2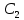
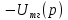
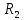
Рисунок 5.1 Схема корректирующего устройства
Пусть:
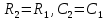
Передаточная функция регулятора рассчитывается по формуле:
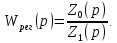 (5.1)
(5.1)Передаточная функция регулятора рассчитывается по формуле:
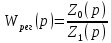 (5.1)
(5.1)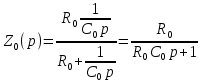 ;
;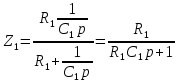 ;
; 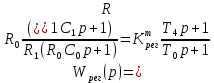 , (5.2)
, (5.2)где
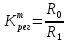 – требуемое значение коэффициента передачи регулятора.
– требуемое значение коэффициента передачи регулятора.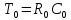 ,
, 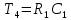 - постоянная времени.
- постоянная времени.В соответствии с теорией управления, можно принять:
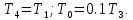 (5.3)
(5.3)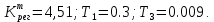
С учетом формул (5.2) и (5.3) можно записать:

Пусть
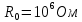 , тогда:
, тогда: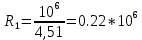
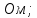
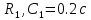 ;
; 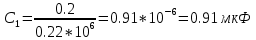 .
.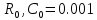
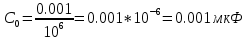 .
.5.2 Устойчивость скорректированной САУ
На основе рисунка 2.7 с учётом формул (5.2 и 5.3) можно построить структурную схему скорректированной системы (рисунок 5.2).

Рисунок 5.2 Структурная схема скорректированной системы
Пусть возмущающее воздействие не изменяется
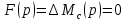 , поэтому на основе рисунка 5.2 с учетом
, поэтому на основе рисунка 5.2 с учетом 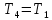 можно записать передаточную функцию замкнутой скорректированной системы по управляющему воздействию:
можно записать передаточную функцию замкнутой скорректированной системы по управляющему воздействию: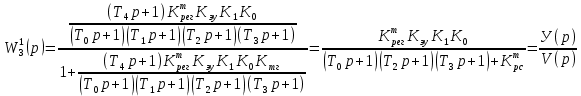 (5.4)
(5.4)Изображение Лапласа выходного сигнала:
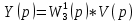 (5.5)
(5.5)Пусть входной сигнал не изменяется т.е.
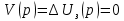 , тогда на основе рисунка 5.2 можно записать скорректированную передаточную функцию по возмущающему воздействию:
, тогда на основе рисунка 5.2 можно записать скорректированную передаточную функцию по возмущающему воздействию: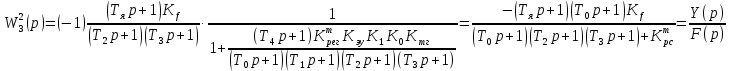 (5.6)
(5.6)Изображение Лапласа выходного сигнала:
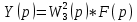 (5.7)
(5.7)На основе принципа суперпозиции с учётом формул (5.4) – (5.7) можно записать изображение Лапласа выходного сигнала при двух входных воздействиях:
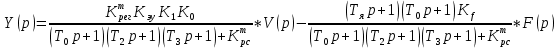 (5.8)
(5.8)Используя передаточную функцию (5.4) или (5.6), можно записать уравнение замкнутой скорректированной системы:
 (5.9)
(5.9)где
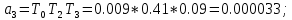
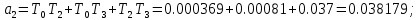
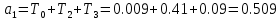 ;
;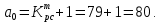
Главный определитель Гурвица:

Проверка условий устойчивости:
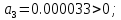
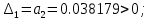
 , поскольку
, поскольку
 , можно записать:
, можно записать: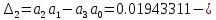
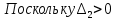 и, следовательно,
и, следовательно, 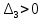 , то в соответствии с критерием Гурвица скорректированная система является устойчивой.
, то в соответствии с критерием Гурвица скорректированная система является устойчивой.Граничное значение коэффициента передачи разомкнутой системы, можно найти из условия
 , поскольку
, поскольку  , то можно записать
, то можно записать
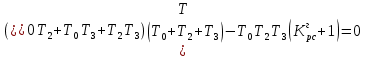
Граничное значение коэффициента передачи разомкнутой системы находится по формуле:
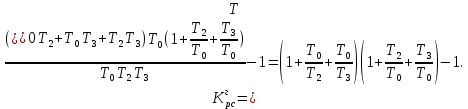
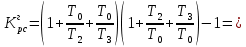
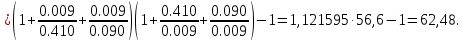
Поскольку
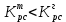 , то это подтверждает вывод об устойчивости скорректированной системы.
, то это подтверждает вывод об устойчивости скорректированной системы.6 Показатели качества переходного процесса
На рисунке 6.1 представлена структурная схема скорректированной САР. На основе модели в среде MATLAB (рисунок 6.1) можно получить график переходного процесса в скорректированной САР, приведенный на рисунке 6.2.

Рисунок 6.1 –Модель структурной схемы скорректированной САР
в среде MATLAB

Рисунок 6.2 - График переходного процесса в скорректированной САР
по возмущающему воздействию
В соответствии с рисунок 6.2 определим показатели качества переходного процесса:
1) Время переходного процесса tп.п.=0.09 с;
2) Перерегулирование
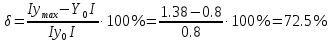 ;
;3) Вид переходного процесса – колебательный;
4) Период собственных колебаний Тк= 0.08 - 0.03= 0.05с;
5) Частота колебаний
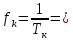 1/0.05= 20
1/0.05= 20 

