Файл: Vii неустановившаяся фильтрация упругой жидкости в упругой пористой среде.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.04.2024
Просмотров: 14
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, (7.44)
где
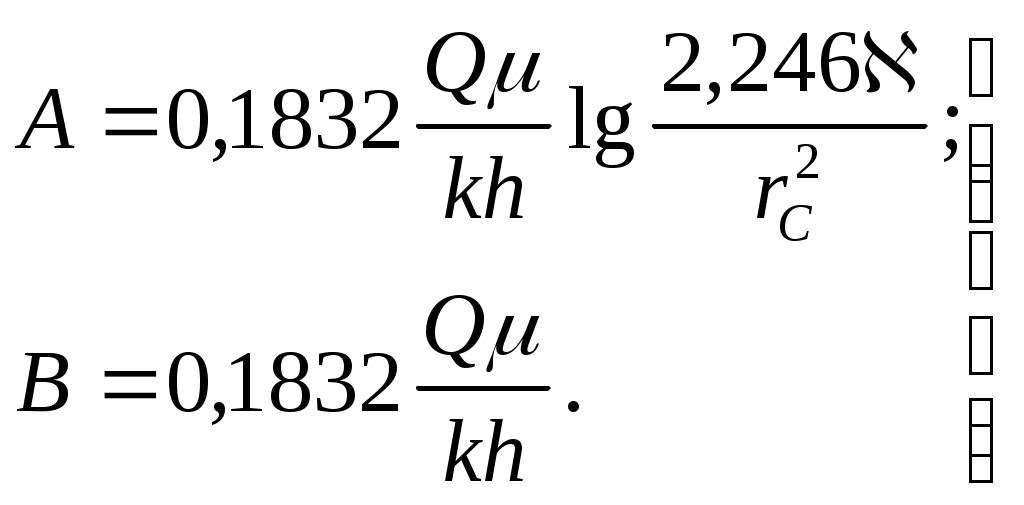 (7.45)
(7.45)
Как видно из формул (7.43) и (7.44) изменение (снижение) забойного давления в пущенной с постоянным дебитом Q скважине оказывается линейной функцией логарифма времени. Следовательно, эти формулы можно рассматривать как уравнение графика изменения забойного давления после пуска скважины в эксплуатацию.
Рассмотрим теперь кривую восстановления забойного давления, т.е. рост забойного давления после мгновенной остановки скважины. Будем считать, что до остановки скважина длительное время работала с постоянным дебитом Q и вокруг нее в пласте имело место установившееся распределение пластового давления в соответствии с формулой (3.25)
 ,
,
т.е. пьезометрическая линия является кривой логарифмического типа.
Изменение забойного давления после мгновенной остановки скважины можно определить, используя принцип суперпозиции:
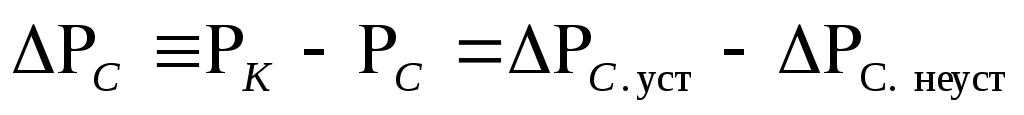 , (7.46)
, (7.46)
где С. уст – депрессия на пласт при установившейся работе добывающей скважины с дебитом Q:

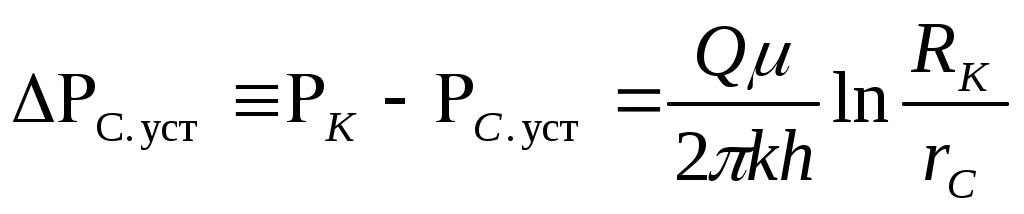 ; (7.47)
; (7.47)
С. неуст – изменение давления на забое воображаемой нагнетательной скважины, пущенной в момент t=0 с расходом Q:
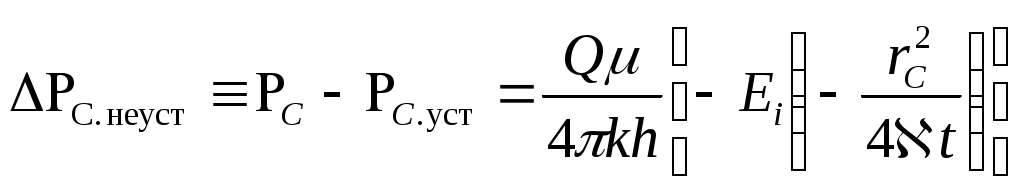 . (7.48)
. (7.48)
Так как уст величина постоянная (от времени не зависит), то изменение забойного давления С будет определяться по формуле (7.48), которая совпадает с формулами (7.43) и (7.44).
Обработка кривых восстановления забойного давления и определения по ним коллекторских свойств пласта проводятся следующим образом. Снятую скважинным манометром кривую восстановления забойного давления после остановки скважины перестраивают в координатах (С, lg t). По прямому участку этой кривой (рис.50) находится отрезок, отсекаемый ее продолжением на оси С
(отрезок А), и тангенс угла наклона этой прямой к оси абсцисс (B=tg ). Затем с помощью второго равенства (7.45) определяется параметр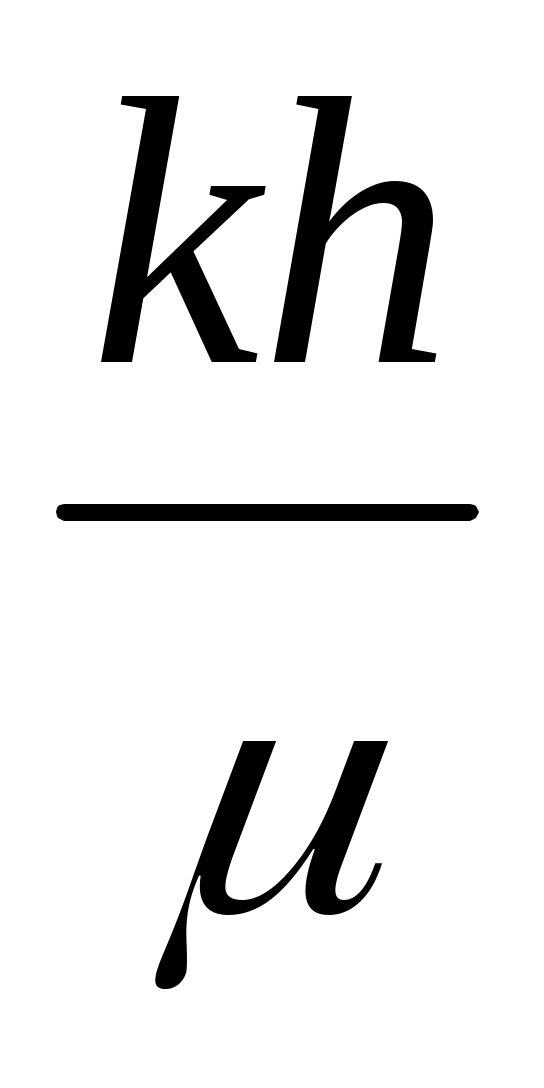 , называемый гидропроводностью пласта, т.е.
, называемый гидропроводностью пласта, т.е.

 . (7.49)
. (7.49)
Если известны вязкость жидкости в пластовых условиях и толщина пласта h, то из последней формулы находится коэффициент проницаемости пласта
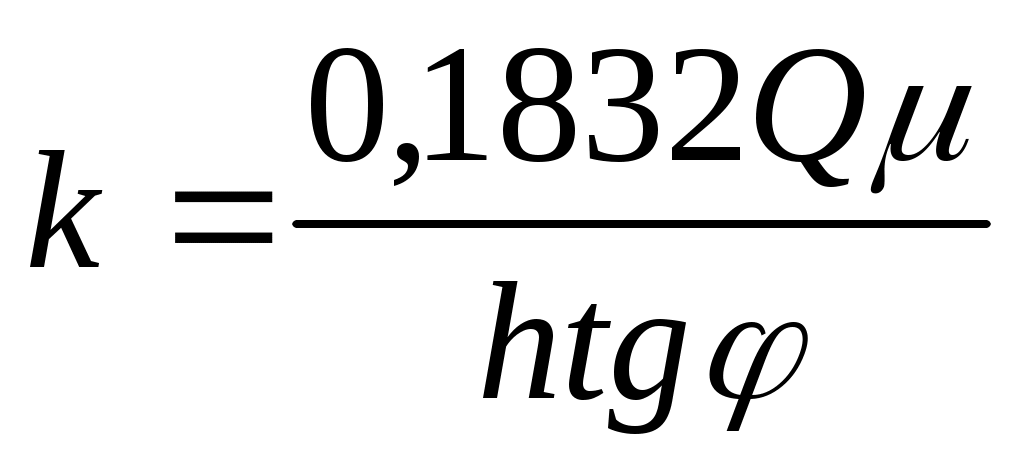 . (7.50)
. (7.50)
Далее по известному угловому коэффициенту B=tg и радиусу скважины из первого равенства (7.45)
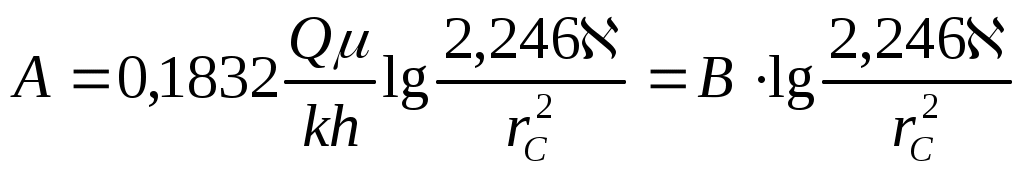
можно определить коэффициент пьезопроводности пласта

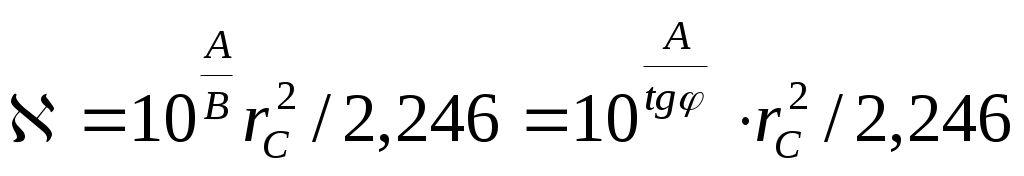 . (7.51)
. (7.51)
Отметим, что область применения указанных простых приемов интерпретации результатов исследования нефтяных скважин ограничивается условиями, при которых справедлива формула (7.37), а именно:
скважина рассматривается как источник постоянной интенсивности в бесконечном однородном пласте, и возможна мгновенная остановка притока флюида в скважину.
Г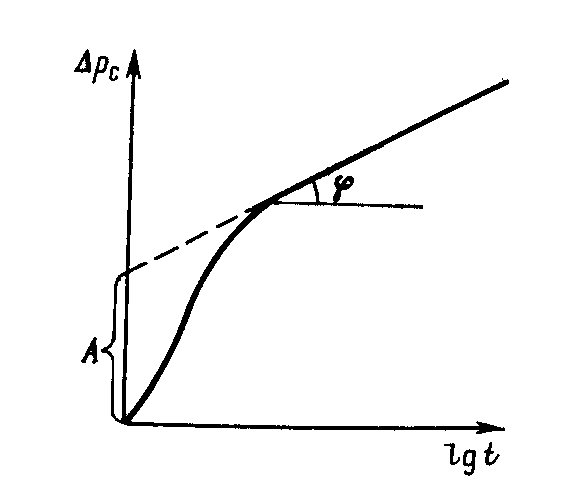 рафик, построенный по результатам реальных промысловых исследований скважин, принимает форму прямой не сразу. На форму начальных участков графиков прослеживания забойного давления влияет изменение проницаемости в призабойной зоне пласта. В зарубежной литературе это влияние именуется «скин-эффектом» (skin – пленка, оболочка).
рафик, построенный по результатам реальных промысловых исследований скважин, принимает форму прямой не сразу. На форму начальных участков графиков прослеживания забойного давления влияет изменение проницаемости в призабойной зоне пласта. В зарубежной литературе это влияние именуется «скин-эффектом» (skin – пленка, оболочка).
Рис. 50
В случае ограниченного пласта, когда изменение давления, вызванное закрытием скважины, доходит до его границы, КВД в скважине начнет искажаться, а через достаточно большое время выходит на горизонтальную асимптоту, соответствующую стационарному распределению давления. Поэтому длина прямолинейного участка на кривой ограничена (рис.50). Кроме того в реальных условиях скважину нельзя остановить мгновенно. После ее закрытия на устье приток флюида из пласта продолжается еще некоторое время из-за упругости жидкости и газов, заполняющих скважину. Время выхода на асимптоту, должно очевидно превышать время дополнительного притока. Поэтому возможны условия, при которых прямолинейный участок на КВД проявляется через значительный промежуток времени, либо даже вообще не существует.
Поскольку длительная остановка скважины нежелательна, были развиты методы определения параметров пласта на неустановившихся режимах, лишенных указанных недостатков и учитывающие, в частности, время работы скважины до ее остановки (метод Хорнера), а также приток флюида в скважину после ее остановки.
7. Приближенные методы решения задач теории упругого режима
Решение различных краевых задач неустановившейся фильтрации упругой жидкости в упругой пористой среде в условиях как бесконечного, так и конечного пластов часто представляются громоздкими формулами в виде бесконечного медленно сходящегося ряда или несобственного интеграла, содержащего специальные функции. В связи с этим были предприняты поиски приближенных эффективных решений задач неустановившейся фильтрации. Отметим лишь характерные особенности некоторых из разработанных приближенных методов, применяемых при решении задач упругого режима.
Одним из наиболее простых по идее приближенных методов решения задач неустановившейся фильтрации является метод последовательной смены стационарных состояний (ПССС), развитый И.А. Чарным и широко применяемый в практических расчетах. Метод основан на предположении, что давление в пласте изменяется во времени значительно медленнее, чем по координатам. Поэтому в основном уравнении упругого режима фильтрации (7.10) производную по времени можно в первом приближении отбросить, в результате чего для давления получается уравнение Лапласа, описывающее стационарный процесс. В этом случае в каждый момент времени вся область движения жидкости, в действительности охватывающая весь пласт, условно разделяется на две области: возмущенную и невозмущенную. При этом предполагается, что в возмущенной области, начинающейся от стенки скважины, давление распространяется так, как будто бы движение жидкости в ней установившееся; внешняя граница этой области служит контуром питания.
В невозмущенной области пласта давление всюду постоянно и равно начальному статическому. Закон движения подвижной границы раздела возмущенной и невозмущенной областей определяется при помощи уравнения материального баланса и граничных условий.
Рассмотрим схематично применение метода ПССС для случаев плоскопараллельного и плоскорадиального потоков упругой жидкости.
Прямолинейно-параллельный фильтрационный поток.
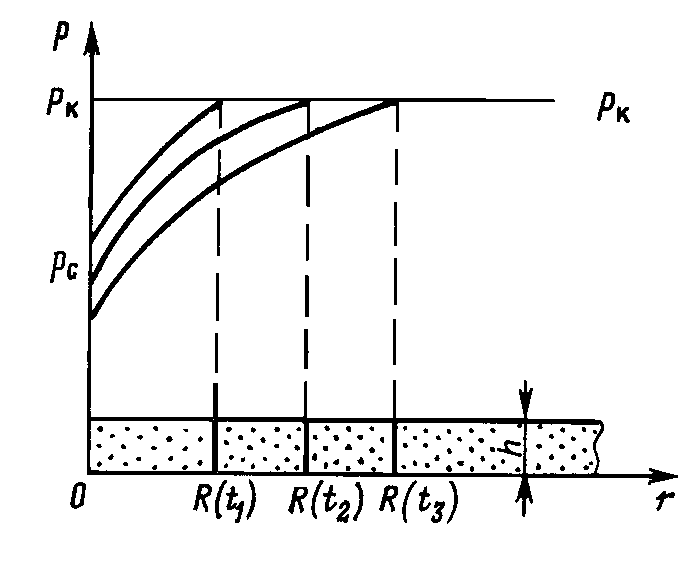
Рассмотрим полубесконечный горизонтальный пласт во всей области которого первоначально существовало постоянное давление Рк. В начальный момент времени (t=0) в сечении Х=0 пласта толщиной h и шириной В давление внезапно снизилось и стало равным Рг= const. К некоторому моменту времени t0 после пуска галереи граница возмущенной области распространилась на длину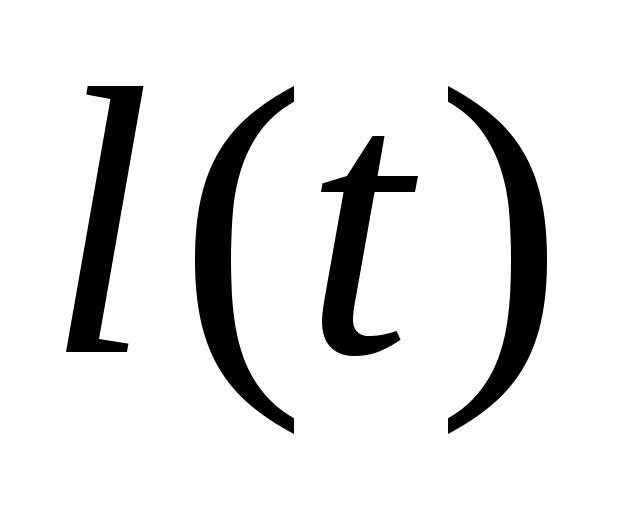 . (Рис.51) .
. (Рис.51) .
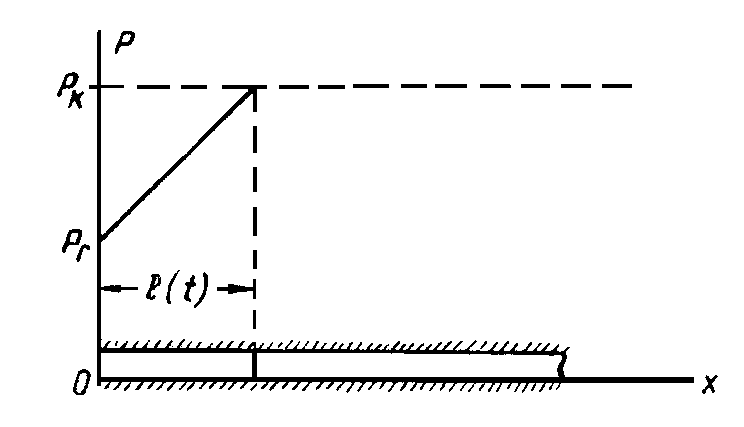
Рис.51
Распределение давления в возмущенной зоне принимается установившимся
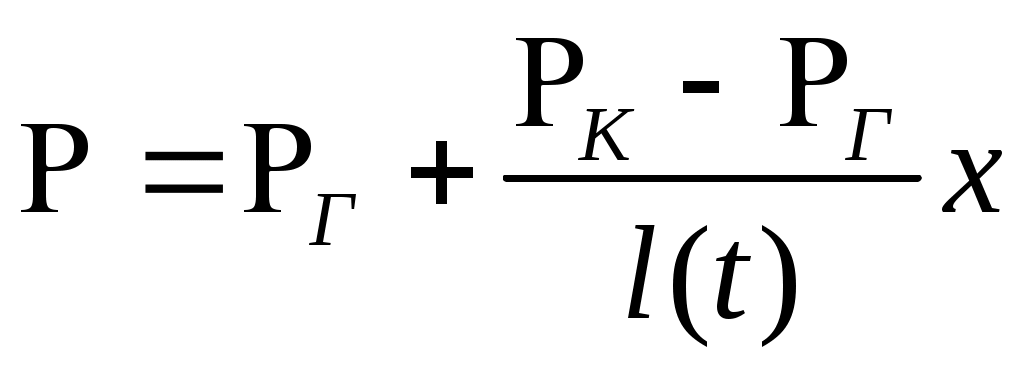 , (7.52)
, (7.52)
т.е. эпюра давлений Р(x) представляет собой прямую линию, перемещающуюся вдоль пласта с угловой точкой x=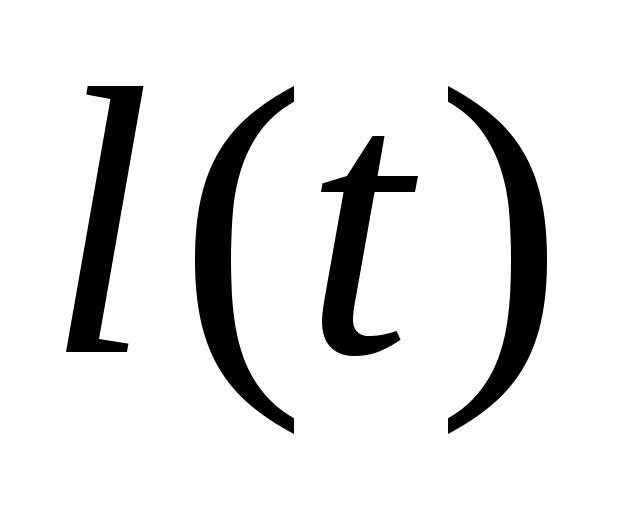 . Заметим, что в точном решении этой задачи эпюра давлений угловой точки не имеет.
. Заметим, что в точном решении этой задачи эпюра давлений угловой точки не имеет.
Рассматривая массу жидкости, отобранной за счет ее упругости из возмущенной области пласта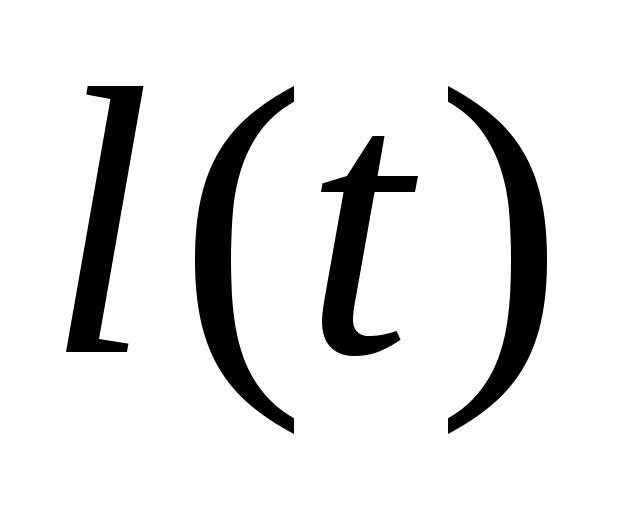 , ее массовый расход, выраженный по закону Дарси, получаем дифференциальное уравнение для границы
, ее массовый расход, выраженный по закону Дарси, получаем дифференциальное уравнение для границы 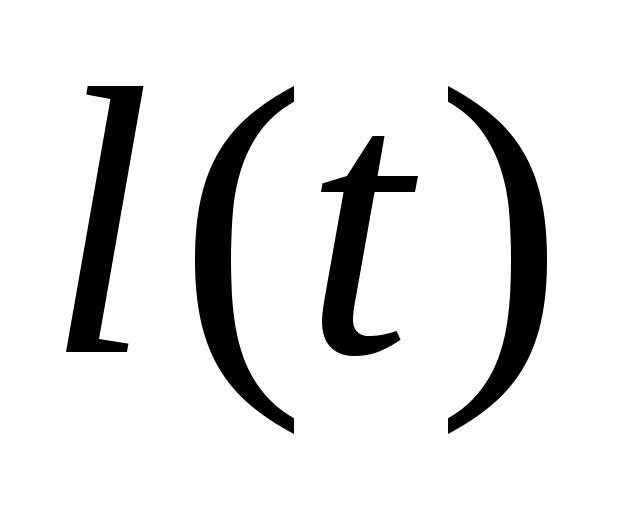 возмущенной зоны пласта, интегрирование которого дает закон движения этой границы:
возмущенной зоны пласта, интегрирование которого дает закон движения этой границы:
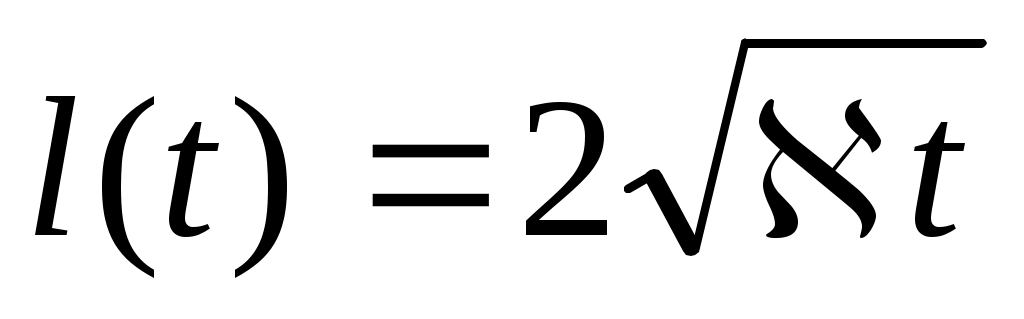 . (7.53)
. (7.53)
Тогда закон распределения давления в возмущенной зоне пласта (7.52) принимает вид
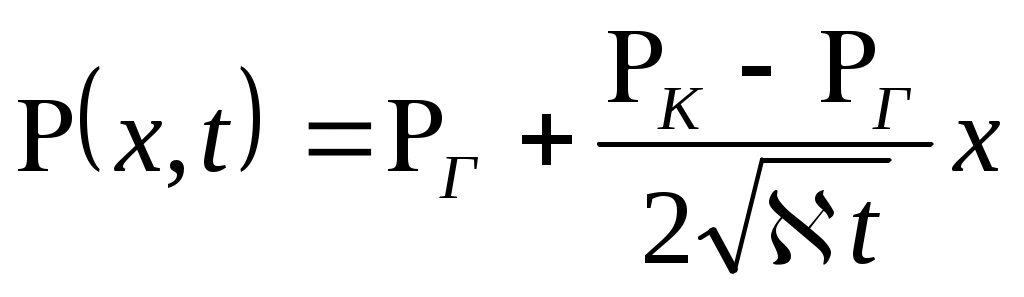 ,
,
или
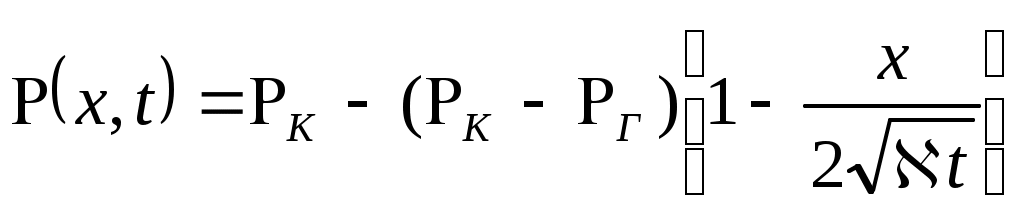 ; (7.54)
; (7.54)
где 0 < x 2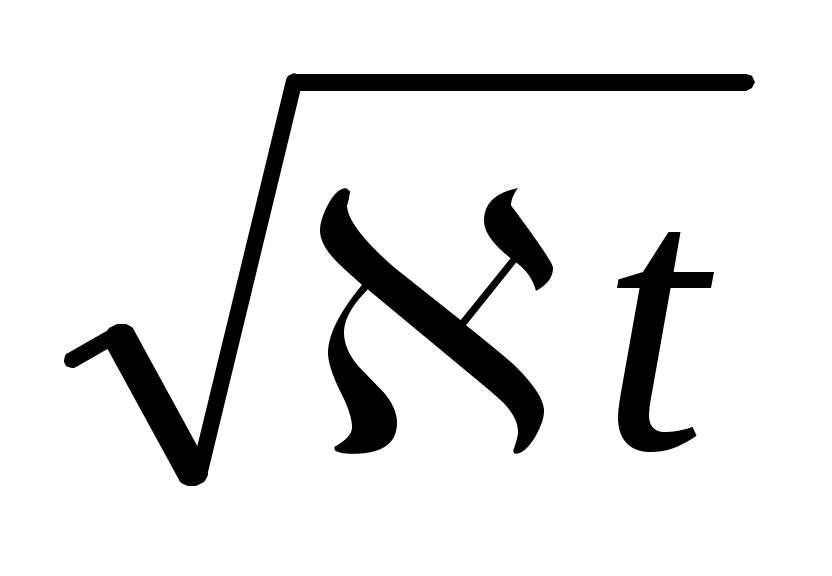 ;
;
а при x >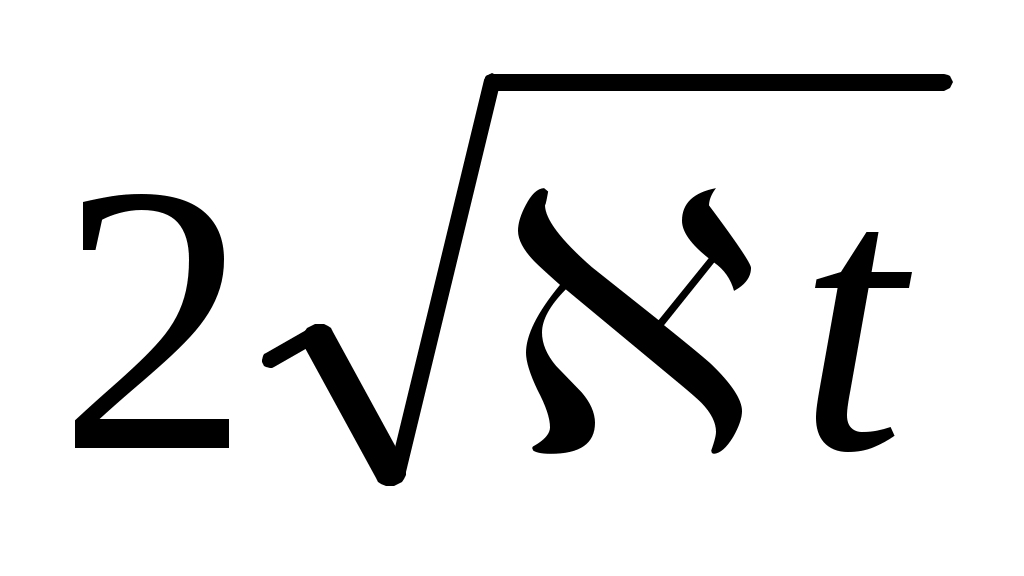 ,
, 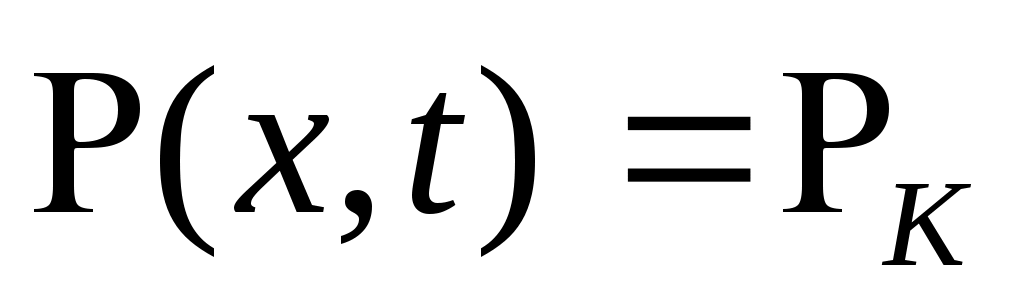 .
.
Нетрудно определить дебит галереи:
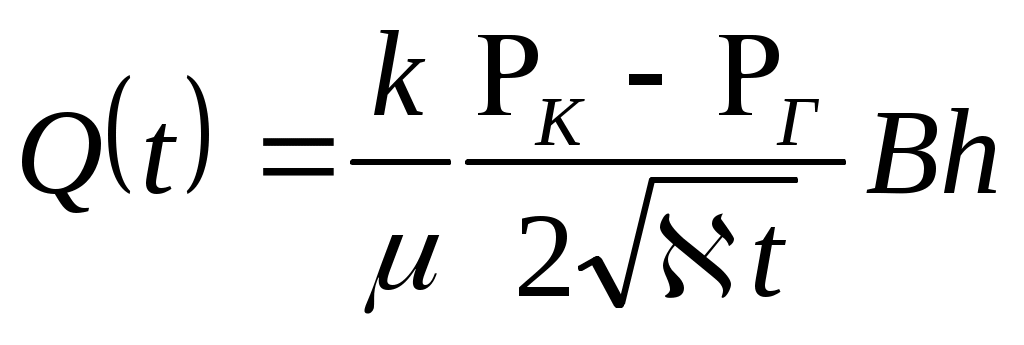 . (7.55)
. (7.55)
Погрешность расчета дебита галереи по приближенной формуле (7.55) по сравнению с расчетами по точной формуле (7.24) не превосходит 11%.
Плоскорадиальный фильтрационный поток.
Рассмотрим плоскорадиальный приток упругой жидкости к скважине радиуса rc из неограниченного горизонтального пласта постоянной толщины h (рис.52); скважина работает с постоянным дебитом Q; первоначально давление во всем пласте было одинаковым и равным Рк.
где
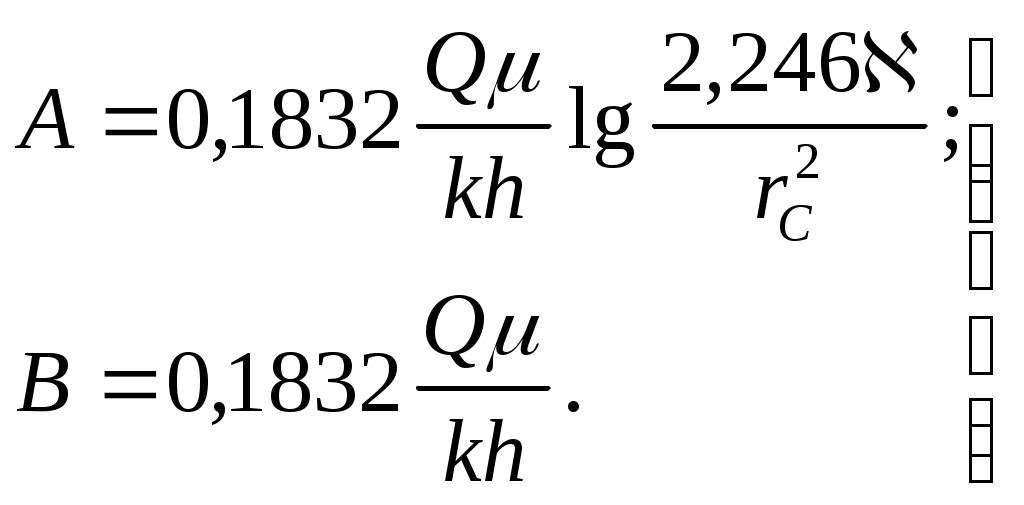 (7.45)
(7.45)Как видно из формул (7.43) и (7.44) изменение (снижение) забойного давления в пущенной с постоянным дебитом Q скважине оказывается линейной функцией логарифма времени. Следовательно, эти формулы можно рассматривать как уравнение графика изменения забойного давления после пуска скважины в эксплуатацию.
Рассмотрим теперь кривую восстановления забойного давления, т.е. рост забойного давления после мгновенной остановки скважины. Будем считать, что до остановки скважина длительное время работала с постоянным дебитом Q и вокруг нее в пласте имело место установившееся распределение пластового давления в соответствии с формулой (3.25)
 ,
,т.е. пьезометрическая линия является кривой логарифмического типа.
Изменение забойного давления после мгновенной остановки скважины можно определить, используя принцип суперпозиции:
где С. уст – депрессия на пласт при установившейся работе добывающей скважины с дебитом Q:
С. неуст – изменение давления на забое воображаемой нагнетательной скважины, пущенной в момент t=0 с расходом Q:
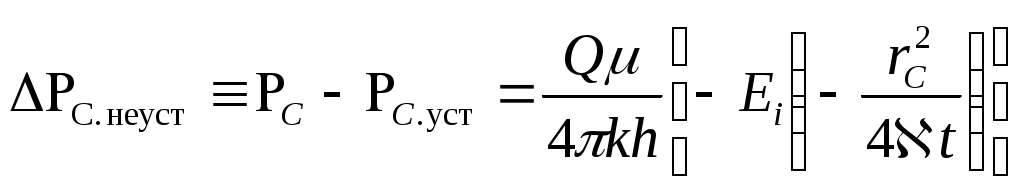 . (7.48)
. (7.48)Так как уст величина постоянная (от времени не зависит), то изменение забойного давления С будет определяться по формуле (7.48), которая совпадает с формулами (7.43) и (7.44).
Обработка кривых восстановления забойного давления и определения по ним коллекторских свойств пласта проводятся следующим образом. Снятую скважинным манометром кривую восстановления забойного давления после остановки скважины перестраивают в координатах (С, lg t). По прямому участку этой кривой (рис.50) находится отрезок, отсекаемый ее продолжением на оси С
(отрезок А), и тангенс угла наклона этой прямой к оси абсцисс (B=tg ). Затем с помощью второго равенства (7.45) определяется параметр
Если известны вязкость жидкости в пластовых условиях и толщина пласта h, то из последней формулы находится коэффициент проницаемости пласта
Далее по известному угловому коэффициенту B=tg и радиусу скважины из первого равенства (7.45)
можно определить коэффициент пьезопроводности пласта
Отметим, что область применения указанных простых приемов интерпретации результатов исследования нефтяных скважин ограничивается условиями, при которых справедлива формула (7.37), а именно:
скважина рассматривается как источник постоянной интенсивности в бесконечном однородном пласте, и возможна мгновенная остановка притока флюида в скважину.
Г
 рафик, построенный по результатам реальных промысловых исследований скважин, принимает форму прямой не сразу. На форму начальных участков графиков прослеживания забойного давления влияет изменение проницаемости в призабойной зоне пласта. В зарубежной литературе это влияние именуется «скин-эффектом» (skin – пленка, оболочка).
рафик, построенный по результатам реальных промысловых исследований скважин, принимает форму прямой не сразу. На форму начальных участков графиков прослеживания забойного давления влияет изменение проницаемости в призабойной зоне пласта. В зарубежной литературе это влияние именуется «скин-эффектом» (skin – пленка, оболочка).Рис. 50
В случае ограниченного пласта, когда изменение давления, вызванное закрытием скважины, доходит до его границы, КВД в скважине начнет искажаться, а через достаточно большое время выходит на горизонтальную асимптоту, соответствующую стационарному распределению давления. Поэтому длина прямолинейного участка на кривой ограничена (рис.50). Кроме того в реальных условиях скважину нельзя остановить мгновенно. После ее закрытия на устье приток флюида из пласта продолжается еще некоторое время из-за упругости жидкости и газов, заполняющих скважину. Время выхода на асимптоту, должно очевидно превышать время дополнительного притока. Поэтому возможны условия, при которых прямолинейный участок на КВД проявляется через значительный промежуток времени, либо даже вообще не существует.
Поскольку длительная остановка скважины нежелательна, были развиты методы определения параметров пласта на неустановившихся режимах, лишенных указанных недостатков и учитывающие, в частности, время работы скважины до ее остановки (метод Хорнера), а также приток флюида в скважину после ее остановки.
7. Приближенные методы решения задач теории упругого режима
Решение различных краевых задач неустановившейся фильтрации упругой жидкости в упругой пористой среде в условиях как бесконечного, так и конечного пластов часто представляются громоздкими формулами в виде бесконечного медленно сходящегося ряда или несобственного интеграла, содержащего специальные функции. В связи с этим были предприняты поиски приближенных эффективных решений задач неустановившейся фильтрации. Отметим лишь характерные особенности некоторых из разработанных приближенных методов, применяемых при решении задач упругого режима.
-
Метод последовательной смены стационарных состояний (ПССС)
Одним из наиболее простых по идее приближенных методов решения задач неустановившейся фильтрации является метод последовательной смены стационарных состояний (ПССС), развитый И.А. Чарным и широко применяемый в практических расчетах. Метод основан на предположении, что давление в пласте изменяется во времени значительно медленнее, чем по координатам. Поэтому в основном уравнении упругого режима фильтрации (7.10) производную по времени можно в первом приближении отбросить, в результате чего для давления получается уравнение Лапласа, описывающее стационарный процесс. В этом случае в каждый момент времени вся область движения жидкости, в действительности охватывающая весь пласт, условно разделяется на две области: возмущенную и невозмущенную. При этом предполагается, что в возмущенной области, начинающейся от стенки скважины, давление распространяется так, как будто бы движение жидкости в ней установившееся; внешняя граница этой области служит контуром питания.
В невозмущенной области пласта давление всюду постоянно и равно начальному статическому. Закон движения подвижной границы раздела возмущенной и невозмущенной областей определяется при помощи уравнения материального баланса и граничных условий.
Рассмотрим схематично применение метода ПССС для случаев плоскопараллельного и плоскорадиального потоков упругой жидкости.
Прямолинейно-параллельный фильтрационный поток.
Рассмотрим полубесконечный горизонтальный пласт во всей области которого первоначально существовало постоянное давление Рк. В начальный момент времени (t=0) в сечении Х=0 пласта толщиной h и шириной В давление внезапно снизилось и стало равным Рг= const. К некоторому моменту времени t0 после пуска галереи граница возмущенной области распространилась на длину

Рис.51
Распределение давления в возмущенной зоне принимается установившимся
т.е. эпюра давлений Р(x) представляет собой прямую линию, перемещающуюся вдоль пласта с угловой точкой x=
Рассматривая массу жидкости, отобранной за счет ее упругости из возмущенной области пласта
Тогда закон распределения давления в возмущенной зоне пласта (7.52) принимает вид
или
где 0 < x 2
а при x >
Нетрудно определить дебит галереи:
Погрешность расчета дебита галереи по приближенной формуле (7.55) по сравнению с расчетами по точной формуле (7.24) не превосходит 11%.
Плоскорадиальный фильтрационный поток.
Рассмотрим плоскорадиальный приток упругой жидкости к скважине радиуса rc из неограниченного горизонтального пласта постоянной толщины h (рис.52); скважина работает с постоянным дебитом Q; первоначально давление во всем пласте было одинаковым и равным Рк.



