Рис. 52
После пуска скважины в работу вокруг нее образуется воронка депрессии, которая теоретически охватывает весь пласт. Приближение в решении задачи заключается в том, что мы последовательно во времени фиксируем радиус воронки депрессии, т.е. в каждый момент времени радиус воронки R(t) принимается как конечная величина. При этом кривая распределения давления аппроксимируется логарифмической кривой, т.е.
. (7.56)
При этом дебит скважины будет описываться формулой, аналогичной формуле Дюпюи:
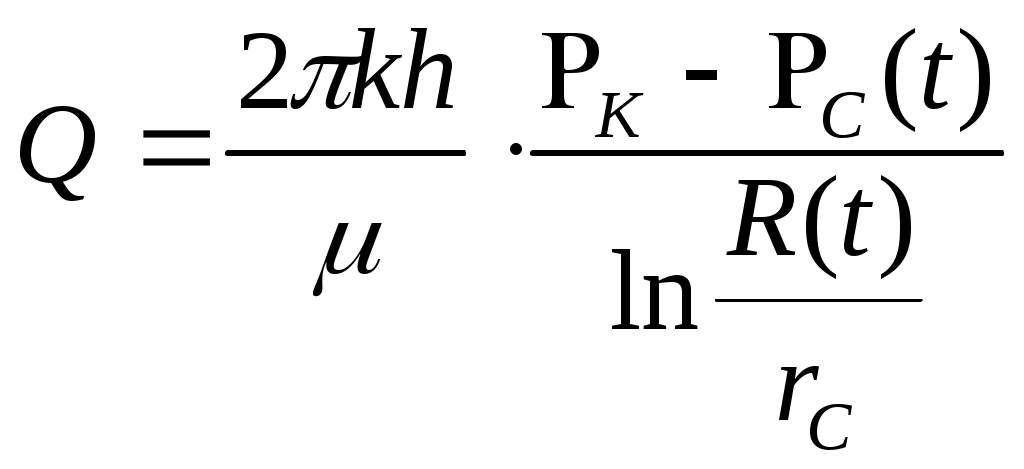. (7.57)
Размер возмущенной области R(t) также находится из рассмотрения уравнения материального баланса для упругой жидкости, отобранной из этой области пласта. В итоге закон движения границы R(t) возмущенной зоны пласта имеет вид:
. (7.58)
Тогда из равенства (7.56) находится давление в любой точке пласта в любой момент времени t:
, (7.59)
где ,

а при

Депрессия на скважине (r = r_C) в момент t будет:
(7.60)
Сравнивая (7.60) с депрессией, определенной по точной формуле (7.39), убеждаемся, что относительная погрешность уменьшается с течением времени и составляет:

10,6 % , если ;

7,5 %, если ;

5,7 %, если .

2. 
   Метод А.М. Пирвердяна
   

Этот метод аналогичен методу ПССС и уточняет его. В методе А.М. Пирвердяна, как и в методе ПССС неустановившийся фильтрационный поток в каждый момент времени мысленно разбивается на две области – возмущенную и невозмущенную. Граница между этими областями также определяется из уравнения материального баланса. Но в отличие от метода ПССС распределение давления в возмущенной области по методу А.М.Пирвердяна задается в виде квадратичной параболы так, чтобы пьезометрическая кривая по границе областей касалась горизонтальной линии, представляющей давление в невозмущенной области.

---

Распределение давления уже не будет стационарным, а градиент давления по границе областей становится равным нулю, что обеспечивает плавное смыкание профиля давлений в возмущенной и невозмущенной областях.

Р
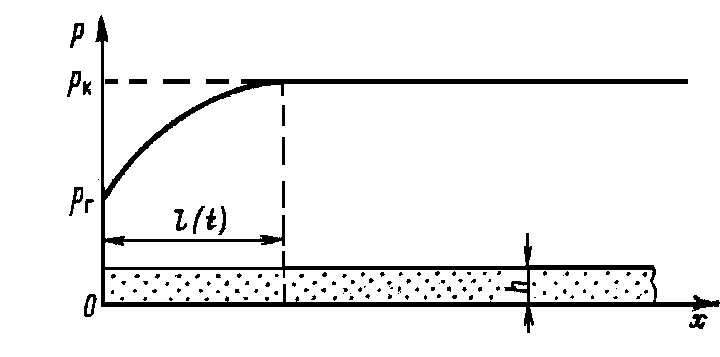
ис. 53

Рассмотрим прямолинейно-параллельный фильтрационный поток упругой жидкости (рис.53). В горизонтальном пласте постоянной толщины h и ширины B пущена в эксплуатацию галерея с постоянным дебитом Q . К моменту времени t после пуска граница возмущенной области продвигается на величину , при этом кривая распределения давления в этой области задается в виде параболы так, что в точке касательная к параболе горизонтальна, т.е.

(7.61)

Дебит галереи определяется по закону Дарси
. (7.62)

Учитывая (7.61), находим выражение для дебита галереи
. (7.63)
Закон движения внешней границы возмущенной области определяется из уравнения материального баланса (как и при методе ПССС) и имеет вид:

. (7.64)
Распределение давления (7.61) в возмущенной области пласта с учетом (7.63) и (7.64) принимает вид
, (7.65)
где ;

при .

Расчет депрессии по формуле (7.65) дает погрешность по сравнению с точным решением примерно 9%, т.е. в 2,5 раза меньше, чем метод ПССС.

---

Аналогичным образом строится решение и для случая плоскорадиального потока. В этом случае распределение давления в возмущенной области пласта задается в виде
, (7.66)
где R(t) - радиус внешней границы возмущенной области пласта.

Заметим, что отбросив последнее слагаемое в уравнении (7.66), получаем закон распределения давления при методе ПССС.

3. 
   Метод интегральных соотношений
   

Метод интегральных соотношений, предложенный Г.И. Баренблаттом, по аналогии с методом пограничного слоя в потоке вязкой жидкости, позволяет получить приближенные решения некоторых задач нестационарной фильтрации упругой жидкости с нужной точностью.

Основные особенности метода Г.И. Баренблатта рассмотрим на примере неустановившегося плоскорадиального притока жидкости к скважине после ее пуска в эксплуатацию. В этом случае распределение пластового давления в возмущенной области вокруг скважины представляется в виде многочлена по степеням координаты r с коэффициентами, зависящими от времени, т.е.
(7.67)

.

Задача сводится к нахождению коэффициентов А, B₀, B₁, B₂,...., B_n, которые должны удовлетворять граничным условиям, т.е. условиям на стенке скважины и на внешней границе возмущенной области. Кроме того эти коэффициенты должны удовлетворять выведенным Г.И. Баренблаттом особым интегральным соотношениям. Число этих интегральных соотношений зависит от показателя степени n, а следовательно, от числа членов многочлена, входящего в уравнение (7.67). Показатель степени n в свою очередь выбирается в зависимости от желательной степени точности решения задачи. Чем больше число n, тем выше точность решаемой задачи. Г.И.Баренблат показал, что если принять n=0 (в этом случае интегральное соотношение сводится к уравнению материального баланса), то из его метода, как частный случай, получается метод последовательной смены стационарных состояний (ПССС).

Если принять n=1, то из метода Баренблатта вытекает, как частный случай, метод А.М.Пирвердяна; в этом легко убедиться, положив в уравнение (7.67) n=1 и сравнив его с уравнением (7.66).

---

Смотрите также файлы

• Управление цепями поставок (часть 11) Кокурин Д. И.pdf

• Д. В. Меланьин Самоучитель практического гипноза.doc

• Практических заданий по дисциплине экономикоматематические методы и модели в логистике.docx

• Отчет о проделанной работе молодого специалиста с наставником за 1 полугодие в 20222023 учебном году.docx

• Исследование распределения токов, напряжений и мощностей при различных способах соединения пассивных элементов.docx