Файл: Задание 20. Задачи на логику и смекалку Тип 27 (про множители).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.04.2024
Просмотров: 35
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание № 20. Задачи на логику и смекалку
Тип № 27 (про множители)
Если бы каждый из двух множителей увеличили на 1, их произведение увеличилось бы на 11. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 2?
Решение.
Пусть a, b — соответственно первое и второе число. При увеличении каждого из множителей на 1 их произведение увеличивается на 11:
Найдём на сколько увеличится произведение этих множителей при увеличении каждого из них на 2:
Таким образом, при увеличении каждого из множителей на 2, их произведение увеличивается на 24.
Ответ: 24.
Задания для самостоятельного решения
1. Если бы каждый из двух множителей увеличили на 1, их произведение увеличилось бы на 8. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 3?
2. Если бы каждый из двух множителей увеличили на 2, их произведение увеличилось бы на 12. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 3?
Тип № 28 (про доски)
Взяли несколько досок и распилили их. Всего сделали 11 поперечных распилов, в итоге получилось 16 кусков. Сколько досок взяли?
Решение.
Каждый поперечный распил добавляет один кусок к уже имеющимся, следовательно, изначально было 16 − 11 = 5 досок.
Ответ: 5.
Задания для самостоятельного решения
1. Взяли несколько досок и распилили их. Всего сделали 5 поперечных распилов, в итоге получилось 23 куска. Сколько досок взяли?
2. Взяли несколько досок и распилили их. Всего сделали 24 поперечных распила, в итоге получилось 33 куска. Сколько досок взяли?
Тип № 25 (про отметки)
В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 690. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённая по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; а 2,8 — до 3.)
Решение.
Разложим число 690 на множители так, чтобы получившиеся множители состояли только из чисел 2, 3, 4, 5, и общее количество цифр в произведении было равно пяти: 690 = 2 · 5 · 23 · 3. Следовательно, учитель поставил Пете отметки 2, 5, 2, 3 и 3. Среднее арифметическое этих оценок:
Ответ: 3.
Задания для самостоятельного решения
1. В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 3495. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённая по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; а 2,8 — до 3.)
2. В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 3530. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённая по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; а 2,8 — до 3.)
Тип № 26 (про фишки)
Петя меняет маленькие фишки на большие. За один обмен он получает 3 большие фишки, отдав 10 маленьких. До обменов у Пети было 100 фишек (среди них были и большие, и маленькие), а после стало 65. Сколько обменов он совершил?
Решение.
За один обмен количество фишек у Пети уменьшается на 10 − 3 = 7 штук. Следовательно, Петя совершил (100 − 65)/7 = 5 обменов.
Ответ: 5.
Задания для самостоятельного решения
1. Петя меняет маленькие фишки на большие. За один обмен он получает 6 больших фишек, отдав 9 маленьких. До обменов у Пети было 100 фишек (среди них были и большие, и маленькие), а после стало 79. Сколько обменов он совершил?
2. Петя меняет маленькие фишки на большие. За один обмен он получает
4 большие фишки, отдав 10 маленьких. До обменов у Пети было 100 фишек (среди них были и большие, и маленькие), а после стало 64. Сколько обменов он совершил?
Тип № 23 (про столбы)
Десять столбов соединены между собой проводами так, что от каждого столба отходит ровно 8 проводов. Сколько всего проводов протянуто между этими десятью столбами?
Решение.
От каждого столба отходит по 8 проводов, следовательно, всего будет
соединений. Заметим, что каждые два столба связаны одни проводом, поэтому между этими десятью столбами будет протянуто всего 
проводов.Ответ: 40.
Задания для самостоятельного решения
1. Десять столбов соединены между собой проводами так, что от каждого столба отходит ровно 4 провода. Сколько всего проводов протянуто между этими десятью столбами?
2. Восемь столбов соединены между собой проводами так, что от каждого столба отходит ровно 6 проводов. Сколько всего проводов протянуто между этими восемью столбами?
3. Двенадцать столбов соединены между собой проводами так, что от каждого столба отходит ровно четыре провода. Сколько всего проводов протянуто между этими двенадцатью столбами?
Тип № 24 (про договоры)
Из десяти стран четыре подписали договор о дружбе ровно с пятью другими странами, а каждая из оставшихся шести — ровно с тремя. Сколько всего было подписано договоров?
Решение.
Четыре страны поставили 4 · 5 = 20 подписей. А оставшиеся шесть стран поставили 6 · 3 = 18 подписей. Ясно, что договоров в два раза меньше, чем общее количество подписей, то есть всего было подписано (20 + 18)/2 = 19 договоров.
Ответ: 19.
Задания для самостоятельного решения
1. Из десяти стран семь подписали договор о дружбе ровно с тремя другими странами, а каждая из оставшихся трёх – ровно с семью. Сколько всего было подписано договоров?
2. Из десяти стран семь подписали договор о дружбе ровно с тремя другими странами, а каждая из оставшихся трёх — ровно с семью. Сколько всего было подписано договоров?
3. Из десяти стран семь подписали договор о дружбе ровно с пятью другими странами, а каждая из оставшихся трёх — ровно с семью. Сколько всего было подписано договоров?
Тип № 21 (про вазы)
На прилавке цветочного магазина стоят 3 вазы с розами: белая, синяя и красная. Слева от красной вазы 15 роз, справа от синей вазы 12 роз. Всего в вазах 22 розы. Сколько роз в белой вазе?
Решение.
Выясним относительное расположение ваз с розами. Будем обозначать положение вазы соответствующей буквой. Если вазы расположены в порядке Б−С−К, то получится, что в белой и синей вазах в сумме 15 роз, в красной 12 роз, то есть в сумме 27 роз, что противоречит условию задачи. Если вазы располагаются в порядке Б−К−С получаем аналогичное противоречие. Порядок К−Б−С невозможен, потому что тогда справа от синей вазы и слева от красной вазы нет роз. Непротиворечивое расположение ваз: С−Б−К. Будем также обозначать количество роз в вазе соответствующей буквой. Тогда получим систему уравнений:
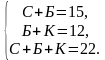
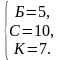
Таким образом, в белой вазе 5 роз.
Ответ: 5.
Задания для самостоятельного решения
1. На прилавке цветочного магазина стоят 3 вазы с розами: оранжевая, белая и синяя. Слева от синей вазы 15 роз, справа от белой вазы 11 роз. Всего в вазах 23 розы. Сколько роз в оранжевой вазе?
2. На прилавке цветочного магазина стоят 3 вазы с розами: белая, жёлтая и оранжевая. Слева от жёлтой вазы 22 розы, справа от оранжевой вазы 23 розы. Всего в вазах 35 роз. Сколько роз в белой вазе?
Тип № 22 (про лучи)
Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 2 раза больше наименьшего. Сколько значений может принимать величина среднего угла?
Решение.
Пусть α − величина наименьшего угла, β − величина среднего угла, тогда 2α − величина наибольшего угла. Полный угол равен 360°, следовательно, α + β + 2α = 360, откуда β = 360 − 3α. Средний угол должен быть больше меньшего угла и меньше большего, то есть:
Угол β принимает только значения, измеряемые целым числом градусов, поэтому угол β может принимать 90 − 72 − 1 = 17 значений.
Ответ: 17.
Примечание.
Вычитанием единицы в последнем действии учитывается, что значения 72° и 90° не входят в число значений подсчитываемых углов.
Задания для самостоятельного решения
1. Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 6 раз больше наименьшего. Сколько значений может принимать величина среднего угла?
2. Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 3 раза больше наименьшего. Сколько значений может принимать величина среднего угла?
Тип № 19 (про теннис)
Миша, Коля и Лёша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 9 партий, а Коля — 19. Сколько партий сыграл Лёша?
Решение.
Больше всех партий сыграл Коля, следовательно, было сыграно не менее 19 партий. В одной из первых двух партий должен был участвовать Миша, значит, было сыграно не более
партии. Значит, Коля участвовал в каждой сыгранной партии. Таким образом, Лёша сыграл 19 − 9 = 10 партий.Ответ: 10.
Задания для самостоятельного решения
1. Миша, Коля и Лёша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 13 партий, а Коля — 27. Сколько партий сыграл Лёша?
2. Миша, Коля и Лёша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 12 партий, а Коля — 25. Сколько партий сыграл Лёша?
Тип № 20 (про викторину)
Список заданий викторины состоял из 36 вопросов. За каждый правильный ответ ученик получал 5 очков, за неправильный ответ с него списывали 11 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 75 очков, если известно, что по крайней мере один раз он ошибся?
Решение.
Пусть х – количество верных ответов
у – количество неверных ответов.
Тогда составим уравнение 5х - 11у = 75, где 0 и 0. Из уравнения видно, что у делится на 5.
Пусть: 1)у=5, тогда5х = 75 + 11у= 75 + 55=130,х = 130 : 5 = 26и это меньше 36.
2)у=10,тогда5х =75 +11у=75+110=185, х = 185 : 5=37,но это больше 36.
Ответ: 26.
Задания для самостоятельного решения
1. Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получил 7 очков, за неправильный ответ с него списывали 11 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 84 очка, если известно, что по крайней мере один раз он ошибся?
2. Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 5 очков, за неправильный ответ с него списывали 8 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 50 очков, если известно, что по крайней мере один раз он ошибся?
