3. Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 12 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 70 очков, если известно, что по крайней мере один раз он ошибся?

4. Список заданий викторины состоял из 40 вопросов. За каждый правильный ответ ученик получал 9 очков, за неправильный ответ с него списывали 11 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 171 очко, если известно, что по крайней мере один раз он ошибся?

Тип № 17 (про страницы)

Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 372, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?

Решение.

Из числа 372 можно составить числа 327, 273, 237, 723, 732. Числа 327, 273 и 237 не подходят, поскольку они меньше числа 372. Номер первой страницы после выпавших листов должен быть нечётным, поскольку номер последней страницы перед выпавшими листами чётный. Следовательно, нам подходит только число 723. Вычтем из числа 723 одну страницу, поскольку страница 723 не выпала, а является первой страницей после выпавших листов. Теперь можно найти количество выпавших листов: 



 

Ответ: 175.

Задания для самостоятельного решения

1. Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 276, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?

2. Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 274, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?

3. Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 294, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?

Тип № 18 (про натуральные числа)

Про натуральные числа A, B и С известно, что каждое из них больше 4, но меньше 8. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 165. Какое число было загадано?

---

Решение.

Числа  А, В и С могут быть равны 5, 6 или 7.

Пусть загадали натуральное число Х, тогда Х · А + В – С = 165 или Х · А = 165 + (C – B). Рассмотрим различные случаи.

1) С – В = 0 (7 – 7 = 0, 6 – 6 = 0 или 5 – 5 = 0), тогда Х · А = 165. Число 165 делится нацело на A = 5, значит, Х = 33.

2) С – В = 1 (7 – 6 = 1 или 6 – 5 = 1), тогда Х · А = 166. Число 166 не делится нацело на 5, на 6 и на 7, значит, этот случай не подходит.

3) С – В = –1 (6 – 7 = –1 или 5 – 6 = –1), тогда Х · А = 164. Число 164 не делится нацело на 5, на 6 и на 7, значит, этот случай не подходит.

4) С – В = 2 (7 – 5 = 2), тогда Х · А = 167. Число 167 не делится нацело на 5, на 6 и на 7, значит, этот случай не подходит.

5) С – В = –2 (5 – 7 = –2), тогда Х·А = 163. Число 163 не делится нацело на A = 5, на 6 и на 7, значит, этот случай не подходит.

Ответ: 33.

Задания для самостоятельного решения

1. Про натуральные числа A, B и С известно, что каждое из них больше 4, но меньше 8. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 417. Какое число было загадано?

2. Про натуральные числа A, B и С известно, что каждое из них больше 4, но меньше 8. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 213. Какое число было загадано?

3. Про натуральные числа A, B и С известно, что каждое из них больше 6, но меньше 10. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 186. Какое число было загадано?

Тип № 15 (про Машу и Медведя)

Маша и Медведь съели 100 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенья, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?

Решение.

1. Так как варенье и Маша, и Медведь съели поровну, и при этом Медведь ел варенье в 3 раза быстрее, то Маша ела варенье (свою половину) в 3 раза дольше, чем Медведь (такую же половину).

2. Тогда получается, что Медведь ел печенья в 3 раза дольше Маши и к тому же ел их в 3 раза быстрее, то есть, на одно съеденное Машей печенье приходилось 3∙3=9 печений, съеденных Медведем.

---

3. В сумме эти печенья составляют 1+9=10 и таких сумм в 100 печеньях ровно
100:10 = 10.

4. Значит, Маша съела 10 печений, а Медведь 9∙10=90.

Ответ: 90.

Задания для самостоятельного решения

1. Маша и Медведь съели 51 печенье и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенья, но в какой-то момент они поменялись. Медведь и то, и другое ест в четыре раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?

2. Маша и Медведь съели 160 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь - печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенье они съели поровну?

3. Маша и Медведь съели 120 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенье, но в какой-то момент они поменялись. Медведь и то и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?

Тип № 16 (про квас)

В магазине квас на разлив можно купить в бутылках, причём стоимость кваса в бутылке складывается из стоимости самой бутылки и кваса, налитого в неё. Цена бутылки не зависит от её объёма. Бутылка кваса объёмом 1 литр стоит 40 рублей, объёмом 2 литра — 70 рублей. Сколько рублей будет стоить бутылка кваса объёмом 0,5 литра?

Решение.

Пусть стоимость бутылки x руб., стоимость кваса за литр y руб. Имеем систему уравнений:

 

 

 

Значит, бутылка стоит 10 руб., а 1 литр кваса – 30 руб. Тогда бутылка кваса объёмом 0,5 литра будет стоить 10 + 30 · 0,5 = 25 рублей.

 

Тип № 13 (про числа)

1. В таблице три столбца и несколько строк. В каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна 119, во втором - 125, в третьем - 133, а сумма чисел в каждой строке больше 15, но меньше 18. Сколько всего строк в столбце?

Решение.

Общая сумма во всех столбцах = 119 + 125 + 133 = 377.

Числа 18 и 15 не включены в предел, значит:

1) если сумма в строке = 17, то, количество строк равно 377 : 17= 22,2;

2) если сумма в строке = 16, то, количество строк равно 377 : 16= 23,5.

Значит, количество строк = 23 (т.к. оно должно быть между 22,2 и 23,5).

Ответ: 23.

Задания для самостоятельного решения

---

1. В таблице 3 столбца и несколько строк. В каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна 98, во втором -103, в третьем - 99, а сумма чисел каждой строке больше 26, но меньше 29. Сколько всего строк в таблице?

2. В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 72, во втором — 81, в третьем — 91, а сумма чисел в каждой строке больше 13, но меньше 16. Сколько всего строк в таблице?


Тип № 14 (про среднее арифметическое)

1. Среднее арифметическое 6 различных натуральных чисел равно 8. На сколько нужно увеличить наибольшее из этих чисел, чтобы их среднее арифметическое стало на 1 больше?

Решение.

Среднее арифметическое находится как сумма чисел разделенное на их количество. В нашем случае среднее арифметическое равно 8, а количество чисел – 6. Получается, что   , где x – сумма 6 различных натуральных чисел. Отсюда, сумма шести натуральных чисел равна x = 6⋅8 = 48. При увеличении среднего арифметического на 1, т.е. до 9 неважно какое именно число необходимо увеличивать. Посчитаем при среднем арифметическом равном 9, сколько будет сумма 6 различных натуральных чисел 
  откуда x = 9 ⋅ 6 = 54. Значит, сумму 6 натуральных чисел (в нашем случае наибольшее) необходимо увеличить на 54 − 48 = 6, чтобы среднее арифметическое увеличилось на 1.

Ответ: 6.

2. Среднее арифметическое шести различных натуральных чисел равно 8. Среднее арифметическое этих чисел и седьмого числа равно 9. Чему равно седьмое число?

Решение.

Сумма первых шести чисел равна S₆ = 6 · 8 = 48. Запишем выражение для среднего арифметического семи чисел:    

Откуда   .

Ответ: 15.

Задания для самостоятельного решения

1. Среднее арифметическое 7 различных натуральных чисел равно 12. На сколько нужно увеличить наибольшее из этих чисел, чтобы их среднее арифметическое стало на 2 больше?

---

2. Среднее арифметическое 7 натуральных чисел равно 12. К ним добавили восьмое число такое, что среднее арифметическое этих восьми чисел равно 14. Найдите восьмое число.

3. Среднее арифметическое девяти чисел, записанных на доске, равно 14, а среднее арифметическое первых восьми из этих чисел равно 13. Найдите девятое число, записанное на доске.

Тип № 11 (про прямоугольник)

1. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.

Решение.



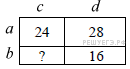
Введём обозначения, как показано на рисунке. Периметр верхнего левого прямоугольника равен 24, поэтому   аналогично, 

При помощи полученной системы уравнений выразим значение 



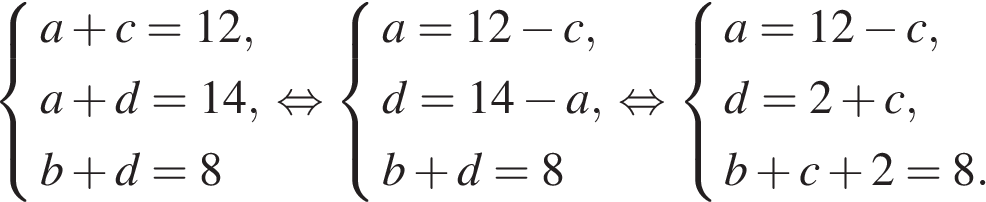
Из третьего уравнения получаем: 

Следовательно, искомый периметр равен 12.

Ответ: 12.

Примечание. Пусть   периметры прямоугольников, рассматриваемых по часовой стрелке с левого верхнего угла. Заметим, что искомый периметр



Действительно,   . Значит, 

2. Прямоугольник разбит на 4 маленьких прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с верхнего левого и далее по часовой стрелке, равны 9, 12, 32. Найдите площадь четвертого прямоугольника?

Решение.

---

Смотрите также файлы

• Сабаты таырыбы сімдіктерді суі мен дамуына жарыты сері. Жарыты тсу дегейіне арай сімдіктерді бейімделуі. Малімні атыжні.docx

• Вопросы с ответами Введение в специальность.docx

• Блім Видеожазба Педагогты атыжні.doc

• Период правления императора Российской империи Александра iii принято называть временем контрреформ.docx

• Занятие Дивидендная политика корпорации.docx