Файл: Контрольная работа дисциплина (модуль) Метрология, стандартизация и сертификация.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.04.2024
Просмотров: 52
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Откуда
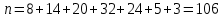
Получаем среднее арифметическое значение результатов измерений
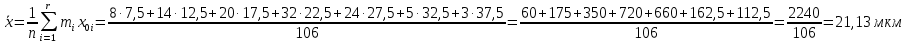
Среднее квадратичное отклонение (СКО)
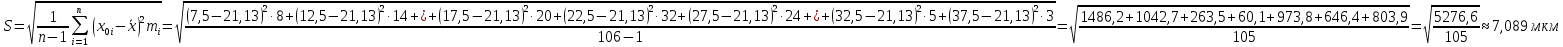
Производим повторную проверку по критерию Шарлье.
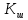 определяем по приложению А для
определяем по приложению А для  , так как для
, так как для 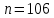
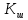 не определен
не определен
Определяем крайнее значение, которое имеет максимальную разность
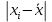

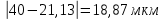
Проверяем крайнее значение 0 мкм.
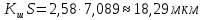
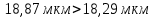
Значение 40 мкм является промахом. Исключаем значения интервала с границами 35; 40 мкм.
Пересчитываем среднее арифметическое значение и СКО в таблице 5.
Таблица 5 – Расчет среднего и СКО
| Номер интервала  | Границы интервала | 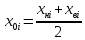 мкм | Абсолютная частота 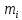 | 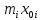 , мкм , мкм | 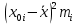 , мкм2 , мкм2 | ||||
| нижняя 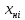 , мкм , мкм | верхняя 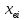 , мкм , мкм | ||||||||
| 1 | 5 | 10 | 7,5 | 8 | 60 | 1385,5 | |||
| 2 | 10 | 15 | 12,5 | 14 | 175 | 932,2 | |||
| 3 | 15 | 20 | 17,5 | 20 | 350 | 199,7 | |||
| 4 | 20 | 25 | 22,5 | 32 | 720 | 108,3 | |||
| 5 | 25 | 30 | 27,5 | 24 | 660 | 1122,9 | |||
| 6 | 30 | 35 | 32,5 | 5 | 162,5 | 700,9 | |||
| Сумма | - | - | - | 103 | 2127,5 | 4449,5 | |||
Откуда
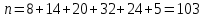
Получаем среднее арифметическое значение результатов измерений
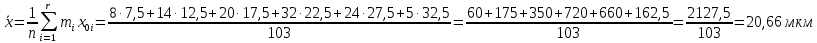
Среднее квадратичное отклонение (СКО)
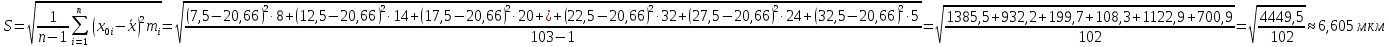
Производим повторную проверку по критерию Шарлье.
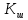 определяем по приложению А для
определяем по приложению А для  , так как для
, так как для 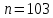
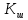 не определен
не определен
Определяем крайнее значение, которое имеет максимальную разность
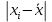
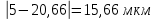
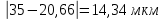
Проверяем крайнее значение 5 мкм.
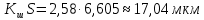
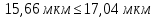
Значение 5 мкм не является промахом.
Значение 35 мкм также не является промахом, так как
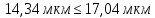
Таким образом, с обоих концов ранжированного ряда результатов измерений не осталось промахов.
Дальнейший пересчет среднего и СКО не требуется.
2. Для исправленной выборки определяем эмпирическую (статистическую) вероятность попадания случайной измеряемой величины в
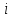 -й интервал (частость) по формуле
-й интервал (частость) по формуле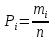
где
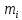 ‒ число значений, попавших в 1-й интервал;
‒ число значений, попавших в 1-й интервал;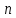 ‒ общее число экспериментальных данных.
‒ общее число экспериментальных данных.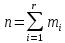
где
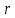 ‒ число интервалов.
‒ число интервалов.Отобразим расчеты в таблице 6.
Таблица 6 – Расчет частностей
| Номер интервала 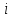 | Абсолютная частота 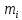 | Относительная частота 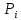 |
| 1 | 8 | 0,0777 |
| 2 | 14 | 0,1359 |
| 3 | 20 | 0,1942 |
| 4 | 32 | 0,3107 |
| 5 | 24 | 0,2330 |
| 6 | 5 | 0,0485 |
| Сумма | 103 | 1 |
Строим гистограмму, которая представляет собой ступенчатую фигуру, состоящую из прямоугольников. Основанием каждого прямоугольника являются отрезки, отображающие ширину интервала
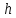 вариационного ряда, а высоты равны значениям эмпирических частостей.
вариационного ряда, а высоты равны значениям эмпирических частостей.Гистограмма изображена на рисунке 8.
Размах колебаний измеренной величины:
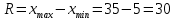
где
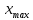 ,
, 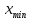 – крайние значения вариационного ряда.
– крайние значения вариационного ряда.Ширина интервала
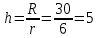
3. Определяем теоретическую вероятность попадания значений измеряемой величины в
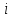 -й интервал в соответствии с законом нормального распределения:
-й интервал в соответствии с законом нормального распределения: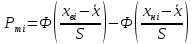
где
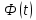 – значение функции Лапласа по приложению Б.
– значение функции Лапласа по приложению Б.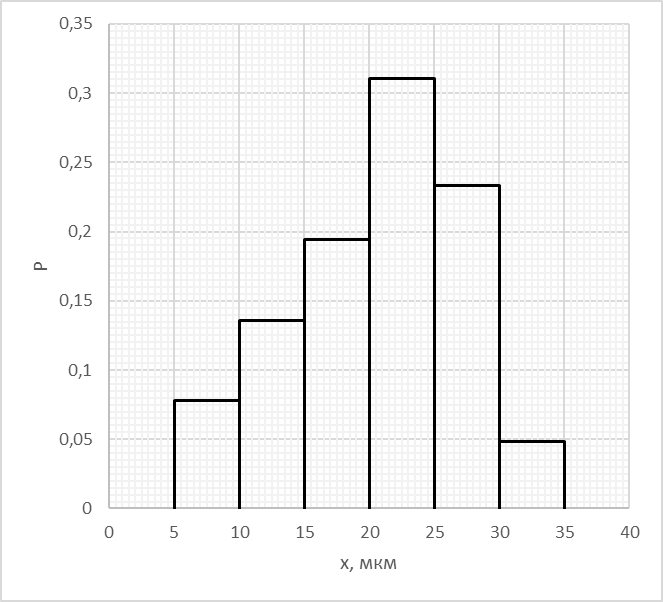
Рисунок 7 – Гистограмма эмпирического распределения
При этом следует учесть, что функция Лапласа нечетная
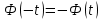
Рассчитываем для каждого интервала значение
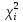
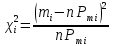
Результаты расчетов представляем в таблице 7 по установленной форме.
Наносим полученные значения теоретической вероятности на график гистограммы и строим кривую теоретического распределения вероятности по нормальному закону (рис. 9).
Таблица 7 – Расчетные данные для проверки гипотезы о нормальности распределения
| Номер интервала 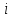 | Границы интервала | Абсолютная частота 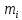 | Относительная частота 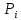 | Квантиль для границы | Функция Лапласа для границы | Теоретическая вероятность 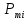 | 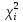 | |||
| нижняя 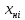 | верхняя 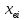 | нижней 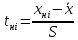 | верхней 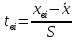 | нижней 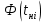 | верхней 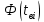 | |||||
| 1 | 5 | 10 | 8 | 0,0777 | -2,371 | -1,614 | -0,4911 | -0,4467 | 0,0444 | 2,568 |
| 2 | 10 | 15 | 14 | 0,1359 | -1,614 | -0,857 | -0,4467 | -0,3043 | 0,1424 | 0,030 |
| 3 | 15 | 20 | 20 | 0,1942 | -0,857 | -0,100 | -0,3043 | -0,0398 | 0,2645 | 1,926 |
| 4 | 20 | 25 | 32 | 0,3107 | -0,100 | 0,657 | -0,0398 | 0,2444 | 0,2842 | 0,254 |
| 5 | 25 | 30 | 24 | 0,2330 | 0,657 | 1,414 | 0,2444 | 0,4213 | 0,1769 | 1,833 |
| 6 | 30 | 35 | 5 | 0,0485 | 1,414 | 2,171 | 0,4213 | 0,4850 | 0,0637 | 0,371 |
| Сумма | - | - | 103 | 1 | - | - | - | - | 0,9761 | 6,982 |
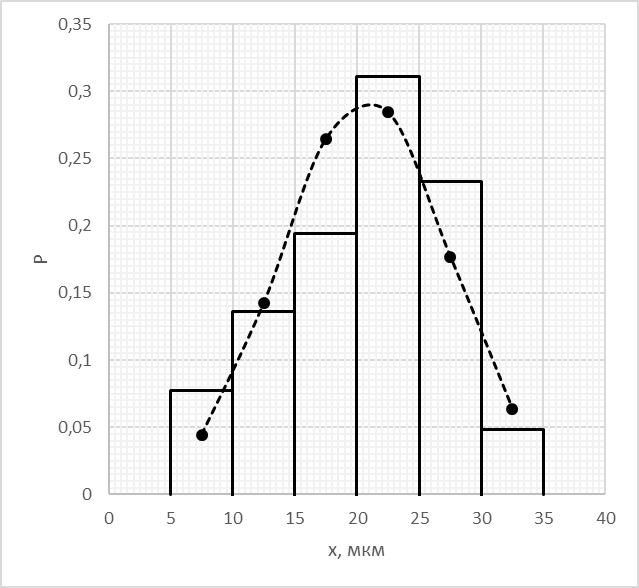
Рисунок 8 – Гистограмма эмпирического распределения и кривая теоретического распределения вероятности (пунктир)
Рассчитываем эмпирическое значение
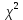
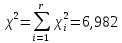
По приложению В для уровня значимости
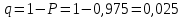
и числа степеней свободы
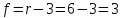
получаем табличное значение
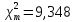
Так как
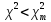 , то гипотеза о соответствии эмпирического распределения теоретическому нормальному распределению принимается.
, то гипотеза о соответствии эмпирического распределения теоретическому нормальному распределению принимается.Среднеквадратичное отклонение среднего значения
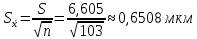
При заданной доверительной вероятности
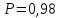 и числе степеней свободы
и числе степеней свободы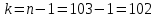
коэффициент Стьюдента по приложению Д.
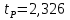
Расчет доверительного интервала
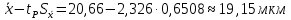
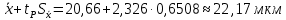
Получаем доверительный интервал
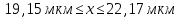
Задача 3
Дано. Произведены многократные измерения двух параметров
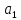 и
и  . Известна функциональная зависимость
. Известна функциональная зависимость 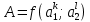 для определения косвенно измеряемой величины. Значения параметров
для определения косвенно измеряемой величины. Значения параметров 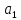 и
и  приведены в таблице 8.
приведены в таблице 8.Функциональная зависимость
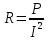
Таблица 8 – Результаты многократных измерений аргументов
| Параметр | Значения | |||||||||
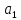 | 8,9 | 8,8 | 9,5 | 9,2 | 8,5 | 8,7 | 8,9 | 9,3 | 9,1 | 9,2 |
 | 16,2 | 16,5 | 16,0 | 16,4 | 15,7 | 15,9 | 15,8 | 16,0 | 16,3 | 15,5 |
Требуется. Найти измеряемую косвенно с помощью функциональной зависимости величину и представить результат измерений в форме доверительного интервала с доверительной вероятностью
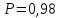 .
.Решение.
Взаимосвязи между параметрами мощности, напряжения, силы тока, сопротивления нелинейные, поэтому их функциональные зависимости линеаризуем разложением в ряд Тейлора, на основании которого вычислим результат измерений.
Рассчитываем оценочное среднее арифметическое значение измеряемой величины
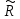 с учетом функциональной зависимости
с учетом функциональной зависимости