После окончания экспериментов, данные наблюдений показать препо­давателю.

По окончанию проведения опытов установку выключить. По выполнен­ной работе составляется отчет, содержащий:

1) номер и наименование работы;

2) краткое описание работы;

3) схему установки;

4) расчет теоретического значения критического числа оборотов вала и таблицу испытаний;

5) выводы.

Студент должен уметь объяснить полученные результаты.

---

Лабораторная работа № 4

Определение критических скоростей вращения вала с несколькими дисками
ЦЕЛЬ РАБОТЫ

1. 
   Используя приближенные методы Дункерлея и Рэлея, рассчитать первое критическое число оборотов консольного вала с 2-мя и 3-мя дисками.
   
2. 
   Экспериментально определить первое критическое число оборотов вала с 2-мя и 3-мя дисками и сравнить экспериментальные и расчетные значения.
   
3. 
   Проследить при помощи стробоскопа момент перехода вала через критическое число оборотов.
   

4.1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Вращающиеся валы машин, когда частота вращения их достигает опреде­ленной величины, становятся неустойчивыми, теряют свою прямолинейную форму, давая значительные прогибы. При дальнейшем повышении частоты вращения описанное явление прекращается, но возобновляется, когда частота вращения достигает некоторого нового значения. Частоты вращений, при кото­рых возникают эти явления, называются критическими частотами.

Рассмотрим вал с двумя дисками (рисунок 7). Пусть m₁ и m₂- массы дис­ков, e₁и e₂ - эксцентриситеты их масс, у₁и у₂ - упругие прогибы при угловой скорости w_pa6.

На вал действуют центробежные силы:
(4.1)
(4.2)

Используя коэффициенты влияния, прогибы у₁и у₂можно выразить как




Рисунок 7 - Расчетная схема вала
Обозначая


и группируя подобные члены, получим систему из двух линейных неоднород­ных уравнений с двумя неизвестными:

(4.3)
Значения неизвестных могут быть даны выражениями, в которых знаме­нателем является определитель однородной системы, а числителем - тот же оп­ределитель, в котором коэффициенты при искомом неизвестном заменены сво­бодными членами:

---

(4.4)
(4.5)
Запишем для сравнения уравнение частот для вала с двумя нагрузками:

Нетрудно видеть, что знаменателем значений у₁и у₂является уравнение частот для вала с двумя нагрузками, в котором вместо частоты свободных ко­лебаний вала wстоит w_paб будет равно одной из свободных частот колебаний вала w₁ или w₂, знаменатель обратится в нуль, и мы будем иметь у_} = у₂= , т.е. при скорости w_paб = w₁) или w₂прогибы вала будут стремиться к бесконечности, вал будет неустойчив.

Очевидно, приведенное выше рассуждение имеет вполне общий характер, и аналогичные результаты были бы получены и для валов с тремя, четырьмя и т.д. дисками.

Следует отметить вероятностный характер явления, так как для того, что­бы оно имело место, наличие начального эксцентриситета вовсе не обязатель­но. Представим себе принципиально возможный случай е₁ = е₂ = 0. Тогда y₁ =y₂=0. Однако достаточно, чтобы под влиянием случайных причин вал по­лучил сколь угодно малый прогиб, и уравнения (4.4) и (4.5) вступали в силу.

Таким образом, критическая частота вала, нагруженного массами, сосре­доточенными в точках, лежащих на оси вала, есть частота вращения, равная любой круговой частоте его собственных колебаний. Следовательно, задача определения критической частоты вала сводится к определению частоты его свободных колебаний.

Валы, вращающиеся со скоростью ниже первой критической, называются жесткими.

Если скорость вала превышает первую критическую, вал называется гиб­ким.

Как было отмечено выше, определение критической скорости валов, на­груженных сосредоточенными массами, приводит к решению уравнения час­тот, содержащего в любой части определитель, порядок которого выше числа степеней свободы системы. Если последнее невелико (не более 4-5), раскрытие определителя больших трудностей не представляет. Если же число нагрузок превышает 4-5, задача раскрытия определителя весьма осложняется.

---

В связи с этим на практике для определения критической скорости вра­щения валов часто используются приближенные методы расчета.

Рассмотрим два из этих методов; метод наложения и энергетический ме­тод Рэлея.

4.1.1 Метод наложения (метод Дункерлея)

Этот метод дает возможность определить наименьшее возможное значе­ние основной частоты. Формула Дункерлея может быть представлена в сле­дующем виде:

(4.6)

где w1

-

критическая угловая скорость ротора при наличии только одного диска.

В случае действия распределенной по какому-либо закону непрерывной нагрузки q(x) формула Дункерлея имеет вид
(4.7)

где axx

-

прогиб в точке x под действием единичной силы, приложенной в той же точке.

Интегрирование распространяется на весь интервал, на котором распре­делена нагрузка, и если таких интервалов несколько, то на все интервалы.

В общем случае действие сосредоточенных и распределенных масс будет
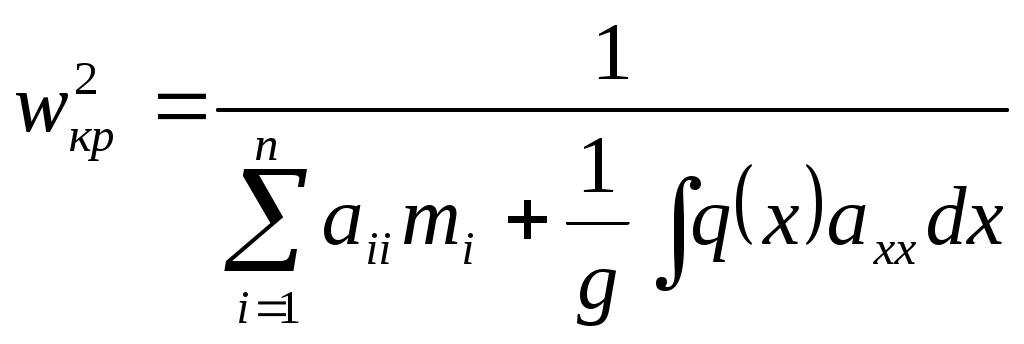(4.8)
4.1.2 Энергетический метод Рэлея

Сущность этого метода сводится к определению частоты колебаний из равенства максимальных значений потенциальной и кинетической энергии сис­темы при заранее заданной форме упругой кривой основного вида колебаний.



Рисунок 8 - Схема колеблющейся балки
Применим к колеблющейся системе принцип сохранения энергии, пред­полагая колебания без потерь;

T + V = const(4.9)

где V	-	потенциальная энергия колеблющейся системы;
Т	-	кинетическая энергия колеблющейся системы.

Если y₁, у₂ ...у_i- прогибы балки в точках приложения нагрузок в момент t

---

(рисунок 8), то ее потенциальная энергия будет:
(4.10)
а кинетическая

(4.11)
Рассмотрим случай колебания с наименьшей частотой, когда все массы одновременно достигают максимального удаления от положения покоя и еди­новременно через него проходят, накопляя в этих двух положениях максимум кинетической или потенциальной энергии. При прохождении через положение равновесия, которому соответствует недеформированное состояние вала, по­тенциальная энергия равна нулю. Так как в этом положении скорость макси­мальна, кинетическая энергия достигает значения Т_тах:
Т_тах + 0 = const(4.12)
Обратное происходит при максимальном удалении всех масс от состоя­ния покоя (линия ABC). В этот момент массы прекращают свое движение, что­бы начать обратное колебание. Скорость, а вместе с ней Т, равны нулю, а по­тенциальная энергия достигает значения V_max:
V_max+0=const=T_max (4.13)
Так как грузы совершают гармоническое колебание, то


,
Откуда







и окончательно

(4.14)
Очевидно, что , представляющие амплитуды колебания точек приложе­ния грузов, являются прогибами динамическими. Рэлей предложил заменить статическими прогибами балки, т.е. принять
(4.15)

где fi

-

статический прогиб вала под грузом Giпри нагружении ее всеми нагрузками.

---

Смотрите также файлы

• Согласие на обработку персональных данных и использование предоставляемой информации Исполнительному директору Общероссийской общественногосударственной детскоюношеской организации Российское движение школьников.docx

• Вопросы к экзамену по дисциплине экономическая теория.pdf

• Изменчивость.docx

• Курсовая работа должна содержать исходные данные.docx

• Пні Химия за мерзімді жоспар блімі.doc