Лабораторная работа № 3

Определение критических скоростей вращения вала с одним диском
ЦЕЛЬ РАБОТЫ

Определение критической частоты вращения вала с одним диском теоре­тическим и экспериментальным путем, сравнение результатов.
3.1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Понятие о критическом числе оборотов вала. Определение первой крити­ческой скорости вращения вала.

Критические скорости вращения валов были обнаружены в середине XIX века в связи с увеличением быстроходности различных машин, содержащих роторы, состоящие из вала с насаженными на него дисками или другими мас­сивными телами. Такие роторы имеются в турбинах, турбокомпрессорах, цен­трифугах, редукторах. Достигнув определенной скорости вращения, вал с дис­ками начинает колебаться, давая значительные, постепенно нарастающие про­гибы. При этом сильно возрастают дисбалансы вращающихся масс, вследствие чего машина в целом испытывает сильные вибрации. Значительно возрастают нагрузки на подшипники, станину и фундамент. При дальнейшем повышении частоты вращения колебания ротора прекращаются и возобновляются, когда скорость достигает некоторого нового значения. Скорости вращения, при кото­рых возникают опасные для работы машин колебания валов, называются кри­тическими. При критических скоростях амплитуды колебаний становится весь­ма большой; вал испытывает значительные динамические прогибы и соответст­венно большие напряжения. Длительная работа вала с дисками при критиче­ской скорости недопустима, так как прогибы и напряжения возрастают до та­кой степени, что вал разрушается (получает остаточные деформации). Однако постепенность нарастания амплитуды колебаний (прогиба) дает возможность кратковременно работать при критической скорости вращения. В связи с этим в период разгона машины, при достаточно быстром росте скорости, можно миновать критическую скорость и работать в сверхкритической области.

Критические явления носит резонансный характер: критическая частота вращения вала совпадает с частотой собственных изгибных колебаний того же вала. Вал совершает эти колебания даже при отсутствии вращения, если дейст­вием каких-либо сил его изогнуть, а затем предоставить самому себе.

В связи с опасностью разрушения вала при критической частоте враще­ния, задача ее определения является весьма важной.

---

Хотя при обработке вала и дисков стремятся добиться, возможно, более точной их балансировки, однако точного совпадения центра тяжести ротора с геометрической осью вала можно достигнуть лишь случайно. Обычно центр тяжести имеет некоторый эксцентриситет, который, как бы мал он не был, вы­зывает центробежную силу, тем большую, чем выше частота вращения вала.

Рассмотрим действие этой силы на вал с одним диском. Ось вала выберем вертикальной, чтобы не учитывать влияние собственной массы вала. Допустим, что вал абсолютно упругий и при определенной скорости может получить не­ограниченный прогиб (рисунок 4).

Определим прогиб вала под действием центробежной силы вращающейся массы диска.

Пусть т - масса диска, е - эксцентриситет его центра тяжести относи­тельно оси вала.
На вал действует центробежная сила
(3.1)

где т	-	масса диска, кг;
r	-	радиус вращения центра масс (точки О), м;
w	-	угловая скорость вращения вала, с-1.

Первоначально r= е, но после того, как вал получит упругий прогиб у, радиус вращения станет равным r = е + у и центробежная сила
(3.2)
Центробежная сила F_цб’ стремится переместить точку по радиусу от оси вращения; этому движению препятствует сила упругости, действующая на точку со стороны вала и пропорциональная его прогибу:
F_упр = k·y, (3.3)


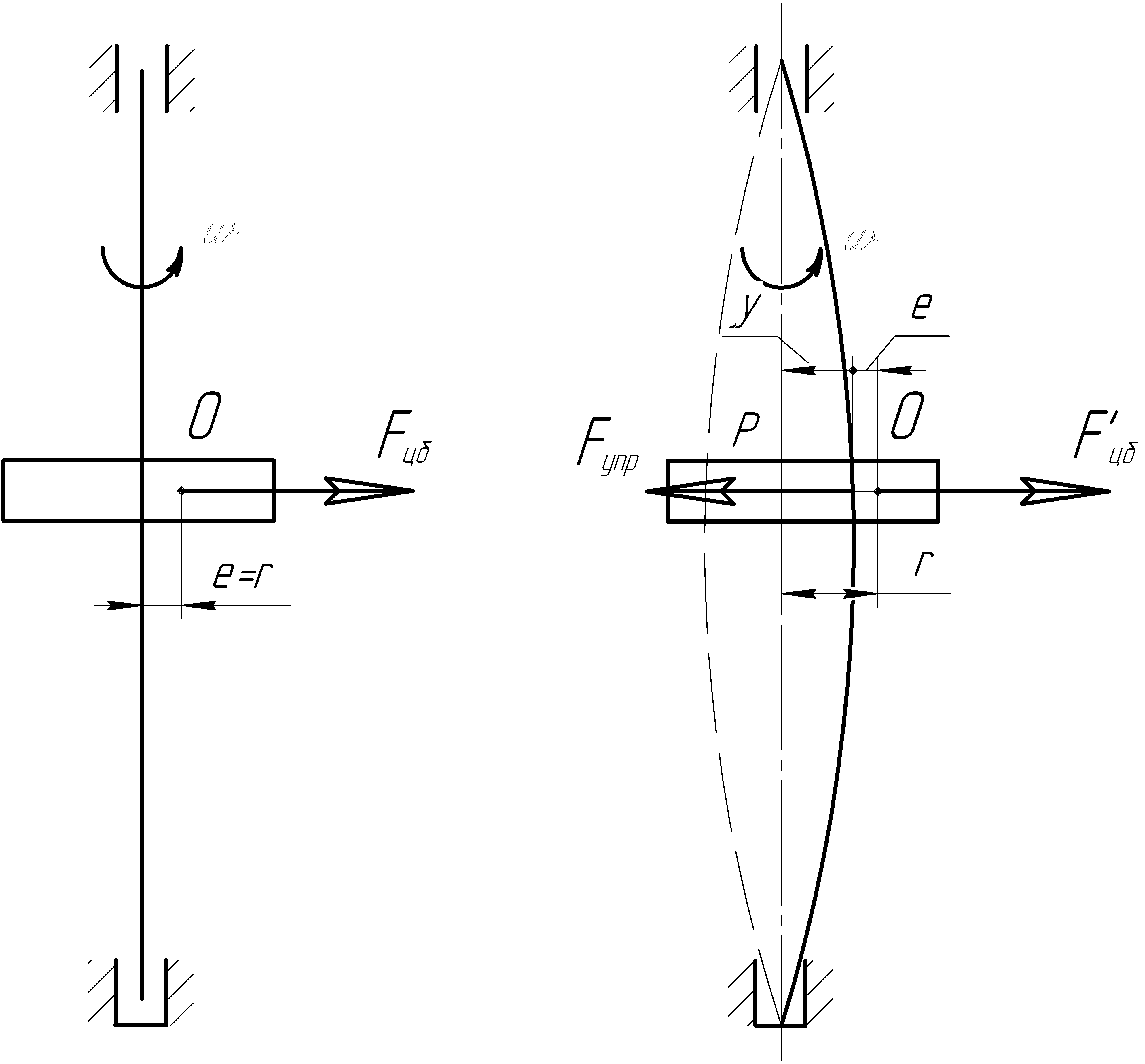
Рисунок 4 - Расчетная схема вала
Коэффициент пропорциональности к представляет собой силу, вызы­вающую единичный (т.е. равный 1 см) прогиб, и характеризует изгибную жесткость вала. Размерность коэффициента пропорциональности - Н/м. Других сил, действующих на массу, нет; по­этому уравнение равновесия сил, действующих на нее, имеет вид



или

m(e+y)w²=ky, (3.4)
Из этого уравнения легко найти зависимость прогиба от скорости враще­ния

---

wи начального эксцентриситета е:
(3.5)
При определенном значении угловой скорости выражение k - m·w², стоя­щее в знаменателе, обращается в нуль. При этом прогиб становится бесконеч­ным. Это значение угловой скорости и является критическим:
(3.6)
(3.7)
Более удобный вариант формулы (3.7) содержит так называемый "стати­ческий прогиб" f. Приложим мысленно к валу в направлении, перпендикулярном его оси, силу, равную весу диска G = mg. Аналогично уравнению (3.7) будем иметь

G = m·g =k·f,(3.8)

где f	-	статический прогиб;
k	-	сила, вызывающая единичный прогиб;
g	-	ускорение свободного падения, м/с2.

Определив из уравнения (3.8) величину kи подставив её в уравнение (3.7), получим

. (3.9)
На основании уравнения (3.9) можно заключить, что критическая угловая скорость зависит от ускорения силы тяжести g. В действительности это не так. Дело в том, что пропорционально ускорениюсилы тяжести изменяется fи отношение g/fостается постоянным.

Реально при критической скорости вращения прогиб вала не становится бесконечно большим, но может достичь опасной величины. Здесь играет роль неабсолютная упругость материала вала, сопротивление среды и другие причи­ны, приводящие к рассеиванию энергии при изгибе или колебаниях и объединяемых обычно понятием "затухание".

Анализ влияния величины начального эксцентриситета е на прогиб при вращении позволяет обнаружить вероятностный или неустойчивый характер явления. Для того чтобы критическое явление имело место, наличие начально­го эксцентриситета не обязательно.

Существенно то, что при критической скорости вращения прогиб неогра­ниченно возрастает. При е = 0, согласно уравнению (3.5), прогибу = 0 при лю­бой скорости вращения. Однако достаточно, чтобы под влиянием случайных причин вал получил весьма малый прогиб, и при

---

w=w_k прогиб становится бес­конечно большим.

В случае вала с одним диском можно обнаружить явление самоцентриро­вания. Для этого найдем предел, к которому стремится прогиб вала при неогра­ниченном возрастании скорости вращения. Разделив числитель и знаменатель дроби в правой части уравнения (3.5) на w - w², получим

,

при ; и

Физически это означает: вал изгибается таким образом, что центр тяже­сти приближается к оси вращения. При этом радиус вращения центра тяжести r = е + у, а с ним и центробежная сила, возбуждающая колебания вала, значи­тельно уменьшается. Полного самоцентрирования (т.е. равенства у = -е) практически достичь невозможно, так как нельзя достичь бесконечной скорости вращения.

Определение критической частоты вращения вала с помощью энергети­ческого метода Рэлея.

В большинстве случаев валы имеют переменный по длине диаметр и на­гружены дисками. Для определения первой критической частоты вращения та­кого вала можно пользоваться методом Рэлея.

Частоту собственных колебаний по энергетическому методу находят из условий равенства потенциальной и кинетической энергии ротора за период колебания. В любой момент времени колеблющаяся балка обладает как кине­тической, так и потенциальной энергией; при этом в процессе колебания про­исходит непрерывное превращение одного вида энергии в другой. Кинетиче­ская энергия представляет собой энергию движения имеющихся на балке масс. Потенциальная энергия связана с изгибом балки и обусловлена силами упруго­сти, стремящимися вернуть её в положение равновесия. Если потери при коле­баниях отсутствуют, то согласно принципу сохранения энергии, полная энергия остается постоянной

T + V = const, (3.10)

где Т	-	кинетическая энергия;
V	-	потенциальная энергия.

Вполне удовлетворительный по точности результат получается, если за кривую прогиба вала принять его упругую линию

---

, обусловленную действием статической нагрузки.

Пусть сила тяжести дисков составляет G₁, G₂, G₃; прогибы под дисками Y₁, Y₂, Y₃.

Потенциальная энергия деформации вала, накапливаемая за время мак­симального отклонения его от положения равновесия:
(3.11)
Расстояние центров тяжести дисков от положения равновесия в любой момент во времени колебания равны:
y₁ = sin wt;

y₂=sin wt;

у₃=sin wt,

где w	-	круговая частота колебаний;
t	-	время.

Когда диски проходят через положение равновесия, скорости их дости­гают наибольшего значения:



Кинетическая энергия ротора в этот момент максимальна, а потенциаль­ная энергия равна нулю:
(3.12)

где m, m₁ , m₂, m₃ - массы вала и его частей.
Формулы (3.11) и (3.12) определяют максимальные (за время колебания) значения потенциальной и кинетической энергии. Приравнивая их друг к другу, определяем круговую частоту колебаний, т.е. критическую угловую скорость:
(3.13)
а критическая частота вращения:
(3.14)
Если балка нагружена непрерывно распределенной нагрузкой на единицу длины q - q(x), уравнение (3.13) имеет вид
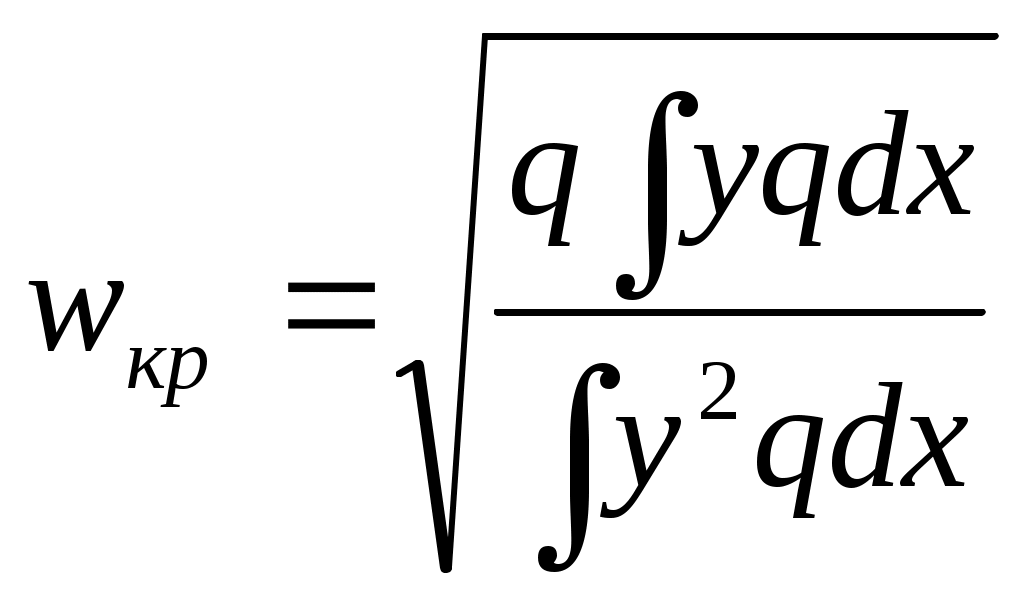, (3.15)
где у = у(х) - уравнение упругой линии балки.
Если одновременно действуют сосредоточенные и распределенные на­грузки, уравнение Рэлея имеет вид:
. (3.16)
Графоаналитический способ определения первой критической скорости вала переменного сечения

---

Смотрите также файлы

• Согласие на обработку персональных данных и использование предоставляемой информации Исполнительному директору Общероссийской общественногосударственной детскоюношеской организации Российское движение школьников.docx

• Вопросы к экзамену по дисциплине экономическая теория.pdf

• Изменчивость.docx

• Курсовая работа должна содержать исходные данные.docx

• Пні Химия за мерзімді жоспар блімі.doc