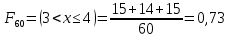Файл: Задача Игральная кость подбрасывается дважды. Какова вероятность того, что число очков, выпавших первый раз большего числа очков, выпавших на второй кости. Решение.docx
Добавлен: 28.04.2024
Просмотров: 13
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача 1.
Игральная кость подбрасывается дважды. Какова вероятность того, что число очков, выпавших первый раз большего числа очков, выпавших на второй кости.
Решение
Поскольку кость имеет шесть ребер, мы будем отталкиваться от того, что игральная кость имеет 6 возможных исходов при подбрасывании. По правилу произведения в комбинаторике, при двух подбрасываниях игральной кости число равновозможных исходов будет равно:
Количество всевозможных подбрасывания двух игральных костей равно
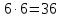 из них благоприятствуют те, у которых на первой игральной кости число очков больше, чем на второй:
из них благоприятствуют те, у которых на первой игральной кости число очков больше, чем на второй:1) Если на первой игральной кости выпало 1, то на второй: {2;3;4;5;6} - 5 вариантов
Если выпало 2 очка, то на второй кости: {3;4;5;6} - 4 варианта
Если выпало 3 очка, то на второй кости: {4;5;6} - 3 варианта
Если выпало 4 очка, то на второй кости: {5;6} - 2 варианта
Если выпало 5 очков, то на второй кости: {6} - 1 вариант
Всего вариантов: 5+4+3+2+1=15
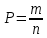
где m - число благоприятных исходов; n - число всевозможных исходов
m = 15; n = 36;
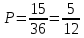
Задача 2.
10. Рабочий обслуживает 3 станка. Вероятность брака для первого станка равна – 0.01, для второго – 0.03, для третьего – 0.04. Производительность всех станков одинакова. Изготовленные детали попадают на общий конвейер. Определить вероятность того, что взятая на удачу деталь будет годной.
Решение
Рассмотрим 3 гипотезы по данной задаче:
Hi = {деталь изготовлена на i – ом станке}, i = 1, 2, 3.
Пусть x – производительность третьего станка, тогда 2x – производительность второго станка, 6x – производительность первого станка. Так как вероятность гипотез пропорциональна производительностям соответствующих станков, то можно считать, что:

Следовательно,

Рассмотрим событие A = {взятая деталь - бракованная}. Условные вероятности события А известны.

Формула полной вероятности
-
Теорема -
Если события
-
Образуют полную группу и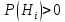 то для любого события А справедлива формула:
то для любого события А справедлива формула: 

По формуле полной вероятности имеем:
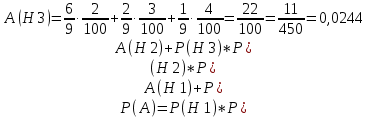
Задача 3.
Задан закон распределения дискретной случайной величины Х и значения
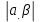
1. Найти математическое ожидание, среднее квадратическое отклонение и моду с.в. Х
2. Записать функцию распределения с.в. Х.
3. Найти вероятности с.в.

Условие: α = 0, β = 3
| Х: | -1 | 0 | 1 |
| | 0,6 | 0,2 | 0,2 |
Решение
Найдем математическое ожидание, среднее квадратическое отклонение и модуль случайно величины Х.
Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений хi, которые принимает случайная величина Х, на соответствующие вероятности pi:
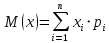
Отсюда находим математическое ожидание М[X]:
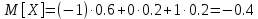
Дисперсию находим по формуле:
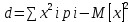
Дисперсия D|X|:

Среднее квадратическое отклонение σ(x):
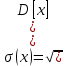
Функция распределения F(X):
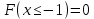
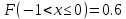
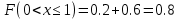
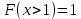
Вероятность попадания СВ в тот ли иной интервал находится по формуле:
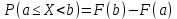
Найдем вероятность того, что СВ будет находиться в интервале
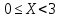

Вероятность попадания СВ в тот ли иной интервал находится по формуле:
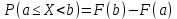 Найдем вероятность того, что СВ будет находиться в интервале
Найдем вероятность того, что СВ будет находиться в интервале 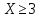
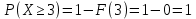
Задача 4.
Задана f(x) – плотность распределения непрерывной случайной величины Х.
1. Найти с.
2. Найти математическое ожидание и дисперсию с.в. Х.
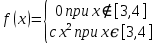
Решение:
Начнем с того, что найдем параметр с из условия:
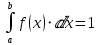
Теперь запишем такое же уравнение, но уже для нашей функции:


Или
 , откуда А =
, откуда А = 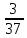
Функция распределения:
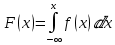
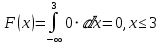
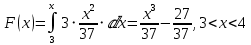
F(x) = 1, x > 4
Математическое ожидание:
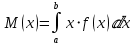
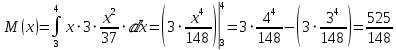
Дисперсия:
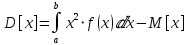 2
2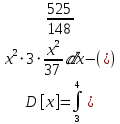 2 =
2 = 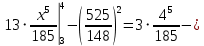

Задача 5.
В партии из 15 деталей 3 бракованных. Наугад выбирают 6 изделий, с возращением каждый раз вынутого изделия обратно. Определить вероятность того, что среди этих изделий нет бракованных.
Решение
Для вычисления события А (среди деталей нет бракованных) воспользуемся формулой,
 , где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события А. В нашем случае общее число возможных исходов элементарных исходов равно числу способов, которыми можно извлечь 6 деталей и 15 имеющихся, то есть
, где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события А. В нашем случае общее число возможных исходов элементарных исходов равно числу способов, которыми можно извлечь 6 деталей и 15 имеющихся, то есть 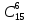 . А общее благоприятствующих исходов равно числу способов, которыми можно извлечь 6 не бракованных деталей из 12, то есть
. А общее благоприятствующих исходов равно числу способов, которыми можно извлечь 6 не бракованных деталей из 12, то есть 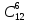 . Следовательно,
. Следовательно, 
Задача 6.
Вероятность попадания в цель при одном выстреле равна p. Выстрелы производятся в независимости друг от друга. С.в. Х показывает число попаданий при nвыстрелов.
1. Найти математическое ожидание, дисперсию, моду с.в. Х.
2. Найти
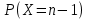
3. Найти вероятности
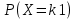
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P | 0,5 | 0,6 | 0,7 | 0,6 | 0,8 | 0,9 | 0,4 | 0,3 | 0,6 | 0,3 |
| N | 5 | 6 | 7 | 8 | 5 | 6 | 7 | 8 | 4 | 3 |
| K1 | 3 | 4 | 5 | 2 | 4 | 5 | 2 | 3 | 1 | 0 |
Случайная величина Х распределена биноминально с параметрами
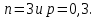
1) Найдем математическое ожидание и дисперсию случайной величины Х:
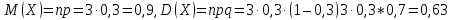
Мода m = Mo(X) случайной величины X есть ее наиболее вероятное значение, которое является целочисленным решением неравенства
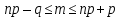
Имеем:
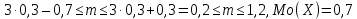
2,3) Найдем вероятности

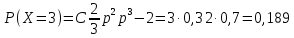

Задача 9.
По заданному распределению выборки:
| Xi | X1 | X2 | X3 | X4 | …. |
| Ni | N1 | N2 | N3 | N4 | …. |
1) Записать эмпирическую функцию распределения;
2)Найти выборочную среднюю
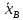 и выборочную дисперсию
и выборочную дисперсию 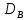 .
.| Xi | 2 | 3 | 4 | 5 |
| Ni | 15 | 14 | 15 | 16 |
Решение
1) в таблице значение
 , т.е.
, т.е. 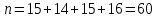
Далее вычисляем функцию распределения выборки