ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.04.2024
Просмотров: 126
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 3. Преобразуйте двоичные числа в восьмеричные и шестнадцатеричные.
| № варианта | | № варианта | |
| 1 | 100000111 | 6 | 101011101 |
| 2 | 100100101 | 7 | 111000101 |
| 3 | 101010100 | 8 | 111100111 |
| 4 | 110111001 | 9 | 100111010 |
| 5 | 100010011 | 10 | 110010001 |
Задание 4. Переведите в двоичную систему десятичные числа.
| № варианта | | № варианта | |
| 1 | 0,625 | 6 | 0,75 |
| 2 | 0,28125 | 7 | 7/16 |
| 3 | 0,078125 | 8 | 3/8 |
| 4 | 0,34375 | 9 | 1/4 |
| 5 | 0,25 | 10 | 0,515625 |
3. Содержание отчета.
Отчет должен содержать:
-
Название работы. -
Цель работы. -
Задания 1-4 и их решение. -
Вывод по работе.
4. Контрольные вопросы
-
Что такое система счисления? -
Что такое основание системы счисления? -
Что такое непозиционная система счисления? -
Что такое позиционная система счисления? -
Из каких знаков состоит алфавит десятичной и двоичной систем? -
Почему в вычислительной технике взята за основу двоичная система счисления? -
Какое наибольшее десятичное число можно записать тремя цифрами:
-
в двоичной системе; -
в восьмеричной системе; -
в шестнадцатеричной системе?
Практическая работа №5
Тема: Реализация логических операций средствами элементарных схем.
Цель: научиться составлять аналитические выражения по табличному значению функции, строить схемы из элементарных логических элементов по заданному аналитическому выражению функции.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Изучите краткие теоретические сведения. Рассмотрите примеры решения заданий.
1. Логические элементы
Функция отрицание НЕ или инверсия
Таблица истинности функции отрицания имеет вид:
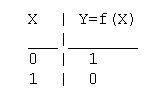
Логический элемент НЕ обозначается на схемах следующим образом:
(пишется X c чертой сверху)
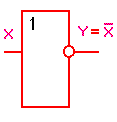
Логическое ИЛИ (логическое сложение, дизъюнкция): Y= X1 + X2 = X1VX2
Таблица истинности логического ИЛИ имеет вид:
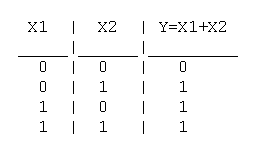
Логический элемент ИЛИ обозначается на схемах следующим образом:
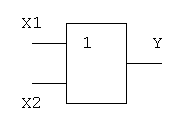
Логическое И (логическое умножение, конъюнкция): Y = X1X2 = X1&X2
Таблица истинности логического И имеет вид:
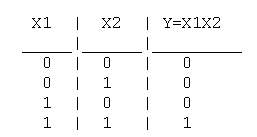
Логический элемент И обозначается на схемах следующим образом:
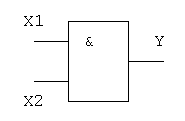
Функция ИЛИ-НЕ: Y = (X1+X2)
Таблица истинности функции ИЛИ-НЕ имеет вид:
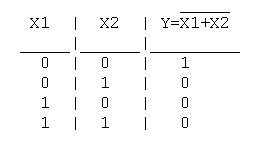
Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом:
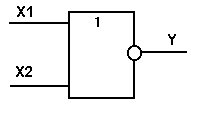
Функция И-НЕ: Y = (X1^X2)
Таблица истинности функции И-НЕ имеет вид:
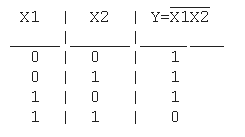
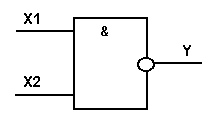
Логический элемент И-НЕ обозначается на схемах следующим образом:
2. Алгоритм построения логических схем.
-
Определить число логических переменных. -
Определить количество базовых логических операций и их порядок. -
Изобразить для каждой логической операции соответствующий ей вентиль. -
Соединить вентили в порядке выполнения логических операций.
Пример 1.
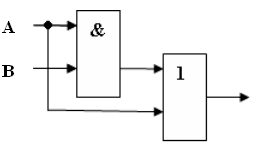
Составить логическую схему для логического выражения: F=A v B & A.
Две переменные – А и В.
Две логические операции: 1-&, 2-v.
Строим схему:
2. Практическая часть. Выполните задания.
Задание 1
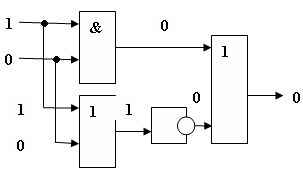
Постройте логическую схему, соответствующую логическому выражению F=А&Вv (ВvА). Вычислить значения выражения для А=1,В=0.
Переменных две: А и В;
Логических операций три: & и две v; А&Вv (Вv А).
Схему строим слева направо в соответствии с порядком логических операций:
Построить логические схемы по формулам и составить таблицу истинности
Вариант 1
а) F= (AvB)&(CvB)
б) F= (A&B&C)
Вариант 2
а) F=(A&B)vC.
б) F=A&BvC.
В ариант 3
а)F= (AvB) & (AvB).
б)F= ((AvB) & (AvB)) & (AvB).
Вариант 4
а) F= A&B&C&D.
б) F= (AvB) &(AvB).
Задание 2
По табличному заданию функции найти аналитическое выражение функции и построить логическую схему в соответствии со своим вариантом.
1) А и В или С и D
2) (А или В) и (А или С)
3) А и (В или С)
4) А или (не В или не С)
5) не (не A и не (B и C))
Задание 3
1) А и А или В и (А и В или В)
2) ((А или В) => В) и (А или В)
3) А и В <=> (A или B)
4) А и B и (А и В)
5) A и (B и (А или В))
ПРАКТИЧЕСКАЯ РАБОТА:
Задание 1:
Задание 2:
Пусть А = «Ане нравятся уроки математики», а В = «Ане нравятся уроки химии». Выразите следующие формулы на обычном языке:
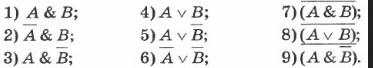
Задание 3:
Постройте таблицы истинности для следующих логических выражений:

Задание 4:
Упростите сложное логическое выражение, основываясь на логические
законы:
1 (¬А В) (¬А В) ¬ (А В)
2 ¬ (А В ¬С)
3 А В С А ¬С А В
4 А ¬В А В С А ¬(В С)
Задание 5:
1) Разбирается дело Джона, Брауна и Смита. Известно, что один из них нашёл и утаил клад. На следствии каждый из подозреваемых сделал два заявления:
Смит: «Я не делал этого. Браун сделал это».
Джон: «Браун не виновен. Смит сделал это».
Браун: «Я не делал этого. Джон не делал этого».
Суд установил, что один из них дважды солгал, другой дважды сказал правду, третий один раз солгал, один раз сказал правду. Кто из подозреваемых должен быть оправдан?
2) Алёша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения:
Алеша: «Это сосуд греческий и изготовлен в V веке».
Боря: «Это сосуд финикийский и изготовлен в III веке».
Гриша: «Это сосуд не греческий и изготовлен в IV веке». Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
3) Задача "Лига чемпионов"
Четыре футбольных клуба: итальянский ФК «Рома», испанская – ФК «Барселона», российская – ФК «Зенит», английская – ФК «Арсенал» встретились в групповом этапе лиги чемпионов по футболу. Их тренировали тренеры из этих же четырех стран: итальянец Адриано, испанец Жозе, русский Владимир, англичанин Генри. Известно, что национальность у всех четырех тренеров не совпадала с национальностью команд. Требуется определить тренера каждой команды, если известно:
ФК «Зенит» не тренируется у Генри и Адриано.
ФК «Рома» обещал никогда не брать Генри главным тренером.
Контрольные вопросы.
1. Что изучает наука логика?
2. Перечислите и опишите известные вам формы мышления.
3. Опишите и составьте таблицы истинности для известных вам логических функций.
4. Нарисуйте условное обозначение и таблицы истинности для известных вам логических элементов.
5. Как производится синтез комбинационных устройств?
Практическая работа №6
Тема: Решение задач алгоритмической структуры
Цель: усвоить понятия: алгоритм как фундаментальное понятие информатики, способы описания, основные типы алгоритмов, освоить принципы решения задач с использованием основных алгоритмических конструкций.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Изучите краткие теоретические сведения. Рассмотрите примеры решения заданий.
Решение любой задачи на ЭВМ можно разбить на следующие этапы: разработка алгоритма решения задачи, составление программы решения задачи на алгоритмическом языке, ввод программы в ЭВМ, отладка программы (исправление ошибок), выполнение программы на ПК, анализ полученных результатов.
Первый этап решения задачи состоит в разработке алгоритма.
Алгоритм – это точная конечная система правил, определяющая содержание и порядок действий исполнителя над некоторыми объектами (исходными и промежуточными данными) для получения после конечного числа шагов искомого результата.
Алгоритм может быть описан одним из трех способов:
-
словесным (пример в начале раздела); -
графическим (виде специальной блок-схемы); -
с помощью специальных языков программирования.
Блок-схема – распространенный тип схем, описывающий алгоритмы или процессы, изображая шаги в виде блоков различной формы, соединенных между собой стрелками.
-
Линейный алгоритм – это такой алгоритм, в котором все операции выполняются последовательно одна за другой. -
Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие. -
Алгоритмы циклической структуры.
Циклом называют повторение одних и тех же действий (шагов). Последовательность действий, которые повторяются в цикле, называют телом цикла.
Циклические алгоритмы подразделяют на алгоритмы с предусловием, постусловием и алгоритмы с конечным числом повторов. В алгоритмах с предусловием сначала выполняется проверка условия окончания цикла и затем, в зависимости от результата проверки, выполняется (или не выполняется) так называемое тело цикла.
Пример 1. Определить площадь трапеции по введенным значениям оснований (a и b) и высоты (h).
| Запись решения задачи на алгоритмическом языке: алг трапеция вещ a,b,h,s нач ввод f,b,h s:=((a+b)/2)*h вывод s кон | Запись алгоритма в виде блок-схемы: 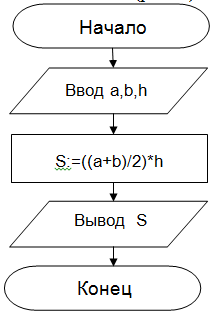 |
Пример 2. Определить среднее арифметическое двух чисел, если a положительное и частное (a/b) в противном случае.
| Запись решения задачи на алгоритмическом языке: алг числа вещ a,b,c нач ввод a,b если a>0 то с:=(a+b)/2 иначе с:=a/b все вывод с кон | Запись алгоритма в виде блок-схемы: 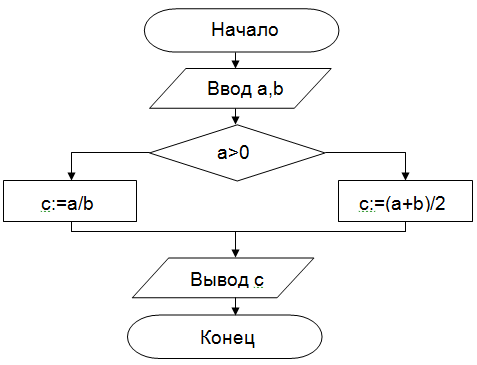 |
Пример 3. Составить алгоритм нахождения суммы целых чисел в диапазоне от 1 до 10.
| Запись решения задачи на алгоритмическом языке: алг сумма вещ a,s нач S:=0; A:=1; нц пока a<=10 S:=S+a; A:=a+1; кц вывод S кон | Запись алгоритма в виде блок-схемы: 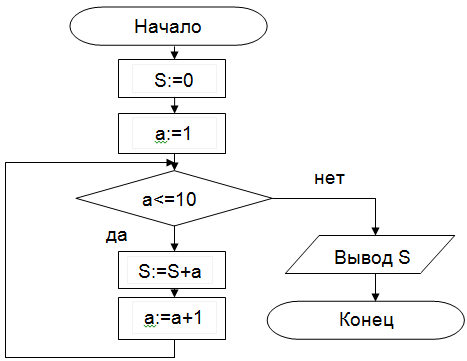 |
В алгоритме с постусловием сначала выполняется тело цикла, а затем проверяется условие окончания цикла. Решение задачи нахождения суммы первых десяти целых чисел в данном случае будет выглядеть следующим образом:
| Запись решения задачи на алгоритмическом языке: алг сумма вещ a,s нач S:=0; A:=1; нц S:=S+a; A:=a+1; пока a<=10 кц вывод S кон | Запись алгоритма в виде блок-схемы: 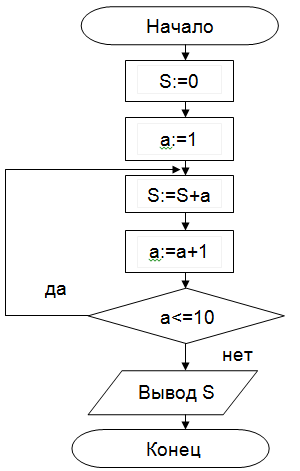 |
2. Практическая часть. Задания
Вариант 1 Вариант 2
-
Найдите значения переменной S после выполнения программы
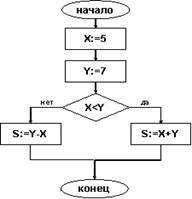 | 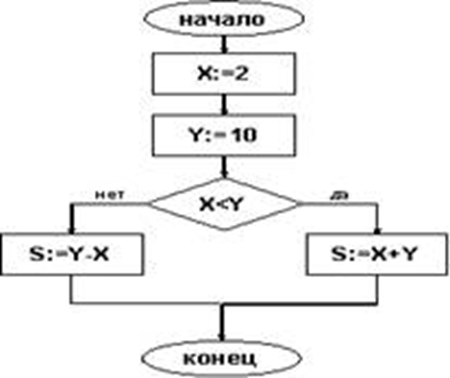 |
| 2. Найдите значения переменной y после выполнения программы | |
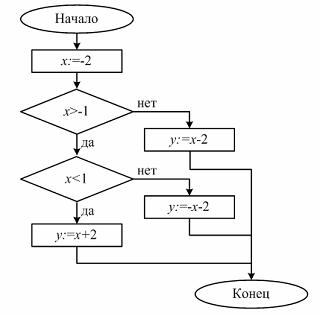 | 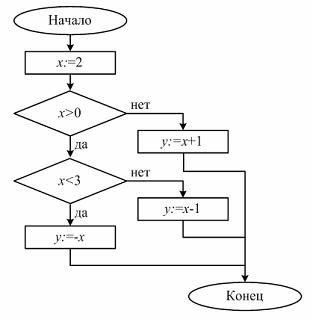 |
| 3. Найдите значения переменной C после выполнения программы | |
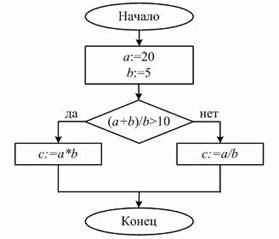 | 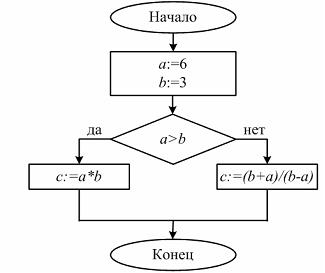 |
| 4. Выполни алгоритм для числа х=11 : | 4. Выполни алгоритм для числа х=14 : |
