Файл: Перечень вопросов к зачёту по дисциплине Воздушная навигация и аоп.docx

ПЕРЕЧЕНЬ ВОПРОСОВ К ЗАЧЁТУ по дисциплине «Воздушная навигация и АОП»

1. Форма и размеры Земли.

Уровенная поверхность – поверхность, во всех точках перпендикулярная направлению силы тяжести (отвесной линии).

В качестве сглаженной фигуры Земли разумно выбрать форму уровенной поверхности, совпадающей с физической поверхностью в морях и океанах, где нет неровностей рельефа. Такая фигура получила название геоида

---

.

Геоид – фигура, образованная уровенной поверхностью, совпадающей в морях и океанах с их средней поверхностью.

В районах материков поверхность геоида проходит под уровнем рельефа местности. Эта поверхность называется средним уровнем моря, от которого отсчитывается высота рельефа и другие высоты.



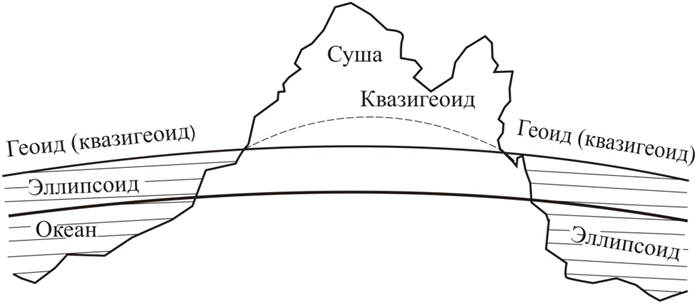
В России за начало уровня отсчета высот принято нулевое деление футштока (мерной линейки), установленной в Обводном канале г. Кронштадта.

Для удобства навигационных расчетов форму Земли представляют в виде шара с незначительным сжатием у полюсов. Этот эллипс имеет следующие размеры: экваториальный радиус а = 6378 км, полярный радиус b = 6357 км



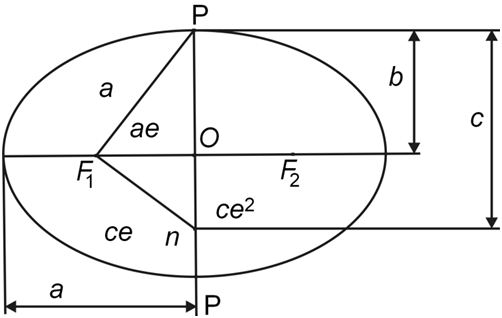
В воздушной навигации в большинстве случаях сжатием Земли пренебрегают и принимают Землю условно за шар, радиус которого составляет 6371 км.

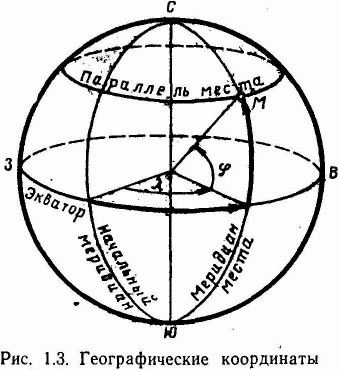
2. Основные географические точки, линии и круги на земном шаре.

Большим кругом называется окружность, образующаяся в результате сечения сферы плоскостью, проходящей через центр Земли.

Экватором называется большой круг, плоскость которого перпендикулярна оси вращения Земли

Меридианом истинным, или географическим, называется большой круг, плоскость которого проходит через ось вращения Земли.

На земном шаре можно провести бесчисленное количество меридианов. Все меридианы сходятся у географических полюсов земли и расходятся к экватору

Начальным меридианом, или нулевым, является Гринвичский меридиан, который когда-то проходил через расположенную вблизи г. Лондона Гринвичскую обсерваторию (сейчас обсерватория находится в другом месте, но меридиан сохранился).

Параллелью

---

называется малый круг, плоскость которого перпендикулярна оси вращения и параллельна экватору.

Широтой (φ) (географической широтой) называется угол, заключенный между плоскостью экватора и направлением нормали к земной поверхности в данную точку.

Нормалью называется перпендикуляр к касательной плоскости в данной точке эллипсоида.

Долготой (λ) (географической долготой) называется двугранный угол, заключенный между плоскостями начального меридиана и меридиана.

Широта отсчитывается от плоскости экватора к полюсам от 0 до 90° к северу или югу.

Долгота отсчитывается в обе стороны от начального меридиана от 0 до 180°. Если данная точка расположена в восточном полушарии, то долгота считается восточной, если в западном полушарии – западной.

При расчетах по формулам западной и восточной долготе можно приписывать знаки соответственно «–» и «+» (или наоборот, как это принято, например, в США).

Единицами измерения широты и долготы являются угловые градусы, минуты и секунды, а иногда и их десятичные доли (десятые, сотые и т. д.).

За рубежом используются следующие буквенные обозначения: N (North) – север; S (South) – юг; Е (East) – восток; W (West) – запад.

---

3. Системы координат, применяемые в воздушной навигации

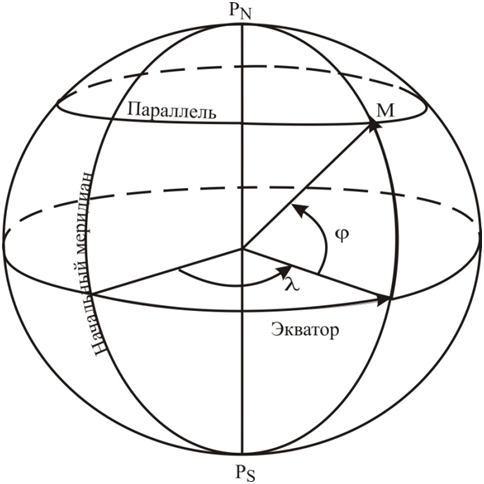
1. Географические координаты

Географические координаты — это угловые величины, которые определяют положение данной точки на земной поверхности. Гео­графическими координатами являются широта и долгота места (рис. 1.3).

Широтой места φ называется угол между плоскостью эк­ватора и направлением на дан­ную точку М из центра Земли или длина дуги меридиана, выра­женная в градусах, между эква­тором и параллелью данной точ­ки. Отсчет ведется от экватора к полюсам от 0 до 90°.

Долготой места λ назы­вается двугранный угол между плоскостью начального меридиана и плоскостью меридиана данной точки М или длина дуги экватора, выраженная в градусах, между начальным меридианом и меридианом данной точки. Долгота из­меряется в градусах. Отсчет ведется от начального меридиана к востоку и западу от 0 до 180°.

Меридиан, имеющий долготу 180°, по международному согла­шению принят в качестве линии смены дат и начала междуна­родной разграфки карт.

Долгота места, кроме угловых величин, может измеряться в единицах времени (часах, минутах и секундах).



2. Прямоугольные системы координат

Прямоугольные системы координат − это обычные декартовы системы, имеющие три перпендикулярных оси (X, Y, Z). Они используются для описания положения точек в пространстве, на поверхности или внутри Земли.



Если начало прямоугольной системы координат (точка пересечения трех осей) расположено в центре масс Земли, то систему называют геоцентрической, а если в центре аппроксимирующего Землю эллипсоида - референцной.

Системы координат, начало которых находится на поверхности Земли, называют топоцентрическими . Топоцентрические системы используются для определения положения точек на небольшой территории, в пределах которой кривизной Земли можно пренебречь.

В геоцентрических системах координат ось OZ направлена по оси вращения Земли, а в референцных – по малой оси эллипсоида в сторону Северного полюса. Оси ОХ и ОY лежат в плоскости экватора перпендикулярно друг другу.

---

В зависимости от того, вращается ли система координат вместе с Землей, различают гринвичские и инерциальные системы.



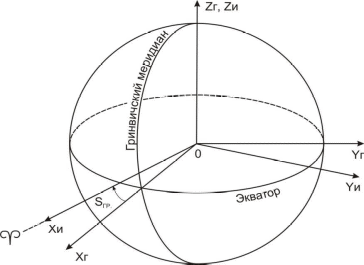
В гринвичскойсистеме координат ось ОХГ лежит в плоскости Гринвичского меридиана и пересекает поверхность Земли в точке с широтой и долготой равными нулю. Такая система координат вращается вместе с Землей, поэтому координаты точек на Земле в течение суток не меняются.

В инерциальнойсистеме координат ось ОХИ направлена в точку весеннего равноденствия на небесной сфере. Это точка, в которой пересекаются небесный экватор и эклиптика. Можно считать, что она занимает фиксированное положение относительно звезд. Поскольку эта система координат фиксирована относительно небесной сферы и вместе с Землей не вращается, координаты точек на вращающейся Земле непрерывно изменяются. Вместе с тем взаимное расположение инерциальной и гринвичской систем может быть точно определено в любой момент времени, поскольку угол между осями OXГ и ОХИ – это гринвичское звездное время (Sгр).

Сферические системы координат

Если Землю представить в виде сферы, то на ней может быть задана сферическая система координат.

Если полюсы сферической системы координат, то есть точки, в которых сходятся меридианы, совпадают с географическими полюсами Земли, то есть точками пересечения оси вращения Земли с ее поверхностью, то такую систему координат называют нормальной сферической.

Координатные линии на сфере задаются с помощью больших кругов.

Большим кругом на любой сфере называется линия, образованная путем сечения сферы плоскостью, проходящей через центр сферы.

Дуга большого круга на земной сфере в навигации называется ортодромией(по-английски – Great Circle) соединяет любые две точки, через которые она проходит, по кратчайшему расстоянию.

Остальные окружности на сфере, плоскости которых не проходят через ее центр, называются малыми кругами

---