КГЭУ	МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ЭНЕРГЕТИЧЕСКИЙ УНИВЕРСИТЕТ» (ФГБОУ ВО «КГЭУ»)

Кафедра АТПП


Реферат

по дисциплине «Адаптивные и оптимальные цифровые системы управления»

по теме: «Прохождение случайной функции через стационарную линейную систему»

Выполнил:

студент гр. ЗАТу-1-20

Габидуллин И.Р.

Преподаватель:
к.т.н., доцент каф. АТПП,
Борисова О.В.

Казань 2023

СОДЕРЖАНИЕ

Стр


ВВЕДЕНИЕ________________________________________________________ 3

СЛУЧАЙНЫЕ ПРОЦЕССЫ_________________________________________5

СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ__________ ___________ 11

ПРОХОЖДЕНИЕ СЛУЧАЙНОГО СИГНАЛА ЧЕРЕЗ ЛИНЕЙНУЮ СИСТЕМУ_______________________________________________________ 14

ЗАКЛЮЧЕНИЕ___________________________________________________24

ЛИТЕРАТУРА____________________________________________________26
ВВЕДЕНИЕ

Прежде чем рассматривать поведение автоматических систем при случайных воздействиях, напомним некоторые сведения о случайных величинах, случайных процессах и об их вероятностных характеристиках.

К категории случайных событий можно отнести такие, точное предсказание протекания которых в каждом отдельном случае оказывается невозможным.

Так, например, если бросать монету, то выпадение герба или цифры будет случайным событием. Если повторить этот эксперимент N раз, то можно зафиксировать определенное число выпадений герба  и число выпадений цифры  Относительная величина называется частотой события выпадения герба, а величина  — частотой события выпадения цифры.

Если устремить число экспериментов до бесконечности, то частоты событий будут стремиться к некоторому пределу

---

называемому вероятностью данного события. В рассмотренном случае очевидно, что обе вероятности выпадения герба и цифры одинаковы и равны 0,5.

Вероятность каждого события лежит в интервале 



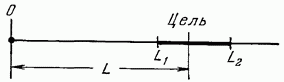
Рис. 11.1.

Если событие является невозможным, вероятность его равна нулю; если событие является достоверным, его вероятность равна единице.

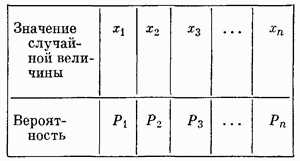
В примере с бросанием монеты рассматривалась дискретная случайная величина, которая могла принимать два фиксированных значения — выпадение герба и выпадение цифры. Существуют случайные величины, которые могут принимать непрерывные значения. Так, например, если рассмотреть стрельбу из орудия (рис. 11.1), то расстояние  от орудия до места падения снаряда будет случайной величиной, которая на определенном отрезке может принимать все возможные значения. В этом случае можно говорить о вероятности нахождения случайной величины  в некотором интервале от и до  Таблица 11.1



СЛУЧАЙНЫЕ ПРОЦЕССЫ

Случайная величина х, изменяющаяся во времени t, называется случайным или стохастическим процессом. Случайный процесс не есть определенная кривая х (t), а является множеством возможных кривых х (t), так же как случайная величина не имеет определенного значения, а является совокупностью (множеством) возможных значений.

Можно еще сказать, что случайный процесс есть такая функция времени, значение которой в каждый момент времени является случайной величиной.

Примерами случайных процессов могут, например, являться: координаты самолета, замеряемые радиолокационной станцией; угол визирования движущейся цели головкой самонаведения; помехи в системе телеуправления; нагрузка электрической сети и т. п.

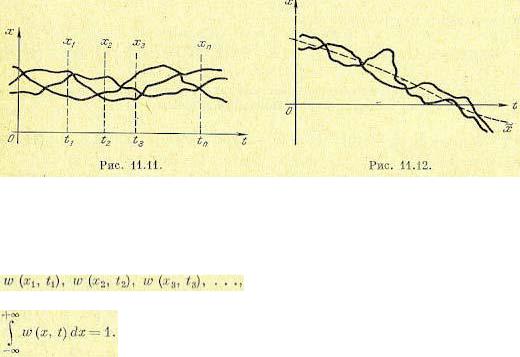
Итак, в случайном процессе нет определенной зависимости х (t). Каждая кривая множества (рис. 11.11) является лишь отдельной реализацией случайного процесса. Никогда нельзя сказать заранее, по какой кривой пойдет процесс.

Однако случайный процесс может быть оценен некоторыми вероятностными характеристиками.

В каждый отдельный момент времени

---

наблюдаются случайные величины  , каждая из которых имеет



свой закон распределения. Поскольку это — непрерывная случайная чина, то надо пользоваться понятием плотности вероятности.

Обозначим   закон распределения для всех этих отдельных случайных величин. В общем случае он меняется с течением времени. Для каждого данного t в отдельности

 будет свой закон распределения:

причем по свойству (11.14) для каждого из них

Для каждого заданного момента времени можно найти характеристики случайных величин, определенные в § 11.1. В результате будем иметь среднее по множеству (математическое ожидание)

(11.36)

и дисперсию

 (11,37)

Среднее значение случайного процесса представляет собой некоторую среднюю кривую (рис. 11.12), около которой группируются все возможные отдельные реализации этого процесса, а дисперсия D(t) или среднеквадратичное отклонение σ(t) характеризуют рассеяние отдельных возможных реализаций процесса около этой средней кривой.

Кроме этих осредненных характеристик  , которые для каждого данного момента времени являются средними по множеству, введем понятие среднего значения случайной

величины   для отдельной реализации случайного процесса х (t), которое определяется из выражения

 (11.38)

Переход к пределу здесь необходим для того, чтобы характеризовать не какой-нибудь отдельный участок кривой

---

, а всю возможную кривую х (t) в целом.

Для того чтобы знать связь между возможными значениями случайной функции х (г) ъ последующие моменты времени со значениями в предыдущие моменты, вводится понятие двумерной плотности вероятности

,

смысл которого можно пояснить следующим образом. Вероятность того, что в момент времени t1 величина х находится в интервале  , а в момент времени t2 — в интервале  , будет  . Это есть вероятность того, что кривая х (t) пройдет вблизи двух заданных точек  . Вводится также и тг-мерная плотность вероятности

.

Если ее умножить на	, то это будет вероятность того, что кривая пройдет
вблизи заданных п точек.
Случайный процесс полностью определяется видом функций		и связью

между ними.

Простейшим типом случайного процесса является чисто случайный процесс. В таком процессе все значения случайной величины в отдельные моменты времени   не зависят друг от друга. Тогда появления значений   и т.д. будут независимыми случайными событиями, для которых вероятность их совместного наступления равна, как известно, произведению вероятностей наступления каждого из них в отдельности. Следовательно, для чисто случайного процесса

---

 (11.39)

и вообще

 (11.40)

Это — самые простые соотношения в теории случайных процессов. Они могут применяться для характеристики некоторых видов помех (чисто случайные хаотические помехи).

Для характеристики полезных входных сигналов систем регулирования и следящих систем соотношения (11.39) и (11.40) практически не могут применяться, так как для этих сигналов ход процесса в последующие моменты времени в какой-то степени зависит от того, что было в предыдущие моменты времени.

Так, например, если речь идет о слежении за самолетом, то он не может как угодно быстро менять свое положение и скорость. Поэтому если он в момент времени t1 занял положение х1, то этим самым его возможное положение х2 в следующий момент t2 ограничено, т. е. события   не будут независимыми. Чем более инерционен изучаемый объект, тем больше эта взаимозависимость, или корреляция. В таких случаях вместо формулы (11.39) необходимо записать

 (11.41)

 — условная вероятность того, что случайный процесс пройдет вблизи точки

, если он уже прошел через точку  . Следовательно, зная плотности вероятности ю

, можно найти также и условную плотность вероятности

 (11.42)

Кроме того, имеет место следующая связь между основными плотностями вероятности:

 (11 43)

так как 

---

Смотрите также файлы

• Вопросы к экзамену по истории для студентов.doc

• Задача Перерисуйте таблицу. Цена (руб.) Qs1 Qs2 1 10 2 2 12 5 3 14 8 4 16 11 5 18 14.doc

• Итоговая работа.doc

• Отчет по практике учебная практика (указать вид практики) пм. 01 Обработка отраслевой информации.docx

• 1. Общее понятие договора, общий порядок заключения договора, структура договора (существенные и несущественные условия).docx