Файл: Реферат по дисциплине Адаптивные и оптимальные цифровые системы управления по теме Прохождение случайной функции через стационарную линейную систему.docx
Добавлен: 29.04.2024
Просмотров: 19
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
есть плотность вероятности случайной величины 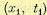 безотносительно к тому, какое потом будет значение
безотносительно к тому, какое потом будет значение 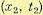 , т. е. допускается
, т. е. допускается 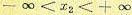 . Аналогичным образом любая плотность вероятности низшего порядка всегда может быть получена из высшей, т. е. высшие плотности вероятностей содержат наибольшее количество информации о случайном процессе (о взаимосвязях между возможными значениями случайной величины х в различные моменты времени).
. Аналогичным образом любая плотность вероятности низшего порядка всегда может быть получена из высшей, т. е. высшие плотности вероятностей содержат наибольшее количество информации о случайном процессе (о взаимосвязях между возможными значениями случайной величины х в различные моменты времени).
Написанные соотношения справедливы для случайных процессов любых типов. В зависимости же от того, до какого порядка принимаются во внимание плотности вероятности, а
также от разных дополнительных гипотез о формах связи между рассматриваются разные типы случайных процессов в отличие от чисто случайных.
рассматриваются разные типы случайных процессов в отличие от чисто случайных.
Другая классификация всех случайных процессов состоит в разделении их на стационарные и нестационарные. Теория стационарных случайных процессов наиболее разработана и чаще всего применяется на практике.
СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Стационарным случайным процессом называется такой процесс, вероятностные характеристики которого не зависят от времени. Все плотности вероятностей не меняются при любом сдвиге рассматриваемого участка процесса во времени, т. е. при сохранении постоянной разности.
не меняются при любом сдвиге рассматриваемого участка процесса во времени, т. е. при сохранении постоянной разности.
Можно сказать, что стационарный случайный процесс в какой-то мере аналогичен обычным стационарным или установившимся процессам в автоматических системах. Например, при рассмотрении обычных установившихся периодических колебаний ничего не изменится, если перенести начало отсчета на какую-нибудь величину. При этом сохранят свои значения такие характеристики, как частота, амплитуда, среднеквадратичное значение и т. п. В стационарном случайном процессе закон распределения один и тот же для каждого момента времени, т. е. плотность вероятности не зависит от времени:
 .
.
Отсюда получаем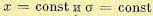 вдоль всего случайного процесса. Следовательно, в стационарном случайном процессе средняя линия, в отличие от общего случая (см. рис. 11.12),
вдоль всего случайного процесса. Следовательно, в стационарном случайном процессе средняя линия, в отличие от общего случая (см. рис. 11.12),
будет прямая , подобно постоянному смещению средней линии обычных периодических колебаний. Рассеяние значений переменной х в стационарном случайном
, подобно постоянному смещению средней линии обычных периодических колебаний. Рассеяние значений переменной х в стационарном случайном
.процессе, определяемое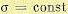 , также будет все время одинаковым, подобно постоянному значению среднеквадратичного отклонения обычных установившихся колебаний от средней линии.
, также будет все время одинаковым, подобно постоянному значению среднеквадратичного отклонения обычных установившихся колебаний от средней линии.
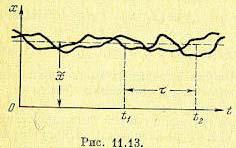
Аналогичным образом и двумерная плотность вероятности также будет «одна и та же для одного и того же промежутка времени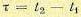 между любыми t1 и t2 (рис. 11.13), т. е.
между любыми t1 и t2 (рис. 11.13), т. е.
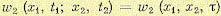 (11.44)
(11.44)
и также для n-мерной плотности вероятности.
Задание всех этих функций распределения плотности определяет случайный процесс. Однако более удобно иметь дело с некоторыми осреднен-ными и характеристиками процесса.
Прежде чем перейти к ним, отметим два важных для практики ^свойства.
1.Ограничиваясь только стационарными случайными процессами, можно будет определить только установившиеся (стационарные) динамиче--ские ошибки автоматических систем при случайных воздействиях. Такой прием применялся и ранее при рассмотрении регулярных воздействий, когда определялись динамические свойства систем регулирования по величине динамических ошибок в установившемся периодическом режиме.
2.Стационарные случайные процессы обладают замечательным свойством, которое известно под названием эргодической гипотезы.
Для стационарного случайного процесса с вероятностью, равной единице (т. е. практически достоверно), всякое среднее по множеству равно соответствующему среднему по времени, в
частности
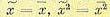 и т. д.
и т. д.
В самом деле, поскольку вероятностные характеристики стационарного случайного
процесса с течением времени не меняются (например,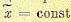 ), то длительное наблюдение случайного процесса на одном объекте (среднее ло времени) дает в среднем такую же картину, как и большое число наблюдений, сделанное в один и тот же момент времени на большом числе одинаковых объектов (среднее по множеству).
), то длительное наблюдение случайного процесса на одном объекте (среднее ло времени) дает в среднем такую же картину, как и большое число наблюдений, сделанное в один и тот же момент времени на большом числе одинаковых объектов (среднее по множеству).
Для многих случаев существует математическое доказательство этого свойства. Тогда оно сводится к эргодической теореме.
Итак, среднее значение (математическое ожидание) для стационарного «процесса будет
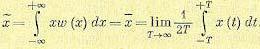 (11.45)
(11.45)
Аналогичным образом могут быть записаны моменты более высоких порядков — дисперсия, среднеквадратичное отклонение и т. п.
Эргодическая гипотеза позволяет сильно упрощать все расчеты и эксперименты. Она
позволяет для определения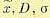 и т. п., вместо параллельного испытания многих однотипных систем в один и тот же момент времени, пользоваться одной кривой х (t), полученной при испытании одной системы в течение длительного времени.
и т. п., вместо параллельного испытания многих однотипных систем в один и тот же момент времени, пользоваться одной кривой х (t), полученной при испытании одной системы в течение длительного времени.
Таким образом, важное свойство стационарного случайного процесса •состоит в том, что отдельная его реализация на бесконечном промежутке времени полностью определяет собой весь случайный процесс со всеми бесчисленными возможными его реализациями. Этим свойством не обладает никакой другой тип случайного процесса.
ПРОХОЖДЕНИЕ СЛУЧАЙНОГО СИГНАЛА ЧЕРЕЗ ЛИНЕЙНУЮ СИСТЕМУ
Рассмотрим линейную систему (рис. 11.25) с передаточной функцией W(р) и функцией веса . Пусть на входе действует случайный сигнал
. Пусть на входе действует случайный сигнал 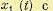 с корреляционной функцией
с корреляционной функцией
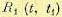 .
.
Выходной сигнал х2 (t) на основании формулы свертки (7.44)
Рассматривая в этой формуле математические ожидания, имеем
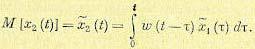 (11.95)
(11.95)
Для получения корреляционной функции на выходе запишем исходную формулу для центрированных значений для двух моментов времени:
для двух моментов времени:
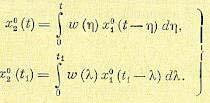 (11.96)
(11.96)
После перемножения получим
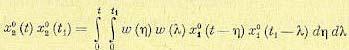 (11.97)
(11.97)
Далее, переходя к математическому ожиданию, можно найти корреляционную функцию
 (11.98)
(11.98)
Для определения дисперсии на выходе О2(1) в формуле (11.98) следует положить . Тогда
. Тогда
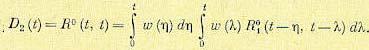 (11.99)
(11.99)
В случае использования канонического разложения случайной функции
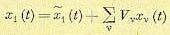 (11.100)
(11.100)
выходная величина может быть представлена в виде
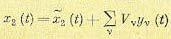 (11.101)
(11.101)

где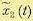 определяется формулой (11.95), а координатные функции
определяется формулой (11.95), а координатные функции
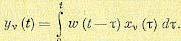 (11.102)
(11.102)
Корреляционная функция выходного сигнала
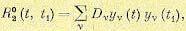 (11.103)
(11.103)
а дисперсия
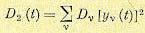 (11.104)
(11.104)
Для нахождения математического ожидания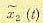 и координатных функций
и координатных функций 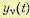
в соответствии с выражениями (11.95) и (11.102) могут использоваться различные методы построения переходных процессов (см. главу 7),
В случае, когда на входе (рис. 11.25) действует случайный стационарный процесс,
корреляционная функция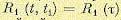 зависит только от сдвига
зависит только от сдвига 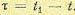 . Однако на выходе линейной системы процесс некоторое время после включения будет устанавливаться и не будет стационарным. Корреляционная функция на выходе может быть получена из общего выражения (11.98);
. Однако на выходе линейной системы процесс некоторое время после включения будет устанавливаться и не будет стационарным. Корреляционная функция на выходе может быть получена из общего выражения (11.98);
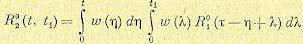 (11.105)
(11.105)
а дисперсия – из (11.99)
Если рассматриваемая система устойчива, то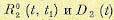 стремятся к некоторым пределам, которые определяют стационарный процесс на выходе. Они могут быть найдены из
стремятся к некоторым пределам, которые определяют стационарный процесс на выходе. Они могут быть найдены из
(11.105) и (11.1 06) , если положить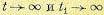 .
.
Тогда
Пусть, например, на входе интегрирующего звена с передаточной функцией и функцией веса
и функцией веса 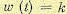 действует белый шум с корреляционной функцией
действует белый шум с корреляционной функцией
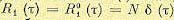 . Тогда в соответствии: с (11.106) дисперсия на выходе будет
. Тогда в соответствии: с (11.106) дисперсия на выходе будет
т. е. дисперсия растет пропорционально времени. Нетрудно видеть, что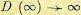 , так как звено не является устойчивым, а оно находится на границе устойчивости (нейтральноустойчиво).
, так как звено не является устойчивым, а оно находится на границе устойчивости (нейтральноустойчиво).
Для расчета установившегося стационарного процесса на выходе системы (рис. 11.25) более удобно исходить из известной спектральной плотности на входе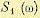
Написанные соотношения справедливы для случайных процессов любых типов. В зависимости же от того, до какого порядка принимаются во внимание плотности вероятности, а
также от разных дополнительных гипотез о формах связи между
Другая классификация всех случайных процессов состоит в разделении их на стационарные и нестационарные. Теория стационарных случайных процессов наиболее разработана и чаще всего применяется на практике.

СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Стационарным случайным процессом называется такой процесс, вероятностные характеристики которого не зависят от времени. Все плотности вероятностей
Можно сказать, что стационарный случайный процесс в какой-то мере аналогичен обычным стационарным или установившимся процессам в автоматических системах. Например, при рассмотрении обычных установившихся периодических колебаний ничего не изменится, если перенести начало отсчета на какую-нибудь величину. При этом сохранят свои значения такие характеристики, как частота, амплитуда, среднеквадратичное значение и т. п. В стационарном случайном процессе закон распределения один и тот же для каждого момента времени, т. е. плотность вероятности не зависит от времени:
Отсюда получаем
будет прямая
.процессе, определяемое
Аналогичным образом и двумерная плотность вероятности также будет «одна и та же для одного и того же промежутка времени
и также для n-мерной плотности вероятности.
Задание всех этих функций распределения плотности определяет случайный процесс. Однако более удобно иметь дело с некоторыми осреднен-ными и характеристиками процесса.
Прежде чем перейти к ним, отметим два важных для практики ^свойства.
1.Ограничиваясь только стационарными случайными процессами, можно будет определить только установившиеся (стационарные) динамиче--ские ошибки автоматических систем при случайных воздействиях. Такой прием применялся и ранее при рассмотрении регулярных воздействий, когда определялись динамические свойства систем регулирования по величине динамических ошибок в установившемся периодическом режиме.
2.Стационарные случайные процессы обладают замечательным свойством, которое известно под названием эргодической гипотезы.
Для стационарного случайного процесса с вероятностью, равной единице (т. е. практически достоверно), всякое среднее по множеству равно соответствующему среднему по времени, в
частности
В самом деле, поскольку вероятностные характеристики стационарного случайного
процесса с течением времени не меняются (например,
Для многих случаев существует математическое доказательство этого свойства. Тогда оно сводится к эргодической теореме.
Итак, среднее значение (математическое ожидание) для стационарного «процесса будет
Аналогичным образом могут быть записаны моменты более высоких порядков — дисперсия, среднеквадратичное отклонение и т. п.
Эргодическая гипотеза позволяет сильно упрощать все расчеты и эксперименты. Она
позволяет для определения
Таким образом, важное свойство стационарного случайного процесса •состоит в том, что отдельная его реализация на бесконечном промежутке времени полностью определяет собой весь случайный процесс со всеми бесчисленными возможными его реализациями. Этим свойством не обладает никакой другой тип случайного процесса.
ПРОХОЖДЕНИЕ СЛУЧАЙНОГО СИГНАЛА ЧЕРЕЗ ЛИНЕЙНУЮ СИСТЕМУ
Рассмотрим линейную систему (рис. 11.25) с передаточной функцией W(р) и функцией веса
Выходной сигнал х2 (t) на основании формулы свертки (7.44)
Рассматривая в этой формуле математические ожидания, имеем
Для получения корреляционной функции на выходе запишем исходную формулу для центрированных значений
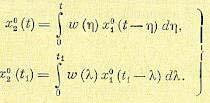 (11.96)
(11.96)После перемножения получим
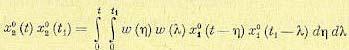 (11.97)
(11.97)Далее, переходя к математическому ожиданию, можно найти корреляционную функцию
Для определения дисперсии на выходе О2(1) в формуле (11.98) следует положить
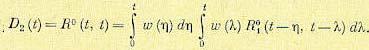 (11.99)
(11.99)В случае использования канонического разложения случайной функции
выходная величина может быть представлена в виде

где
Корреляционная функция выходного сигнала
а дисперсия
Для нахождения математического ожидания
в соответствии с выражениями (11.95) и (11.102) могут использоваться различные методы построения переходных процессов (см. главу 7),
В случае, когда на входе (рис. 11.25) действует случайный стационарный процесс,
корреляционная функция
а дисперсия – из (11.99)
Если рассматриваемая система устойчива, то
(11.105) и (11.1 06) , если положить
Тогда
Пусть, например, на входе интегрирующего звена с передаточной функцией
т. е. дисперсия растет пропорционально времени. Нетрудно видеть, что
Для расчета установившегося стационарного процесса на выходе системы (рис. 11.25) более удобно исходить из известной спектральной плотности на входе


