Файл: Ответы к экзаменационным вопросам по предмету Основы энергетики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.05.2024
Просмотров: 56
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
0р-и = DН0гор = - 1656,8 кДж/моль или Qгор = + 2656,8 кДж/моль.
Таким образом, при сгорании 1 моля бутана выделяется 2656,8 кДж тепла.
В пожарно-технических расчетах часто пользуются понятием удельной теплоты горения. Удельная теплота горения – это количество теплоты, которое выделяется при полном сгорании единицы массы или объема горючего вещества. Размерность удельной теплоты горения – кДж/кг или кДж/м3.
В зависимости от агрегатного состояния воды в продуктах горения различают низшую и высшую теплоту горения. Если вода находится в парообразном состоянии, то теплоту горения называют низшей теплотой горения Qн. Если пары воды конденсируются в жидкость, то теплота горения – высшая Qв.
Температура пламени достигает 100 К и выше, а вода кипит при 373 К, поэтому в продуктах горения на пожаре вода всегда находится в парообразном состоянии, и для расчетов в пожарном деле используется низшая теплота горения Qн.
Низшая теплота горения индивидуальных веществ может быть определена переводом значения DНгор, кДж/моль в Qн, кДж/кг или кДж/м3. Для веществ сложного элементного состава низшая теплота горения может быть определена по формуле Д.И. Менделеева. Кроме того, для многих веществ значения низшей теплоты горения приведены в справочной литературе [ ], некоторые данные представлены в приложении 2.
Значение DНгор = - 2256,3 кДж/моль показывает, что при сгорании 1 моля этилацетата выделяется 2256,3 кДж тепла, т.е. Qгор= + 2256,3 кДж/моль.
1 моль СН3СООС2Н5 имеет массу 88 г. Можно составить пропорцию
М (СН3СООС2Н5) = 88 г/моль ¾ Qгор= 2256,3 кДж/моль
1 кг = 1000 г ¾ Qн кДж/кг
 кДж/кг
кДж/кг
В общем виде формула для перевода из размерности кДж/моль в кДж/кг выглядит следующим образом:

; кДж/кг (2)
Если необходимо осуществить перевод из размерности кДж/моль в кДж/м3, то можно воспользоваться формулой
 , кДж/м3. (3)
, кДж/м3. (3)
Значения низшей теплоты сгорания веществ и материалов могут быть рассчитаны по формуле Д.И.Менделеева. Данная формула может быть использована для расчетов Qн веществ сложного элементного состава, а также для любых индивидуальных веществ, если предварительно рассчитать массовую долю каждого элемента в соединении (w).
QН = 339,4×w(C) + 1257×w(H) - 108,9 [(w(O) +w(N)) -w(S)] - 25,1[9×w(H) +w(W)], кДж/кг,
(4)
где
w (С), w (Н), w (S), w (О),w (N) – – массовые доли элементов в веществе, %; w (W) – содержание влаги в веществе, %.
1. Для того, чтобы воспользоваться данной формулой, необходим расчет процентного состава каждого элемента в веществе (массовой доли).
Молярная масса сульфадимезина С12Н14О2N4S составляет 278 г/моль.
w(C) = (12×12)/278 = 144/278 = 0,518 ×100 = 51,8 %
w(H) = (1×14)/278 = 14/278 = 0,05 ×100 = 5,0 %
w(O) = (16×2)/278 = 32/278 = 0,115 ×100 = 11,5 %
w(N) = (14×4)/278 = 56/278 = 0,202 ×100 = 20,2 %
w(S) = 100 – (51,8 + 5,0 + 11,5 + 20,2) = 11,5 %
2. Подставляем найденные значения в формулу Д.И. Менделеева.
QН = 339,4×51,8+1257×5,0-108,9×(11,5+20,2-11,5)-25,1×9×5,0 = 22741 кДж/кг.
Теплота горения смеси газов и паров определяется как сумма произведений теплот горения каждого горючего компонента (Qн = Qгор) на его объемную долю в смеси (jоб):
Qн= , кДж/м3. (5)
, кДж/м3. (5)
Можно воспользоваться эмпирической формулой для расчета Qн для газовой смеси:
Qн = 126,5×j(СО) + 107,7×j(Н2) + 358,2×j(СН4) + 590,8×j(С2Н4) + 636,9×j(С2Н6) +
+ 913,4×j(С3Н8) + 1185,8×j(С4Н10) + 1462,3×j(С5Н12) + 234,6×j(Н2S), кДж/м3 (6)
5. Теория теплообмена
Теория теплопередачи рассматривает процессы передачи тепла из одной части пространства в другую.
Процесс теплообмена наблюдается тогда, когда тепло передается от одного, более нагретого тела, к другому, менее нагретому. Поток энергии, передаваемый частицами более нагретого тела частицам менее нагретого, называется тепловым потоком. Таким образом, для того чтобы происходил процесс передачи тепла от одного тела к другому, совершенно необходима разность температур тел, участвующих в теплообмене. Следовательно, тепловой поток всегда направлен в сторону меньших температур и, являясь величиной векторной, характеризуется не только абсолютной величиной, но и направлением.
Температура, являясь величиной скалярной, не зависит от направления и характеризуется лишь абсолютной величиной. Температура характеризует степень нагретости тела и измеряется в градусах стоградусной или абсолютной температурной шкалы.
Процесс передачи тепла развивается как во времени, так и в пространстве. Практически часто бывает необходимо знать температуру в различных точках изучаемого пространства в один и тот же момент времени. Подобное распределение температур называется полем температур или температурным полем.
Кроме изменения в пространстве, температурное поле и поле тепловых потоков может изменяться также и во времени. Таким образом, в общем случае температура Т может являться функцией координат х, у, г и времени т, т. е. Т=f(х, у, г, т).
Если температура (тепловой поток) с течением времени не претерпевает никаких изменении, то говорят о «стационарном тепловом состоянии». Если же температура изменяется со временем, то такой процесс называется нестационарным.
Различают полный и удельный тепловые потоки. Полный тепловой поток Q обычно относится к единице времени и измеряется в ваттах (Вт). Тепловой поток, отнесенный к единице поверхности, называется плотностью теплового потока q (Вт/м2).
Таким образом, если F теплопередающая поверхность (м2), то
Q = q F. (25)
Иногда Q обозначает полное количество переданного тепла и выражается в джоулях (Дж) и тогда Q =qτF. (26)
где τ — время, с.
Различают три основных вида передачи тепла: конвекцию, теплопроводность, тепловое излучение.
Конвективным теплообменом называют такой процесс, когда движущаяся жидкость или газ переносит тепло из более нагретых областей в менее нагретые. В технике чаще всего рассматривают конвективный теплообмен жидкости или газа с поверхностью твердых тел, при котором тепло транспортируется к поверхности (или от нее) движущимися объемами жидкости или газа. Если нет движения жидкости (газа), то нет и передачи тепла конвекцией.
Теплопроводность — передача тепла от одних частей тела к другим без заметного перемещения частиц. Передача тепла теплопроводностью наиболее характерно осуществляется в гомогенных непрозрачных твердых телах. В металлургической практике процессы передачи тепла теплопроводностью лежат в основе теории и практики нагрева металла. Передача тепла теплопроводностью возможна как при стационарном состоянии, так и при нестационарном. При стационарном состоянии передача тепла от одной точки пространства к другой происходит без изменения их температуры во времени.
При нестационарном состоянии происходит изменение температуры тела во времени, т. е. тело или нагревается, или остывает. При этом его энтальпия или растет, или убывает, причем тело тем быстрее нагревается, чем выше его теплопроводность. Однако на интенсивность изменения энтальпии тела наряду с теплопроводностью тела оказывает влияние и величина теплоемкости тела. Но влияние это обратное. Чем выше теплоемкость тела, тем медленнее оно изменяет энтальпию и температуру. Таким образом, энтальпия тела изменяется тем быстрее, чем выше способность материала проводить тепло, т. е. чем больше коэффициент теплопроводности λ. Вместе с тем скорость изменения энтальпии тела обратно пропорциональна его аккумулирующей способности, которая определяется массовой теплоемкостью ρс. Таким образом, в общем, скорость изменения энтальпии тела определяется соотношением величин λ и ρс, совместное влияние которых на нагрев или охлаждение тела выражается изменением коэффициента температуропроводности а = λ /(ρс) м2/с, имеющим важное значение для нестационарных процессов передачи тепла теплопроводностью.
Природа теплового излучения принципиально отличается от передачи тепла конвекцией и теплопроводностью, при которых переход тепла связан с передачей энергии молекулами, образующими твердую, жидкую или газообразную среду. При тепловом излучении энергия передается электромагнитными волнами определенной длины (инфракрасные лучи). Тепловое излучение возможно даже в вакууме; оно не зависит от температуры окружающей среды.
Чтобы решить дифференциальные уравнения для конкретного случая, необходимо, кроме основного дифференциального уравнения, сформулировать дополнительные условия, характерные только для этого случая, которые называют краевыми условиями.
Начальные краевые условия показывают температурное состояние тела перед тем, как начался процесс нагрева. Это
температурное состояние может быть различным, но оно обязательно должно быть задано в виде уравнения (в общем виде), дающего распределение температуры в теле по трем осям координат, т.е. при τ = 0 и Тнач=f(х, у, г).
Наиболее простые и часто встречающиеся на практике временные условия показывают, что температура во всех точках тела в начальный момент времени одинакова, т. е. при τ = 0 Тнач=const.
В 1807 году французский ученый Фурье доказал экспериментально, что во всякой точке тела (вещества) в процессе теплопроводности присуща однозначная взаимосвязь между тепловым потоком и градиентом температуры:
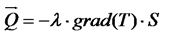 ,
,
где Q – тепловой поток, выражается в Вт;
grad(T) – градиент температурного поля (совокупности числовых значений температуры в разнообразных местах системы в выбранный момент времени), единицы измерения К/м;
S – площадь поверхности теплообмена, м2;
λ – коэффициент теплопроводности, Вт/(м К).
Градиент температуры получится характеризовать в виде векторной суммы составляющих по осям декартовых координат:
 ,
,
где i, j, k – ортогональные между собой единичные векторы, нацеленные по координатным осям.
Значит, данный закон устанавливает величину теплового потока при переносе тепла посредством теплопроводности.
Закон Фурье для поверхностной плотности теплового потока принимает вид:
 .
.
Знак «минус» обозначает, что векторы теплового потока и градиента температуры разнонаправленные. Следует понимать, что теплота передается в направлении спада температуры.
И все же не лишним будет указать, что закон Фурье не принимает в расчет инерционность процесса теплопроводности, иначе говоря, в представленной модели колебание температуры в любой точке мгновенно распространяется на всё тело. Закон Фурье некорректно применять для характеристики
Таким образом, при сгорании 1 моля бутана выделяется 2656,8 кДж тепла.
В пожарно-технических расчетах часто пользуются понятием удельной теплоты горения. Удельная теплота горения – это количество теплоты, которое выделяется при полном сгорании единицы массы или объема горючего вещества. Размерность удельной теплоты горения – кДж/кг или кДж/м3.
В зависимости от агрегатного состояния воды в продуктах горения различают низшую и высшую теплоту горения. Если вода находится в парообразном состоянии, то теплоту горения называют низшей теплотой горения Qн. Если пары воды конденсируются в жидкость, то теплота горения – высшая Qв.
Температура пламени достигает 100 К и выше, а вода кипит при 373 К, поэтому в продуктах горения на пожаре вода всегда находится в парообразном состоянии, и для расчетов в пожарном деле используется низшая теплота горения Qн.
Низшая теплота горения индивидуальных веществ может быть определена переводом значения DНгор, кДж/моль в Qн, кДж/кг или кДж/м3. Для веществ сложного элементного состава низшая теплота горения может быть определена по формуле Д.И. Менделеева. Кроме того, для многих веществ значения низшей теплоты горения приведены в справочной литературе [ ], некоторые данные представлены в приложении 2.
| Перевод значения энтальпии горения из кДж/моль в кДж/кг | Пример 2. Энтальпия горения этилацетата СН3СООС2Н5 равна DНгор = - 2256,3 кДж/моль. Выразить эту величину в кДж/кг. |
Значение DНгор = - 2256,3 кДж/моль показывает, что при сгорании 1 моля этилацетата выделяется 2256,3 кДж тепла, т.е. Qгор= + 2256,3 кДж/моль.
1 моль СН3СООС2Н5 имеет массу 88 г. Можно составить пропорцию
М (СН3СООС2Н5) = 88 г/моль ¾ Qгор= 2256,3 кДж/моль
1 кг = 1000 г ¾ Qн кДж/кг
В общем виде формула для перевода из размерности кДж/моль в кДж/кг выглядит следующим образом:

; кДж/кг (2)
Если необходимо осуществить перевод из размерности кДж/моль в кДж/м3, то можно воспользоваться формулой
 , кДж/м3. (3)
, кДж/м3. (3)| Расчет низшей теплоты сгорания Qн по формуле Д.И. Менделеева | Пример 3. Вычислить низшую теплоту сгорания сульфадимезина С12Н14О2N4S по формуле Д.И. Менделеева. |
Значения низшей теплоты сгорания веществ и материалов могут быть рассчитаны по формуле Д.И.Менделеева. Данная формула может быть использована для расчетов Qн веществ сложного элементного состава, а также для любых индивидуальных веществ, если предварительно рассчитать массовую долю каждого элемента в соединении (w).
QН = 339,4×w(C) + 1257×w(H) - 108,9 [(w(O) +w(N)) -w(S)] - 25,1[9×w(H) +w(W)], кДж/кг,
(4)
где
w (С), w (Н), w (S), w (О),w (N) – – массовые доли элементов в веществе, %; w (W) – содержание влаги в веществе, %.
1. Для того, чтобы воспользоваться данной формулой, необходим расчет процентного состава каждого элемента в веществе (массовой доли).
Молярная масса сульфадимезина С12Н14О2N4S составляет 278 г/моль.
w(C) = (12×12)/278 = 144/278 = 0,518 ×100 = 51,8 %
w(H) = (1×14)/278 = 14/278 = 0,05 ×100 = 5,0 %
w(O) = (16×2)/278 = 32/278 = 0,115 ×100 = 11,5 %
w(N) = (14×4)/278 = 56/278 = 0,202 ×100 = 20,2 %
w(S) = 100 – (51,8 + 5,0 + 11,5 + 20,2) = 11,5 %
2. Подставляем найденные значения в формулу Д.И. Менделеева.
QН = 339,4×51,8+1257×5,0-108,9×(11,5+20,2-11,5)-25,1×9×5,0 = 22741 кДж/кг.
Теплота горения смеси газов и паров определяется как сумма произведений теплот горения каждого горючего компонента (Qн = Qгор) на его объемную долю в смеси (jоб):
Qн=
Можно воспользоваться эмпирической формулой для расчета Qн для газовой смеси:
Qн = 126,5×j(СО) + 107,7×j(Н2) + 358,2×j(СН4) + 590,8×j(С2Н4) + 636,9×j(С2Н6) +
+ 913,4×j(С3Н8) + 1185,8×j(С4Н10) + 1462,3×j(С5Н12) + 234,6×j(Н2S), кДж/м3 (6)
5. Теория теплообмена
Теория теплопередачи рассматривает процессы передачи тепла из одной части пространства в другую.
Процесс теплообмена наблюдается тогда, когда тепло передается от одного, более нагретого тела, к другому, менее нагретому. Поток энергии, передаваемый частицами более нагретого тела частицам менее нагретого, называется тепловым потоком. Таким образом, для того чтобы происходил процесс передачи тепла от одного тела к другому, совершенно необходима разность температур тел, участвующих в теплообмене. Следовательно, тепловой поток всегда направлен в сторону меньших температур и, являясь величиной векторной, характеризуется не только абсолютной величиной, но и направлением.
Температура, являясь величиной скалярной, не зависит от направления и характеризуется лишь абсолютной величиной. Температура характеризует степень нагретости тела и измеряется в градусах стоградусной или абсолютной температурной шкалы.
Процесс передачи тепла развивается как во времени, так и в пространстве. Практически часто бывает необходимо знать температуру в различных точках изучаемого пространства в один и тот же момент времени. Подобное распределение температур называется полем температур или температурным полем.
Кроме изменения в пространстве, температурное поле и поле тепловых потоков может изменяться также и во времени. Таким образом, в общем случае температура Т может являться функцией координат х, у, г и времени т, т. е. Т=f(х, у, г, т).
Если температура (тепловой поток) с течением времени не претерпевает никаких изменении, то говорят о «стационарном тепловом состоянии». Если же температура изменяется со временем, то такой процесс называется нестационарным.
Различают полный и удельный тепловые потоки. Полный тепловой поток Q обычно относится к единице времени и измеряется в ваттах (Вт). Тепловой поток, отнесенный к единице поверхности, называется плотностью теплового потока q (Вт/м2).
Таким образом, если F теплопередающая поверхность (м2), то
Q = q F. (25)
Иногда Q обозначает полное количество переданного тепла и выражается в джоулях (Дж) и тогда Q =qτF. (26)
где τ — время, с.
Различают три основных вида передачи тепла: конвекцию, теплопроводность, тепловое излучение.
Конвективным теплообменом называют такой процесс, когда движущаяся жидкость или газ переносит тепло из более нагретых областей в менее нагретые. В технике чаще всего рассматривают конвективный теплообмен жидкости или газа с поверхностью твердых тел, при котором тепло транспортируется к поверхности (или от нее) движущимися объемами жидкости или газа. Если нет движения жидкости (газа), то нет и передачи тепла конвекцией.
Теплопроводность — передача тепла от одних частей тела к другим без заметного перемещения частиц. Передача тепла теплопроводностью наиболее характерно осуществляется в гомогенных непрозрачных твердых телах. В металлургической практике процессы передачи тепла теплопроводностью лежат в основе теории и практики нагрева металла. Передача тепла теплопроводностью возможна как при стационарном состоянии, так и при нестационарном. При стационарном состоянии передача тепла от одной точки пространства к другой происходит без изменения их температуры во времени.
При нестационарном состоянии происходит изменение температуры тела во времени, т. е. тело или нагревается, или остывает. При этом его энтальпия или растет, или убывает, причем тело тем быстрее нагревается, чем выше его теплопроводность. Однако на интенсивность изменения энтальпии тела наряду с теплопроводностью тела оказывает влияние и величина теплоемкости тела. Но влияние это обратное. Чем выше теплоемкость тела, тем медленнее оно изменяет энтальпию и температуру. Таким образом, энтальпия тела изменяется тем быстрее, чем выше способность материала проводить тепло, т. е. чем больше коэффициент теплопроводности λ. Вместе с тем скорость изменения энтальпии тела обратно пропорциональна его аккумулирующей способности, которая определяется массовой теплоемкостью ρс. Таким образом, в общем, скорость изменения энтальпии тела определяется соотношением величин λ и ρс, совместное влияние которых на нагрев или охлаждение тела выражается изменением коэффициента температуропроводности а = λ /(ρс) м2/с, имеющим важное значение для нестационарных процессов передачи тепла теплопроводностью.
Природа теплового излучения принципиально отличается от передачи тепла конвекцией и теплопроводностью, при которых переход тепла связан с передачей энергии молекулами, образующими твердую, жидкую или газообразную среду. При тепловом излучении энергия передается электромагнитными волнами определенной длины (инфракрасные лучи). Тепловое излучение возможно даже в вакууме; оно не зависит от температуры окружающей среды.
Чтобы решить дифференциальные уравнения для конкретного случая, необходимо, кроме основного дифференциального уравнения, сформулировать дополнительные условия, характерные только для этого случая, которые называют краевыми условиями.
Начальные краевые условия показывают температурное состояние тела перед тем, как начался процесс нагрева. Это
температурное состояние может быть различным, но оно обязательно должно быть задано в виде уравнения (в общем виде), дающего распределение температуры в теле по трем осям координат, т.е. при τ = 0 и Тнач=f(х, у, г).
Наиболее простые и часто встречающиеся на практике временные условия показывают, что температура во всех точках тела в начальный момент времени одинакова, т. е. при τ = 0 Тнач=const.
В 1807 году французский ученый Фурье доказал экспериментально, что во всякой точке тела (вещества) в процессе теплопроводности присуща однозначная взаимосвязь между тепловым потоком и градиентом температуры:
где Q – тепловой поток, выражается в Вт;
grad(T) – градиент температурного поля (совокупности числовых значений температуры в разнообразных местах системы в выбранный момент времени), единицы измерения К/м;
S – площадь поверхности теплообмена, м2;
λ – коэффициент теплопроводности, Вт/(м К).
Градиент температуры получится характеризовать в виде векторной суммы составляющих по осям декартовых координат:
 ,
,где i, j, k – ортогональные между собой единичные векторы, нацеленные по координатным осям.
Значит, данный закон устанавливает величину теплового потока при переносе тепла посредством теплопроводности.
Закон Фурье для поверхностной плотности теплового потока принимает вид:
Знак «минус» обозначает, что векторы теплового потока и градиента температуры разнонаправленные. Следует понимать, что теплота передается в направлении спада температуры.
И все же не лишним будет указать, что закон Фурье не принимает в расчет инерционность процесса теплопроводности, иначе говоря, в представленной модели колебание температуры в любой точке мгновенно распространяется на всё тело. Закон Фурье некорректно применять для характеристики

