Файл: Ответы к экзаменационным вопросам по предмету Основы энергетики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.05.2024
Просмотров: 69
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
краевыми условиями. Начальные условия при нагреве (или охлаждении) тела сказываются только в начальный период, но по истечении некоторого времени наступает регулярный режим, при котором распределение температур в теле определяется только граничными условиями и не зависит от начальных. Граничные условия задаются соответственно способу нагрева (охлаждения), т.е. воздействию окружающей среды на тело.
1.Если задается изменение температуры на поверхности тела во времени tпов= f(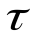 ), то это отвечает граничным условиямпервого рода. На практике встречаются случаи нагрева или охлаждения при заданном изменении температуры на поверхности, например, по прямолинейному закону tпов=t0 +b
), то это отвечает граничным условиямпервого рода. На практике встречаются случаи нагрева или охлаждения при заданном изменении температуры на поверхности, например, по прямолинейному закону tпов=t0 +b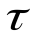 . При очень интенсивном теплообмене температура стенки близка к температуре среды, т.е.
. При очень интенсивном теплообмене температура стенки близка к температуре среды, т.е. 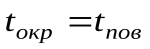 , и этот случай близок к условиям первого рода.
, и этот случай близок к условиям первого рода.
2.Если на поверхности тела задана плотность теплового потока, то мы имеем граничные условия второго рода. По закону Фурье
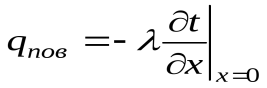 . (1.19)
. (1.19)
Градиент температуры относится к точке тела, расположенной в непосредственной близости от поверхности тела (х= +0).
3.Граничные условия третьего рода соответствуют случаю конвективного теплообмена с поверхностью тела (конвективной теплоотдаче). Тепловой баланс на границе тела имеет вид
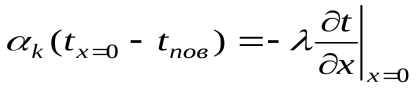 . (1.20)
. (1.20)
Этот случай часто применяют при решении практических задач.
4. В высокотемпературных печах чаще всего передача тепла осуществляется лучеиспусканием. Тогда тепловой баланс на границе может быть описан уравнением
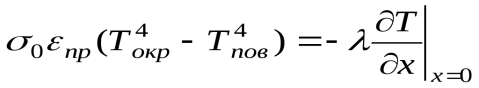
. (1.21)
Если разность температур среды и поверхности невелика и соблюдается неравенство 0,9 <Токр/Тх=0<1,1, то этот случай можно свести к граничным условиям 3-го рода и тогда
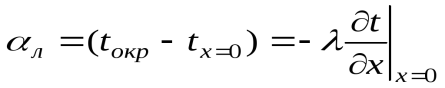 , (1.22)
, (1.22)
где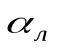 —коэффициент теплоотдачи лучеиспусканием, Вт/(м²·град);
—коэффициент теплоотдачи лучеиспусканием, Вт/(м²·град);
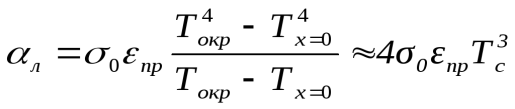 . (1.23)
. (1.23)
Различают два режима распространения тепла в теле: а) при установившемся (стационарном) режиме, когда температурное поле тела не изменяется во времени, т. е. когда температура каждой точки постоянна (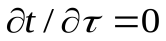 ); б) при неустановившемся (нестационарном) режиме, когда происходит нагрев или охлаждение тела, т. е. когда температурное поле изменяется с течением времени. На рис. 1.4 показан процесс одностороннего прогрева плоской стенки (пластины). Сначала нагревается внутренняя поверхность стенки. Постепенно тепло распространяется все глубже в толщу материала и, наконец, после более или менее продолжительного времени наступает установившийся процесс распространения тепла. Это происходит, когда стенка вполне прогрелась и тепло больше не расходуется на увеличение энтальпии ее материала, а температура ее остается неизменной.
); б) при неустановившемся (нестационарном) режиме, когда происходит нагрев или охлаждение тела, т. е. когда температурное поле изменяется с течением времени. На рис. 1.4 показан процесс одностороннего прогрева плоской стенки (пластины). Сначала нагревается внутренняя поверхность стенки. Постепенно тепло распространяется все глубже в толщу материала и, наконец, после более или менее продолжительного времени наступает установившийся процесс распространения тепла. Это происходит, когда стенка вполне прогрелась и тепло больше не расходуется на увеличение энтальпии ее материала, а температура ее остается неизменной.
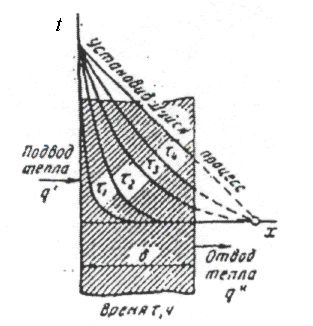
Рис.1.4. Процессы прогрева плоской стенки (пластины).
Кривые показывают распределение температур по истечении времени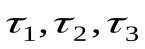 и т. д. от начала нагрева. На практике процессы нагревания и охлаждения в условиях нестационарных режимов встречаются очень часто. Так, в промышленных печах изделия подвергаются нагреву для тепловой обработки материала. Например, стальные слитки нагревают перед прокаткой и ковкой в нагревательных печах. В регенеративных теплообменниках греющей средой сначала нагревается теплоемкая насадка, а затем эта насадка отдает тепло нагреваемой среде. Принцип регенерации используется и в отопительных комнатных печах: в то время, когда они топятся, разогревается кладка, а после закрытия грубы тепло нагретой кладки постепенно распространяется по помещению, где установлена печь.
и т. д. от начала нагрева. На практике процессы нагревания и охлаждения в условиях нестационарных режимов встречаются очень часто. Так, в промышленных печах изделия подвергаются нагреву для тепловой обработки материала. Например, стальные слитки нагревают перед прокаткой и ковкой в нагревательных печах. В регенеративных теплообменниках греющей средой сначала нагревается теплоемкая насадка, а затем эта насадка отдает тепло нагреваемой среде. Принцип регенерации используется и в отопительных комнатных печах: в то время, когда они топятся, разогревается кладка, а после закрытия грубы тепло нагретой кладки постепенно распространяется по помещению, где установлена печь.
8. Стационарные одномерные стационарные задачи теплопроводности
Применим уравнение теплопроводности для решения задач, в которых температура зависит только от одной линейной координаты. Примем, что в прямоугольной системе координат температура будет зависеть только от x, а в цилиндрической и сферической системах координат—только от радиуса. Предполагается, что коэффициент теплопроводности является постоянной величиной, а тепловыделение отсутствует.
Применим общую методику решения, состоящую из двух этапов. На первом этапе из решения соответствующего упрощенного уравнения теплопроводности находится распределение температуры. С этой целью отыскивается аналитическое решение дифференциального уравнения второго порядка. После того как решение дифференциального уравнения записано в общем виде, с помощью двух граничных условий определяются две постоянные интегрирования. На втором этапе с помощью закона Фурье вычисляется кондуктивный тепловой поток через твердое тело.
1.1 Общее понятие термического сопротивления
Математическое выражение закона Гука имеет вид:
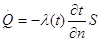
или после разделения переменных
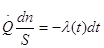 ,
,
интегрируя в пределах изменения пространственной координаты и в соответствующем температурном интервале, получаем
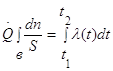 или
или
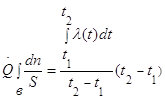
Выражение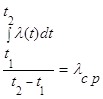
называется среднеинтегральным коэффициентом теплопроводности в интервале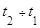 . При линейной зависимости
. При линейной зависимости
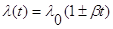
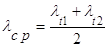
При постоянном: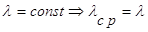
Таким образом, имеем
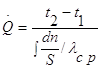
Сравнивая полученное уравнение с выражением закона Ома
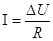 ,
,
получаем уравнение, определяющее термическое сопротивление теплопроводности в общем случае
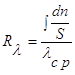 (1.0)
(1.0)
Для получения выражения, определяющего термическое сопротивление конвективного теплообмена, рассмотрим закон Ньютона-Рихмана
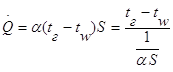
То есть термическое сопротивление конвективного теплообмена определится выражением
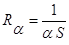 (1.01)
(1.01)
1.2 Прямоугольные координаты
Стационарное одномерное распределение температуры в плоской прямоугольной стенке при отсутствии внутреннего тепловыделения описывается упрощенным уравнением теплопроводности
d2T/dx2 = 0.
Решение этого дифференциального уравнения с использованием двух постоянных интегрирования C1 и С2 имеет вид:
Т (х) = С1x + С2.
Значения этих постоянных можно найти, если заданы два граничных условия. Предположим, что в качестве этих условий заданы температуры на двух поверхностях стенки (рисунке 1.1): Т(0)=T1 и T(b)=T2. Применяя эти граничные условия, получаем следующее распределение безразмерной температуры в стенке:
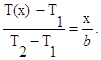 (1.1)
(1.1)
Следовательно, температура изменяется линейно по x. Тепловой поток через стенку определяется законом Фурье:
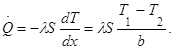 (1.2)
(1.2)
Тепловой поток на единицу площади называется плотностью теплового потока и обозначается q. Для плоской стенки
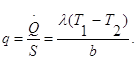
Если записать соотношение (1.2) в форме закона Ома:
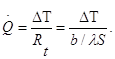 (1.3)
(1.3)
то термическое сопротивление плоской стенки выражается формулой
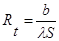 . (1.4)
. (1.4)
Используя общее понятие термического сопротивления теплопроводности, (1.0), получаем аналогичное выражение
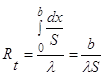
Кондуктивный тепловой поток через плоскую стенку обусловлен перепадом температур поперек стенки, и его распространению противодействует термическое сопротивление, пропорциональное толщине стенки и обратно пропорциональное коэффициенту теплопроводности стенки и площади ее поперечного сечения.
Если кондуктивный перенос тепла осуществляется через составную (многослойную) плоскую стенку, распределение температуры и тепловой поток можно найти, предполагая, что тепло течет по эквивалентной тепловой цепи, представляющей сумму термических сопротивлений, соответствующих отдельным слоям из различных материалов.
В качестве примера тепловой цепи рассмотрим плоскую стенку (индекс 1), покрытую двумя слоями различных изоляционных материалов (индексы 2 и 3). Геометрия задачи показана на рисунке 1.2. Один и тот же тепловой поток проходит последовательно через каждое термическое сопротивление, и, следовательно, тепловая цепь состоит из последовательно соединенных термических сопротивлений. Если известны свойства всех трех материалов, заданы геометрические характеристики и температуры на двух внешних поверхностях, тепловой поток можно найти с помощью соотношения, аналогичного закону Ома:
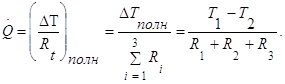 (1.5)
(1.5)
Поскольку тепловой поток через многослойную стенку известен, можно найти температуры на поверхностях раздела материалов, применяя закон Ома для каждого слоя. Например, температуру Тx на поверхности раздела материалов 1 и 2 можно рассчитать по формуле
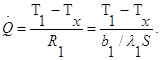 (1.6)
(1.6)
Часто в многослойных стенках слои материалов расположены так, что тепловой поток через них течет скорее параллельно, чем последовательно. В таком случае в тепловую цепь включаются участки из параллельно соединенных термических сопротивлений.
1.Если задается изменение температуры на поверхности тела во времени tпов= f(
2.Если на поверхности тела задана плотность теплового потока, то мы имеем граничные условия второго рода. По закону Фурье
Градиент температуры относится к точке тела, расположенной в непосредственной близости от поверхности тела (х= +0).
3.Граничные условия третьего рода соответствуют случаю конвективного теплообмена с поверхностью тела (конвективной теплоотдаче). Тепловой баланс на границе тела имеет вид
Этот случай часто применяют при решении практических задач.
4. В высокотемпературных печах чаще всего передача тепла осуществляется лучеиспусканием. Тогда тепловой баланс на границе может быть описан уравнением
. (1.21)
Если разность температур среды и поверхности невелика и соблюдается неравенство 0,9 <Токр/Тх=0<1,1, то этот случай можно свести к граничным условиям 3-го рода и тогда
где
Различают два режима распространения тепла в теле: а) при установившемся (стационарном) режиме, когда температурное поле тела не изменяется во времени, т. е. когда температура каждой точки постоянна (

Рис.1.4. Процессы прогрева плоской стенки (пластины).
Кривые показывают распределение температур по истечении времени
8. Стационарные одномерные стационарные задачи теплопроводности
Применим уравнение теплопроводности для решения задач, в которых температура зависит только от одной линейной координаты. Примем, что в прямоугольной системе координат температура будет зависеть только от x, а в цилиндрической и сферической системах координат—только от радиуса. Предполагается, что коэффициент теплопроводности является постоянной величиной, а тепловыделение отсутствует.
Применим общую методику решения, состоящую из двух этапов. На первом этапе из решения соответствующего упрощенного уравнения теплопроводности находится распределение температуры. С этой целью отыскивается аналитическое решение дифференциального уравнения второго порядка. После того как решение дифференциального уравнения записано в общем виде, с помощью двух граничных условий определяются две постоянные интегрирования. На втором этапе с помощью закона Фурье вычисляется кондуктивный тепловой поток через твердое тело.
1.1 Общее понятие термического сопротивления
Математическое выражение закона Гука имеет вид:
или после разделения переменных
интегрируя в пределах изменения пространственной координаты и в соответствующем температурном интервале, получаем
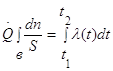 или
или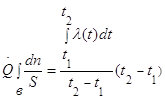
Выражение
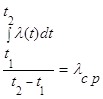
называется среднеинтегральным коэффициентом теплопроводности в интервале
При постоянном:
Таким образом, имеем
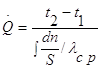
Сравнивая полученное уравнение с выражением закона Ома
получаем уравнение, определяющее термическое сопротивление теплопроводности в общем случае
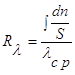 (1.0)
(1.0)Для получения выражения, определяющего термическое сопротивление конвективного теплообмена, рассмотрим закон Ньютона-Рихмана
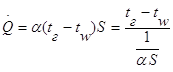
То есть термическое сопротивление конвективного теплообмена определится выражением
1.2 Прямоугольные координаты
Стационарное одномерное распределение температуры в плоской прямоугольной стенке при отсутствии внутреннего тепловыделения описывается упрощенным уравнением теплопроводности
d2T/dx2 = 0.
Решение этого дифференциального уравнения с использованием двух постоянных интегрирования C1 и С2 имеет вид:
Т (х) = С1x + С2.
Значения этих постоянных можно найти, если заданы два граничных условия. Предположим, что в качестве этих условий заданы температуры на двух поверхностях стенки (рисунке 1.1): Т(0)=T1 и T(b)=T2. Применяя эти граничные условия, получаем следующее распределение безразмерной температуры в стенке:
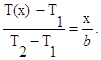 (1.1)
(1.1)Следовательно, температура изменяется линейно по x. Тепловой поток через стенку определяется законом Фурье:
Тепловой поток на единицу площади называется плотностью теплового потока и обозначается q. Для плоской стенки
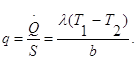
Если записать соотношение (1.2) в форме закона Ома:
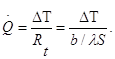 (1.3)
(1.3)то термическое сопротивление плоской стенки выражается формулой
Используя общее понятие термического сопротивления теплопроводности, (1.0), получаем аналогичное выражение
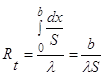
Кондуктивный тепловой поток через плоскую стенку обусловлен перепадом температур поперек стенки, и его распространению противодействует термическое сопротивление, пропорциональное толщине стенки и обратно пропорциональное коэффициенту теплопроводности стенки и площади ее поперечного сечения.
Если кондуктивный перенос тепла осуществляется через составную (многослойную) плоскую стенку, распределение температуры и тепловой поток можно найти, предполагая, что тепло течет по эквивалентной тепловой цепи, представляющей сумму термических сопротивлений, соответствующих отдельным слоям из различных материалов.
В качестве примера тепловой цепи рассмотрим плоскую стенку (индекс 1), покрытую двумя слоями различных изоляционных материалов (индексы 2 и 3). Геометрия задачи показана на рисунке 1.2. Один и тот же тепловой поток проходит последовательно через каждое термическое сопротивление, и, следовательно, тепловая цепь состоит из последовательно соединенных термических сопротивлений. Если известны свойства всех трех материалов, заданы геометрические характеристики и температуры на двух внешних поверхностях, тепловой поток можно найти с помощью соотношения, аналогичного закону Ома:
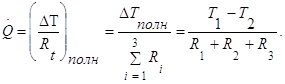 (1.5)
(1.5)Поскольку тепловой поток через многослойную стенку известен, можно найти температуры на поверхностях раздела материалов, применяя закон Ома для каждого слоя. Например, температуру Тx на поверхности раздела материалов 1 и 2 можно рассчитать по формуле
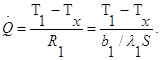 (1.6)
(1.6)Часто в многослойных стенках слои материалов расположены так, что тепловой поток через них течет скорее параллельно, чем последовательно. В таком случае в тепловую цепь включаются участки из параллельно соединенных термических сопротивлений.
