13. 1 и 2 закон термодинамики

Первый закон термодинамики представляет собой закон сохранения энергии применительно к термодинамическим процессам: энергия не исчезает в никуда и не возникает из ничего, а лишь переходит из одного вида в другой в эквивалентных количествах. Примером может послужить переход теплоты (тепловой энергии) в механическую энергию, и наоборот. внутренняя энергия газа

Если к М кг газа, занимающего объем V (м3) при температуре Т подвести при постоянном давлении некоторое количество теплоты dQ, то в результате этого температура газа повысится на dT, а объем – на dV. Повышение температуры связано с увеличением кинетической энергии движения молекул dK.

Увеличение объема сопровождается увеличением расстояния между молекулами и, как следствие, уменьшением потенциальной энергии dH взаимодействия между ними. Кроме того, увеличив объем, газ совершает работу dA по преодолению внешних сил.

Если, кроме указанных, никаких иных процессов в рабочем теле не происходит, то на основании закона сохранения энергии можно записать: dQ = dK + dH + dA.

Сумма dK + dH представляет собой изменение внутренней энергии dU молекул системы в результате подвода теплоты.

Тогда формулу сохранения энергии для термодинамического процесса можно записать в виде: dQ = dU + dA или dQ = dU + pdV.

Это уравнение представляет собой математическое выражение первого закона термодинамики: количество теплоты dQ, подводимое к системе газа, затрачивается на изменение ее внутренней энергии dU и совершение внешней работы dA.

Условно считают, что при dQ > 0 теплота сообщается рабочему телу, а при dQ < 0 теплота отнимается от тела. При dA > 0 система совершает работу (газ расширяется), а при dA < 0 работа совершается над системой (газ сжимается).

Для идеального газа, между молекулами которого нет взаимодействия, изменение внутренней энергии dU полностью определяется изменением кинетической энергии движения (т. е. увеличением скорости молекул), а изменение объема характеризует работу газа по преодолению внешних сил.

Первый закон термодинамики имеет еще одну формулировку: энергия изолированной термодинамической системы остается неизменной независимо от того, какие процессы в ней протекают.

Невозможно построить вечный двигатель первого рода, т. е. периодически действующую машину, которая совершала бы работу без затраты энергии.

Второй закон термодинамики

Первый закон термодинамики описывает количественные соотношения между параметрами термодинамической системы, имеющими место в процессах преобразования тепловой энергии в механическую и наоборот, но не устанавливает условия, при которых эти процессы возможны. Эти условия, необходимые для преобразования одного вида энергии в другой, раскрывает второй закон термодинамики.

---

Существует несколько формулировок этого закона, и каждая из них имеет одинаковое смысловое содержание. Здесь приведены наиболее часто упоминающиеся формулировки второго закона термодинамики.

1. Для превращения теплоты в механическую работу необходимо иметь источник теплоты и холодильник, температура которого ниже температуры источника, т. е. необходим температурный перепад.

2. Нельзя осуществить тепловой двигатель, единственным результатом действия которого было бы превращение теплоты какого-либо тела в работу без того, чтобы часть теплоты не передавалась другим телам.

Из этой формулировки можно сделать вывод, что невозможно построить вечный двигатель, совершающий работу благодаря лишь одному источнику теплоты, поскольку любой, даже самый колоссальный источник теплоты в виде материального тела не способен отдать тепловой энергии больше, чем ему позволяет энтальпия (часть полной энергии тела, которую можно превратить в теплоту, охладив тело до температуры абсолютного нуля).

3. Теплота не может сама по себе переходить от менее нагретого тела к более нагретому без затраты внешней работы.

Как видно, второй закон термодинамики не имеет в своей основе формулярнго содержания, а лишь описывает условия, при которых возможны те или иные термодинамические явления и процессы, подтверждая, по сути, общий закон сохранения энергии.

14. Изопроцессы идеального газа

---

Изопроцессы идеального газа – процессы, при которых один из параметров остаётся неизменным.

       1. Изохорический процесс. Закон Шарля. V = const.

       Изохорическим процессом называется процесс, протекающий при постоянном объёме V. Поведение газа при этом изохорическом процессе подчиняется закону Шарля:

       При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным: P/Т = const.

       График изохорического процесса на РV-диаграмме называется изохорой. Полезно знать график изохорического процесса на РТ- и VT-диаграммах (рис. 1.6).       Уравнение изохоры:

(1.4.1)

 
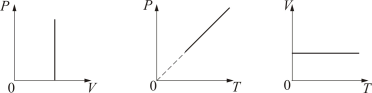
Рис. 1.6

       Если температура газа выражена в градусах Цельсия, то уравнение изохорического процесса записывается в виде

(1.4.2)

где Р₀ – давление при 0 °С, α - температурный коэффициент давления газа равный 1/273 град^-1. График такой зависимости на Рt-диаграмме имеет вид, показанный на рисунке 1.7.

 
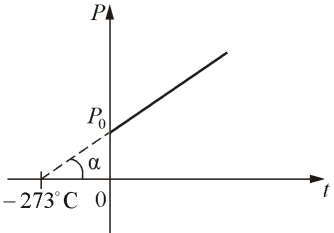
Рис. 1.7

       2. Изобарический процесс. Закон Гей-Люссака. Р = const.

       Изобарическим процессом называется процесс, протекающий при постоянном давлении Р. Поведение газа при изобарическом процессе подчиняется закону Гей-Люссака:

       При постоянном давлении и неизменных значениях массы и газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: 

---

V/T = const.

       График изобарического процесса на VT-диаграмме называется изобарой. Полезно знать графики изобарического процесса на РV- и РT-диаграммах (рис. 1.8).

 
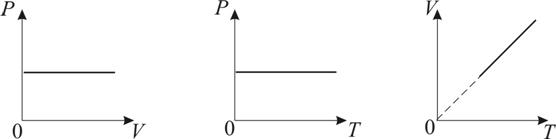
Рис. 1.8

       Уравнение изобары:

.

(1.4.3)

       Если температура газа выражена в градусах Цельсия, то уравнение изобарического процесса записывается в виде

(1.4.4)

где α =1/273 град ^-1- температурный коэффициент объёмного расширения. График такой зависимости на Vt диаграмме имеет вид, показанный на рисунке 1.9.

 
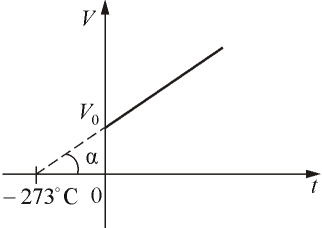
Рис. 1.9

       3. Изотермический процесс. Закон Бойля – Мариотта. T = const.

       Изотермическим процессом называется процесс, протекающий при постоянной температуре Т.

       Поведение идеального газа при изотермическом процессе подчиняется закону Бойля – Мариотта:

       При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.

       График изотермического процесса на РV-диаграмме называется изотермой. Полезно знать графики изотермического процесса на VT- и РT-диаграммах (рис. 1.10).

 
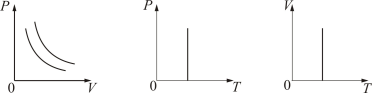
Рис. 1.10

       Уравнение изотермы:

(1.4.5)

---

       4. Адиабатический процесс (изоэнтропийный):

       Адиабатический процесс – термодинамический процесс, происходящий без теплообмена с окружающей средой.

       5. Политропический процесс. Процесс, при котором теплоёмкость газа остаётся постоянной. Политропический процесс – общий случай всех перечисленных выше процессов.

       6. Закон Авогадро. При одинаковых давлениях и одинаковых температурах, в равных объёмах различных идеальных газов содержится одинаковое число молекул. В одном моле различных веществ содержится N_A=6,02·10²³молекул (число Авогадро).

       7. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов:

(1.4.6)

       Парциальное давление Pn – давление, которое оказывал бы данный газ, если бы он один занимал весь объем.

       При  , давление смеси газов:

(1.4.7)

       8. Объединённый газовый закон (Закон Клапейрона).

       В соответствии с законами Бойля – Мариотта (1.4.5) и Гей-Люссака (1.4.3) можно сделать заключение, что для данной массы газа

15. Энтропия

Для удобства рассмотрения многих термодинамических процессов вводится понятие энтропии - приведенной теплоты.

dq = TdS, т.е. dS = — - формально энтропию можно рассматривать как

функцию, полный дифференциал которой определяется приведенным выражением.

Очевидно, что если тепло подводится (dq0), то энтропия возрастает, если отводится - то энтропия убывает. Энтропия не может быть измерена непосредственно, либо косвенным путем. Ее величину определяют в результате расчета непосредственно применяется для вычислений изменений энтропии в термодинамических процессах. Ts-диаграмма

---

Смотрите также файлы

• Контрольный срез по истории Казахстана 11 класс.docx

• Проблемная ситуация. (на доске записано кубань 85).docx

• Итоговый контроль по дисциплине Человек и его права в контексте современной реальности.docx

• Рассказа Кавказский пленник.docx

• Российский государственный социальный университет Итоговый контроль по дисциплине Арттерапевтические технологии в образовании.docx