Файл: Ответы к экзаменационным вопросам по предмету Основы энергетики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.05.2024
Просмотров: 76
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Х = 0), уравнение для безразмерной температуры при Fo > 0,3 приобретает вид
.
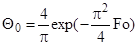Второй предельный случай
:Bi ® 0 (практически при Bi < 0,l). На практике этот случай соответствует охлаждению (или нагреву) тел малой толщины и большой теплопроводности при малом a (например, тонкие металлические пластины, охлаждаемые в воздухе). В этом случае температура по всей толщине тела одна и та же в любой момент времени. Интенсивность процесса охлаждения определяется внешним процессом теплоотдачи – процесс выравнивания температуры внутри тела происходит гораздо интенсивнее, чем отвод теплоты от поверхности. В результате безразмерная температура всех точек пластины определяется уравнением
Q = ехр(-Bi×Fo).
Определение температуры тел ограниченных размеров
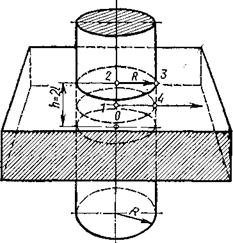Рассмотрим цилиндр конечной длины. Его можно представить как тело, образованное пересечением безграничного цилиндра радиусом R с неограниченной пластиной толщиной h = 2l. Безразмерная температура любой точки ограниченного цилиндра представляет собой произведение безразмерных температур в соответствующих точках безграничных цилиндра и пластины, т. е.
Q = QцQпл,
где в Q – искомая безразмерная температура; Qц = fц(Вiц, Foц, r/R);Qпл = fпл(Вiпл, Foпл, х/l).Соответственно Biu = aR/l; Foц = аt/R2; Biпл = al/l; Foпл = аt/l2.
Величины Qц иQпл могут быть найдены по графикам с учетом расположения рассматриваемой точки в безграничном теле. Так, для точки 1 (рис.)величина Qц находится по графику для центральных точек неограниченного цилиндра, а величина Qпл – по графику для средней плоскости пластины. Для точки 2величина Qц определяется по тому же графику, что и для точки 1, а Qпл – по графику для поверхностных точек пластины. Для точки 3обе величины находятся по графикам для поверхностных точек цилиндра и пластины. Для точки 4величина Qц определяется по графику для поверхностных точек цилиндра, а величина Qпл – по графику для средней плоскости пластины. Перечисленные четыре точки являются характерными для ограниченного цилиндра. Температуры остальных точек ограниченного цилиндра по графикам не могут быть найдены, но для их определения можно воспользоваться соответствующими формулами.
Аналогичные рассуждения справедливы и для параллелепипеда,но его следует рассматривать как тело, образованное пересечением трех неограниченных пластин.
Регулярный режим охлаждения (нагревания) тел
При значении Fo > 0,3 в выражениях типа (1) достаточно ограничиться одним первым членом ряда. В этом случае для пластины
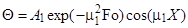. (2)
Режим охлаждения (или нагрева), определяемый формулой (2), называется регулярным. Этот результат обобщается и на более сложные задачи охлаждения (нагрева) тел любой геометрической формы при условии tж и a = const:
,
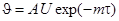где m – темп охлаждения, [1/с].
В этом случае начальные условия начинают играть второстепенную роль, и процесс полностью определяется только условиями охлаждения на границе тела и среды, физическими свойствами тела, его геометрической формой и размерами.
Логарифмируя последнее уравнение, получаем:
lnJ = ln(AU) – тt, или lnJ = -тt + С(x, y, z).
Из последнего уравнения следует, что натуральный логарифм избыточной температуры для всех точек тела изменяется во времени по линейному закону. Если продифференцировать это выражение по времени получим:
.
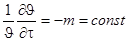В левой части уравнения стоит выражение для относительной скорости изменения температуры, и оно равняется постоянному значению т,не зависящему ни от координат, ни от времени. Следовательно, темп охлаждения характеризует относительную скорость изменения температуры в теле и зависит только от физических свойств тела, процесса охлаждения на его поверхности, геометрической формы и размеров тела.
Если экспериментально определить изменение избыточной температуры Jво времени t и построить зависимость в полулогарифмических координатах, то темп охлаждения в стадии регулярного режима найдется как
.
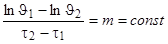Выражение для зависимости темпа охлаждения т от физических свойств тела, его геометрической формы и размеров, а также условий теплообмена на поверхности тела можно найти из анализа теплового баланса. В результате получим:
,
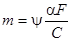где С – полная теплоемкость тела;
y = JF/JV – коэффициент неравномерности распределения температуры в теле;
JF, JV – средние по поверхности и по объему температуры тела.
Из уравнения следует, что темп охлаждения т, однородного тела при конечном значении коэффициента теплоотдачи a пропорционален коэффициенту теплоотдачи, поверхности тела и обратно пропорционален его теплоемкости (первая теорема Кондратьева ).
Коэффициент y зависит от числа Bi, учитывающего условия протекания процесса на поверхности тела. Рассмотрим два предельных случая:
а) Bi ® 0 (практически Bi < 0,1). Это условие соответствует внешней задаче, когда распределение температуры в теле не зависит от его размеров и физических свойств и, следовательно, усредненные по поверхности и объему температуры будут одинаковы. Коэффициент неравномерности распределения температуры в теле y = 1.
б) Bi ® ¥ (практически Bi > 100). При этом условии задача становится внутренней, и процесс охлаждения определяется только размерами тела и его физическими свойствами. В силу большой интенсивности теплообмена температура на поверхности тела принимает постоянное значение, равное температуре окружающей среды. Коэффициент неравномерности распределения температуры y = 0.
При Bi ® ¥, или, что то же, a ® ¥, темп охлаждения т становится прямо пропорциональным коэффициенту температуропроводности тела а (вторая теорема Кондратьева):
.
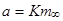Коэффициент пропорциональности К зависит от геометрической формы и размеров тела и определяется в зависимости от формы тела по выражениям:
для шара радиусом r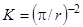
;
для параллелепипеда с длиной граней l1, l2, l3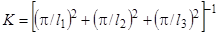
;
для цилиндра длиной l и радиусом r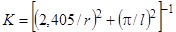
.
На основе теории регулярного режима разработаны различные экспериментальные методики определения теплофизических характеристик материалов.
11. Конвективный теплообмен
Под конвекцией понимают движение микрочастиц относительно друг друга. Любое движение связано с переносом кинетической энергии, а следовательно с изменением температуры. Поэтому, если среда имеет неравномерную температуру, то процесс конвекции будет направлен на ее выравнивание по всему объему.
В зависимости от причин вызывающих движение частиц жидкости или газа, различают два вида конвекции свободную и вынужденную. Свободная конвекция (естественная) – это движение частиц за счет действия на них подъемной силы в результате разности плотности. Интенсивность такой конвекции будет зависеть от рода вещества, разности температуры отдельных частиц вещества и от объема пространства, где происходит движение частиц. Вынужденная (принудительная или искусственная) конвекция вызывается работой посторонних возбудителей (вентилятор, насос и пр.) и возникает он в результате разности давлений, создаваемой этими возбудителями.
Большое значение в интенсивности конвекции имеет режим движения жидкости или газа. Различают два режима движения: ламинарный и турбулентный.
Ламинарный режим движения характеризуется параллельным перемещением слоев жидкости относительно друг друга. Профиль скоростей, взятый по сечению канала, при таком движении имеет вид правильной параболы (рис. 2.6, а). Теплообмен в потоке жидкости не интенсивный и осуществляется в основном за счет теплопроводности слоев.
Турбулентный режим движения характеризуется непостоянством скорости отдельных частиц. Движение представляется вихревым, пульсирующим и прерывистым. Профиль скоростей, взятый по сечению канала, имеет вид усеченной параболы (рис. 2.6, б). Интенсивность теплообмена при таком движении очень высока, так как жидкость постоянно перемешивается.
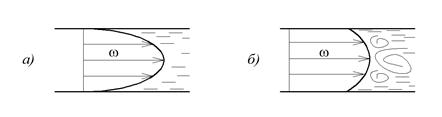
Рис.2.6. Профили скоростей при ламинарном режиме течения жидкости (а)
и при турбулентном течении жидкости (б)
Переход от одного режима движения жидкости к другому осуществляется при достижении критического значения числа Рейнольдса:
.
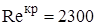Число Рейнольдса определяется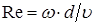
.Второй предельный случай
:Bi ® 0 (практически при Bi < 0,l). На практике этот случай соответствует охлаждению (или нагреву) тел малой толщины и большой теплопроводности при малом a (например, тонкие металлические пластины, охлаждаемые в воздухе). В этом случае температура по всей толщине тела одна и та же в любой момент времени. Интенсивность процесса охлаждения определяется внешним процессом теплоотдачи – процесс выравнивания температуры внутри тела происходит гораздо интенсивнее, чем отвод теплоты от поверхности. В результате безразмерная температура всех точек пластины определяется уравнением
Q = ехр(-Bi×Fo).
Определение температуры тел ограниченных размеров
Рассмотрим цилиндр конечной длины. Его можно представить как тело, образованное пересечением безграничного цилиндра радиусом R с неограниченной пластиной толщиной h = 2l. Безразмерная температура любой точки ограниченного цилиндра представляет собой произведение безразмерных температур в соответствующих точках безграничных цилиндра и пластины, т. е.Q = QцQпл,
где в Q – искомая безразмерная температура; Qц = fц(Вiц, Foц, r/R);Qпл = fпл(Вiпл, Foпл, х/l).Соответственно Biu = aR/l; Foц = аt/R2; Biпл = al/l; Foпл = аt/l2.
Величины Qц иQпл могут быть найдены по графикам с учетом расположения рассматриваемой точки в безграничном теле. Так, для точки 1 (рис.)величина Qц находится по графику для центральных точек неограниченного цилиндра, а величина Qпл – по графику для средней плоскости пластины. Для точки 2величина Qц определяется по тому же графику, что и для точки 1, а Qпл – по графику для поверхностных точек пластины. Для точки 3обе величины находятся по графикам для поверхностных точек цилиндра и пластины. Для точки 4величина Qц определяется по графику для поверхностных точек цилиндра, а величина Qпл – по графику для средней плоскости пластины. Перечисленные четыре точки являются характерными для ограниченного цилиндра. Температуры остальных точек ограниченного цилиндра по графикам не могут быть найдены, но для их определения можно воспользоваться соответствующими формулами.
Аналогичные рассуждения справедливы и для параллелепипеда,но его следует рассматривать как тело, образованное пересечением трех неограниченных пластин.
Регулярный режим охлаждения (нагревания) тел
При значении Fo > 0,3 в выражениях типа (1) достаточно ограничиться одним первым членом ряда. В этом случае для пластины
. (2)Режим охлаждения (или нагрева), определяемый формулой (2), называется регулярным. Этот результат обобщается и на более сложные задачи охлаждения (нагрева) тел любой геометрической формы при условии tж и a = const:
,где m – темп охлаждения, [1/с].
В этом случае начальные условия начинают играть второстепенную роль, и процесс полностью определяется только условиями охлаждения на границе тела и среды, физическими свойствами тела, его геометрической формой и размерами.
Логарифмируя последнее уравнение, получаем:
lnJ = ln(AU) – тt, или lnJ = -тt + С(x, y, z).
Из последнего уравнения следует, что натуральный логарифм избыточной температуры для всех точек тела изменяется во времени по линейному закону. Если продифференцировать это выражение по времени получим:
.В левой части уравнения стоит выражение для относительной скорости изменения температуры, и оно равняется постоянному значению т,не зависящему ни от координат, ни от времени. Следовательно, темп охлаждения характеризует относительную скорость изменения температуры в теле и зависит только от физических свойств тела, процесса охлаждения на его поверхности, геометрической формы и размеров тела.
Если экспериментально определить изменение избыточной температуры Jво времени t и построить зависимость в полулогарифмических координатах, то темп охлаждения в стадии регулярного режима найдется как
.Выражение для зависимости темпа охлаждения т от физических свойств тела, его геометрической формы и размеров, а также условий теплообмена на поверхности тела можно найти из анализа теплового баланса. В результате получим:
,где С – полная теплоемкость тела;
y = JF/JV – коэффициент неравномерности распределения температуры в теле;
JF, JV – средние по поверхности и по объему температуры тела.
Из уравнения следует, что темп охлаждения т, однородного тела при конечном значении коэффициента теплоотдачи a пропорционален коэффициенту теплоотдачи, поверхности тела и обратно пропорционален его теплоемкости (первая теорема Кондратьева ).
Коэффициент y зависит от числа Bi, учитывающего условия протекания процесса на поверхности тела. Рассмотрим два предельных случая:
а) Bi ® 0 (практически Bi < 0,1). Это условие соответствует внешней задаче, когда распределение температуры в теле не зависит от его размеров и физических свойств и, следовательно, усредненные по поверхности и объему температуры будут одинаковы. Коэффициент неравномерности распределения температуры в теле y = 1.
б) Bi ® ¥ (практически Bi > 100). При этом условии задача становится внутренней, и процесс охлаждения определяется только размерами тела и его физическими свойствами. В силу большой интенсивности теплообмена температура на поверхности тела принимает постоянное значение, равное температуре окружающей среды. Коэффициент неравномерности распределения температуры y = 0.
При Bi ® ¥, или, что то же, a ® ¥, темп охлаждения т становится прямо пропорциональным коэффициенту температуропроводности тела а (вторая теорема Кондратьева):
.Коэффициент пропорциональности К зависит от геометрической формы и размеров тела и определяется в зависимости от формы тела по выражениям:
для шара радиусом r
;для параллелепипеда с длиной граней l1, l2, l3
;для цилиндра длиной l и радиусом r
.На основе теории регулярного режима разработаны различные экспериментальные методики определения теплофизических характеристик материалов.
11. Конвективный теплообмен
Под конвекцией понимают движение микрочастиц относительно друг друга. Любое движение связано с переносом кинетической энергии, а следовательно с изменением температуры. Поэтому, если среда имеет неравномерную температуру, то процесс конвекции будет направлен на ее выравнивание по всему объему.
В зависимости от причин вызывающих движение частиц жидкости или газа, различают два вида конвекции свободную и вынужденную. Свободная конвекция (естественная) – это движение частиц за счет действия на них подъемной силы в результате разности плотности. Интенсивность такой конвекции будет зависеть от рода вещества, разности температуры отдельных частиц вещества и от объема пространства, где происходит движение частиц. Вынужденная (принудительная или искусственная) конвекция вызывается работой посторонних возбудителей (вентилятор, насос и пр.) и возникает он в результате разности давлений, создаваемой этими возбудителями.
Большое значение в интенсивности конвекции имеет режим движения жидкости или газа. Различают два режима движения: ламинарный и турбулентный.
Ламинарный режим движения характеризуется параллельным перемещением слоев жидкости относительно друг друга. Профиль скоростей, взятый по сечению канала, при таком движении имеет вид правильной параболы (рис. 2.6, а). Теплообмен в потоке жидкости не интенсивный и осуществляется в основном за счет теплопроводности слоев.
Турбулентный режим движения характеризуется непостоянством скорости отдельных частиц. Движение представляется вихревым, пульсирующим и прерывистым. Профиль скоростей, взятый по сечению канала, имеет вид усеченной параболы (рис. 2.6, б). Интенсивность теплообмена при таком движении очень высока, так как жидкость постоянно перемешивается.
Рис.2.6. Профили скоростей при ламинарном режиме течения жидкости (а)
и при турбулентном течении жидкости (б)
Переход от одного режима движения жидкости к другому осуществляется при достижении критического значения числа Рейнольдса:
.Число Рейнольдса определяется