ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 21
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пример 4
Построить область интегрирования и изменить порядок интегрирования
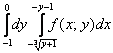
Это пример для самостоятельного решения. Пример не очень сложный, но обратите внимание, что порядок обхода изначально задан вторым способом! Что делать в подобных случаях? Во-первых, возникает трудность с чертежом, поскольку чертить график обратной функции наподобие непривычно даже мне самому. Я рекомендую следующий порядок действий: сначала из получаем «обычную» функцию (выражаем «игрек» через «икс»). Далее строим график этой «обычной» функции (всегда можно построить хотя бы поточечно). Аналогично поступаем с более простой линейной функцией: из выражаем «игрек» и проводим прямую.
Анализируем исходные пределы интегрирования: входим слева в область через и выходим через . При этом все дела происходят в «игрековой» полосе от –1 до 0. После того, как вы определили на чертеже область интегрирования, сменить порядок обхода не составит особого труда. Примерный образец оформления решения в конце урока.
Похожий пример я еще разберу подробнее чуть позже.
Даже если вы всё отлично поняли, пожалуйста, не торопитесь переходить непосредственно к вычислениям двойного интеграла. Порядок обхода – вещь коварная, и очень важно немного набить руку на данной задаче, тем более, я еще не всё рассмотрел!
В предыдущих четырёх примерах область интегрирования находилась целиком в 1-й, 2-й, 3-й и 4-й координатных четвертях. Всегда ли это так? Нет, естественно.
Пример 5
Изменить порядок интегрирования
Решение: Выполним чертёж, при этом, график функции фактически представляет собой кубическую параболу, просто она «лежит на боку»:
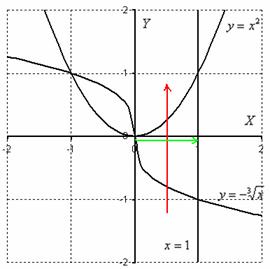
Порядок обхода области, который соответствует повторным интегралам , обозначен стрелками. Обратите внимание, что в ходе выполнения чертежа прорисовалась еще одна ограниченная фигура (левее оси ординат). Поэтому следует быть внимательным при определении области интегрирования – за область можно ошибочно принять не ту фигуру.
Перейдем к обратным функциям:
– нужная нам правая ветвь параболы;
Изменим порядок обхода области. Как вы помните, при втором способе обхода, область нужно сканировать лазерным лучом слева направо. Но тут наблюдается интересная вещь:
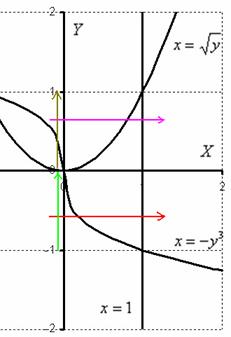
Как поступать в подобных случаях? В таких случаях следует разделить область интегрирования на две части и для каждой из частей составить свои повторные интегралы:
1) Если «игрек» изменяется от –1 до 0 (зеленая стрелка), то луч входит в область через кубическую параболу и выходит через прямую (красная стрелка). Поэтому порядок обхода области будет следующим:
И соответствующие повторные интегралы:
2) Если «игрек» изменяется от 0 до 1 (коричневая стрелка), то луч входит в область через ветвь параболы и выходит через ту же прямую (малиновая стрелка). Следовательно, порядок обхода области будет следующим:
И соответствующие повторные интегралы:
У определенных и кратных интегралов есть весьма удобное свойство аддитивности, то есть, их можно сложить, что в данном случае и следует сделать:
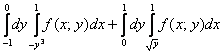– а вот и наш обход области вторым способом в виде суммы двух интегралов.Ответ записываем так:
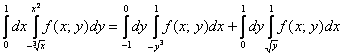
Какой порядок обхода выгоднее? Конечно тот, который был дан в условии задачи – вычислений будет в два раза меньше!
Пример 6
Изменить порядок интегрирования
Это пример для самостоятельного решения. В нём присутствуют полуокружности, разборки с которыми были подробно рассмотрены в Примере 3. Примерный образец оформления решения в конце урока.
А сейчас обещанная задача, когда изначально задан второй способ обхода области:
Пример 7
Изменить порядок интегрирования
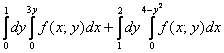
Решение: Когда порядок обхода задан вторым способом, то перед построением чертежа целесообразно перейти к «обычным» функциям. В данном примере присутствуют два пациента для преобразования: и .
С линейной функцией всё просто:
График функции представляется собой параболу с претензией на каноничность.
Выразим «игрек» через «икс»:
Получаем две ветви параболы: и . Какую из них выбрать? Проще всего сразу выполнить чертёж. И даже если вы крепко позабыли материал аналитической геометрии о параболе, то всё равно обе ветви можно построить поточечно:
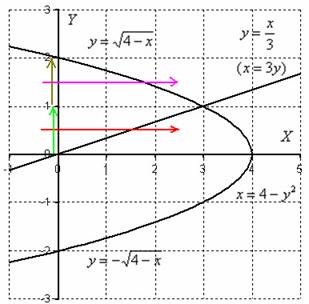
Еще раз обращаю внимание на тот факт, что на данном чертеже получилось несколько плоских фигур, и очень важно выбрать нужную фигуру! В выборе искомой фигуры как раз помогут пределы интегрирования исходных интегралов:
, при этом не забывайте, что обратная функция задаёт всю параболу.Стрелочки, которыми обозначен обход фигуры, в точности соответствуют пределам интегрирования интегралов
.Довольно быстро вы научитесь проводить такой анализ мысленно и находить нужную область интегрирования.
Когда фигура найдена, заключительная часть решения, в общем-то, очень проста, меняем порядок обхода области:
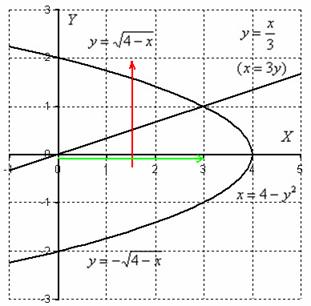
Обратные функции уже найдены, и требуемый порядок обхода области:
Ответ:
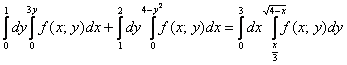
Заключительный пример параграфа для самостоятельного решения:
Пример 8
Изменить порядок интегрирования
Полное решение и ответ в конце урока.
Как вычислить площадь плоской фигуры с помощью двойного интеграла?
Начинаем рассматривать собственно процесс вычисления двойного интеграла и знакомиться с его геометрическим смыслом.
Двойной интеграл численно равен площади плоской фигуры (области интегрирования). Это простейший вид двойного интеграла, когда функция двух переменных равна единице: .
Сначала рассмотрим задачу в общем виде. Сейчас вы немало удивитесь, насколько всё действительно просто! Вычислим площадь плоской фигуры , ограниченной линиями . Для определённости считаем, что на отрезке . Площадь данной фигуры численно равна:
Изобразим область на чертеже:
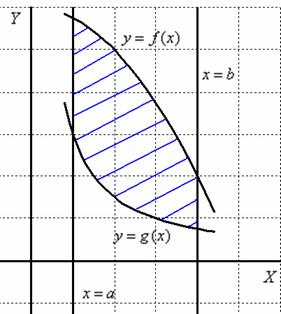
Выберем первый способ обхода области:
Таким образом:
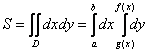
И сразу важный технический приём: повторные интегралы можно считать по отдельности. Сначала внутренний интеграл, затем – внешний интеграл. Данный способ настоятельно рекомендую начинающим в теме чайникам.
1) Вычислим внутренний интеграл, при этом интегрирование проводится по переменной «игрек»:
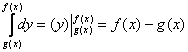
Неопределённый интеграл тут простейший, и далее используется банальная формула Ньютона-Лейбница, с той лишь разницей, что пределами интегрирования являются не числа, а функции. Сначала подставили в «игрек» (первообразную функцию) верхний предел, затем – нижний предел
2) Результат, полученный в первом пункте необходимо подставить во внешний интеграл:
Более компактная запись всего решения выглядит так:
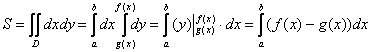
Полученная формула – это в точности рабочая формула для вычисления площади плоской фигуры с помощью «обычного» определённого интеграла! Смотрите урок Вычисление площади с помощью определенного интеграла, там она на каждом шагу!
То есть, задача вычисления площади с помощью двойного интеграла мало чем отличается от задачи нахождения площади с помощью определённого интеграла! Фактически это одно и тоже!
Соответственно, никаких трудностей возникнуть не должно! Я рассмотрю не очень много примеров, так как вы, по сути, неоднократно сталкивались с данной задачей.
Пример 9
С помощью двойного интеграла, вычислить площадь плоской фигуры , ограниченной линиями ,
Решение: Изобразим область на чертеже:
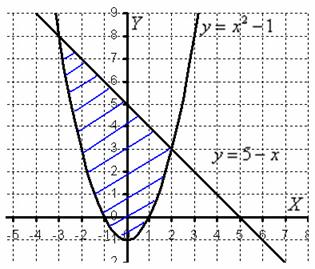
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
Выберем следующий порядок обхода области:
Здесь и далее я не буду останавливаться на том, как выполнять обход области, поскольку в первом параграфе были приведены очень подробные разъяснения.
Таким образом:
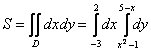
Как я уже отмечал, начинающим лучше вычислять повторные интегралы по отдельности, этого же метода буду придерживаться и я:
1) Сначала с помощью формулы Ньютона-Лейбница разбираемся с внутренним интегралом:
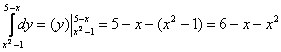
2) Результат, полученный на первом шаге, подставляем во внешний интеграл:
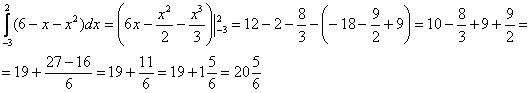
Пункт 2 – фактически нахождение площади плоской фигуры с помощью определённого интеграла.
Ответ:
Вот такая вот глупая и наивная задача.
Любопытный пример для самостоятельного решения:
Пример 10
С помощью двойного интеграла, вычислить площадь плоской фигуры , ограниченной линиями , ,
Примерный образец чистового оформления решения в конце урока.
В Примерах 9-10 значительно выгоднее использовать первый способ обхода области, любознательные читатели, кстати, могут изменить порядок обхода и вычислить площади вторым способом. Если не допустите ошибку, то, естественно, получатся те же самые значения площадей.
Но в ряде случаев более эффективен второй способ обхода области, и в заключение курса молодого ботана рассмотрим ещё пару примеров на эту тему:
Пример 11
С помощью двойного интеграла, вычислить площадь плоской фигуры , ограниченной линиями ,
Решение: нас с нетерпением ждут две параболы, которые лежат на боку.
Как проще всего сделать чертёж?
Представим параболу в виде двух функций:
– верхняя ветвь и – нижняя ветвь.
Аналогично, представим параболу в виде верхней и нижней ветвей.
Далее рулит поточечное построение графиков, в результате чего получается вот такая причудливая фигура:
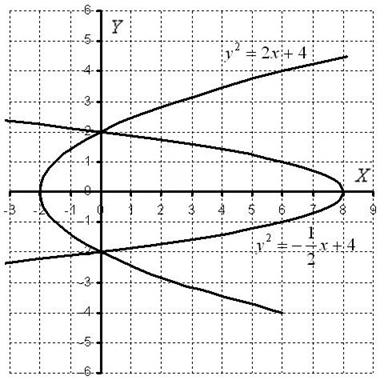
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
Что будет, если мы выберем первый способ обхода области? Во-первых, данную область придётся разделить на две части. А во-вторых, мы будем наблюдать сию печальную картину:
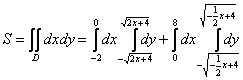. Интегралы, конечно, не сверхсложного уровня, но… существует старая математическая присказка: кто с корнями дружен, тому зачёт не нужен.Поэтому из недоразумения, которое дано в условии, выразим обратные функции:
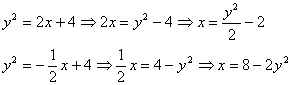
Обратные функции в данном примере обладают тем преимуществом, что задают сразу всю параболу целиком без всяких там