ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 22
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, а полярный угол не определен.
Пусть декартовая полуось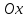 совпадает с полярным лучом .Декартовые координаты выражаются через полярные по формулам
совпадает с полярным лучом .Декартовые координаты выражаются через полярные по формулам 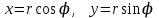 .
.
Полярные координаты выражаются через декартовые
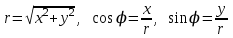 .
.
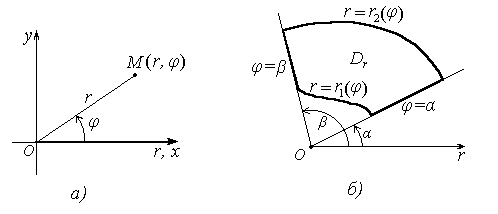
Пусть область D в декартовых координатах преобразуется в область Dr в полярных координатах согласно формулам (10).
Якобиан в данном случае равен:
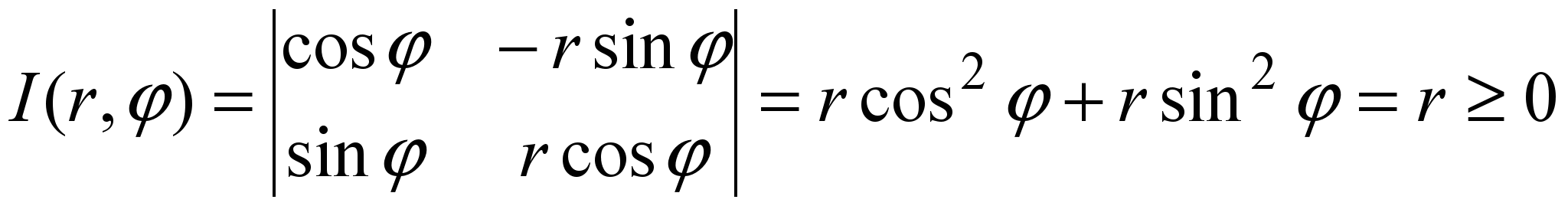
Тогда интеграл (2) преобразуется в двойной интеграл в полярных координатах по формуле
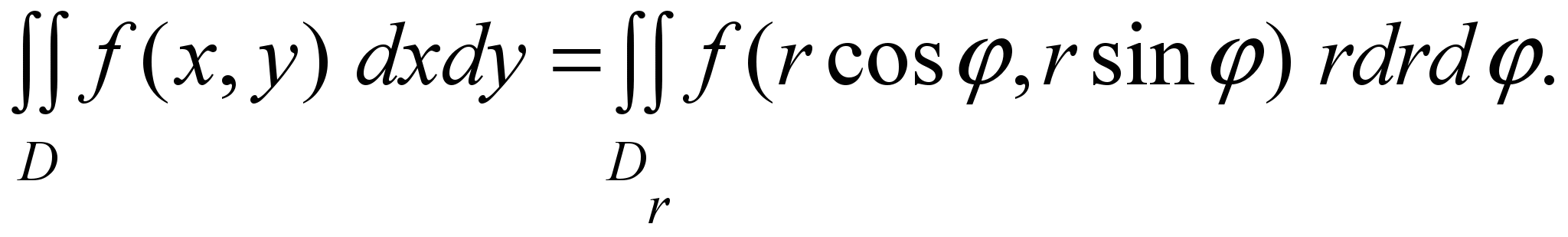 (16)
(16)
Двойной интеграл (16) вычисляется переходом к повторному интегралу в полярных координатах. Пусть область Dr имеет вид
Dr= { (r, φ) : α ≤φ≤ β, r1(φ)≤ r≤ r2 (φ)},
где лучи φ= α и φ= β ограничивают сектор, в котором находится фигура Dr , кривые r = r1(φ), r = r2 (φ) ограничивают ее в этом секторе. Тогда
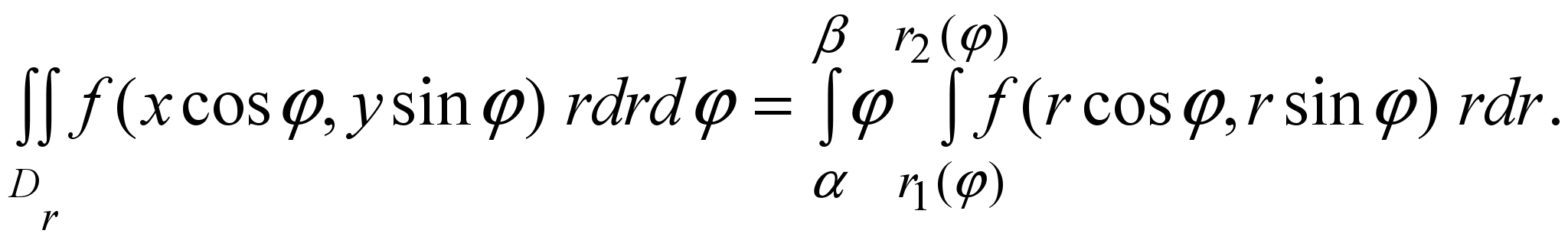 (17)
(17)
Замечание. При расстановке пределов интегрирования в повторном интеграле нужно учесть, что изменение полярного угла определяется поворотом луча, исходящего из начала O вокруг него против хода часовой стрелки, а изменение полярного радиуса определяется движением точки вдоль луча в сторону его возрастания.
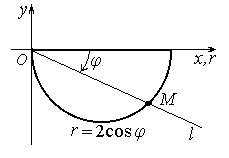
Рисунок 5
Примеры. 1). Расставить пределы интегрирования в повторном интеграле в полярных координатах
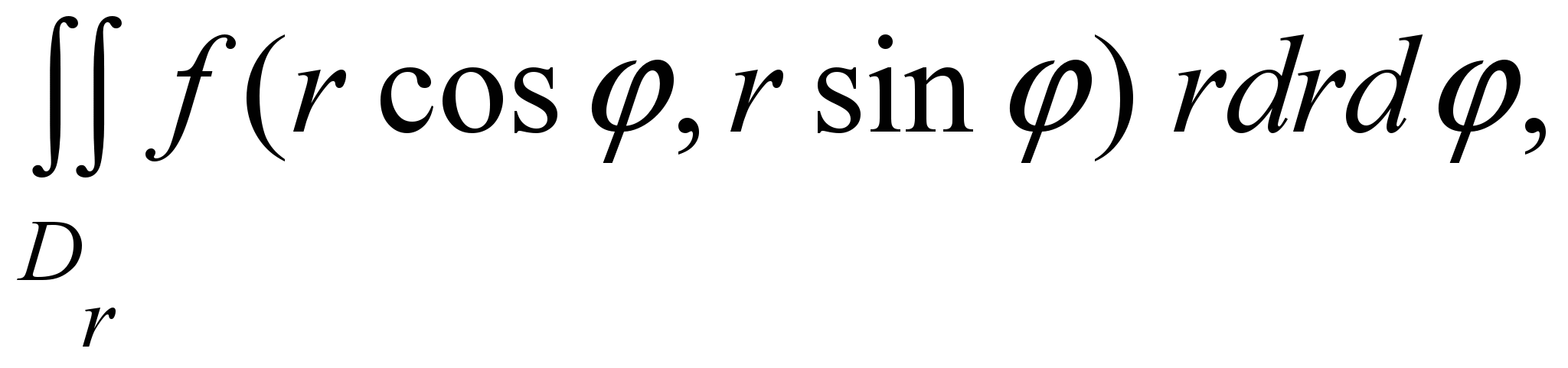
где Dr полукруг из рисунка 5.
Решение. Все точки этого полукруга будут охвачены, если луч Оl будет поворачиваться от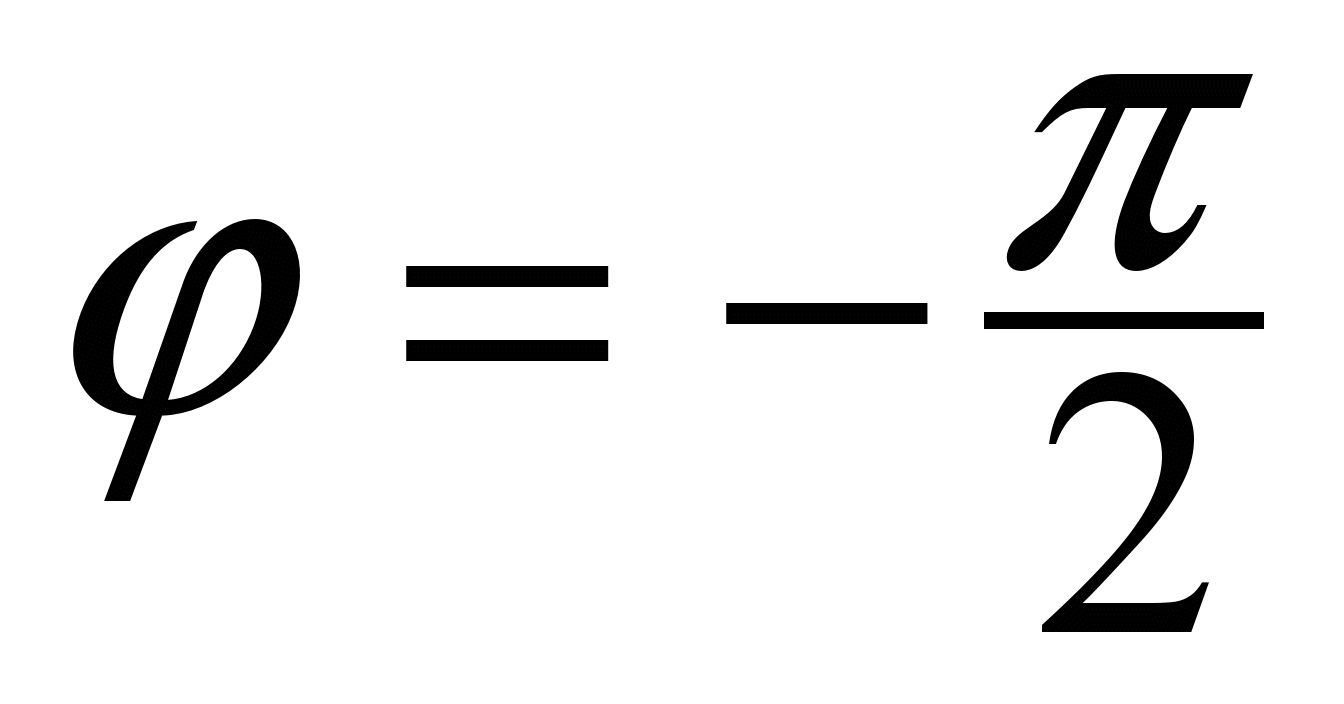 до φ = 0 против хода часовой стрелки. Значит,
до φ = 0 против хода часовой стрелки. Значит, 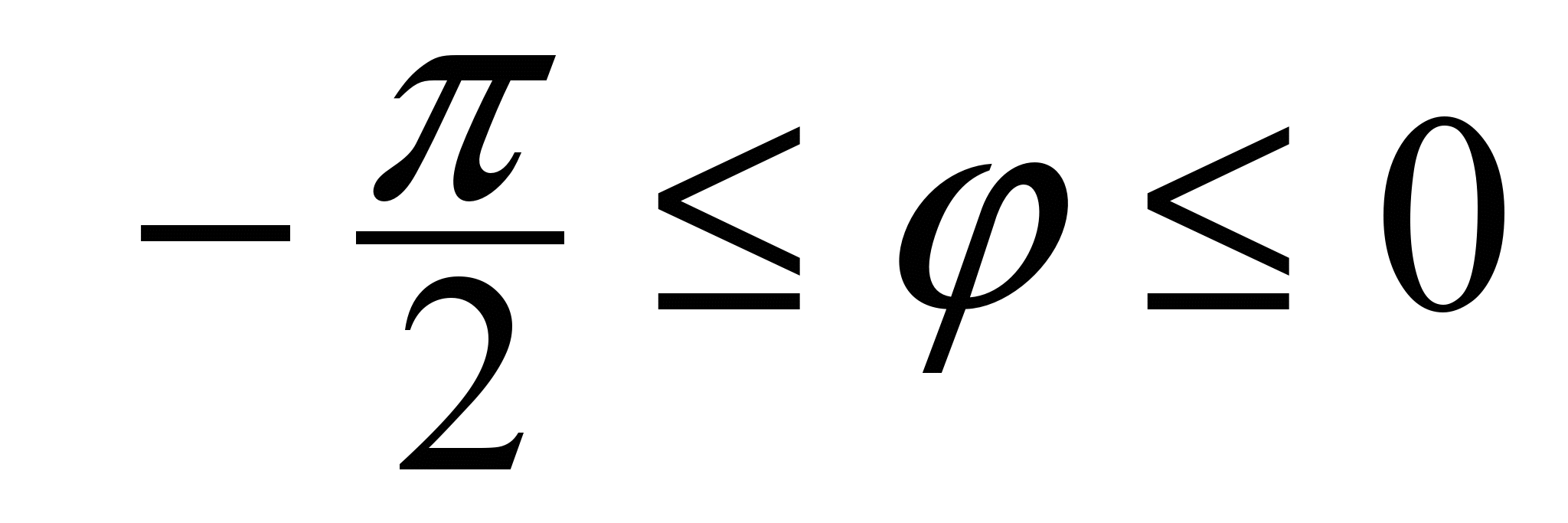 . Пусть теперь луч Оl имеет полярный угол
. Пусть теперь луч Оl имеет полярный угол 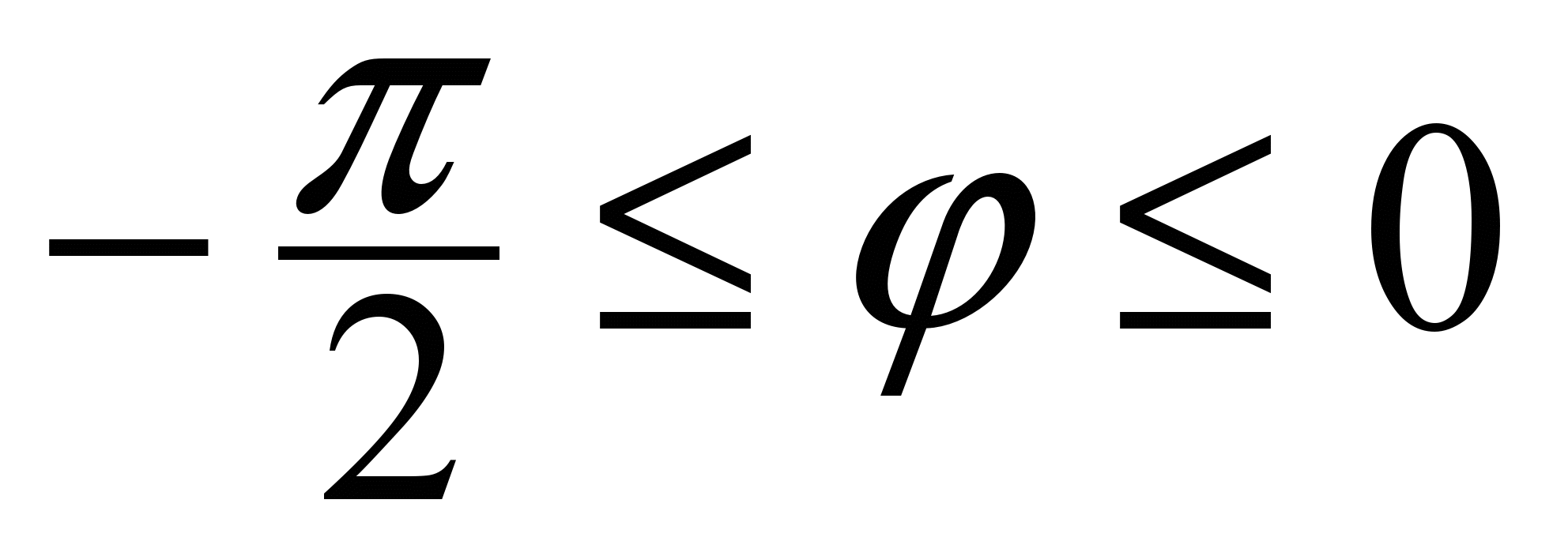 . Тогда при движении точки полукруга по лучу Оl (рис. 5) от точки О до точки Mполярный радиус rизменяется от 0 до координаты r=2cosφ точки M. Значит,
. Тогда при движении точки полукруга по лучу Оl (рис. 5) от точки О до точки Mполярный радиус rизменяется от 0 до координаты r=2cosφ точки M. Значит,
0 ≤ r ≤ 2cos φ. Таким образом, Dr ={(r, φ):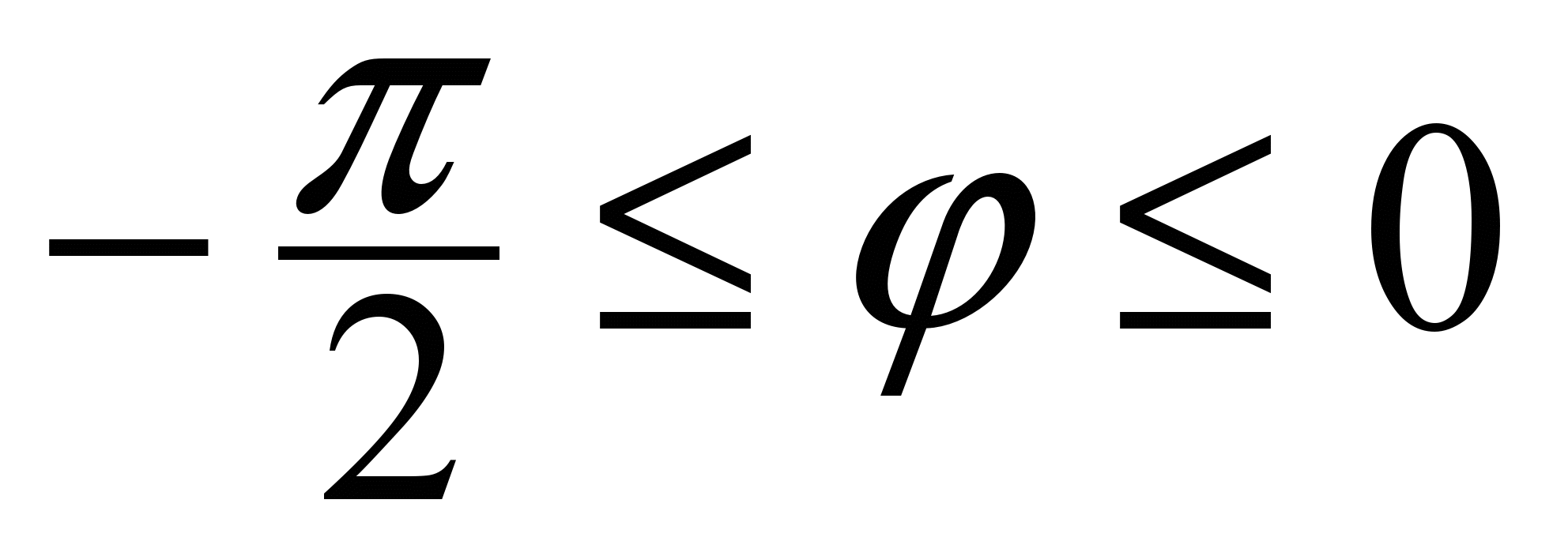 , 0 ≤ r ≤ 2 cos φ}. Следовательно,
, 0 ≤ r ≤ 2 cos φ}. Следовательно,
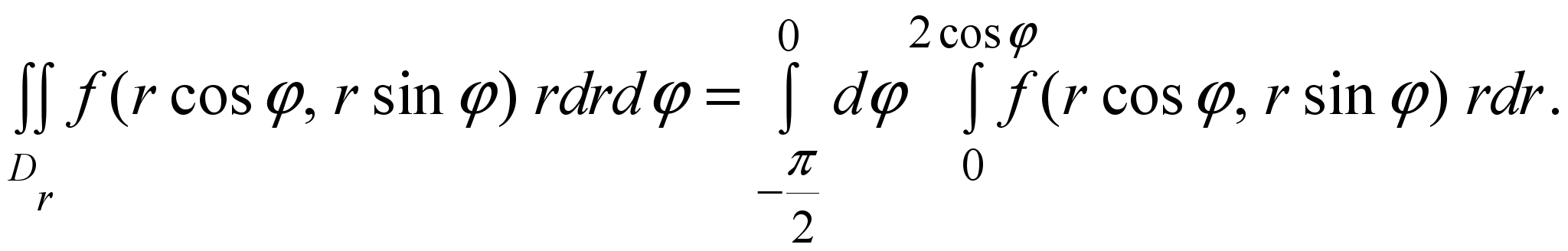
2) Вычислить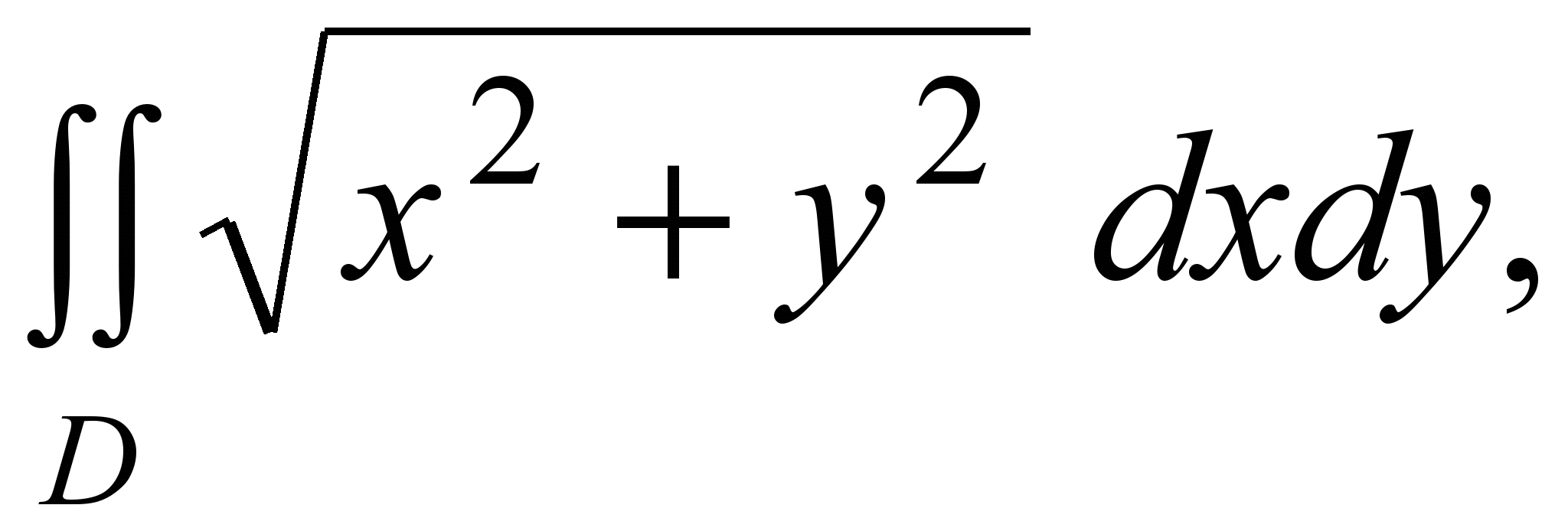 где D ={(x, y): x2+ y22x ≤0, y≤0}.
где D ={(x, y): x2+ y22x ≤0, y≤0}.
Решение. Подставим в уравнение окружности x2+y22x =0 полярные координаты (9) и преобразуем: r22 rcosφ= 0 r =2cosφ. Мы получили уравнение полуокружности в полярных координатах из рисунка 5. Поскольку y≤0, то D полукруг из примера 3. Расставим пределы интегрирования как в этом примере и вычислим:
r =2cosφ. Мы получили уравнение полуокружности в полярных координатах из рисунка 5. Поскольку y≤0, то D полукруг из примера 3. Расставим пределы интегрирования как в этом примере и вычислим:
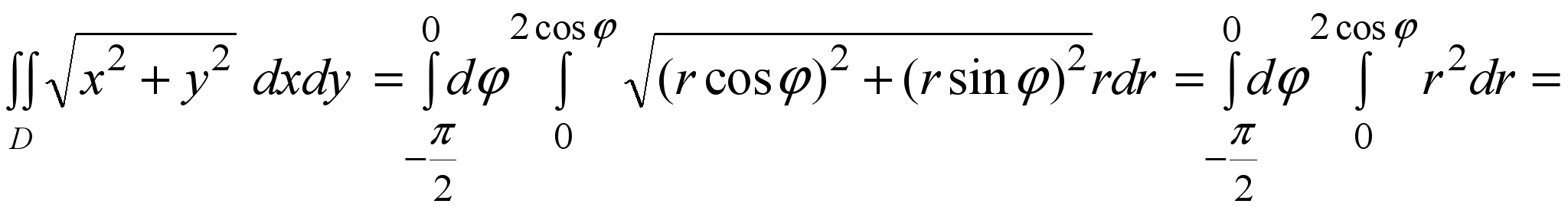
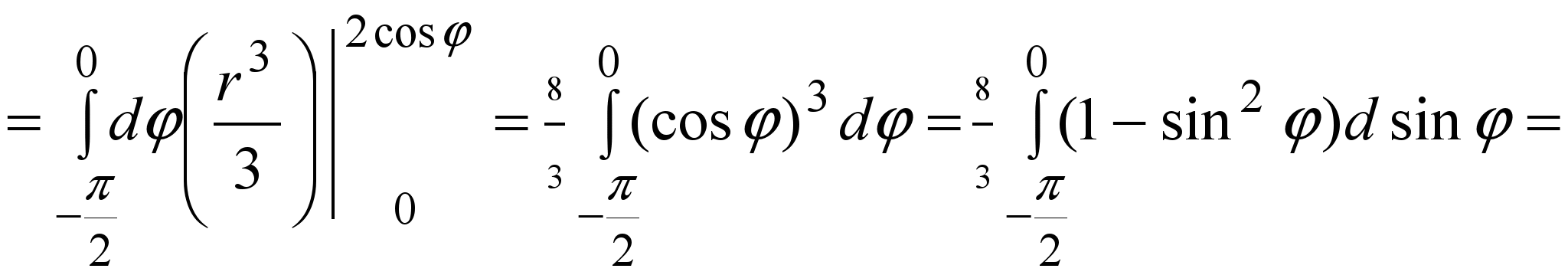
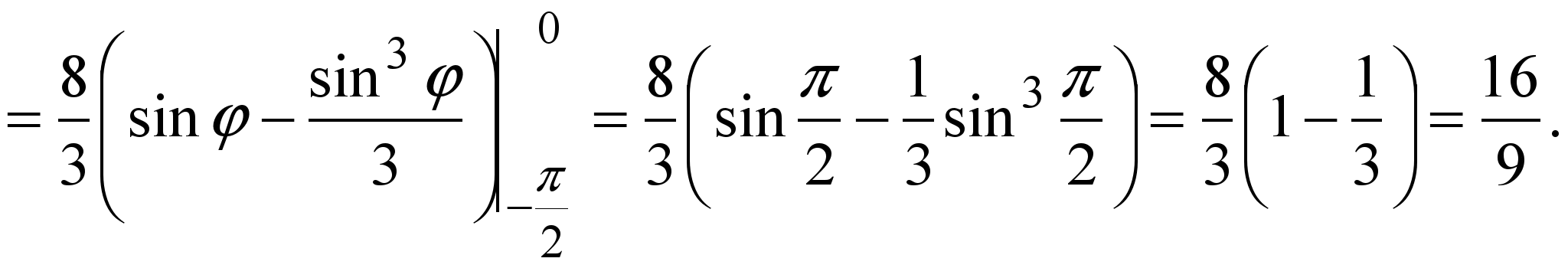
Вычисление площади фигуры.
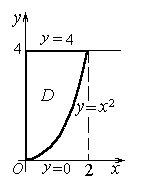
Площадь плоской фигуры вычисляется по формуле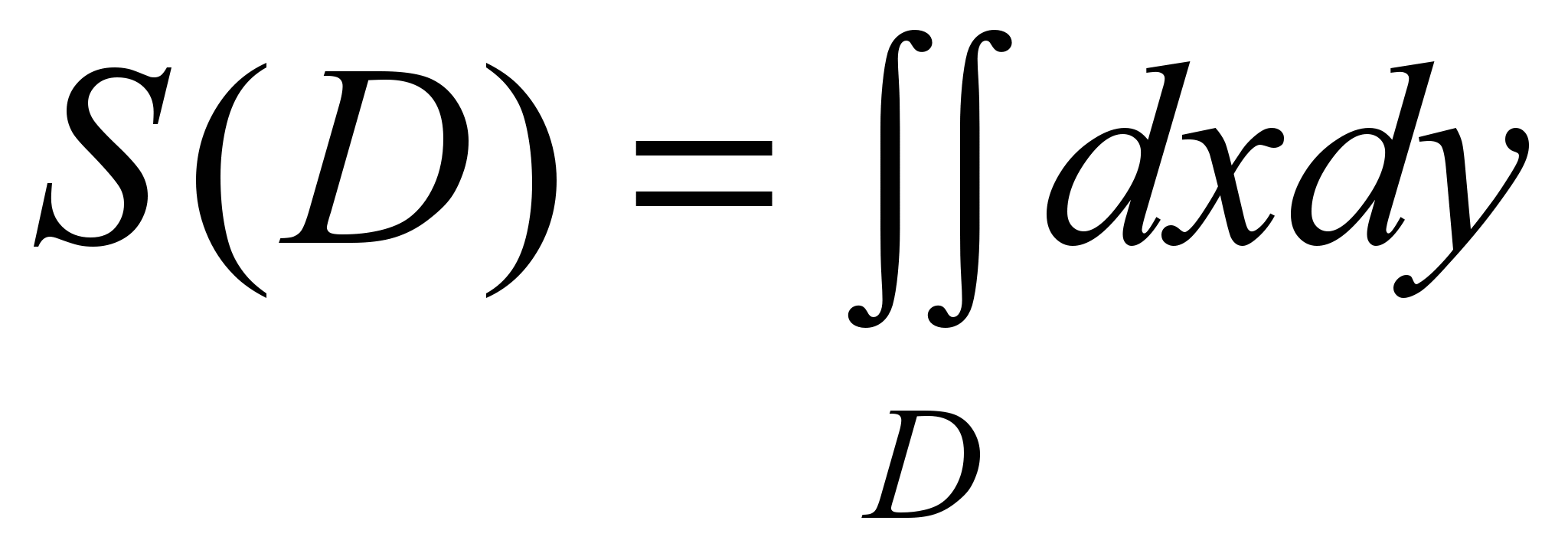
Пример. Вычислить площадь фигуры, ограниченной линиями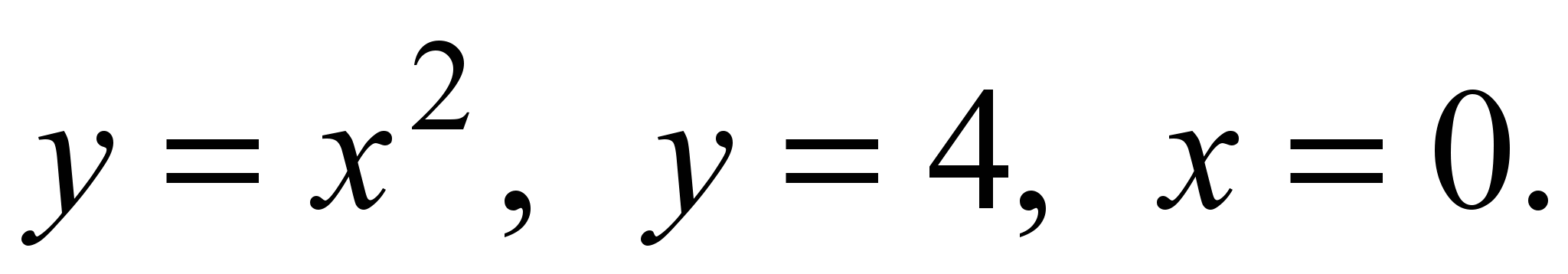
Решение. Данная фигура D расположена в вертикальной полосе 0 ≤ x ≤ 2, а в ней ограничена снизу параболой y = x2, сверху прямой y =4 (рис. 6). По формуле (5) имеем
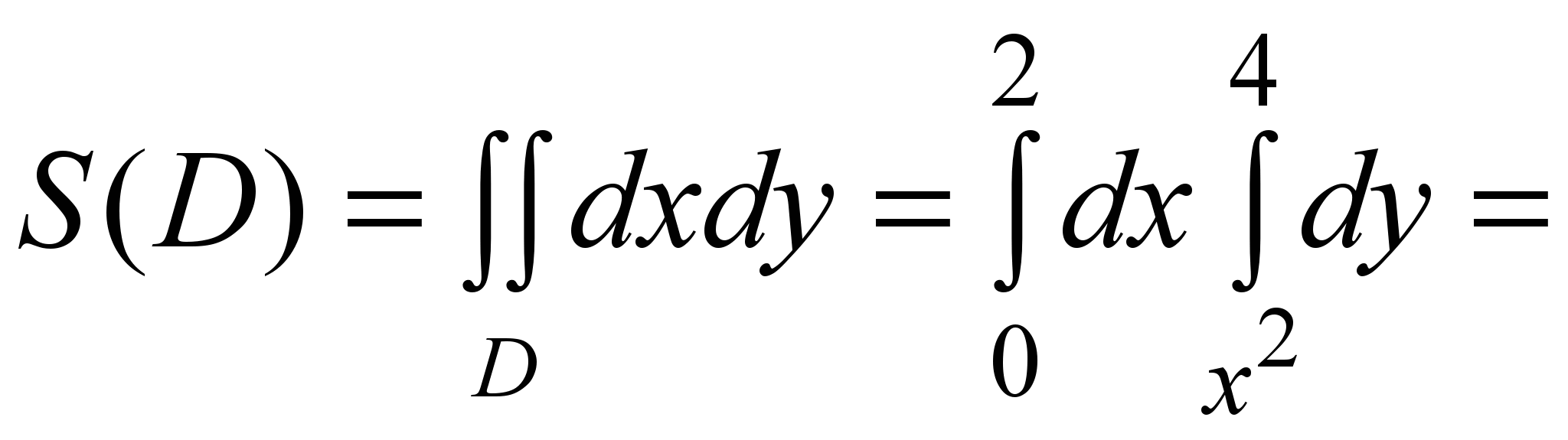
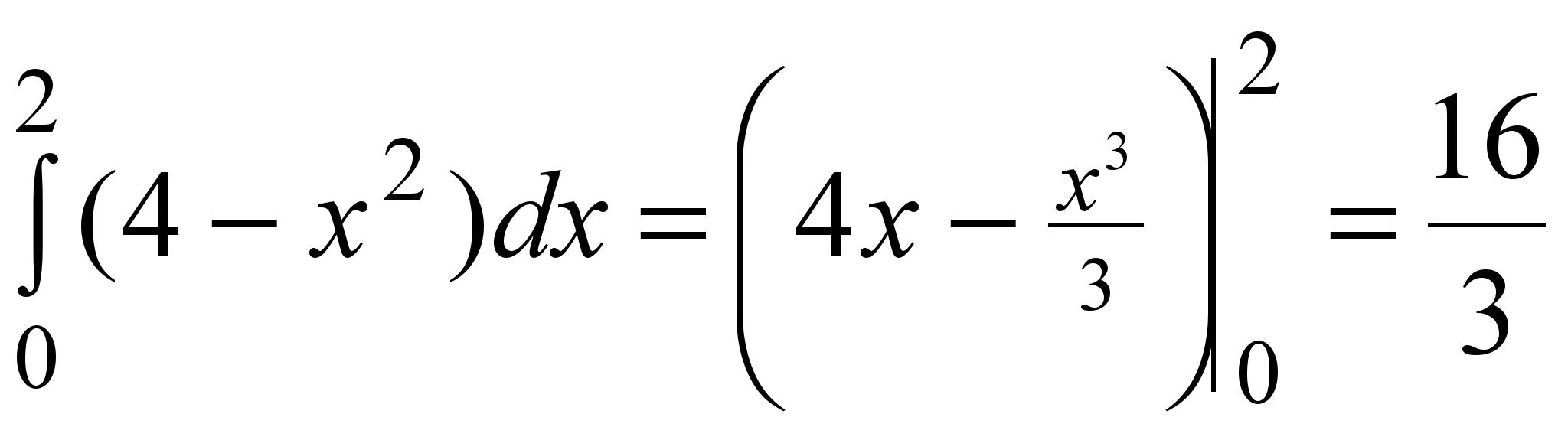 .
.
Вычисление объема цилиндрического тела.
Если f (x,y) ≥ 0 в ограниченной области D, то объем цилиндрического тела (рис.1) вычисляется по формуле V =
Пример. Найти объем тела, ограниченного поверхностями
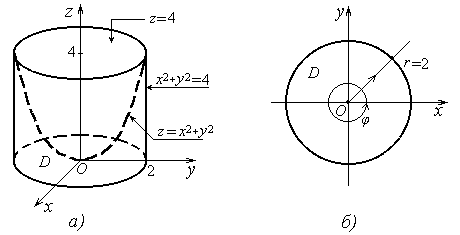
z = 0, x2 + y2 = 4, z = x2 + y2 .
Решение. x2 + y2 = 4 это круговой цилиндр радиуса 2, ось которого совпадает с Оy. z = x2 + y2 параболоид, который пересекает цилиндр по окружности радиуса 2 в плоскости z = 4 . z=0 координатная плоскость xOy. Таким образом, тело ограничено сверху параболоидом
z = x2 + y2 , снизу кругом D , с боков цилиндрической поверхностью x2 + y2 = 4. Так как данное тело цилиндрическое и
z = x2 + y2 ≥ 0, то для вычисления его объема можно использовать формулу
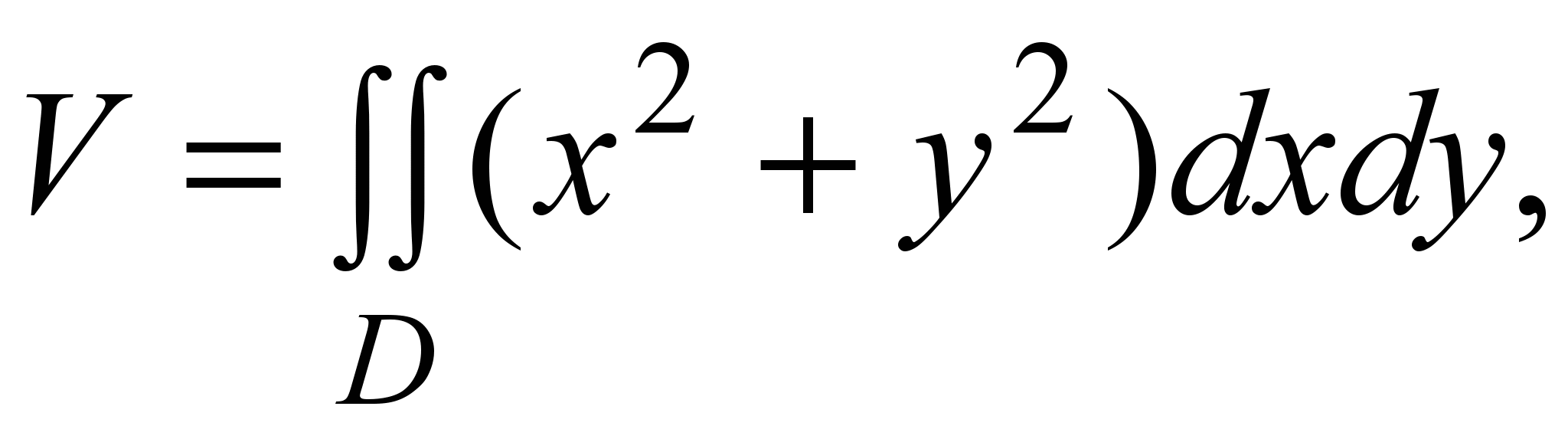
где D ={ (x, y) : x2 + y2 ≤ 4, z = 0}круг в плоскости xOy. Для вычисления этого интеграла перейдем к полярным координатам. При этом круг Dпреобразуется во множество
Dr ={ (r, φ) : 0 ≤ φ < 2π , 0 ≤ r ≤ 2 }. По формуле (17) получим
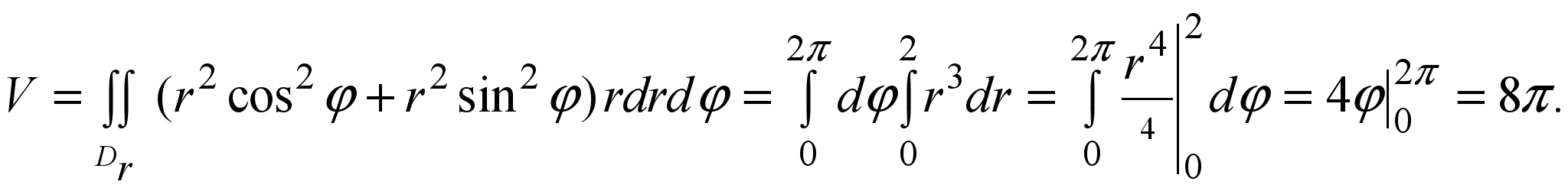

Занятие 27. Тема «Двойной интеграл и его свойства. Приложение двойного интеграла»
План лекции:
Понятие двойного интеграла
Определение: Двойной интеграл представляет собой обобщение понятия определенного интеграла на случай функции двух переменных. В этом случае вместо отрезка интегрирования будет присутствовать какая-то плоская фигура.
Двойной интеграл в общем виде записывается следующим образом:
, где – знак двойного интеграла;
D – область интегрирования (плоская фигура);
f(x;y) – подынтегральная функция двух переменных;
dx, dy – элементы площади интегрирования.
Пусть D – некоторая замкнутая ограниченная область, а f(x,y) – произвольная функция, определенная и ограниченная в этой области. Будем предполагать, что границы области D состоят из конечного числа кривых, заданных уравнениями вида y=f(x) или x=g(y), где f(x) и g(y) – непрерывные функции.
Свойства двойного интеграла
Правила вычисления двойного интеграла
Для такой области интеграл вычисляется следующим образом
Для такой области интеграл вычисляется следующим образом
Затем, вычисляется внешний интеграл также по формуле Ньютона-Лейбница.
Пример1. Вычислить двойной интеграл , где
Решение. 1. Строим область интегрирования D
2 . Находим границы области, то есть пределы интегрирования 1xy
3. Выбираем вид области интегрирования .
Вычисляем внутренний (правый) интеграл, считая у - числом, которое можно вынести за знак интеграла. Получаем .
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Пример 2. Вычислить двойной интеграл ,
где .
Решение. 1. Строим область интегрирования D
2. Находим границы области, то есть пределы интегрирования 1xy
3. Выбираем вид области интегрирования
Вычисляем внутренний (правый) интеграл, считая х - число. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Ответить на контрольные вопросы:
Тройной интеграл.
Контрольные вопросы.
Пусть функция u = f(x,y,z) определена в ограниченной замкнутой области V пространства R3. Разобьём область V произвольным образом наn элементарных замкнутых областей
Пусть декартовая полуось
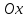 совпадает с полярным лучом .Декартовые координаты выражаются через полярные по формулам
совпадает с полярным лучом .Декартовые координаты выражаются через полярные по формулам 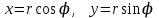 .
.Полярные координаты выражаются через декартовые
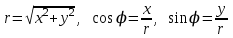 .
.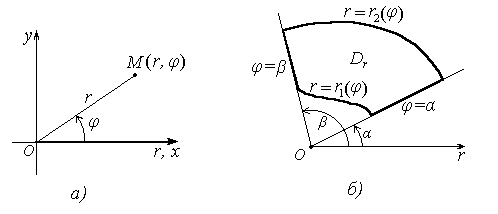
Пусть область D в декартовых координатах преобразуется в область Dr в полярных координатах согласно формулам (10).
Якобиан в данном случае равен:
Тогда интеграл (2) преобразуется в двойной интеграл в полярных координатах по формуле
Двойной интеграл (16) вычисляется переходом к повторному интегралу в полярных координатах. Пусть область Dr имеет вид
Dr= { (r, φ) : α ≤φ≤ β, r1(φ)≤ r≤ r2 (φ)},
где лучи φ= α и φ= β ограничивают сектор, в котором находится фигура Dr , кривые r = r1(φ), r = r2 (φ) ограничивают ее в этом секторе. Тогда
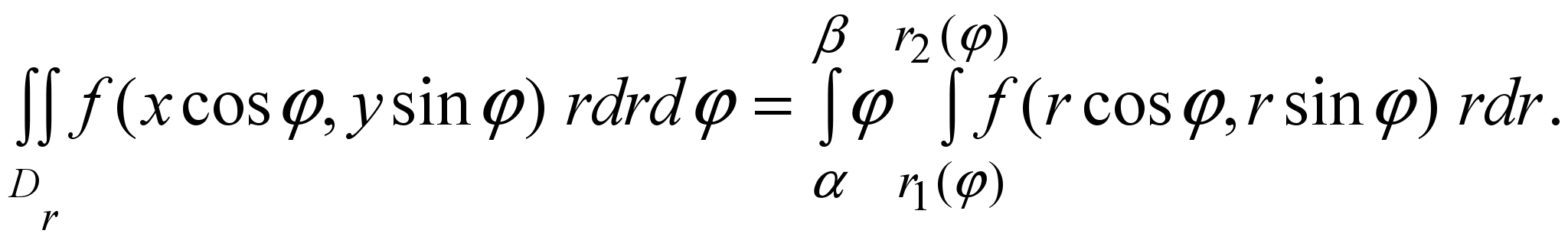 (17)
(17)Замечание. При расстановке пределов интегрирования в повторном интеграле нужно учесть, что изменение полярного угла определяется поворотом луча, исходящего из начала O вокруг него против хода часовой стрелки, а изменение полярного радиуса определяется движением точки вдоль луча в сторону его возрастания.

Рисунок 5
Примеры. 1). Расставить пределы интегрирования в повторном интеграле в полярных координатах
где Dr полукруг из рисунка 5.
Решение. Все точки этого полукруга будут охвачены, если луч Оl будет поворачиваться от
0 ≤ r ≤ 2cos φ. Таким образом, Dr ={(r, φ):
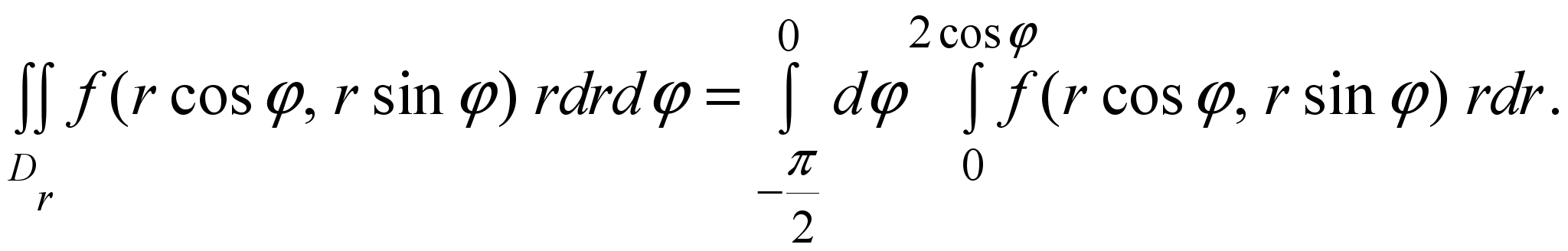
2) Вычислить
Решение. Подставим в уравнение окружности x2+y22x =0 полярные координаты (9) и преобразуем: r22 rcosφ= 0
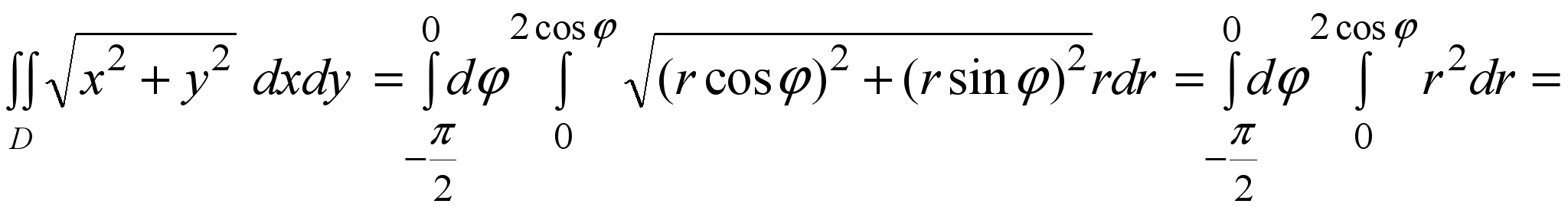
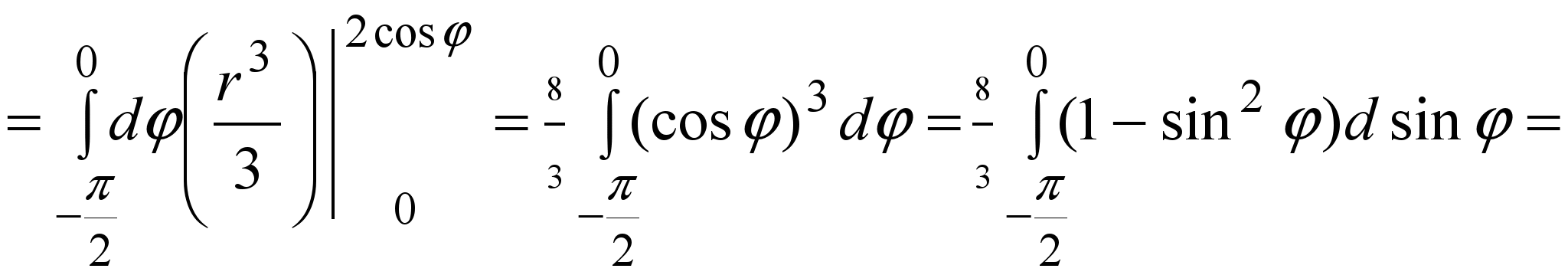
Вычисление площади фигуры.
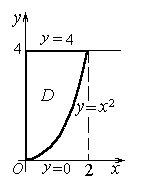
Площадь плоской фигуры вычисляется по формуле
Пример. Вычислить площадь фигуры, ограниченной линиями
Решение. Данная фигура D расположена в вертикальной полосе 0 ≤ x ≤ 2, а в ней ограничена снизу параболой y = x2, сверху прямой y =4 (рис. 6). По формуле (5) имеем
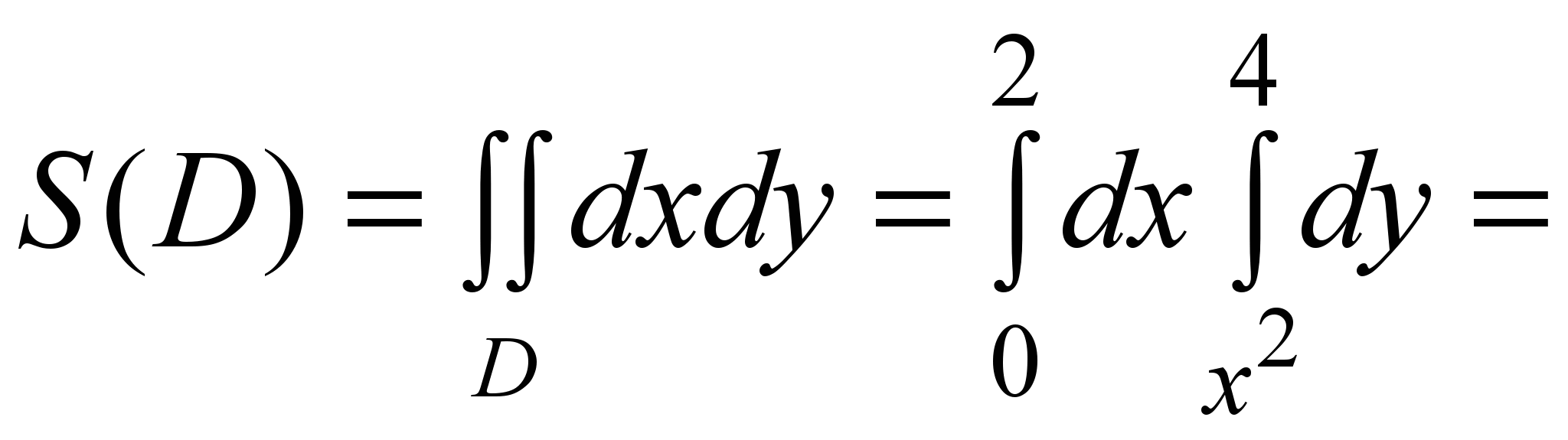
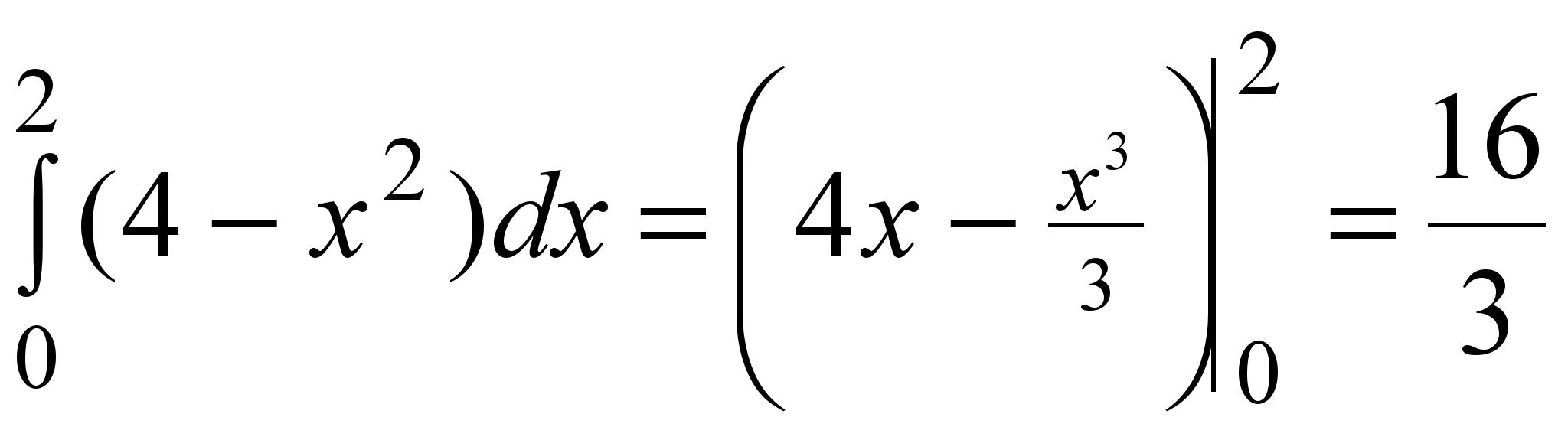 .
.Вычисление объема цилиндрического тела.
Если f (x,y) ≥ 0 в ограниченной области D, то объем цилиндрического тела (рис.1) вычисляется по формуле V =
Пример. Найти объем тела, ограниченного поверхностями
z = 0, x2 + y2 = 4, z = x2 + y2 .
Решение. x2 + y2 = 4 это круговой цилиндр радиуса 2, ось которого совпадает с Оy. z = x2 + y2 параболоид, который пересекает цилиндр по окружности радиуса 2 в плоскости z = 4 . z=0 координатная плоскость xOy. Таким образом, тело ограничено сверху параболоидом
z = x2 + y2 , снизу кругом D , с боков цилиндрической поверхностью x2 + y2 = 4. Так как данное тело цилиндрическое и
z = x2 + y2 ≥ 0, то для вычисления его объема можно использовать формулу
где D ={ (x, y) : x2 + y2 ≤ 4, z = 0}круг в плоскости xOy. Для вычисления этого интеграла перейдем к полярным координатам. При этом круг Dпреобразуется во множество
Dr ={ (r, φ) : 0 ≤ φ < 2π , 0 ≤ r ≤ 2 }. По формуле (17) получим

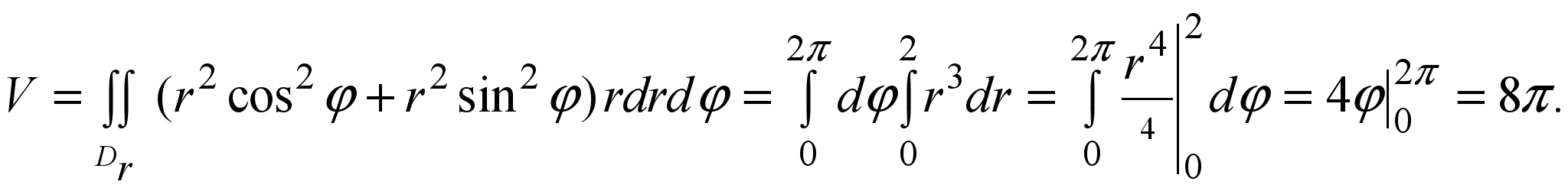
Занятие 27. Тема «Двойной интеграл и его свойства. Приложение двойного интеграла»
План лекции:
-
Понятие двойного интеграла -
Свойства двойного интеграла -
Правила вычисления двойного интеграла
Понятие двойного интеграла
Определение: Двойной интеграл представляет собой обобщение понятия определенного интеграла на случай функции двух переменных. В этом случае вместо отрезка интегрирования будет присутствовать какая-то плоская фигура.
Двойной интеграл в общем виде записывается следующим образом:
, где – знак двойного интеграла;
D – область интегрирования (плоская фигура);
f(x;y) – подынтегральная функция двух переменных;
dx, dy – элементы площади интегрирования.
Пусть D – некоторая замкнутая ограниченная область, а f(x,y) – произвольная функция, определенная и ограниченная в этой области. Будем предполагать, что границы области D состоят из конечного числа кривых, заданных уравнениями вида y=f(x) или x=g(y), где f(x) и g(y) – непрерывные функции.
Свойства двойного интеграла
-
Если С – числовая константа, то , -
-
Если область D “разбита” на области D1 и D2, то -
.
Правила вычисления двойного интеграла
-
Чтобы вычислить двойной интеграл, нужно для начала построить область D в системе координат и определить границы этой области по оси Ох и по оси Оу. Затем выбрать один из видов области интегрирования по правилу 2, подставить в функцию и вычислить двойной интеграл по 3 правилу. -
Различают два основных вида области интегрирования.
-
Область интегрирования D ограничена слева и справа прямыми х=а и х=b (ab), а снизу и сверху – непрерывными кривыми y= и y= ( ).
Для такой области интеграл вычисляется следующим образом
-
Область интегрирования D ограничена снизу и сверху прямыми у=с и y=d (cd), а слева и справа – непрерывными кривыми x= и y= ( )
Для такой области интеграл вычисляется следующим образом
-
При вычислении двойного интеграла сначала вычисляется внутренний интеграл, используя формулу Ньютона-Лейбница, считая одну из переменных постоянным числом:
-
здесь х считается постоянным числом. -
здесь у считается постоянным числом.
Затем, вычисляется внешний интеграл также по формуле Ньютона-Лейбница.
Пример1. Вычислить двойной интеграл , где
Решение. 1. Строим область интегрирования D
2 . Находим границы области, то есть пределы интегрирования 1xy
3. Выбираем вид области интегрирования .
Вычисляем внутренний (правый) интеграл, считая у - числом, которое можно вынести за знак интеграла. Получаем .
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Пример 2. Вычислить двойной интеграл ,
где .
Решение. 1. Строим область интегрирования D
2. Находим границы области, то есть пределы интегрирования 1xy
3. Выбираем вид области интегрирования
Вычисляем внутренний (правый) интеграл, считая х - число. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Ответить на контрольные вопросы:
-
Что называется двойным интегралом? -
Перечислите основные свойства двойного интеграла. -
На какие виды делится область интегрирования? -
Каким образом вычисляется двойной интеграл? -
Что делать с переменной, если она в интеграле не является интегрируемой? -
Пользуясь учебником П.Е. Данко «Высшая математика в упражнениях и задачах» часть 2, разобрать №4 стр.8 рис.3, выписать в тетрадь.
Тройной интеграл.
Контрольные вопросы.
-
Тройной интеграл, его свойства. -
Вычисление тройного интеграла в декартовых координатах. -
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах. -
Вычисление тройного интеграла в сферических координатах.
Пусть функция u = f(x,y,z) определена в ограниченной замкнутой области V пространства R3. Разобьём область V произвольным образом наn элементарных замкнутых областей

