листьев, желудей веток и корней.

Согласно второму способу, обход области будет следующим:


Таким образом:

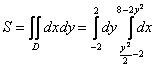
Как говорится, ощутите разницу.

1) Расправляемся с внутренним интегралом:


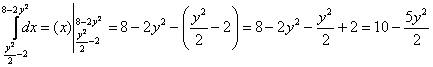
Результат подставляем во внешний интеграл:

2)


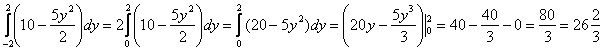
Интегрирование по переменной «игрек» не должно смущать, была бы буква «зю» – замечательно бы проинтегрировалось и по ней. Хотя кто прочитал второй параграф урока Как вычислить объем тела вращения, тот уже не испытывает ни малейшей неловкости с интегрированием по «игрек».

Также обратите внимание на первый шаг: подынтегральная функция  является чётной, а отрезок интегрирования симметричен относительно нуля. Поэтому отрезок можно споловинить, а результат – удвоить. Данный приём подробно закомментирован на уроке Эффективные методы вычисления определённого интеграла.

Что добавить…. Всё!

Ответ:

Для проверки своей техники интегрирования можете попробовать вычислить . Ответ должен получиться точно таким же.

интеграл.

Контрольные вопросы.

1. Двойной интеграл, его геометрический и физический смысл

2. Свойства двойного интеграла.

3. Вычисление двойного интеграла в декартовых координатах.

4. Замена переменных в двойном интеграле. Вычисление двойного интеграла в полярных координатах.

 

Замечание. Ниже будем считать все рассматриваемые кривые кусочно-гладкими. Диаметром замкнутой ограниченной области будем называть наибольшее из расстояний между двумя точками границы этой области
Пусть функция z= f(x,y) определена в ограниченной замкнутой области D плоскости. Разобьём область D произвольным образом на n элементарных замкнутых областей ₁, … ,_n, имеющих площади ₁, …,_n

---

 и диаметры d₁ , …, d_nсоответственно. Обозначим d наибольший из диаметров областей ₁, … ,_n . В каждой области _k выберем произвольную точку P_k (x_k ,y_k) и составим интегральную сумму функции f(x,y)

S =   (1)

Определение. Двойным интегралом функции f(x,y) по области D называется предел интегральной суммы

, (2)

если он существует.

Замечание. Интегральная суммаS зависит от способа разбиения области D и выбора точек P_k (k=1, …, n). Однако, предел  , если он существует, не зависит от способа разбиения области D и выбора точек P_k .

Достаточное условие существования двойного интеграла. Двойной интеграл (1) существует, если функция f(x,y)непрерывна в D за исключением конечного числа кусочно-гладких кривых и ограничена в D. В дальнейшем будем считать, что все рассматриваемые двойные интегралы существуют.
Геометрический смысл двойного интеграла.

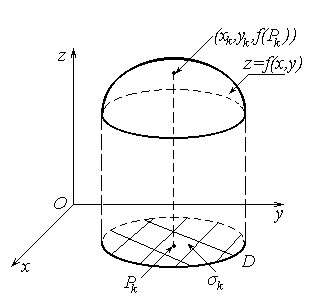
Если f(x,y)≥0 в области D, то двойной интеграл (1) равен объему «цилиндрического” тела, изображенного на рисунке:

V =  (3)

Цилиндрическое тело ограничено снизу областью D, сверху  частью поверхности z=f(x,y), с боков  вертикальными отрезками прямых, соединяющих границы этой поверхности и области D.
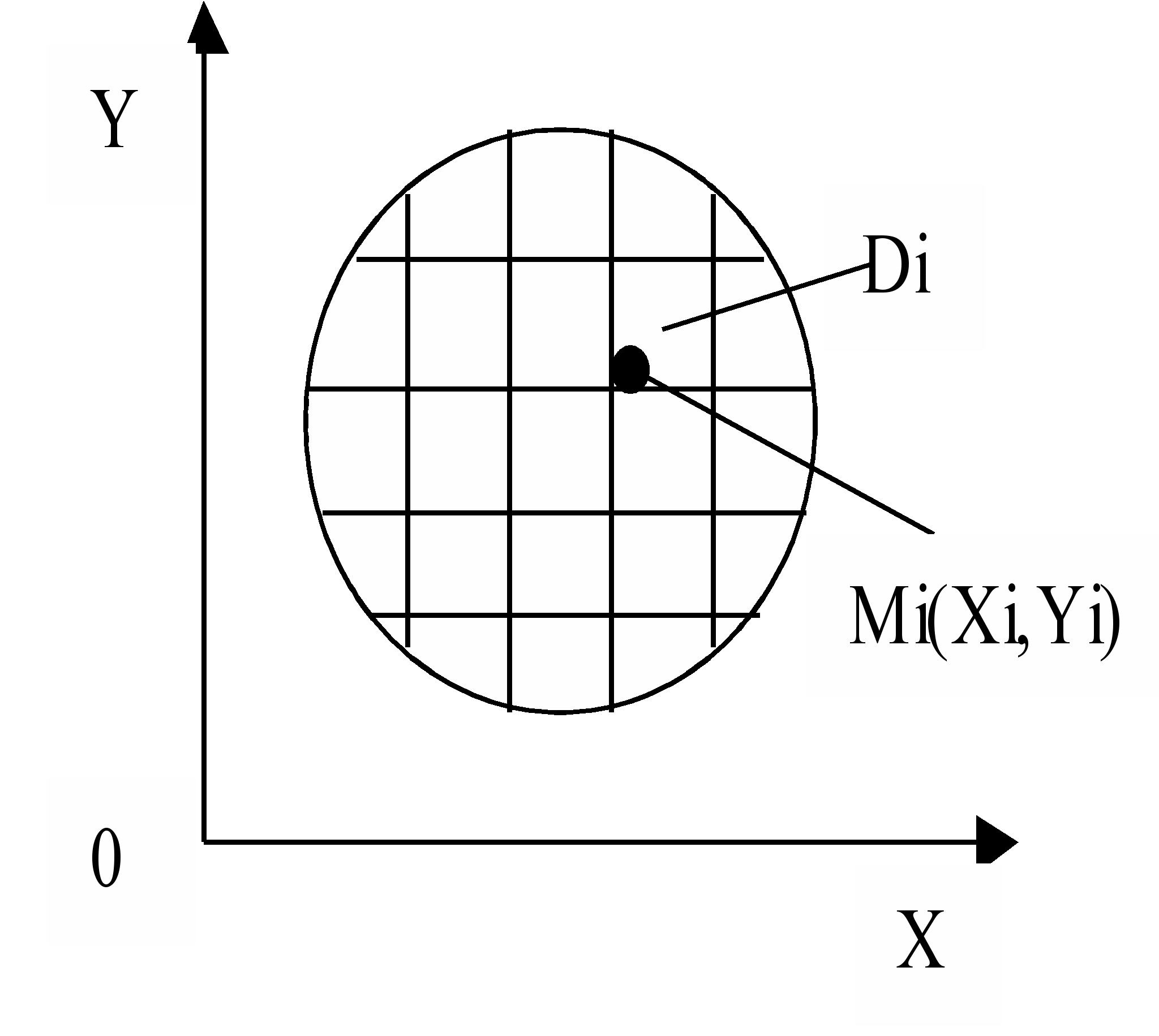
Физический смысл двойного интеграла. Масса плоской пластины.

Пусть задана плоская пластина D с известной функцией плотности γ(х,у), тогда разбивая пластину D на части D_i и выбирая произвольные точки  , получим для массы пластины  , или, сравнивая с формулой (2):

---

(4)
4. Некоторые свойства двойного интеграла.

1. 
   Линейность. Если С – числовая константа, то
   

,

2. 
   Аддитивность. Если область D «разбита” на области D₁и D₂, то
   

.

3) Площадь ограниченной области D равна

 (5)
Вычисление двойного интеграла в декартовых координатах.

---

Пусть задана область

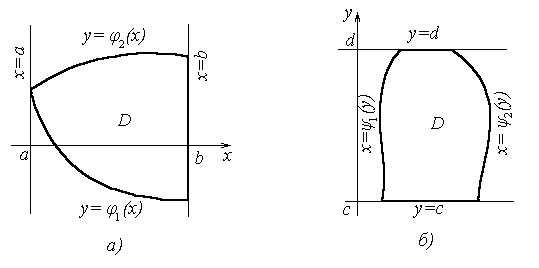
Рисунок 1
D ={(x, y): a ≤ x ≤ b, φ₁(x)≤ y≤ φ₂(x)} (6)

 
Область Dзаключена в полосе между прямыми x = a, y = b, снизу и сверху ограничена соответственно кривыми y = φ₁(x) и y = φ₂(x) .

Двойной интеграл (1) по области D (4) вычисляется переходом к повторному интегралу:

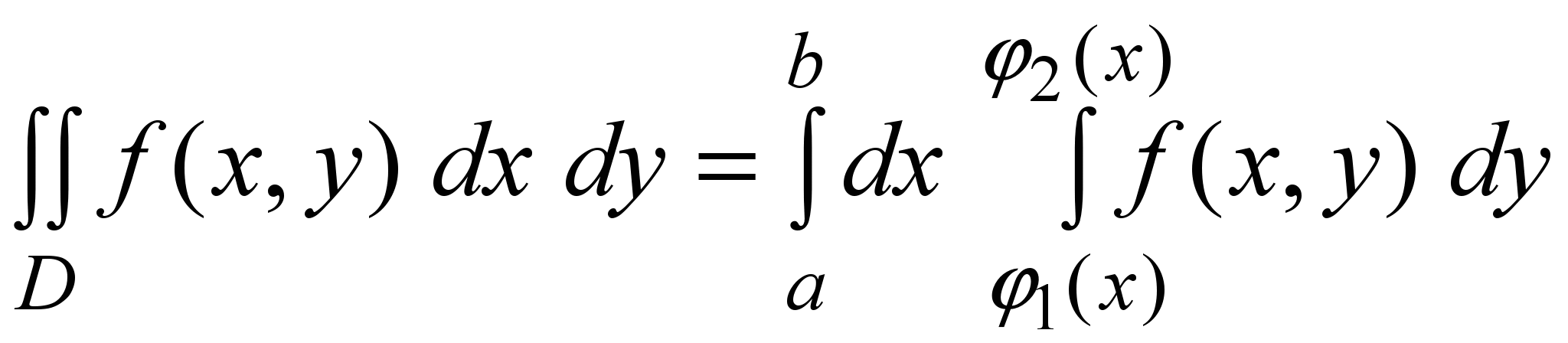 (7)

Этот повторный интеграл вычисляется следующим образом. Сначала вычисляется внутренний интеграл



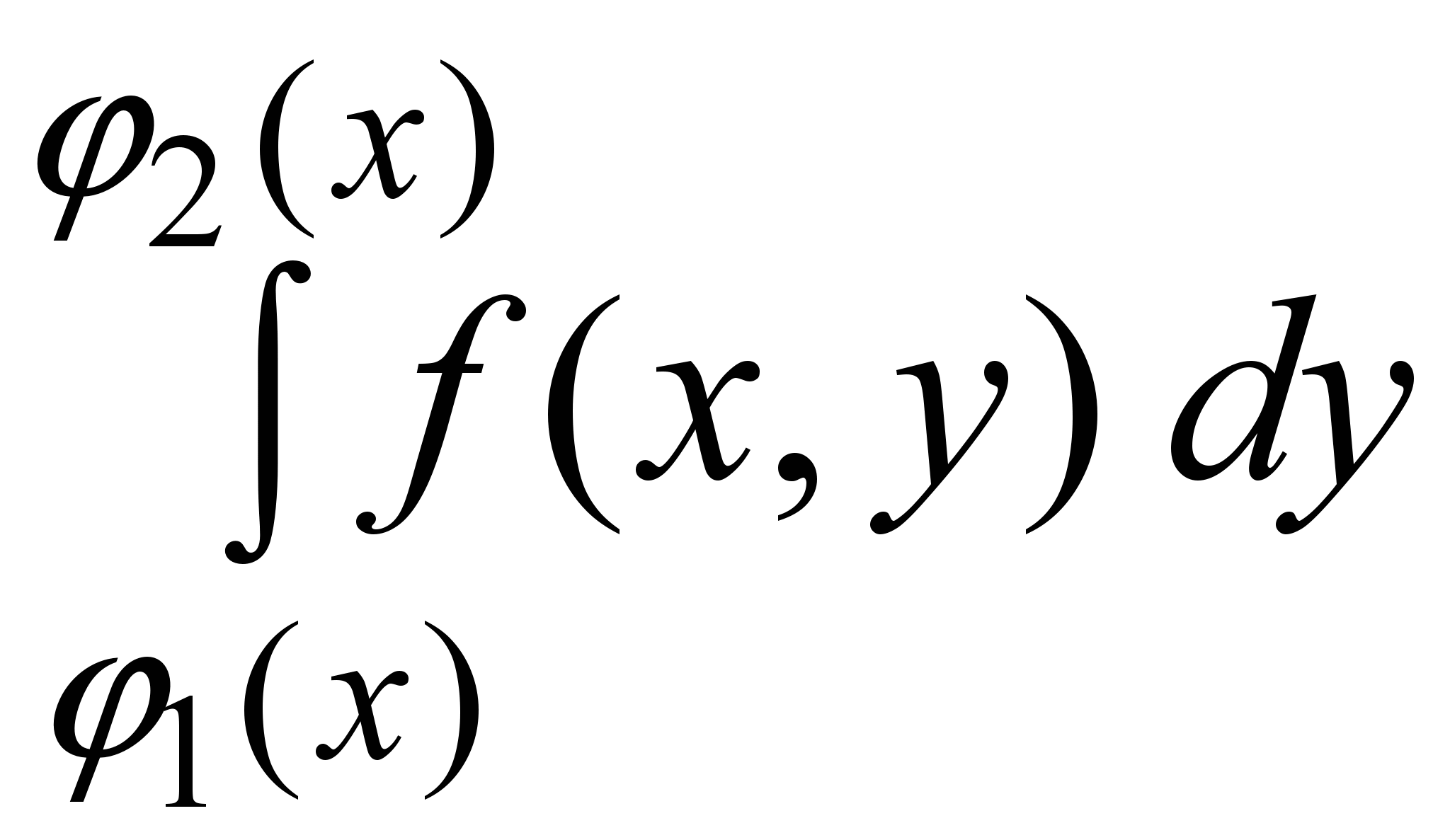
по переменной y, при этом x считается постоянной. В результате получится функция от переменной x, а затем вычисляется «внешний” интеграл от этой функции по переменной x.

Замечание. Процесс перехода к повторному интегралу по формуле (7) часто называют расстановкой пределов интегрирования в двойном интеграле. При расстановке пределов интегрирования нужно помнить два момента. Во-первых, нижний предел интегрирования не должен превышать верхнего, во-вторых, пределы внешнего интеграла должны быть константами, а внутреннего должны в общем случае зависеть от переменной интегрирования внешнего интеграла.

Пусть теперь область D имеет вид

D ={ (x, y) : c ≤ y ≤ d, ψ₁(y)≤ x ≤ ψ₂(y)} . (8)

Тогда

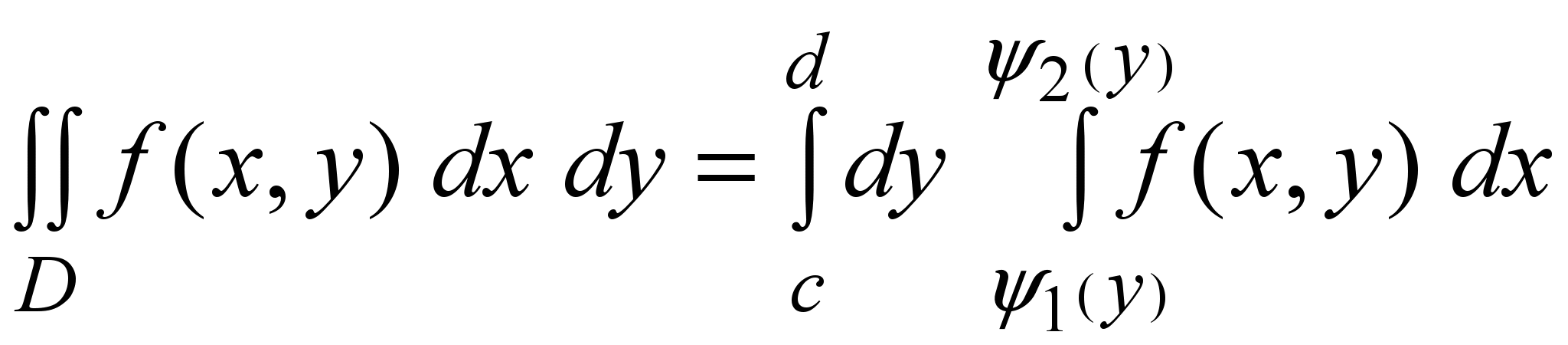. (9)

Предположим, что область D можно представить в виде (6) и (8) одновременно. Тогда имеет место равенство

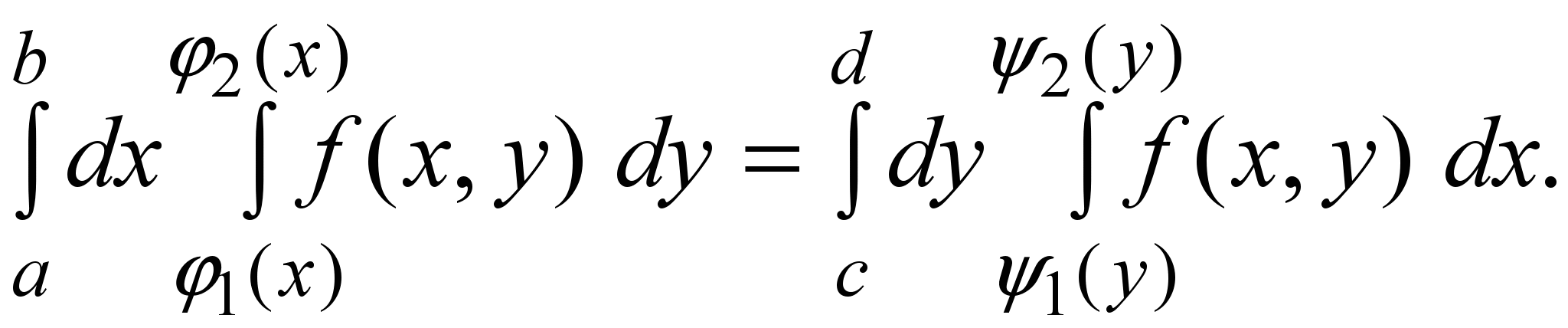(10)

Переход од одного повторного интеграла к другому в равенстве (10) называется изменением порядка интегрирования в двойном интеграле.


 

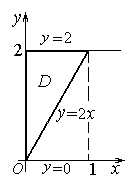
Примеры.

1) Изменить порядок интегрирования в интеграле

---

Решение. По виду повторного интеграла находим область

D ={(x, y): 0≤ x ≤1, 2x ≤ y≤2} .

Изобразим область D. По рисунку видим, что эта область расположена в горизонтальной полосе между прямыми y=0, y=2 и между линиями x =0и x = y  2. Это значит, что

D ={(x, y): 0≤ y ≤2, 0≤ x≤ y/2} .

Тогда по формуле (10) получаем

2)Вычислить интеграл   где D  область из примера 1.

Решение. Расставим пределы интегрирования в интеграле подобно примеру 1:



Вычислим внутренний интеграл по переменной y, считая x константой:



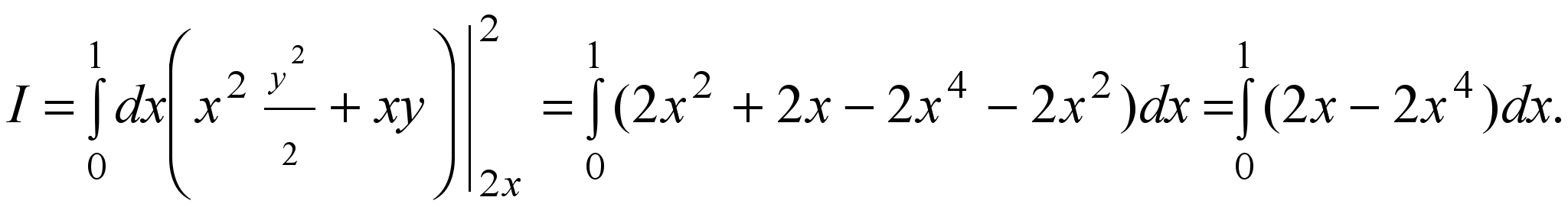
Теперь вычислим внешний интеграл по x:


Замена переменных в двойном интеграле.

Иногда для упрощения вычислений делают замену переменных:

,   (11)

Если функции (11) непрерывно дифференцируемы и определитель (Якобиан) отличен от нуля в рассматриваемой области:

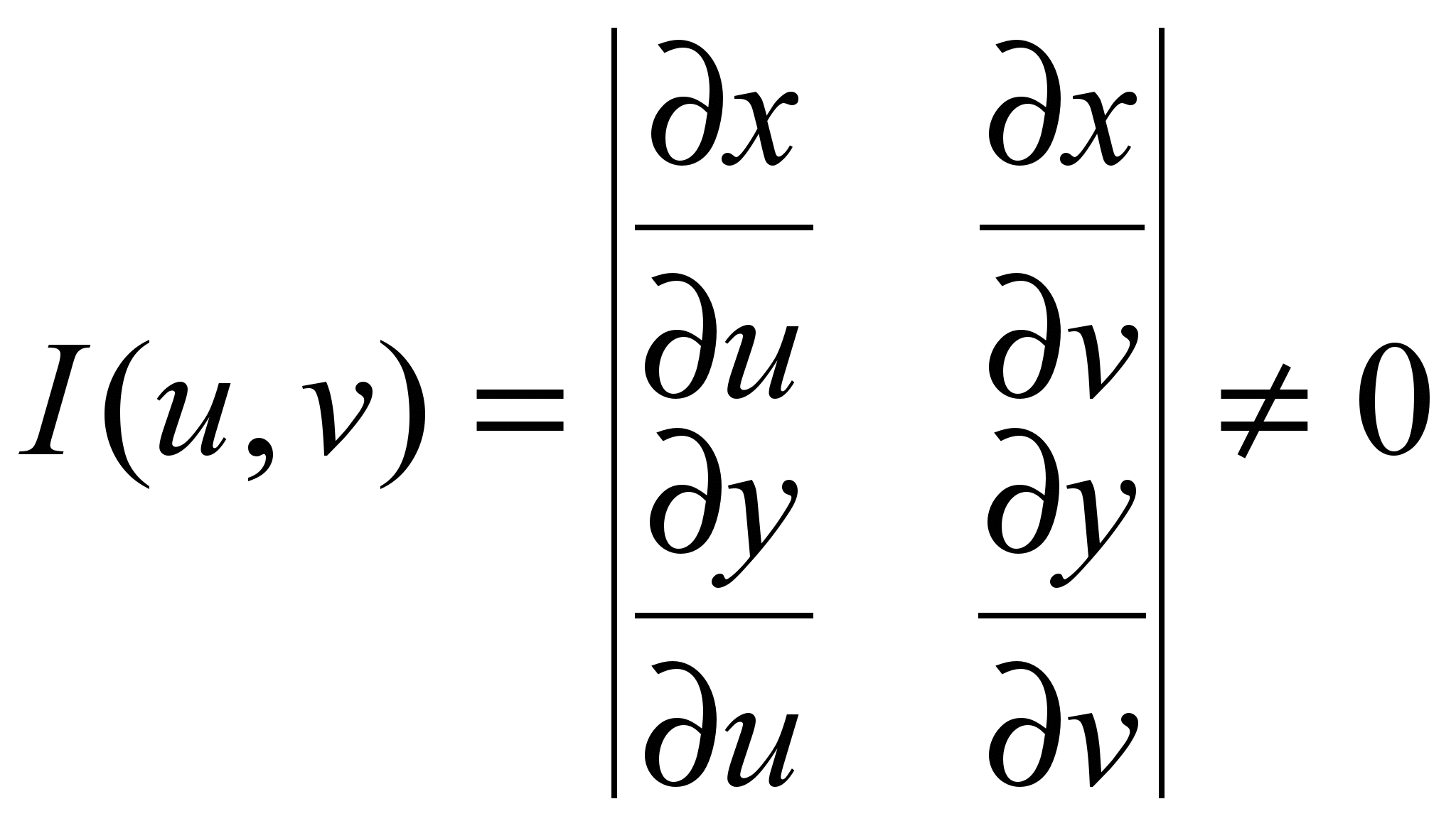 (12)

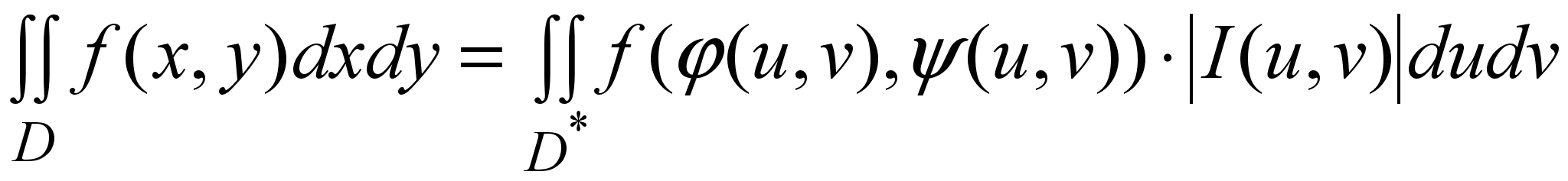то:   (13)

Двойной интеграл в полярных координатах

В полярных координатах точка 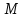однозначно определяется полярным углом 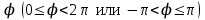и полярным радиусом 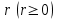. Для начала координат 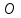радиус

---

Смотрите также файлы

• Лабораторная работа 5 Компоновка низа буровой колонны. Цель работы изучение элементов кнбк.docx

• Кормление собак.docx

• Видеофрагмент из фильма Тренер Картер.docx

• 2 Основные направления развития экономики Китайской Народной Республики25.docx

• Таырыбы Темекіні, насыбайды жне энергетикалы сусындарды зияны.docx