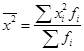Рис. 19. Основные показатели вариации
Размах вариации – это разность между наибольшим (x_max) и наименьшим (x_min) значениями вариантов.
R = x_max - x_min                           (33)

 

Пример 1. Определим показатель размаха вариации по данным табл. 27.

 

Таблица 27.

 

Группы предприятий по объему товарооборота

 

Товарооборот, млн. руб.	Число предприятий fi
90-100	28
100-110	48
110-120	20
120-130	4
ИТОГО	100

R = 130 - 90 = 40 млн. руб.
Размах показывает, что товарооборот предприятий изменяется (колеблется) в пределах от 90 до 130 млн руб., а общая ширина диапазона принимаемых значений (амплитуда колебаний) составляет 40 млн руб.

Размах измеряется в тех же абсолютных единицах, что и значения признака. Размах устанавливает ширину интервала, занимаемого значениями данных, но не отражает отклонений всех вариантов признака в ряду. Поскольку размах зависит только от крайних значений, его величина в большей мере подвержена воздействию случайности, так как в совокупности аномально большие или маленькие значения данных могут быть получены под влиянием случайных причин.

Чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение , которое учитывает различие всех единиц изучаемой совокупности.
Среднее линейное отклонение показывает стандартное отличие значения каждого варианта от общей средней величины и определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета их знака (по модулю):

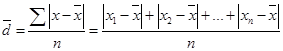                  (34)

Необходимость использования модуля связана со свойством средней арифметической (см. тему 5), согласно которому сумма индивидуальных отклонений от средней арифметической всегда равна нулю. Среднее линейное отклонение измеряется в тех же абсолютных единицах, что и значения признака.

---

 

Порядок расчета среднего линейного отклонения:

1)       по значениям признака находят среднюю арифметическую;

2)       определяют отклонения каждого значения x_i от средней ;

3)       рассчитывается сумма абсолютных величин отклонений: ;
4)       сумма абсолютных величин отклонений делится на число значений.
Пример 2. Рассчитаем среднее линейное отклонение стажа работников одной смены по данным табл. 28.

 

Таблица 28.

 

Стаж работников I смены бригады рабочих на предприятии

 

Таб. номер рабочего	Стаж работы, лет ( )
А	1	2	3
3 440	2	- 8	8
3 537	3	- 7	7
3 825	12	2	2
2 171	15	5	5
2 845	18	8	8
Итого	50	0	30

 

Средний стаж работы на одного рабочего смены составляет 10 лет (50 : 5 = 10). Отклонения стажа каждого рабочего от среднего стажа, равного 10 годам, рассчитаны в графе 2, их сумма равна нулю.

Среднее линейное отклонение составляет:
,
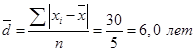т.е. стаж работы каждого работника данной смены в среднем отличается от их среднего значения на 6 лет.
Если данные наблюдения представлены в виде дискретного или интервального ряда распределения с частотами,  исчисляется по формуле средней арифметической взвешенной:

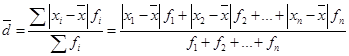              (35)

Порядок расчета взвешенного среднего линейного отклонения:

1)       вычисляется средняя арифметическая взвешенная;

2)       определяются абсолютные отклонения вариантов от средней ;

3)       полученные отклонения умножаются на частоты

---

;

4)       находится сумма взвешенных отклонений без учета знака: ;

5)       сумма взвешенных отклонений делится на сумму частот: .
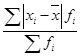Для нахождения  по интервальному ряду распределения вначале находят середины каждого интервала (как среднюю арифметическую из значений границ) и используют их для расчета отклонений от общей средней аналогичным образом.
Пример 3. Рассчитаем среднее линейное отклонение по данным о производительности труда работников одной смены по данным таблицы 29.

 

Таблица 29.

 

---

Производительность труда работников I смены бригады рабочих на предприятии

 

Количество деталей, обрабатываемых 1 рабочим, шт.	Количество рабочих, чел. fi	xi	xi fi (гр.3 * гр.2)		(гр.5*гр.2)
1	2	3	4	5	6
40 - 44	2	42	84	5	10
45 - 49	1	47	47	0	0
50 - 54	2	52	104	5	10
Итого	5	-	235	-	20

Для нахождения средней арифметической вначале были рассчитаны середины каждого интервала и записаны в графу 3. Эти значения показывают, сколько в среднем деталей обрабатывает за смену один работник по каждой группе производительности труда. Данные значения мы обозначаем как Х_i и будем использовать для дальнейших расчетов.

Средняя производительность труда одного рабочего данной смены составляет 235 : 5 = 47 деталей:

Индивидуальные отклонения от средней (без учета знака) указаны в графе 5. Взвешенные отклонения – в графе 6, их сумма составляет 20 единиц.

Следовательно: .
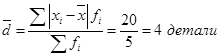Это значит, что в среднем каждый работник данной смены обрабатывает за рабочее время на 4 детали меньше или больше, чем средний уровень производительности по смене, составляющий 47 деталей.

Несмотря на то, что среднее линейное отклонение учитывает колеблемость всех значений признака, при его расчете в некотором смысле нарушается элементарное правило математики, так как отклонения от среднего значения суммируются без учета знаков.

Избежать указанного недочета позволяет возведение каждого индивидуального отклонения от средней в квадрат. Рассчитав среднюю величину из возведенных в квадрат отклонений, можно вернуться к исходному порядку данных путем извлечения квадратного корня. Найденное число будет также характеризовать типичное отклонение вариантов признака от средней величины в данной совокупности.

---

На практике квадратические оценки признаются более состоятельными, поскольку они не нарушают математических правил, а размер погрешности от возведения в квадрат является минимальным. Это объясняется вторым свойством средней арифметической величины (см. тему 5), согласно которому сумма квадратов отклонений от средней всегда меньше, чем аналогичная величина, рассчитанная от любого другого числа.

Основными показателями вариации, для расчета которых используются квадратические оценки, являются дисперсия и среднее квадратическое отклонение.
Дисперсия – это средняя арифметическая из квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается . В зависимости от исходных данных дисперсия может вычисляться как средняя арифметическая простая или взвешенная.
Если каждый вариант признака повторяется только один раз, используют простую (невзвешенную) формулу:

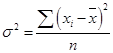               (36)

Если варианты признака повторяются неодинаковое количество раз, используют взвешенную формулу:

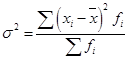            (37)

Среднее квадратическое отклонение (в литературе также часто используется термин «стандартное отклонение») представляет собой квадратный корень из дисперсии и обозначается .

Формулы для его расчета следующие:

·     среднее квадратическое отклонение невзвешенное:

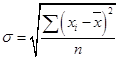             (38)

·     среднее квадратическое отклонение взвешенное:

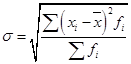           (39)

Математические преобразования формул (38) и (39) приводят к упрощенному виду формулы, которая часто оказывается более удобной на практике, особенно при расчете s по несгруппированным данным:

,                (40)

где

---

Смотрите также файлы

• Классный частренинг Мотивация учения.pdf

• 2. Письменно ответьте на вопросы Понятие об антропогенном кризисе и катастрофе.doc

• Решение Определим фондоотдачу (фотд) Фотд 42000 16000 2,625 тыс руб.docx

• Методические указания по выполнению лабораторной работы по дисциплине Теплофизика для студентов направления 20. 03. 01 Техносферная безопасность.pdf

• Фгбоу во ниу мэи.docx