ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 193
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(41)
Среднее квадратическое отклонение является обобщающей характеристикой абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.) и показывает, насколько в среднем отличается значение каждого варианта признака от среднего значения для данной совокупности.
Среднее квадратическое отклонение всегда больше среднего линейного отклонения. Между ними имеется соотношение:
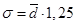 (42)
(42)
Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.
Для вычисления среднего квадратического отклонения необходимо рассчитать дисперсию.
Порядок расчета дисперсии по взвешенной формуле:
1) определяют среднюю арифметическую взвешенную;
2) рассчитывают отклонения вариантов от средней: ;
3) возводят в квадрат отклонение каждого варианта от средней: ;
;
4) умножают квадраты отклонений на веса (частоты):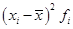 ;
;
5) суммируют полученные произведения: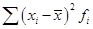 ;
;
6) полученную сумму делят на сумму весов: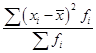 .
.
Пример 4. Найдем дисперсию и среднее квадратическое отклонение по данным о размере квартальной премии сотрудников одного из отдела фирмы (табл. 30).
Таблица 30.
Размер квартальной премии сотрудников отдела обслуживания фирмы
Исчислим среднюю арифметическую взвешенную:
500 : 50 = 10 тыс. руб.
Значения отклонений от средней и их квадратов представлены в таблице 30 в графах 4 и 5.
Определим дисперсию: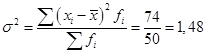 .
.
Среднее квадратическое отклонение будет равно:
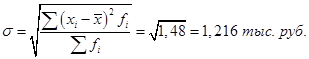
Это значит, что размер премии каждого сотрудника отдела обслуживания отличается от среднеквартальной величины премии по отделу, равной 10 тыс. руб., на 1 216 руб.
Если исходные данные представлены в виде интервального ряда распределения, то сначала надо определить средины каждого интервала, и далее рассчитывать показатели вариации аналогичным образом.
Пример 5. Рассчитаем дисперсию и среднее квадратическое отклонение по данным о распределении ценных бумаг по уровню доходности (табл. 31).
Таблица 31.
Распределение ценных бумаг по уровню доходности, %
Средняя доходность одной ценной бумаги равна:
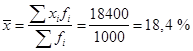
Исчислим дисперсию: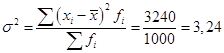 .
.
Среднее квадратическое отклонение составит: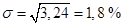 .
.
Следовательно, с каждой ценной бумаги владелец может получить в среднем на 1,8 % больше или меньше, чем величина средней доходности – 18,4 %.
Для характеристики меры вариации изучаемого признака исчисляются показатели в относительных величинах. Они позволяют сравнивать характер вариации признака в разных совокупностях. Относительные показатели вариации рассчитывают как отношение типичного отклонения к средней величине, умножаемое на 100 %.
Линейный коэффициент вариации характеризует долю среднего линейного отклонения от общего размера средней величины и рассчитывается по формуле:
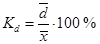 (43)
(43)
Коэффициент вариации рассчитывается как отношение среднего квадратического отклонения к средней величине:
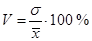 (44)
(44)
Учитывая, что среднеквадратическое отклонение дает обобщающую характеристику колеблемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем, используемым для оценки типичности средних величин. Если V больше 40 %, то это говорит о большой колеблемости признака в изучаемой совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33,3 %.
Пример 6. По данным таблицы 31 рассчитаем коэффициент вариации.
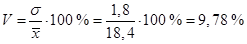
Это означает, что ценные бумаги однородны по проценту доходности (т.к. V = 9,78 % < 33 %).
Следует отметить, что коэффициент вариации может быть более 100 %, что бывает при наличии значений, сильно отличающихся от средней величины, например, отрицательных значений или аномально больших или малых значений отдельных вариантов. Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине и для более качественного ее исследования необходимо разбить ее на более однородные части или с помощью специальных методов исключить влияние на среднюю аномальных вариантов.
Вопрос 3. Математические свойства показателей вариации.
На практике часто возникают ситуации, которые системно оказывают влияние на все значения исследуемого признака. Например, при системном сокращении или повышении расценок, переходе к использованию для расчетов условных единиц, переходе с одной валюты на другую (с доллара США к евро или фунтам стерлингов), при изменении шкалы измерений. Такие изменения отражаются в систематическом увеличении или уменьшении каждого значения показателя на некоторые фиксированные величины или в несколько раз. При таких изменениях необходимости в перерасчете всех показателей вариации не возникает, так как они обладают рядом математических свойств, зная которые, можно легко определить их величину по совокупности обновленных данных. Рассмотрим основные свойства на примере данных о затратах на производство единицы продукции трех отделений корпорации, каждое из которых в среднем ежемесячно производит 2 тыс. единиц продукции (табл. 32).
Таблица 32.
Затраты на производство единицы продукции по корпорации
Так как каждое отделение производит одинаковое количество продукции, для расчета обобщающих показателей – средней, дисперсии, среднего квадратического отклонения – можно воспользоваться невзвешенной формулой. Промежуточные расчеты показателей представлены в таблице 33.
Таблица 33.
Затраты на производство единицы продукции по корпорации
Средние затраты на единицу продукции корпорации составляют 12 руб. Риск превышения затрат на единицу продукции составляет 1,632 руб. – величину среднего квадратического отклонения. Общие производственные затраты в месяц составляют в среднем:
12 * 6000 = 72 000 руб.
Свойство 1. Уменьшение или увеличение всех значений признака на одинаковую величину не меняет величины дисперсии, среднего квадратического отклонения и размаха вариации.
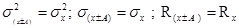 (45)
(45)
Проверим, как повлияет на величину показателей вариации снижение затрат на единицу продукции на 2 руб. в результате оптимизации производственных процессов при неизменном объеме производства (табл. 34).
Таблица 34.
Затраты на производство единицы продукции по корпорации
Среднее квадратическое отклонение является обобщающей характеристикой абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.) и показывает, насколько в среднем отличается значение каждого варианта признака от среднего значения для данной совокупности.
Среднее квадратическое отклонение всегда больше среднего линейного отклонения. Между ними имеется соотношение:
Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.
Для вычисления среднего квадратического отклонения необходимо рассчитать дисперсию.
Порядок расчета дисперсии по взвешенной формуле:
1) определяют среднюю арифметическую взвешенную;
2) рассчитывают отклонения вариантов от средней: ;
3) возводят в квадрат отклонение каждого варианта от средней:
4) умножают квадраты отклонений на веса (частоты):
5) суммируют полученные произведения:
6) полученную сумму делят на сумму весов:
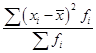 .
.Пример 4. Найдем дисперсию и среднее квадратическое отклонение по данным о размере квартальной премии сотрудников одного из отдела фирмы (табл. 30).
Таблица 30.
Размер квартальной премии сотрудников отдела обслуживания фирмы
| Премия, тыс. руб. (xi) | Число сотрудников, fi | xi fi | | | |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 8 | 7 | 56 | -2 | 4 | 28 |
| 9 | 10 | 90 | -1 | 1 | 10 |
| 10 | 15 | 150 | 0 | 0 | 0 |
| 11 | 12 | 132 | 1 | 1 | 12 |
| 12 | 6 | 72 | 2 | 4 | 24 |
| ИТОГО | 50 | 500 | 0 | - | 74 |
Исчислим среднюю арифметическую взвешенную:
500 : 50 = 10 тыс. руб.
Значения отклонений от средней и их квадратов представлены в таблице 30 в графах 4 и 5.
Определим дисперсию:
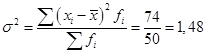 .
.Среднее квадратическое отклонение будет равно:
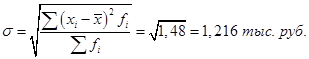
Это значит, что размер премии каждого сотрудника отдела обслуживания отличается от среднеквартальной величины премии по отделу, равной 10 тыс. руб., на 1 216 руб.
Если исходные данные представлены в виде интервального ряда распределения, то сначала надо определить средины каждого интервала, и далее рассчитывать показатели вариации аналогичным образом.
Пример 5. Рассчитаем дисперсию и среднее квадратическое отклонение по данным о распределении ценных бумаг по уровню доходности (табл. 31).
Таблица 31.
Распределение ценных бумаг по уровню доходности, %
| Доходность 1 ценной бумаги, % | Количество ценных бумаг, fi | xi | xifi | | | |
| 14–16 | 100 | 15 | 1500 | -3,4 | 11,56 | 1156 |
| 16–18 | 300 | 17 | 5100 | -1,4 | 1,96 | 588 |
| 18–20 | 400 | 19 | 7600 | 0,6 | 0,36 | 144 |
| 20–22 | 200 | 21 | 4200 | 2,6 | 6,76 | 1352 |
| ИТОГО | 1000 | - | 18400 | | | 3240 |
Средняя доходность одной ценной бумаги равна:
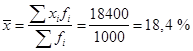
Исчислим дисперсию:
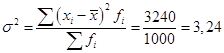 .
.Среднее квадратическое отклонение составит:
Следовательно, с каждой ценной бумаги владелец может получить в среднем на 1,8 % больше или меньше, чем величина средней доходности – 18,4 %.
Для характеристики меры вариации изучаемого признака исчисляются показатели в относительных величинах. Они позволяют сравнивать характер вариации признака в разных совокупностях. Относительные показатели вариации рассчитывают как отношение типичного отклонения к средней величине, умножаемое на 100 %.
Линейный коэффициент вариации характеризует долю среднего линейного отклонения от общего размера средней величины и рассчитывается по формуле:
Коэффициент вариации рассчитывается как отношение среднего квадратического отклонения к средней величине:
Учитывая, что среднеквадратическое отклонение дает обобщающую характеристику колеблемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем, используемым для оценки типичности средних величин. Если V больше 40 %, то это говорит о большой колеблемости признака в изучаемой совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33,3 %.
Пример 6. По данным таблицы 31 рассчитаем коэффициент вариации.
Это означает, что ценные бумаги однородны по проценту доходности (т.к. V = 9,78 % < 33 %).
Следует отметить, что коэффициент вариации может быть более 100 %, что бывает при наличии значений, сильно отличающихся от средней величины, например, отрицательных значений или аномально больших или малых значений отдельных вариантов. Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине и для более качественного ее исследования необходимо разбить ее на более однородные части или с помощью специальных методов исключить влияние на среднюю аномальных вариантов.
Вопрос 3. Математические свойства показателей вариации.
На практике часто возникают ситуации, которые системно оказывают влияние на все значения исследуемого признака. Например, при системном сокращении или повышении расценок, переходе к использованию для расчетов условных единиц, переходе с одной валюты на другую (с доллара США к евро или фунтам стерлингов), при изменении шкалы измерений. Такие изменения отражаются в систематическом увеличении или уменьшении каждого значения показателя на некоторые фиксированные величины или в несколько раз. При таких изменениях необходимости в перерасчете всех показателей вариации не возникает, так как они обладают рядом математических свойств, зная которые, можно легко определить их величину по совокупности обновленных данных. Рассмотрим основные свойства на примере данных о затратах на производство единицы продукции трех отделений корпорации, каждое из которых в среднем ежемесячно производит 2 тыс. единиц продукции (табл. 32).
Таблица 32.
Затраты на производство единицы продукции по корпорации
| Отделение корпорации | Затраты на единицу продукции, руб. (Хi) | Средний объем производства, единиц продукции в месяц |
| А | 1 | 2 |
| 1 отделение | 10 | 2 000 |
| 2 отделение | 12 | 2 000 |
| 3 отделение | 14 | 2 000 |
| Итого | - | 6 000 |
Так как каждое отделение производит одинаковое количество продукции, для расчета обобщающих показателей – средней, дисперсии, среднего квадратического отклонения – можно воспользоваться невзвешенной формулой. Промежуточные расчеты показателей представлены в таблице 33.
Таблица 33.
Затраты на производство единицы продукции по корпорации
| № отделения | Хi | | |
| А | 1 | 2 | 3 |
| 1 отделение | 10 | - 2 | 4 |
| 2 отделение | 12 | 0 | 0 |
| 3 отделение | 14 | + 2 | 4 |
| Итого | 36 | 0 | 8 |
| | |
| | |
| | |
Средние затраты на единицу продукции корпорации составляют 12 руб. Риск превышения затрат на единицу продукции составляет 1,632 руб. – величину среднего квадратического отклонения. Общие производственные затраты в месяц составляют в среднем:
12 * 6000 = 72 000 руб.
Свойство 1. Уменьшение или увеличение всех значений признака на одинаковую величину не меняет величины дисперсии, среднего квадратического отклонения и размаха вариации.
Проверим, как повлияет на величину показателей вариации снижение затрат на единицу продукции на 2 руб. в результате оптимизации производственных процессов при неизменном объеме производства (табл. 34).
Таблица 34.
Затраты на производство единицы продукции по корпорации
| № отделения | (Хi- 2) | (Хi - 2) - | ((Хi - 2) - )2 |
| А | 1 | 2 | 3 |
| 1 | 8 | - 2 | 4 |
| 2 | 10 | 0 | 0 |
| 3 | 12 | + 2 | 4 |
| Итого | 30 | 0 | 8 |
| | |
| | |

